水塔流量估计数学建模.docx

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.12M 资料格式：docx 举报版权申诉

Justin137794613-2536188-4744302543349321186.docx.pdf-第1页.png

第1页 / 共11页

Justin137794613-2536188-4744302543349321186.docx.pdf-第2页.png

第2页 / 共11页

Justin137794613-2536188-4744302543349321186.docx.pdf-第3页.png

第3页 / 共11页

Justin137794613-2536188-4744302543349321186.docx.pdf-第4页.png

第4页 / 共11页

Justin137794613-2536188-4744302543349321186.docx.pdf-第5页.png

第5页 / 共11页

Justin137794613-2536188-4744302543349321186.docx.pdf-第6页.png

第6页 / 共11页

Justin137794613-2536188-4744302543349321186.docx.pdf-第7页.png

第7页 / 共11页

Justin137794613-2536188-4744302543349321186.docx.pdf-第8页.png

第8页 / 共11页

前言

1问题提出

2问题分析

3模型假设

3.1忽略水位对流速的影响

3.2供水时段的假设

3.3单位时间的供水量为常数

3.4流量是对时间的连续函数

3.5流量与水泵是否工作无关

3.6流量定义的假设

4流量估计

4.1拟合水位—时间函数

4.2确定流量—时间函数

4.3一天总用水量的估计

5算法设计与编程

5.1 拟合第1、2时段的水位，并到处流量

5.1.1第1时段的流速：

5.1.2第2时段的流速

5.2拟合供水时段的流量

5.3一天的总用水量的估计

5.4流量及总用水量的检验

6计算结果

7分析与改进

总结

参考文献

附录Ⅰ部分源代码

《数学模型与数学软件综合训练》论文训练题目：水塔流量估计学生学号：07500119 姓名：周才祥计通院信息与计算科学专业指导教师：黄灿云（理学院） 2010 年春季学期

目录前言............................................................................................................................................................. 2 摘要................................................................................................................................................................. 3 关键词............................................................................................................................................................... 3 1 问题提出 ........................................................................................................................................................4 2 问题分析 ........................................................................................................................................................4 3 模型假设 ........................................................................................................................................................4 3.1 忽略水位对流速的影响 .....................................................................................................................4 3.2 供水时段的假设.................................................................................................................................5 3.3 单位时间的供水量为常数.................................................................................................................5 3.4 流量是对时间的连续函数.................................................................................................................5 3.5 流量与水泵是否工作无关.................................................................................................................5 3.6 流量定义的假设.................................................................................................................................5 4 流量估计 ........................................................................................................................................................5 4.1 拟合水位—时间函数.........................................................................................................................5 4.2 确定流量—时间函数.........................................................................................................................6 4.3 一天总用水量的估计.........................................................................................................................6 5 算法设计与编程 ............................................................................................................................................6 5.1 拟合第 1、2 时段的水位，并到处流量......................................................................................... 6 5.1.1 第 1 时段的流速： ..................................................................................................................6 5.1.2 第 2 时段的流速 ......................................................................................................................7 5.2 拟合供水时段的流量.........................................................................................................................7 5.3 一天的总用水量的估计 .....................................................................................................................7 5.4 流量及总用水量的检验 .....................................................................................................................8 6 计算结果 ........................................................................................................................................................8 7 分析与改进 ....................................................................................................................................................8 总结 ................................................................................................................................................................... 9 参考文献 ...........................................................................................................................................................9 附录Ⅰ部分源代码 .........................................................................................................................................10 1 07500119 周才祥 10 年春数学模型与数学软件综合训练

前言在生产实践和科学研究中，常常遇到这样的问题：由实验或测量得到的一批离散样点，需要确定满足特定要求的曲线或曲面（即变量之间的函数关系或预测样点之外的数据）。如果要求曲线（面）通过所给的所有数据点（即确定一个初等函数通过已知各数据，一般用多项式或分段多项式），这就是数据插值。在数据较少的情况下，这样做能够取得好的效果。但是，如果数据较多，那么插值函数是一个次数很高的函数，比较复杂。如果不要求曲线（面）通过所有的数据点，而是要求它反映对象整体的变化趋势，可得到更简单实用的近似函数，这就是数据拟合。函数插值和曲线拟合都是要根据一组数据构造一个函数作为近似，由于近似的要求不同，二者在数学方法上是完全不同的。针对水塔数据分析，利用数学软件 MATLAB 进行数据拟合。曲线拟合问题是指：已知平面上 n 个点（ ix ， iy ），i ＝0，1，…，n ， ix 互不相同，寻求函数 y ＝ )(xf ，使 )(xf 在某种准则下与所有数据点最为接近，即曲线拟合得最好。线性最小二乘法是解决曲线拟合最常用的方法，其基本思路是，令 )(xf ＝ )(11 xra ＋ )(22 xra ＋…＋ ra mm )(x 其中 )(xrk 是事先选定的一组函数，系数 ka （ k ＝0，1，…，m , m < n ）待定。寻求 ka ，使得残差 n 平方和Q ＝ i 1  ( ( ixf )  2 i )y 达到最小。这里的建模原理实质上与实验七中的回归分析是一致的。 2 07500119 周才祥 10 年春数学模型与数学软件综合训练

摘要数学建模方法是处理科学理论的一种经典方法,也是解决各类实际问题的常用方法。文章采用曲线拟合的方法 ,并利用数学软件 MATLAB 对水塔流蚤进行计算计算结果与实际记录基本吻合。关键词：建模，流量，拟合，MATLAB 3 07500119 周才祥 10 年春数学模型与数学软件综合训练

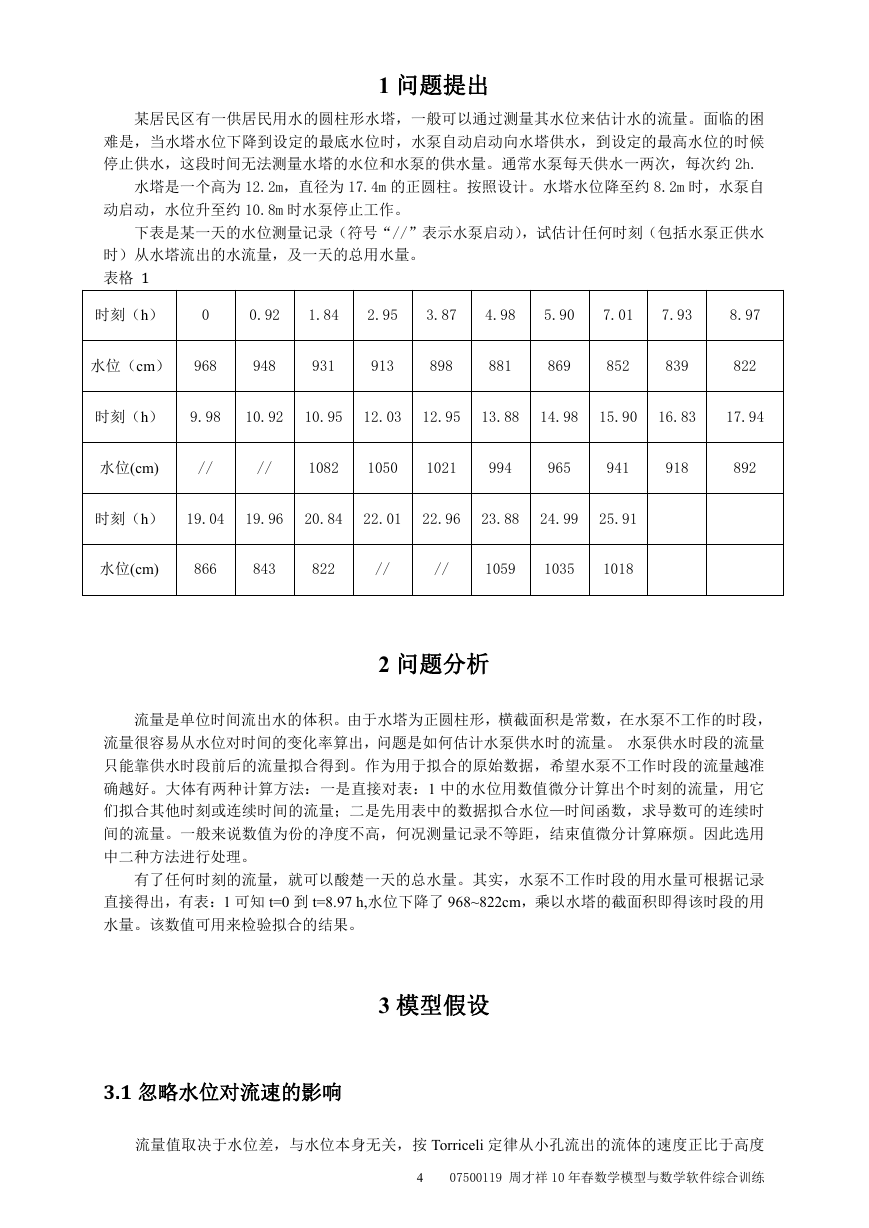
1 问题提出某居民区有一供居民用水的圆柱形水塔，一般可以通过测量其水位来估计水的流量。面临的困难是，当水塔水位下降到设定的最底水位时，水泵自动启动向水塔供水，到设定的最高水位的时候停止供水，这段时间无法测量水塔的水位和水泵的供水量。通常水泵每天供水一两次，每次约 2h. 水塔是一个高为 12.2m，直径为 17.4m 的正圆柱。按照设计。水塔水位降至约 8.2m 时，水泵自动启动，水位升至约 10.8m 时水泵停止工作。下表是某一天的水位测量记录（符号“//”表示水泵启动），试估计任何时刻（包括水泵正供水时）从水塔流出的水流量，及一天的总用水量。表格1 时刻（h） 0 0.92 1.84 2.95 3.87 4.98 5.90 7.01 7.93 8.97 水位（cm） 968 948 931 913 898 881 869 852 839 822 时刻（h） 9.98 10.92 10.95 12.03 12.95 13.88 14.98 15.90 16.83 17.94 水位(cm) // // 1082 1050 1021 994 965 941 918 892 时刻（h） 19.04 19.96 20.84 22.01 22.96 23.88 24.99 25.91 水位(cm) 866 843 822 // // 1059 1035 1018 2 问题分析流量是单位时间流出水的体积。由于水塔为正圆柱形，横截面积是常数，在水泵不工作的时段，流量很容易从水位对时间的变化率算出，问题是如何估计水泵供水时的流量。水泵供水时段的流量只能靠供水时段前后的流量拟合得到。作为用于拟合的原始数据，希望水泵不工作时段的流量越准确越好。大体有两种计算方法：一是直接对表：1 中的水位用数值微分计算出个时刻的流量，用它们拟合其他时刻或连续时间的流量；二是先用表中的数据拟合水位—时间函数，求导数可的连续时间的流量。一般来说数值为份的净度不高，何况测量记录不等距，结束值微分计算麻烦。因此选用中二种方法进行处理。有了任何时刻的流量，就可以酸楚一天的总水量。其实，水泵不工作时段的用水量可根据记录直接得出，有表：1 可知 t=0 到 t=8.97 h,水位下降了 968~822cm，乘以水塔的截面积即得该时段的用水量。该数值可用来检验拟合的结果。 3 模型假设 3.1 忽略水位对流速的影响流量值取决于水位差，与水位本身无关，按 Torriceli 定律从小孔流出的流体的速度正比于高度 4 07500119 周才祥 10 年春数学模型与数学软件综合训练

的平方根，水塔的高度和最低水位为 10.8m、802m（设出水口的水位为 0），因 10.88.2=1.15≈1 故可忽略水位对流速的影响。 3.2 供水时段的假设水泵第一次供水时段为 t1=9h 到 t2 =11h，第二次供水时段为 t3=20.8h 到 t4=23h 这是根据最高和最低水位分别为 10.8m 和 8.2m，以及表 1 的水位测量纪录作出的假设，其中前 3 个时刻直接取自实测数据（精确到 0.1h），最后 1 个时刻来自每次供水约 2h 的已知条件（从记录上看，第 2 次供水时段应在有记录的 22.96h 之后即将结束）。 3.3 单位时间的供水量为常数水泵工作时单位时间的供水量基本为常数，这个厂书读与单位时间的平均流量。 3.4 流量是对时间的连续函数流量是单位时间流出水的体积，这里假设流量是对时间的连续函数。 3.5 流量与水泵是否工作无关为简化处理，不影响问题的解决，假设流量与水泵是工作无关。 3.6 流量定义的假设由于水塔截面积是常数π17.424 =237.8m2，为简单起见，在计算中将流量定义做单位时间流出的水的高度，即水位（水位时下降的）对时间变化率的绝对值，最后给出结果再乘以 S 即可。 4 流量估计 4.1 拟合水位—时间函数由表 1 记录，一天有两个供水时段（以下称第一个供水时段和第二个供水时段），和三个水泵不工作时段（以下称第 1 时段 t=0 到 t=8.97，第 2 个时段 t=10.95 到 t-20.84，和第 3 时段 t=23 以后）。对第 1、2 时段的测量数据直接分别做多项式函数拟合，得到水位函数。为使拟合曲线比较光滑，多项式次数不要太高，一把为 3~6 次。由于第 3 时段只有 3 个测量记录，无法对这一时段的水位作出较好的拟合。 5 07500119 周才祥 10 年春数学模型与数学软件综合训练

4.2 确定流量—时间函数对于第 1、2 时段只需将水位函数求导即可，对于两个供水时段的流量，则用供水时段前后（水泵不工作）的流量拟合得到，且将第 2 时段流量外推，将第 3 个时段流量包含在第 2 供水时段内。 4.3 一天总用水量的估计总用水量等于两个不工作时段和两个工作时段用水量之和，它们都可由流量对时间的积分得到。下面利用数学软件 MATLAB 对水塔流量进行计算与曲线拟合。 5 算法设计与编程 5.1 拟合第 1、2 时段的水位，并到处流量 5.1.1 第 1 时段的流速： *********************************实现代码************************************* t=[0,0.92,1.84,2.95,3.87,4.98,5.90,7.01,7.93,8.97,9.98,10.92,10.95,12.03,12.95,13.88,14.98,15.90,16.8 3,17.94,19.04,19.96,20.84,22.01,22.96,23.88,24.99,25.91]; 948 931 913 898 881 869 852 839 822 h=[968 965 941 918 892 866 843 822 0 0 1059 0 0 1035 1050 1082 1018];%水泵启动是水位用“0”表 1021 994 示 c1=polyfit(t(1:10),h(1:10),3);%用 3 次多项式拟合第 1 时段水位，c1 输出 3 次多项式的系数 a1=polyder(c1);%输出多项式（系数为 c1）导数的系数 tp1=0:0.1:9; x1=-polyval(a1,tp1); %x1 输出多项式（系数为 a1）在 tp1 点的函数值（取负后变为正值），即 tp1 时刻的流量，类似可计算第 2 时段各时刻的流量 ******************************************************************************* 6 07500119 周才祥 10 年春数学模型与数学软件综合训练

图5.1.1 5.1.2 第 2 时段的流速 *********************************实现代码************************************* c2=polyfit(t(1:10),h(1:10),3);%用 3 次多项式拟合第 1 时段水位，c2 输出 3 次多项式的系数 a2=polyder(c2);%输出多项式（系数为 c1）导数的系数 tp2=11:0.1:20; x2=-polyval(a2,tp2); %x2 输出多项式（系数为 a2）在 tp2 点的函数值（取负后变为正值），即 tp2 时刻的流量，类似可计算第 2 时段各时刻的流量 ******************************************************************************* 5.2 拟合供水时段的流量 5.2.1 在第一供水时段(t=9~11)之前（即第 1 时段）和之后（即第 2 时段）各取几点，其流量已经得到，用它们拟合第 1 供水时段的流量。为使流量函数在 t=9 和 t=11 连续，我们任意取 4 个点，拟合 3 次多项式，实现如下： *********************************实现代码************************************* 9]);%取第 1 时段在 t=8,9 的流量 xx1=-polyval(a1,[8 xx2=-polyval(a1,[11 12]);%取第 2 时段在 t=11,12 的流量 xx12=[xx1 c12=polyfit([8 tp12=9:0.1:11; x12=polyval(c12,tp12);%x12 输出第一供水时段各时刻的流量。 11 12],xx12,3);%拟合 3 次多项式 xx2]; 9 ******************************************************************************* 5.2.2 在第 2 供水时段之前取 t=20，20.8 两点的流量，在该时段之后（第 3 时段）仅有 3 个水位个水位记录，用差分得到流量，然后用这 4 个数值拟合第二供水时段的流量如下： *********************************实现代码************************************* dt3=diff(t(22:24));%最后 3 个时刻的两两之差 dh3=diff(h(22:24));%最后 3 个水位的两两之差 dth3=-dh3/dt3;%t（22）和 t（23）的流量 t3=[20,20.8,t(22),t(23)]; xx3=[-polyval(a2,t3(1:4),dth3)];%t3 各时刻的流量 c3=polyfit(t3,xx3,3);%拟合 3 次多项式 tp3=20.8:0.1:24; x3=polyval(c3,tp3)；%x 输出第二供水时段（外推至 t=24）各时刻的流量 ******************************************************************************* 5.3 一天的总用水量的估计第 1、2 时段和第一、二供水时段流量的积分之和，就是的总用水量。虽然诸时段流量已表示为多项式函数，积分可解析的算出，使用数值积分计算如下： *********************************实现代码************************************* y1=0.1*trapz(x1);%第 1 时段用水量（仍然以高度表示），0.1 为几分步长 y2=0.1*trapz(x2);%第 2 时段用水量 7 07500119 周才祥 10 年春数学模型与数学软件综合训练

分享到：

赞收藏

资料库

水塔流量估计数学建模.docx

相关推荐

开发技术

热门标签

最新资料