数据结构课程设计报告迷宫游戏.doc

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：0.14M 资料格式：doc 举报版权申诉

yk758204203-3110195-20090302149张宇豪.doc.pdf-第1页.png

第1页 / 共17页

yk758204203-3110195-20090302149张宇豪.doc.pdf-第2页.png

第2页 / 共17页

yk758204203-3110195-20090302149张宇豪.doc.pdf-第3页.png

第3页 / 共17页

yk758204203-3110195-20090302149张宇豪.doc.pdf-第4页.png

第4页 / 共17页

yk758204203-3110195-20090302149张宇豪.doc.pdf-第5页.png

第5页 / 共17页

yk758204203-3110195-20090302149张宇豪.doc.pdf-第6页.png

第6页 / 共17页

yk758204203-3110195-20090302149张宇豪.doc.pdf-第7页.png

第7页 / 共17页

yk758204203-3110195-20090302149张宇豪.doc.pdf-第8页.png

第8页 / 共17页

一、课程名称

二、课题设计的基本思想，原理和算法描述

三、源程序及注释

四、运行示例及结果分析

五、调试和运行程序过程中产生的问题及采取的措施

六、对课题相关算法的讨论、分析，改进设想

七、总结

八、参考文献

《数据结构》课程设计报告课题名称：__迷宫问题专业班级： 09 计本一学姓号： 20090302149 名：张宇豪指导老师：刘杰 2010 年 12 月 1

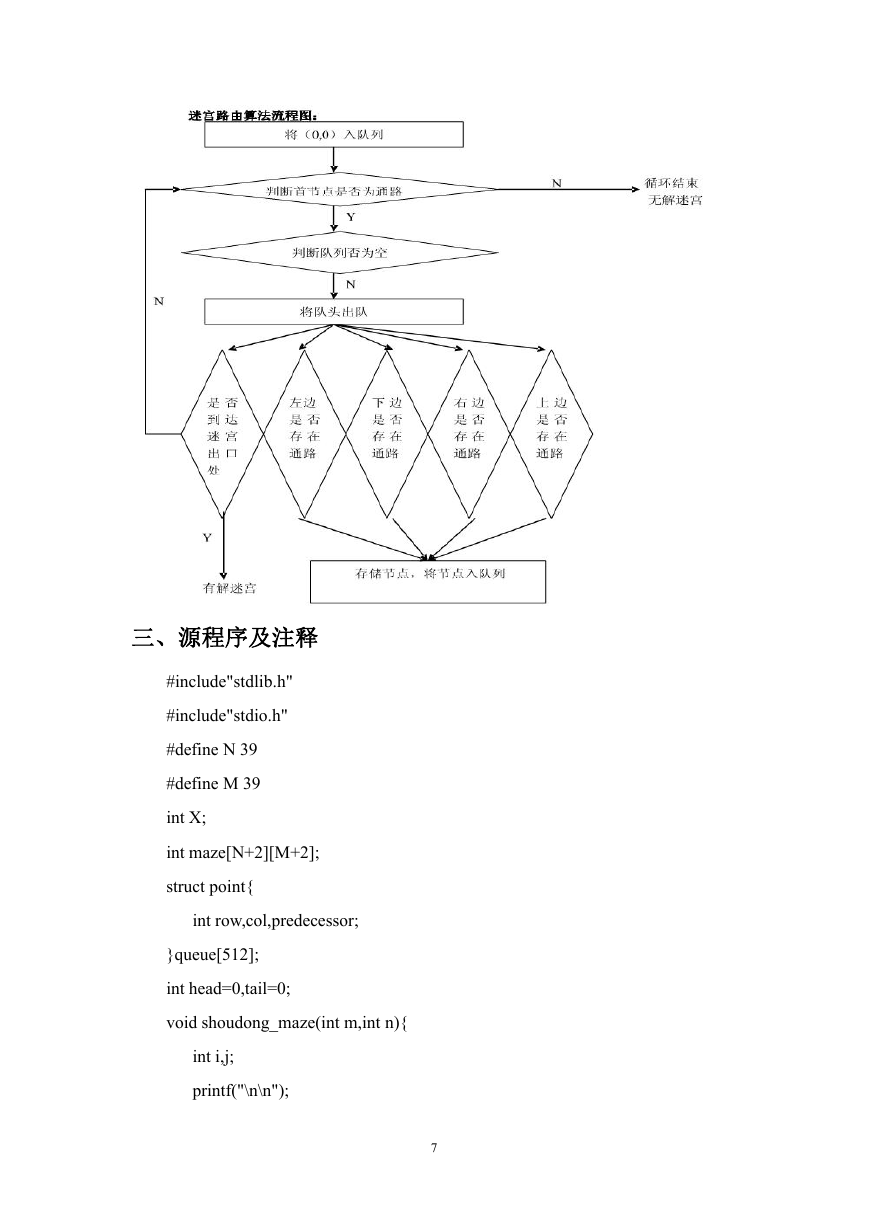
一、课程名称迷宫问题二、课题设计的基本思想，原理和算法描述由于计算机解迷宫时，通常用的是群举的方法，即从入口出发，顺某一方向搜索。若能走通，则继续往前走；否则沿原路退回，换一个方向再继续搜索，直至所有可能的通路都搜索完为止。为了保证在任何位置上都能沿原路返回，这就需要一个后进先出的结构来存储起位置，所以用到了栈的概念。在问题的求解过程中，用到了对栈的定义、栈的初始化、栈的空间的申情、栈的销毁等有关栈的知识。通过这次课程设计可让我们更深一步的了解栈的概念。在解决问题的过程中初步懂的如何去选择合适的方法去处理问题，提高解决问题的效率。 1.①构建一个二维数组 maze[M+2][N+2]用于存储迷宫矩阵 ②自动或手动生成迷宫，即为二维数组 maze[M+2][N+2]赋值 ③构建一个队列用于存储迷宫路径 ④建立迷宫节点 struct point,用于存储迷宫中每个节点的访问情况 ⑤实现搜索算法 ⑥屏幕上显示操作菜单 2.本程序包含 10 个函数： (1)主函数 main() (2)手动生成迷宫函数 shoudong_maze() (3)自动生成迷宫函数 zidong_maze() (4)将迷宫打印成图形 print_maze() (5)打印迷宫路径 (若存在路径) result_maze() (6)入队 enqueue() (7)出队 dequeue() (8)判断队列是否为空 is_empty() 2

(9)访问节点 visit() (10)搜索迷宫路径 mgpath() 3.3 详细设计实现概要设计中定义的所有数据类型及操作的伪代码算法 1. 节点类型和指针类型迷宫矩阵类型：int maze[M+2][N+2];为方便操作使其为全局变量迷宫中节点类型及队列类型：struct point{int row,col,predecessor} que[512] 2. 迷宫的操作 (1)手动生成迷宫 void shoudong_maze(int m,int n) {定义 i,j 为循环变量 for(i<=m) for(j<=n) 输入 maze[i][j]的值 } (2)自动生成迷宫 void zidong_maze(int m,int n) {定义 i,j 为循环变量 for(i<=m) for(j<=n) maze[i][j]=rand()%2 //由于 rand()产生的随机数是从 0 到 RAND_MAX,RAND_MAX 是定义在 stdlib.h 中的 , 其值至少为 32767),要产生从 X 到 Y 的数, 只需要这样写： k=rand()%(Y-X+1)+X; } (3)打印迷宫图形 3

void print_maze(int m,int n) {用 i,j 循环变量，将 maze[i][j]输出 □、■} (4)打印迷宫路径 void result_maze(int m,int n) {用 i,j 循环变量，将 maze[i][j]输出 □、■、☆} (5)搜索迷宫路径 ①迷宫中队列入队操作 void enqueue(struct point p) {将 p 放入队尾，tail++} ②迷宫中队列出队操作 struct point dequeue(struct point p) {head++,返回 que[head-1]} ③判断队列是否为空 int is_empty() {返回 head==tail 的值，当队列为空时，返回 0} ④访问迷宫矩阵中节点 void visit(int row,int col,int maze[41][41]) { 建立新的队列节点 visit_point, 将其值分别赋为 row,col,head-1,maze[row][col]=2,表示该节点以被访问过;调用 enqueue(visit_point),将该节点入队} ⑤路径求解 void mgpath(int maze[41][41],int m,int n) { 先定义入口节点为 struct point p={0,0,-1}, 从 maze[0][0]开始访问。如果入口处即为障碍，则此迷宫无解，返回 0 ，程序结束。否则访问入口节点，将入口节点标记为访问过 maze[p.row][p.col]=2, 调用函数 enqueue(p)将该节点入队。判断队列是否为空，当队列不为空时，则运行以下操作： { 调用 dequeue()函数，将队头元素返回给 p， 4

如果 p.row==m-1 且 p.col==n-1,即到达出口节点，即找到了路径，结束如果 p.col+10 且 maze[p.row][p.col-1]==0,说明未到迷宫左边界，且其左方有通路 , 则 visit(p.row,p.col-1,maze),将左方节点入队标记已访问如果 p.row-1>0 且 maze[p.row-1][p.col]==0,说明未到迷宫上边界，且其上方有通路 , 则 visit(p.row,p.col+1,maze),将上方节点入队标记已访问 } 访问到出口(找到路径)即 p.row==m-1 且 p.col==n-1,则逆序将路径标记为 3 即 maze[p.row][p.col]==3; while(p.predecessor!=-1) {p=queue[p.predecessor]; maze[p.row][p.col]==3;} 最后将路径图形打印出来。 3.菜单选择 while(cycle!=(-1)) ☆ 手动生成迷宫请按：1 ☆ 自动生成迷宫请按：2 5

☆ 退出请按：3 scanf("%d",&i); switch(i) { case 1：请输入行列数(如果超出预设范围则提示重新输入) shoudong_maze(m,n); print_maze(m,n); mgpath(maze,m,n); if(X!=0) result_maze(m,n); case 2 ：请输入行列数(如果超出预设范围则提示重新输入) zidong_maze(m,n); print_maze(m,n); mgpath(maze,m,n); if(X!=0) result_maze(m,n); case 3：cycle=(-1); break; } 4、函数关系调用图 6

三、源程序及注释 #include"stdlib.h" #include"stdio.h" #define N 39 #define M 39 int X; int maze[N+2][M+2]; struct point{ int row,col,predecessor; }queue[512]; int head=0,tail=0; void shoudong_maze(int m,int n){ int i,j; printf("\n\n"); 7

printf("请按行输入迷宫，0 表示通路，1 表示障碍:\n\n"); for(i=0;i

分享到：

赞收藏

资料库

数据结构课程设计报告迷宫游戏.doc

相关推荐

课程资源

热门标签

最新资料