Wallace 树乘法器专题研究 绪论：在乘法器的设计中采用树形乘法器，可以减少关键路径和所需的加法器单元数目， Wallace 树乘法器就是其中的一种。下面以一个 4*4 位乘法器为例介绍 Wallace 树乘法器及 其 Verilog HDL 实现。 原理：Wallace 树乘法器的运算原理如下： 从数据最密集的地方开始，不断的反复使用全加器、半加器来覆盖“树”。全加器是一个 3 输入 2 输出的器件，因此全加器又称作 3—2 压缩器。通过全加器将树的深度不断缩减，最 终缩减为一个深度为 2 的树。最后一级则采用简单的 2 输入加法器组成。 部分积 被乘数 乘数 X3 Y3 X3y0 (a[6]) X2y1 (a[7]) X1y2 (a[8]) X0y3 (a[9]) X3y2 (a[13]) X2y3 (a[14]) X3y3 (a[15]) X3y1 (a[10]) X2y2 (a[11]) X1y3 (a[12]) 第一级 6 X3y3 (a[15]) 5 X3y2 (a[13]) X2y3 (a[14]) 加法器结 果 4 X3y1 (a[10]) X2y2 (a[11]) X1y3 (a[12]) [1 : 0] b1 3 X3y0 (a[6]) X2y1 (a[7]) X1y2 (a[8]) X0y3 (a[9]) [1 : 0] b0 X0 Y0 X0y0 (a[0]) X1 Y1 X1y0 (a[1]) X0y1 (a[2]) 0 X0y0 (a[0]) 1 X1y0 (a[1]) X0y1 (a[2]) X2 Y2 X2y0 (a[3]) X1y1 (a[4]) X0y2 (a[5]) 2 X2y0 (a[3]) X1y1 (a[4]) X0y2 (a[5]) 注：对第一级的绿色部分，即 a[8]和 a[9]，以及 a[11]和 a[12]，使用半加器进行处理， 其 verilog HDL 代码体现如下： 

1. 2. hadd U1(.x(a[8]), .y(a[9]), .out(b0)); //2 输入半加器（第一级） hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级 输出分别为 b0 和 b1 。 第二级 6 X3y3 (a[15]) 5 X3y2 (a[13]) X2y3 (a[14]) b1[1] 4 X3y1 (a[10]) b1[0] b0[1] 3 X3y0 (a[6]) X2y1 (a[7]) b0[0] 加法器结 果 [1 : 0] C3 [1 : 0] C2 [1 : 0] C1 0 X0y0 (a[0]) 1 X1y0 (a[1]) X0y1 (a[2]) 2 X2y0 (a[3]) X1y1 (a[4]) X0y2 (a[5]) [1 : 0] C0 注：半加器仍然用绿色部分表示，全加器用橙色部分表示，第二级经过半加器以及全加器的 处理后，到达第三级。 其 verilog HDL 代码体现如下： 1. 2. 3. 4. 第三级 6 X3y3 (a[15]) C3[1] hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级 fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3 输入全加器（第二级） fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2)); fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3)); 5 C3[0] C2[1] 4 C2[0] C1[1] 3 C1[0] C0[1] 2 X2y0 (a[3]) C0[0] 0 X0y0 (a[0]) 1 X1y0 (a[1]) X0y1 (a[2]) 注：第三级树的深度减少到 2，采用简单的 2 输入加法器即可得到最后的结果。 其在 verilog HDL 代码中的体现如下： 1. 2. 3. 4. assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器（第三极） assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]}; assign add_out = add_a + add_b; assign out = {add_out,a[0]}; 

parameter size = 4; //定义参数，乘法器的位数 input [size - 1 : 0] x,y; //输入 y 是乘数，x 是被乘数 output [2*size - 1 : 0] out; wire [size*size - 1 : 0] a; //a 为部分积 wire [1 : 0] b0, b1; //第一级的输出，包含进位 wire [1 : 0] c0, c1, c2, c3; //第二级的输出，包含进位 wire [5 : 0] add_a, add_b; //第三极的输入 wire [6 : 0] add_out; //第三极的输出 wire [2*size - 1 : 0] out; //乘法器的输出（组合逻辑） assign a = {x[3],x[2],x[3],x[1],x[2],x[3],x[0],x[1], x[2],x[3],x[0],x[1],x[2],x[0],x[1],x[0]} &{y[3],y[3],y[2],y[3],y[2],y[1],y[3],y[2] ,y[1],y[0],y[2],y[1],y[0],y[1],y[0],y[0]}; //部分积 hadd U1(.x(a[8]), .y(a[9]), .out(b0)); //2 输入半加器（第一级） hadd U2(.x(a[11]), .y(a[12]), .out(b1));//第一级 hadd U3(.x(a[4]), .y(a[5]), .out(c0)); //第二级 fadd U4(.x(a[6]), .y(a[7]), .z(b0[0]), .out(c1)); //3 输入全加器（第二级） fadd U5(.x(b1[0]), .y(a[10]), .z(b0[1]), .out(c2)); fadd U6(.x(a[13]), .y(a[14]), .z(b1[1]), .out(c3)); assign add_a = {c3[1],c2[1],c1[1],c0[1],c0[0],a[2]}; //加法器（第三极） assign add_b = {a[15],c3[0],c2[0],c1[0],a[3],a[1]}; assign add_out = add_a + add_b; assign out = {add_out,a[0]}; Verilog HDL 描述： 整个电路的 verilog HDL 设计代码如下： module wallace(x,y,out); 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. endmodule 32. 33. //全加器模块 34. module fadd(x, y, z, out); 35. 36. 37. 38. endmodule 39. 40. //半加器模块 41. module hadd(x, y, out); input x, y, z; output [1 : 0] out; assign out = x + y + z; 

input x, y; output [1 : 0] out; assign out = x + y; 42. 43. 44. 45. endmodule Testbench（测试） 文件代码如下： //测试文件 `timescale 1ns/1ps module wallace_tb; reg [3 : 0] x, y; wire [7 : 0] out; wallace U1(.x(x), .y(y), .out(out)); //模块实例 initial begin 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. endmodule end x = 3; y = 4; # 20 x = 2; y = 3; # 20 x = 6; y = 8; 用 Modelsim 仿真软件仿真图波形图如下： （此图可放大观看） 测试发现，结果符合预期结果。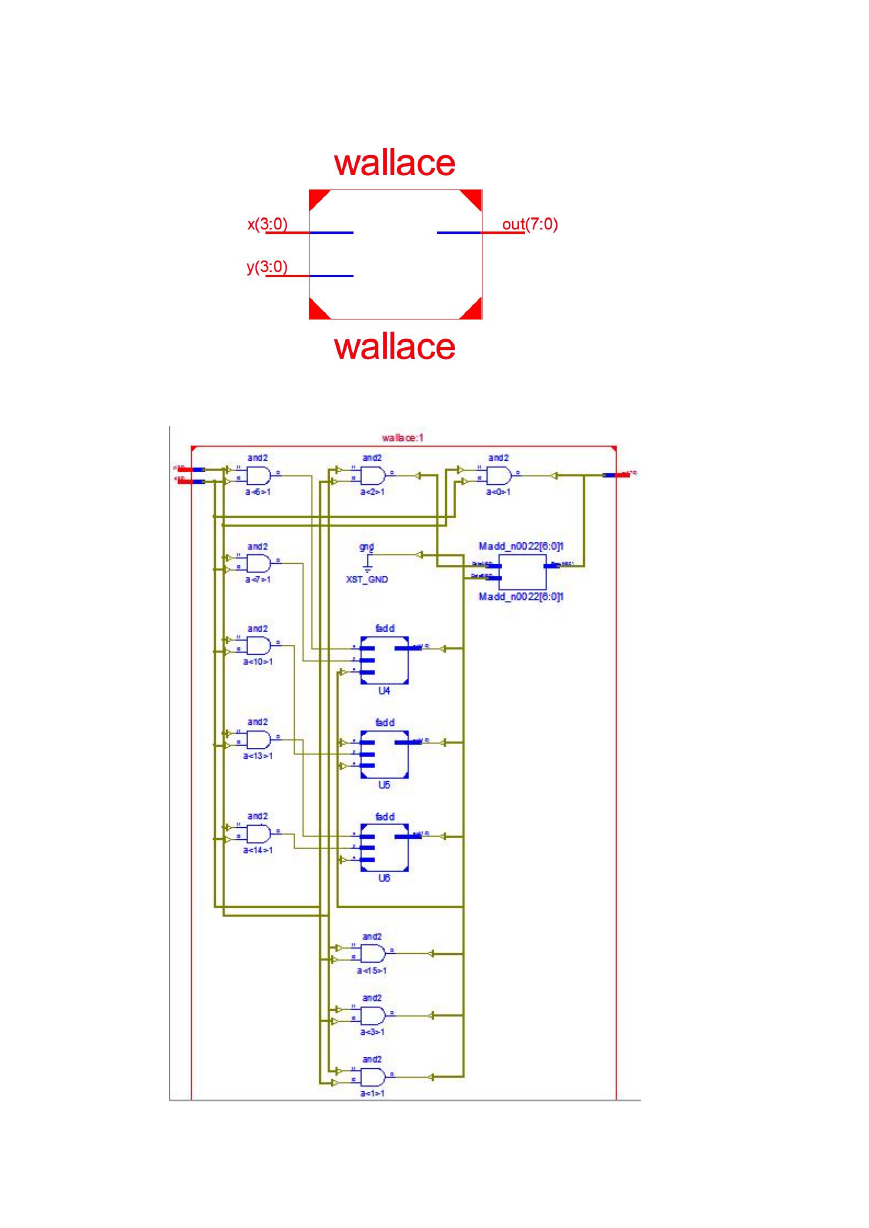 在 ISE 软件中仿真，其 RTL Schematic 如下：