logo资料库

三角形问题白盒测试技术实验报告.docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.13M 资料格式：docx 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    1.代码走读
    从代码来看，main()存在多个Scanner语句，会导致程序的多入口，但代码中存在多个System
    从程序结构来看，整个程序有两个判定结构，且两个判定结构为结构化设计，便于测试，每个判定结点出的判定表
    2.静态结构分析（函数控制流图法）
    如图：
    从该图可以看出，该函数的结构设计特点：多出口，有两个函数出口；环复杂度高，判定节点一次为P1到P5,
    3. 对判定的测试
    （1）函数流程图
    （2）语句覆盖？判定翻盖？条件覆盖？条件组合覆盖？判定/条件覆盖？修正的判定/条件覆盖（选1-2种覆
    选择判定覆盖语句 ;
    选择理由:基于判定覆盖指标的测试因需覆盖到每一条执行边，生成的测试用例数量相对语句覆盖有所增加，且测
    （3）测试用例设计
    4.对路径的测试
    （1）程序图
    1代表代码1到8行；2代表代码9到14行；3代表15行；4代表16行；5代表17行；6代表35到37
    （2）环复杂度
    由图可知判定结点数为5。
    则V(G)=区域数=判定节点数+1=5+1=6
    （3）独立路径的抽取
    路径1：1,2,3,4,5,6,9,10,12
    路径2：1,2,3,4,5,6,9,11,12
    路径3：1,2,3,4,5,6,8,12
    路径4：1,2,3,4,5,7,12
    路径5：1,2,3,4,7,12
    路径6：1,2,3,7,12
    （4）不可行路径的处理
    通过查看代码无不可行路径。
    （5）测试用例设计
    5.对变量的测试
    （1）寻找所有变量的定义节点和使用节点
    （2）确定各变量的定义/使用节点对，并考查每条路径
    对变量pd分析：定义使用节点队为（7,7）是定义清除路径
    对变量a分析：定义使用节点队为（2,3）,（2,6），（2,9）是定义清除路径
    对变量b分析：定义使用节点队为（2,4），（2,6），（2,9）是定义清除路径
    对变量c分析：定义使用节点队为（2,5），（2,6），（2,9）是定义清除路径
    6.对循环的测试（选做，分配到的代码中有循环要做对循环的测试，没有循环就不做）
    无循环
    白盒测试技术实验报告 一、实验内容 1、系统地学习和理解白盒测试的基本概念、原理，掌握白盒测试的基本技 术和方法； 2、举例进行白盒测试，使用语句覆盖、判定覆盖、条件覆盖、判定/条件覆 盖、组合覆盖、路径覆盖进行测试。 3、通过试验和应用，要逐步提高和运用白盒测试技术解决实际测试问题的 能力； 4、完成实验并认真填写实验报告 二、问题描述 输入三个整数 a、b、c，分别作为三角形的三条边，通过程序判断这三条边 是否能构成三角形？如果能构成三角形，则判断三角形的类型（等边三角形、等 腰三角形、一般三角形）。要求输入三个整数 a、b、c，必须满足以下条件：1≤a≤200； 1≤b≤200；1≤c≤200。请采用静态白盒测试方法和动态白盒测试方法设计测试用 例。 三、代码说明（复制测试的主要代码并在每行程序代码前面标上行号） 1 package rjcs; 2 import java.util.Scanner; 3 public class Rjcs { 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public static void main(String[] args) { // TODO 自动生成的方法存根 @SuppressWarnings("resource") Scanner sc = new Scanner(System.in); //接受键盘输入a,b,c System.out.println("请键盘输入a的值"); int a = sc.nextInt(); System.out.println("请键盘输入b的值"); int b = sc.nextInt(); System.out.println("请键盘输入c的值"); int c = sc.nextInt(); if(a>=1&&a<=200) { if(b>=1&&b<=200) { if(c>=1&&c<=200) { test(a,b,c);
    19 20 21 22 23 24 25 26 27 28 29 30 31 } else { System.out.println("请输入能构成三角形的整数！"); } } else { System.out.println("请输入能构成三角形的整数！"); } } else { System.out.println("请输入能构成三角形的整数！"); } } public static void test(int a,int b,int c){ boolean pd=false; if((a==b)&&(b==c)){ System.out.println("三边构成等边三角形"); } else if((a==b)||(b==c)||(a==c)){ System.out.println("三边构成等腰三角形"); System.out.println("三边构成一般三角形"); } else System.out.println("请输入能构成三角形的整数！") 32//判断三角形类型 33 34 35 36 37 38 39 40 41 42 43 44 45 46} } } else{ 四、白盒测试分析 1.代码走读
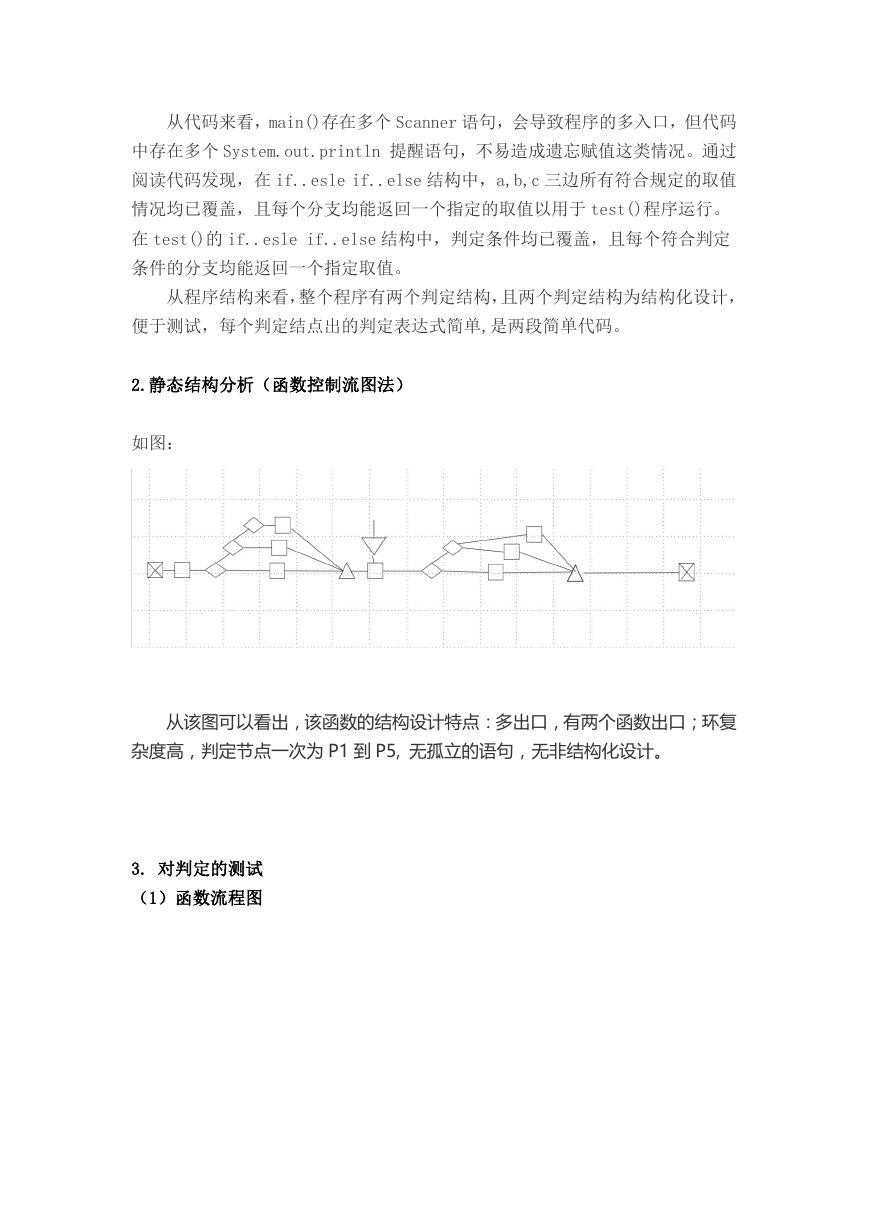
    从代码来看，main()存在多个 Scanner 语句，会导致程序的多入口，但代码 中存在多个 System.out.println 提醒语句，不易造成遗忘赋值这类情况。通过 阅读代码发现，在 if..esle if..else 结构中，a,b,c 三边所有符合规定的取值 情况均已覆盖，且每个分支均能返回一个指定的取值以用于 test()程序运行。 在 test()的 if..esle if..else 结构中，判定条件均已覆盖，且每个符合判定 条件的分支均能返回一个指定取值。 从程序结构来看，整个程序有两个判定结构，且两个判定结构为结构化设计， 便于测试，每个判定结点出的判定表达式简单,是两段简单代码。 2.静态结构分析（函数控制流图法） 如图： 从该图可以看出，该函数的结构设计特点：多出口，有两个函数出口；环复 杂度高，判定节点一次为 P1 到 P5, 无孤立的语句，无非结构化设计。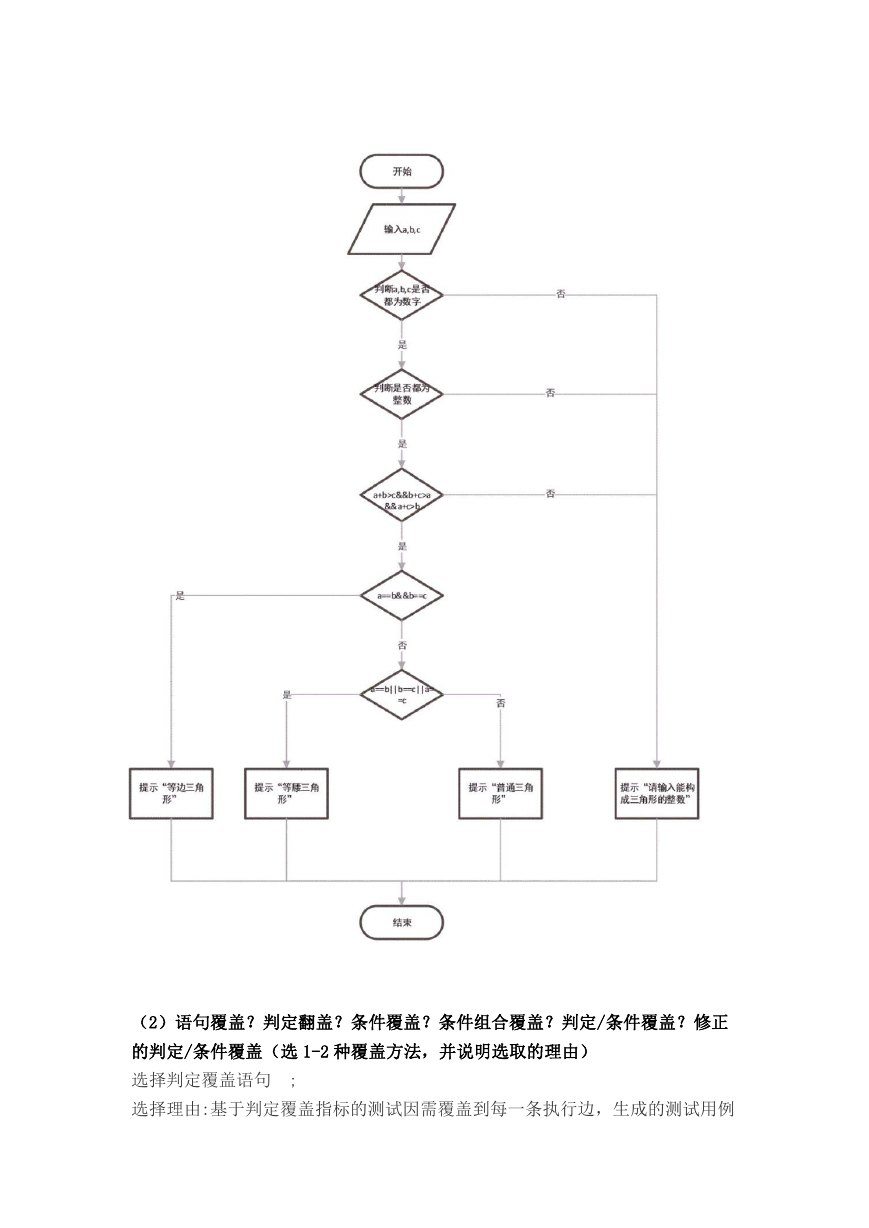 3. 对判定的测试 （1）函数流程图
    （2）语句覆盖？判定翻盖？条件覆盖？条件组合覆盖？判定/条件覆盖？修正 的判定/条件覆盖（选 1-2 种覆盖方法，并说明选取的理由） 选择判定覆盖语句 ; 选择理由:基于判定覆盖指标的测试因需覆盖到每一条执行边，生成的测试用例
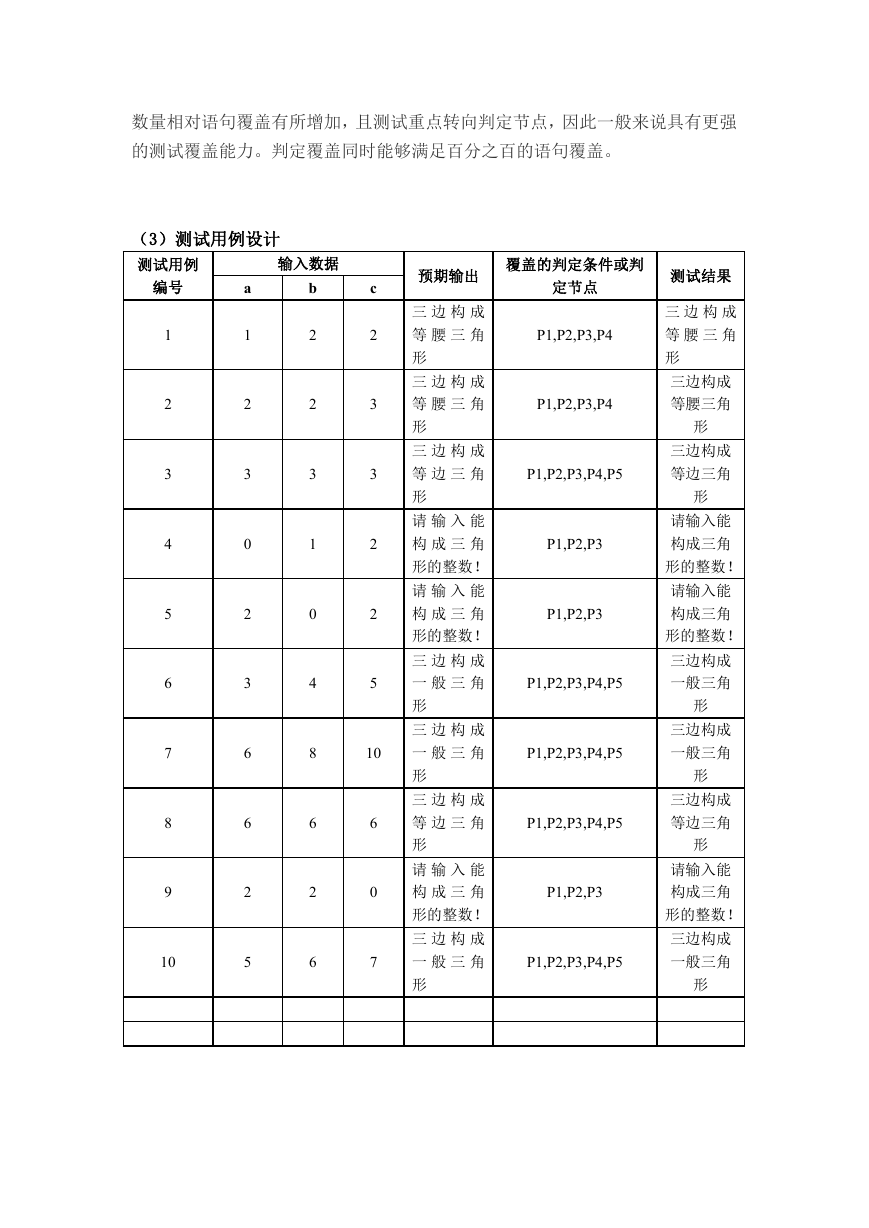
    数量相对语句覆盖有所增加，且测试重点转向判定节点，因此一般来说具有更强 的测试覆盖能力。判定覆盖同时能够满足百分之百的语句覆盖。 （3）测试用例设计 测试用例 编号 1 2 3 4 5 6 7 8 9 10 a 1 2 3 0 2 3 6 6 2 5 输入数据 b 2 2 3 1 0 4 8 6 2 6 c 2 3 3 2 2 5 10 6 0 7 预期输出 三 边 构 成 等 腰 三 角 形 三 边 构 成 等 腰 三 角 形 三 边 构 成 等 边 三 角 形 请 输 入 能 构 成 三 角 形的整数！ 请 输 入 能 构 成 三 角 形的整数！ 三 边 构 成 一 般 三 角 形 三 边 构 成 一 般 三 角 形 三 边 构 成 等 边 三 角 形 请 输 入 能 构 成 三 角 形的整数！ 三 边 构 成 一 般 三 角 形 覆盖的判定条件或判 定节点 P1,P2,P3,P4 P1,P2,P3,P4 P1,P2,P3,P4,P5 P1,P2,P3 P1,P2,P3 P1,P2,P3,P4,P5 P1,P2,P3,P4,P5 P1,P2,P3,P4,P5 P1,P2,P3 P1,P2,P3,P4,P5 测试结果 三 边 构 成 等 腰 三 角 形 三边构成 等腰三角 形 三边构成 等边三角 形 请输入能 构成三角 形的整数！ 请输入能 构成三角 形的整数！ 三边构成 一般三角 形 三边构成 一般三角 形 三边构成 等边三角 形 请输入能 构成三角 形的整数！ 三边构成 一般三角 形
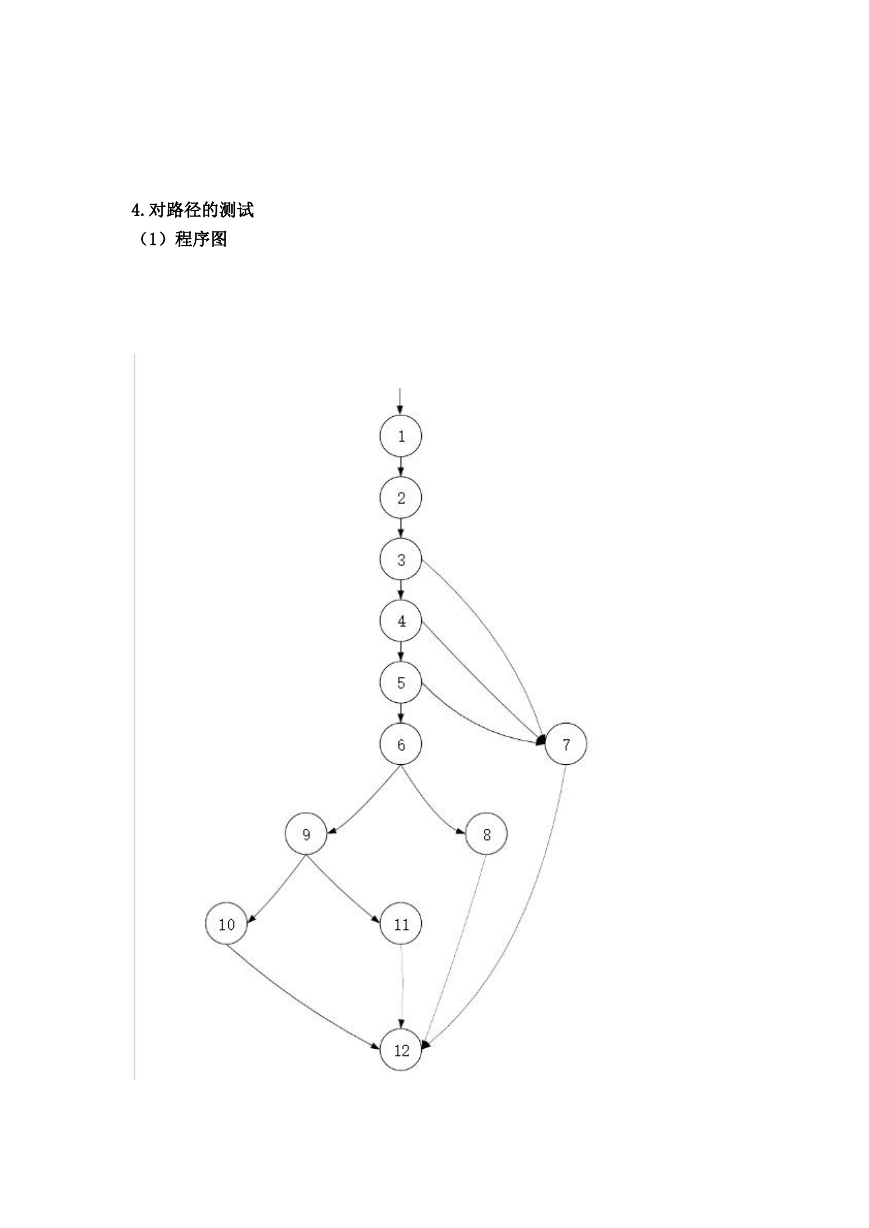
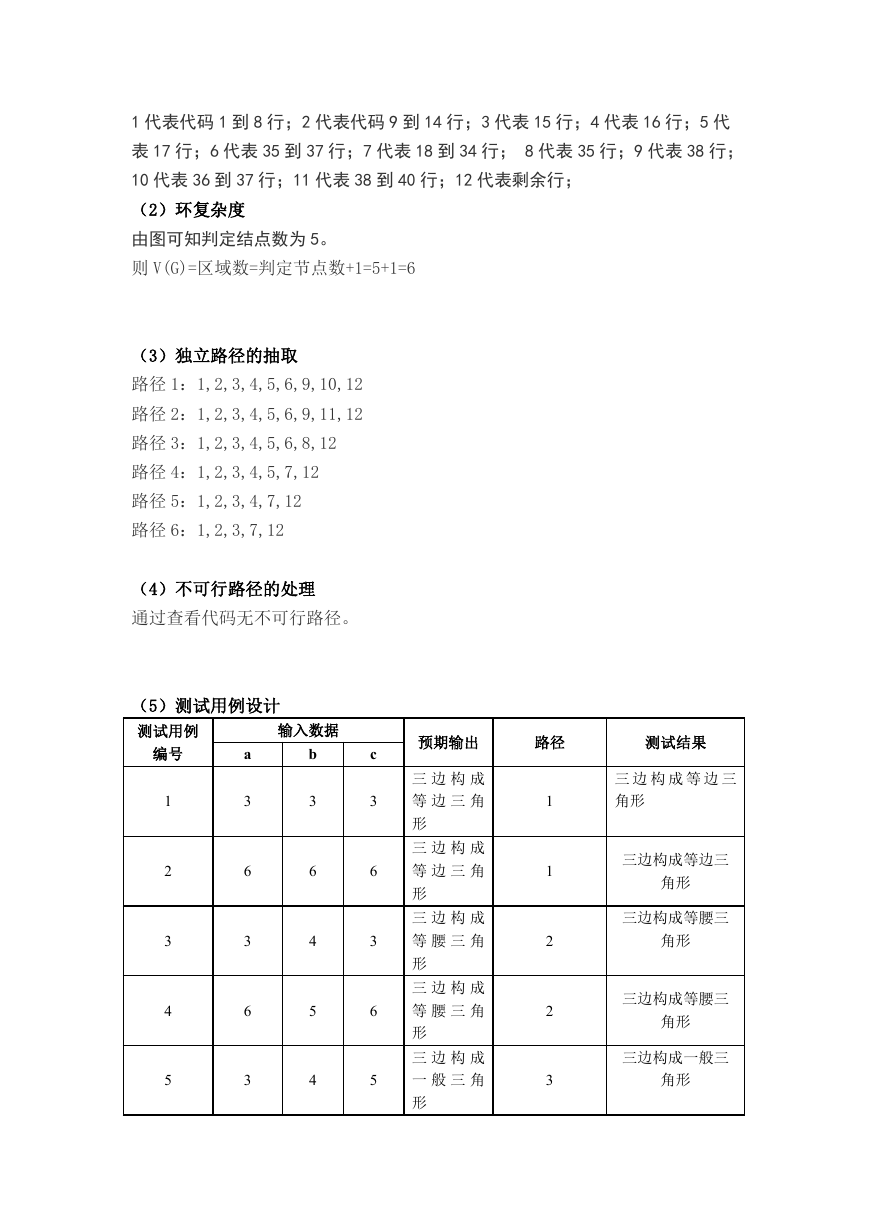
    4.对路径的测试 （1）程序图
    1 代表代码 1 到 8 行；2 代表代码 9 到 14 行；3 代表 15 行；4 代表 16 行；5 代 表 17 行；6 代表 35 到 37 行；7 代表 18 到 34 行； 8 代表 35 行；9 代表 38 行； 10 代表 36 到 37 行；11 代表 38 到 40 行；12 代表剩余行； （2）环复杂度 由图可知判定结点数为 5。 则 V(G)=区域数=判定节点数+1=5+1=6 （3）独立路径的抽取 路径 1：1,2,3,4,5,6,9,10,12 路径 2：1,2,3,4,5,6,9,11,12 路径 3：1,2,3,4,5,6,8,12 路径 4：1,2,3,4,5,7,12 路径 5：1,2,3,4,7,12 路径 6：1,2,3,7,12 （4）不可行路径的处理 通过查看代码无不可行路径。 （5）测试用例设计 测试用例 编号 1 2 3 4 5 a 3 6 3 6 3 输入数据 b 3 6 4 5 4 c 3 6 3 6 5 预期输出 路径 测试结果 三 边 构 成 等 边 三 角 形 三 边 构 成 等 边 三 角 形 三 边 构 成 等 腰 三 角 形 三 边 构 成 等 腰 三 角 形 三 边 构 成 一 般 三 角 形 1 1 2 2 3 三 边 构 成 等 边 三 角形 三边构成等边三 角形 三边构成等腰三 角形 三边构成等腰三 角形 三边构成一般三 角形
    6 7 8 5 5 0 6 0 5 5.对变量的测试 0 6 6 请 输 入 能 构 成 三 角 形的整数！ 请 输 入 能 构 成 三 角 形的整数！ 请 输 入 能 构 成 三 角 形的整数！ 4 5 6 请输入能构成三 角形的整数！ 请输入能构成三 角形的整数！ 请输入能构成三 角形的整数！ （1）寻找所有变量的定义节点和使用节点 变量 定义节点 使用节点 a b c pd 2 2 2 7 3,6,9 4,6,9 5,6,9 7 定义/使用节点 2 2 2 7 （2）确定各变量的定义/使用节点对，并考查每条路径 对变量 pd 分析：定义使用节点队为（7,7）是定义清除路径 对变量 a 分析：定义使用节点队为（2,3）,（2,6），（2,9）是定义清除路径 对变量 b 分析：定义使用节点队为（2,4），（2,6），（2,9）是定义清除路径 对变量 c 分析：定义使用节点队为（2,5），（2,6），（2,9）是定义清除路径 6.对循环的测试（选做，分配到的代码中有循环要做对循环的测试，没有循环 就不做） 无循环
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料