使用AnyLogic
多方法仿真建模
此文档是AnyLogic
标准培训计划
© The AnyLogic Company | www.anylogic.com
�
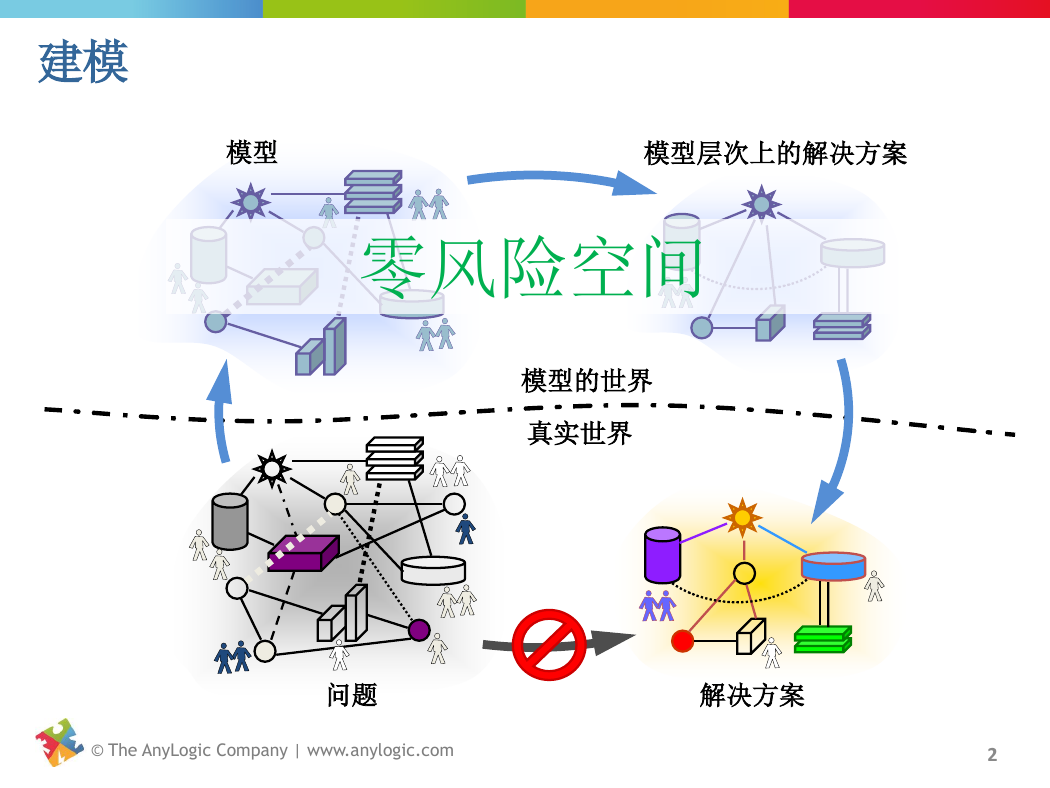
建模
模型
模型层次上的解决方案
零风险空间
模型的世界
真实世界
问题
?
解决方案
© The AnyLogic Company | www.anylogic.com
2
�
模型的种类
心智模型
用线连接的方框
物质模型
一张纸的公式
Excel电子表格
仿真模型
© The AnyLogic Company | www.anylogic.com
3
�
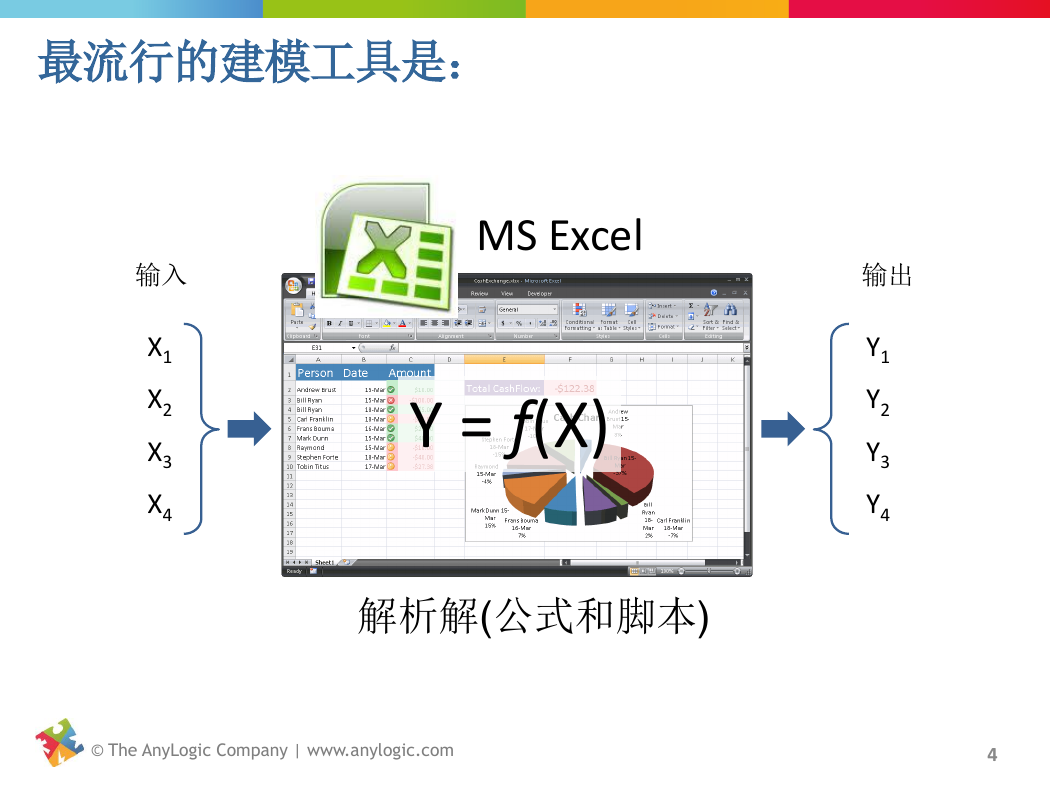
最流行的建模工具是:
输入
X1
X2
X3
X4
MS Excel
Y = f(X)
解析解(公式和脚本)
输出
Y1
Y2
Y3
Y4
© The AnyLogic Company | www.anylogic.com
4
�
但是…
• 你能够找到解析解,如果:
•参数数量可控
•行为是线性的
•有明确的依赖性,容易建立心智模型
• 但是如果:
•参数过多
•非线性,非明显影响
•时间和因果依赖
•反常的行为
•不确定性 (随机系统)
?
© The AnyLogic Company | www.anylogic.com
5
�
示例: 银行
• 一个简单的案例:
•平均每小时10位客户
•柜台只有一名柜员
•平均服务时间为5分钟
• 我们想找出:
•排队平均等待时间
•[可以从此推导出的其他指标]
• 你将花费几秒钟找到解析解:
平均等待时间*
, 其中
- 到达率
- 平均服务时间
* 这只适用于泊松流客户(以恒定速率独立到达)和指数分布的服务时间。
© The AnyLogic Company | www.anylogic.com
6
bbw12b�
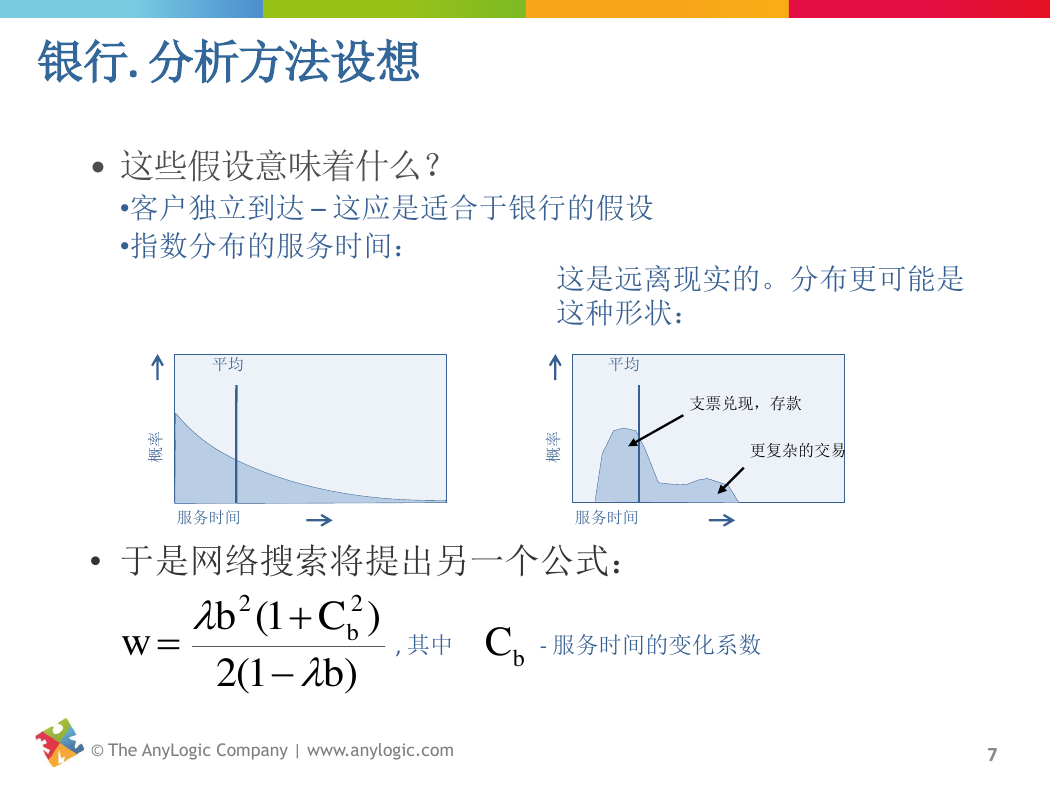
银行. 分析方法设想
• 这些假设意味着什么?
•客户独立到达 – 这应是适合于银行的假设
•指数分布的服务时间:
这是远离现实的。分布更可能是
这种形状:
平均
平均
率
概
率
概
支票兑现,存款
更复杂的交易
服务时间
服务时间
• 于是网络搜索将提出另一个公式:
, 其中
- 服务时间的变化系数
© The AnyLogic Company | www.anylogic.com
7
)1(2)1(22bCbwbbC�
银行. 如果不是简单的案例?
• 有几个(K) 出纳员
•这就是所谓的“多服务排队模型”。解析解*: vvfgx
, 其中
- 系统利用率,
, 其中
- 所有出纳员都忙碌的概率
- “银行里没有客户”的概率
* 但是,这只适用于泊松流客户和指数分布的服务时间。
• 如果服务时间有不同的分布?
̶ 即使对于这样一个简单系统,也没有解析解。
© The AnyLogic Company | www.anylogic.com
8
1KPbwKb0)1(!PKKPK1100!)1(!KiiKiKKKP�













 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc