第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
三角形单元到四边形单元的自动转化.pdf
Automatic Conversion of Triangular Meshes Into Quadrilateral Meshes with Directionality
Takayuki Itoh1* and Kenji Shimada2
1IBM Research, Tokyo Research Laboratory 2Mechanical Engineering, Carnegie Mellon University
Abstract - This paper presents a triangular-to-quadrilateral mesh conversion method that can cont...
Keywords:quadrilateral mesh, triangular mesh, conversion, directionality.
1.Introduction
2.Previous Work
3.Preliminaries
4.Mesh Conversion with Directionality
5.Results
6.Conclusion
References
International Journal of CAD/CAM Vol. 1, No. 1, pp. 11~21 (2002)
Automatic Conversion of Triangular Meshes Into Quadrilateral Meshes with
Directionality
Takayuki Itoh1* and Kenji Shimada2
1IBM Research, Tokyo Research Laboratory
2Mechanical Engineering, Carnegie Mellon University
Abstract - - - - This paper presents a triangular-to-quadrilateral mesh conversion method that can control the directionality of the
output quadrilateral mesh according to a user-specified vector field. Given a triangular mesh and a vector field, the method
first scores all possible quadrilaterals that can be formed by pairs of adjacent triangles, according to their shape and
directionality. It then converts the pairs into quadrilateral elements in order of the scores to form a quadrilateral mesh.
Engineering analyses with finite element methods occasionally require a quadrilateral mesh well aligned along the boundary
geometry or the directionality of some physical phenomena, such as in the directions of a streamline, shock boundary, or force
propagation vectors. The mesh conversion method can control the mesh directionality according to any desired vector fields,
and the method can be used with any existing triangular mesh generators.
Keywords: quadrilateral mesh, triangular mesh, conversion, directionality.
1. Introduction
In some types of finite element method (FEM)
analyses, such as sheet-metal forming simulations and
automobile crash simulations, quadrilateral meshes are
preferable to triangular meshes because they produce
more accurate results more efficiently. Such engineering
analyses occasionally require a quadrilateral mesh well
aligned along the boundary geometry or the directionality
of some physical phenomena, such as along the directions
of a streamline, shock boundary, or force propagation
vectors.
Although there are many approaches to generating
quadrilateral meshes, their capabilities of controlling
the mesh directionality are quite limited. The existing
quadrilateral meshing approaches include: template
matching [1], medial-axis-based decomposition [2], quad-
tree decomposition [3-5], advancing front [6-10], and
triangular-to-quadrilateral mesh conversion [11-21]. In
this paper we focus on the triangle-to-quadrilateral mesh
conversion methods, which take advantage of the benefits
of triangular mesh generation: (1) a fully-automated
meshing process, (2) flexible control of element sizes,
and (3) less computation time than the advancing front
method. The advancing front methods [6-10] and the
triangular-to-quadrilateral mesh conversion methods [18-
20] control mesh directionality, but based only on the
domain boundary; they cannot create a quadrilateral
mesh that aligns well with an arbitrary vector field
*Corresponding author:
E-mail : itot@trl.ibm.com
given by the user.
In this paper we propose a triangular-to-quadrilateral
mesh conversion scheme that can control the mesh
directionality of an output quadrilateral mesh accurately
based on a user-specified vector field. Given a triangular
mesh and a vector field, the method generates a
quadrilateral mesh. It first scores the geometric irregularity
and the directionality error of the quadrilaterals formed
by all possible pairs of adjacent triangular elements in
the input mesh. It then converts pairs of adjacent
triangular elements into quadrilateral elements according
to the weighted sum of the shape irregularity and the
directionality error. The proposed conversion method
can be used with any existing triangular mesh generators.
The remainder of the paper is organized as follows.
After reviewing previous mesh conversion methods in
Section 2, we describe data structures for triangular
meshes and vector fields in Section 3. We then describe
the algorithm of our mesh conversion method in Section
4. After discussing our results in Section 5, we offer
some conclusions in Section 6.
2. Previous Work
Given a triangular mesh, existing triangular-to-
quadrilateral mesh conversion methods [11-21] join
pairs of adjacent triangular elements selectively and then
convert the pairs into quadrilateral elements. The quality
of the output quadrilateral mesh strongly depends on
which pairs of triangular elements are joined. The
shapes of the quadrilateral elements and the number of
triangular elements left in quad-dominant meshes strongly
International Journal of CAD/CAM Vol. 1, No. 1, pp. 11~21
depend on this selection of triangular pairs.
One of the goals of triangular-to-quadrilateral mesh
conversion is to maximize the number of triangular
pairs. This problem is called maximum matching in graph
theory, and there are algorithms available for solving
this problem. Suppose the connectivity of input triangular
elements is interpreted as an undirected weighted graph,
the graph nodes represent triangular mesh elements,
and graph edges represent connectivity between mesh
elements. Preferable quadrilateral meshes can be obtained
by applying a maximum matching algorithm to non-
bipartite graphs. This process, however, is computationally
expensive, and it does not necessarily create a quad-
dominant mesh suitable for engineering analysis. Another
approach to solving the mesh conversion problem is to
apply integer programming [21], which is also com-
putationally expensive. In most cases a quadrilateral
mesh of sufficient quality for engineering analysis can
be generated without performing maximum matching
or integer programming, as can be seen in many
previously proposed mesh conversion methods.
In the rest of this section we survey and categorize
previous mesh conversion methods. Note that the
common shortfall of these methods is limited control
over mesh directionality. Some of the methods can
align an output mesh along the domain boundaries, but
none can realize a user-defined arbitrary directionality.
2.1. Conversion methods
that minimize
the
number of triangular elements
The methods in this category [11-12] count the
number of unprocessed adjacent triangles for each
triangle and mark those that have only one unprocessed
adjacent triangle as high-priority triangles. These triangles
are then extracted and converted into quadrilateral
elements with their adjacent triangles. The adjacency of
triangles is dynamically updated during the conversion
process, and many triangles are therefore marked as
high-priority triangles during the process. Finally, many
of the marked triangles are converted into quadrilateral
elements yielding a quad-dominant mesh.
Since the goal of these methods is to generate all-
quadrilateral meshes, they also include post-processing
for converting isolated triangles. Heighway [11] proposes
a method that swaps the edges of quadrilaterals lying
between two isolated triangles until the two triangles
become adjacent, as if the two triangles ‘walk’ toward
each other. Johnston et al. [12] describe a method that
subdivides or swaps edges of isolated triangles until they
are locally converted into all-quadrilateral elements.
2.2. Conversion methods that minimize geometric
irregularities
The methods in this category [13-17] first calculate
the values of a scalar function representing the shapes
of the quadrilaterals generated by all possible pairs of
adjacent triangular elements. They then convert the
triangle pairs into quadrilateral elements in order of the
values of this function.
Various functions can be used to evaluate quadrilateral
shapes. Lo et al. [13] propose an evaluation function
defined by the ratio between the shape evaluation
values of the four possible triangles generated by dividing
the quadrilateral by its two diagonals. Borouchaki et al.
[17] propose an evaluation function based on the angles
of the four vertices of each quadrilateral.
2.3. Advancing front-like conversion methods
In many cases, elements along the domain boundary
are the most critical in engineering analysis. Therefore,
it is often desirable that elements are well aligned along
the domain boundary. Quadrilateral meshes with such
well-aligned boundary elements can be generated via
triangular-to-quadrilateral mesh conversion by coupling
triangles of the input mesh along the domain boundary
first.
Shimada et al. [20] devised a method that first clusters
the input triangular mesh into layered sub-domains along
the domain boundary, and then couples the triangles in
each cluster. The method generates a topologically regular
mesh, and the mesh elements’ shapes can be improved
by a smoothing process.
Owen et al. [18-19] propose the ‘Q-Morph’ method,
which visits front of an input triangular mesh in order
and forms quadrilaterals along the visited front edges
by re-connecting some edges around the visited front
edges. This method generates a high quality quadrilateral
mesh well aligned along the domain boundary, similar
to a mesh generated by the advancing front method.
3. Preliminaries
In this section we define the data structures for the
inputs of the proposed mesh conversion method: a
triangular mesh and a desired mesh directionality.
3.1. Data structure of a triangular mesh
We represent a triangular mesh, Mt, as a planar graph,
Mt = (V, T, T, D T),
(1)
¶
consisting of four ordered lists of:
(1) nodes, V=(v1,..., vl),
(2) triangular elements, T=(t1,..., tn),
¶
(3) element boundaries, T=(
tn), which
defines the three surrounding nodes of each
triangle, and
(4) adjacent elements, D T=(D t1, ..., D tn), which gives
at most three adjacent triangles for each triangle.
¶
t1, ...,
¶
¶
V and T are topological entities in a triangular mesh,
and T and D T give topological connections between
topological entities. The i th element of T, denoted as
¶
ti, represents the counter-clockwise ordered list of the
nodes surrounding the i th triangle ti. Similarly, the i th
¶
Takayuki Itoh and Kenji Shimada
Automatic Conversion of Triangular Meshes Into Quadrilateral Meshes with Directionality
Fig. 1. Triangular mesh representation.
element of the list D T, denoted as D ti, represents the
counter-clockwise ordered list of the triangles adjacent
to the i th triangle ti. The notation D tij represents the j th
adjacent triangle of D ti. The number of adjacent triangles
of ti is denoted by |D ti|.
For example, the representation of the triangular mesh
shown in Fig. 1(a) is:
(2)
Mt=((v1, v2, v3, v4, v5), (t1, t2, t3),
((v1, v2, v3),)(v2, v4, v3), (v2, v5, v4)),
((f , t2, f ), (t3, f , t1), (f , f , t2))),
where f in D T means that there is no triangle adjacent
to a given side. In this example, as implied by the
expression D t1=(f , t2, f ), the triangle t1 has only one
adjacent triangle t2, so the number of adjacent triangles
is one, or |D t1|=1.
In the mesh conversion algorithms given in this paper,
adjacencies between triangles are selectively deleted in
order to make pairs of triangles. Fig. 1(a) shows an
example of nodes and triangles in a mesh, and Fig. 1(b)
shows its adjacencies. To delete the adjacency between
t2 and t3 in Fig. 1(b), D t21 and D t33 are set to f , yielding
a new element adjacency,
D T=((f , t2, f ), (f , f , t1), (f , f , f ))
as shown in Fig. 1(c).
(3)
Our mesh conversion method couples adjacent
triangles, ti and tj, while deleting the adjacency between
ti (or tj) and its other adjacent triangular elements. The
coupling process is repeated until no triangle has an
adjacency with more than one other triangular element.
Edges shared by each pair of triangles are then deleted,
and finally a quad-dominant mesh is generated.
Fig. 2. Quad-dominant to all-quad mesh conversion.
Although the quad-dominant mesh generated by this
mesh conversion method contains a small number of
triangular elements, it can be converted into an all-
quadrilateral mesh by dividing each remaining triangle
into three quadrilaterals and dividing each quadrilateral
into four quadrilaterals, by adding an inside node for
each triangle and by dividing all the edges in two for
both triangles and quadrilaterals, as shown in Fig. 2.
3.2. Data structure for desired mesh directionality
One of the inputs of our method is a vector field that
represents the user’s preferences for mesh directionality.
A simple way to represent a vector field is to use a grid
so that at each grid-point a vector value is defined. In
this paper we assume that the vector field is given as a
two-dimensional grid, G, represented as:
G=(PG, DG)
consisting of two ordered lists of:
(4)
(1) grid-points, PG=((p1,1,...,p1,n),.....,(pm,1,...,pm,n)), and
(2) vector values, DG=((d1,1,...,d1,n),....,(dm,1,...,dm,n)).
As shown in Fig. 3, the grid G has (m-1) (n-1) cells
and m n grid-points. The vector value, d, at an
arbitrary point, p, can be calculated by the following
Fig. 3. A 2D grid representing a vector field, and the calculation of a vector value at an arbitrary point.
International Journal of CAD/CAM Vol. 1, No. 1, pp. 11~21
bi-linear interpolation of vector values assigned to the
grid-points:
d(s,t)=(1-s)((1-t)di,j+tdi,(j+1))+s((1-t)d(i+1), j+td(i+1),(j+1))
(5)
where (s,t) is the parametric coordinate of point p
calculated by projecting a cell that contains point p.
4. Mesh Conversion with Directionality
This section describes the algorithm of our mesh
conversion method. Given a triangular mesh, Mt, and
desired mesh directionality, G, the method first scores
the shapes and directionality of all the possible
quadrilaterals that can be generated by combining pairs
of adjacent triangles. The method then converts the
pairs of triangles to quadrilateral elements in order of
their scores.
Sections 4.1 and 4.2 describe the following two
scalar functions used to score a quadrilateral,
(1) e gi for evaluating the geometric irregularity of
the i th quadrilateral, qi, formed by coupling two
adjacent triangles, and
(2) e di for evaluating the directionality error of the i
th quadrilateral, qi.
We then describe the algorithm to pair triangles in an
input mesh in Section 4.3. We also describe the
algorithm to generate a vector field from a set of input
vector values in Section 4.4. In the rest of this paper we
represent all possible quadrilaterals formed by joining
two adjacent triangular elements and the directions of
the edges of the quadrilaterals as the following ordered
lists of:
(1) quadrilaterals, Q=(q1,..., qn), and
(2) directions of the quadrilaterals’ edges, E=((e1,1,
e1,2, e1,3, e1,4),...,(en,1, en,2, en,3, en,4)).
4.1. Scalar function eeee g for measuring the geometric
irregularity of quadrilaterals
In order to measure the geometric irregularity of the i th
quadrilateral, qi, we define the following scalar function:
e gi 1
–=
2
ri
----
Ri
(6)
Here, as shown in Fig. 4, ri is the radius of the
minimum inscribed circle, the smallest circle tangent to
at least three edges of an element, and Ri is the radius
of the maximum circumcircle, the largest circle that
goes through at least three vertices of qi. The radius
ratio of the two circles, ri /Ri, takes its maximum value
1 2⁄
for a square, and minimum value 0 for a highly
irregular quadrilateral. Therefore, the value of e gi is 0 in
the best case, and 1 in the worst case.
4.2. Scalar function
eeee d for measuring the
directionality error of quadrilaterals
In order to measure the directionality error of the i th
quadrilateral, qi, we define the following scalar function:
e di
2+(
2
=
4–Ł
) 1
1
---
4
k 1=
{
}
)
,
max ei k, di
ei k, N di
-------------------------------------------------------------
ei k,
(
(7)
As also shown in Fig. 5, di denotes the unit vector
obtained from the input vector field at the center of
the quadrilateral element, and N denotes the unit
normal vector of the quadrilateral element. The value
(N di)|} takes its maximum value
max{|ei,k
1 for an edge perfectly aligned along the given vector,
and minimum value
when the edge and the
desired direction form an angle of 45 degrees. Therefore,
the value of e di is 0 in the best case, and 1 in the worst
case.
di|, |ei,k
1 2⁄
4.3. Coupling of
quadrilaterals
triangle pairs
to
form
Two previous sections defined two scalar functions,
e gi and e di, that measure the geometric irregularity and
directionality error, respectively. By taking a weighted
sum of these two functions, we define the following
metric, e i, that decides the order of coupling triangles:
e i=(1-a)e gi+ae di
0 a 1
(8)
where a is a user-defined weighting factor representing
the relative importance of the two measurements. Lower
values of a give greater importance to shape regularity than
directionality. Values of e i for all possible quadrilaterals
are first calculated in our algorithm, since they do not
change during the entire coupling process. All possible
quadrilaterals are then inserted into a list, L, and sorted
Fig. 4. Function for evaluating the geometric irregularity of a
quadrilateral.
Fig. 5. Function for evaluating the directionality error of a
quadrilateral.
·
ł
Takayuki Itoh and Kenji Shimada
Automatic Conversion of Triangular Meshes Into Quadrilateral Meshes with Directionality
Fig. 6. Pseudo code for the mesh conversion method.
by their e i values.
The quadrilaterals are then extracted from list L in
the order of their e i values. Suppose two triangles, ta
and tb, form an extracted quadrilateral, ta and tb’s other
adjacencies need to be deleted. This process is repeated
until the list L becomes empty, and finally no triangle has
an adjacency with more than one other triangular
element. Edges shared by each pair of triangles are then
deleted to form a quad-dominant mesh. The complete
procedure for the above algorithm is given in Fig. 6.
Although an output quad-dominant mesh generated
by the above algorithm still contains a small number of
triangular elements, the mesh can be converted into an
all-quadrilateral mesh by applying the templates shown
in Fig. 2.
4.4. Automated vector field generation
Although the mesh conversion algorithm described in
the previous section requires a desired mesh directionality
as a vector field, this vector field need not be provided
by the user at all, or it may be provided at only a set of
selected locations in the mesh domain. This section
describes a method for generating a vector field
automatically in these situations.
Suppose that desired mesh directionality is provided
by the user as vector values at a set of points in the
mesh domain. We denote these points and vector values
as :
(1) points, PP=(p1,...,pl), and
(2) Vector values, DP=(d1,...,dl),
where l is the number of the given points at which the
desired mesh directionality is specified.
Our implementation assigns vector values to the grid-
points of grid G to represent a vector field defined over
the entire mesh domain and well aligned along the
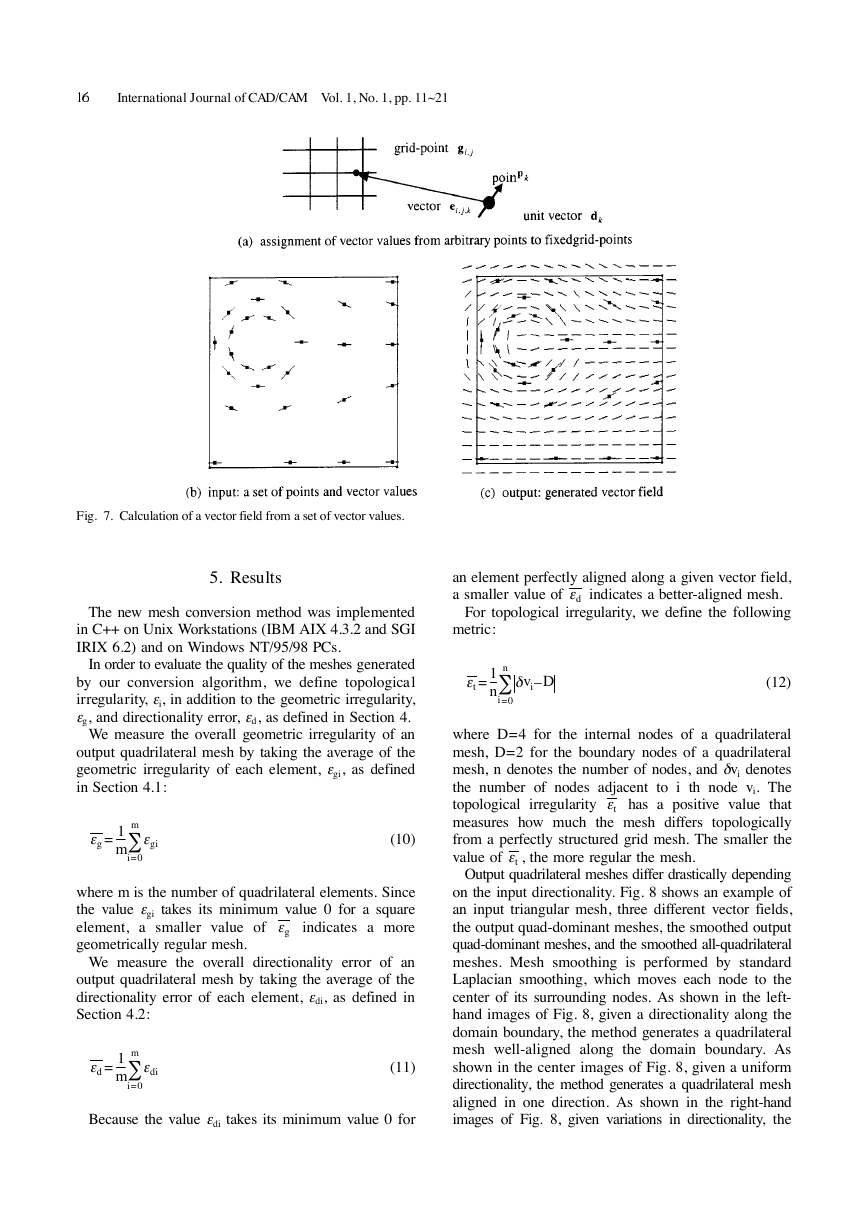
vector values Dp . We calculate a vector value, di,j, that
is the vector value at a grid-point, gi,j, of a two-
dimensional grid using the following formula:
l
=
di j,
k 1=
dk
-------------
2
ei j k, ,
(9)
where dk is the given unit vector at point pk, and ei,j,k is
the vector from point pk to grid-point gi, j as shown in
Fig. 7(a). Fig. 7(b) shows an example of a set of input
vector values, and Fig. 7(c) shows a complete vector
field calculated from the set of input vector values.
This vector averaging technique works best when the
input vectors are evenly spaced. When a region has
many input vectors clustered together, they tend to
outweigh other input vectors. This problem can be
avoided by limiting the maximum number of vectors
used in a local region.
If it is desirable that the elements be well aligned
along the domain boundary, like meshes generated by
the advancing front method, our mesh conversion method
can generate such meshes by automatically generating
a vector field along the domain boundary using the
same method described above. To generate such a vector
field we take a set of points on the domain boundary
and assign vector values at these points according to
the boundary direction.
International Journal of CAD/CAM Vol. 1, No. 1, pp. 11~21
Fig. 7. Calculation of a vector field from a set of vector values.
5. Results
The new mesh conversion method was implemented
in C++ on Unix Workstations (IBM AIX 4.3.2 and SGI
IRIX 6.2) and on Windows NT/95/98 PCs.
In order to evaluate the quality of the meshes generated
by our conversion algorithm, we define topological
irregularity, e i, in addition to the geometric irregularity,
e g, and directionality error, e d, as defined in Section 4.
We measure the overall geometric irregularity of an
output quadrilateral mesh by taking the average of the
geometric irregularity of each element, e gi, as defined
in Section 4.1:
e g
m=
1
----
m
i 0=
e gi
(10)
where m is the number of quadrilateral elements. Since
the value e gi takes its minimum value 0 for a square
element, a smaller value of
indicates a more
geometrically regular mesh.
e g
We measure the overall directionality error of an
output quadrilateral mesh by taking the average of the
directionality error of each element, e di, as defined in
Section 4.2:
e d
m=
1
----
m
i 0=
e di
(11)
Because the value e di takes its minimum value 0 for
an element perfectly aligned along a given vector field,
a smaller value of
indicates a better-aligned mesh.
e d
For topological irregularity, we define the following
metric:
e t
n=
1
---
n
i 0=
d vi D–
(12)
where D=4 for the internal nodes of a quadrilateral
mesh, D=2 for the boundary nodes of a quadrilateral
mesh, n denotes the number of nodes, and d vi denotes
the number of nodes adjacent to i th node vi. The
topological irregularity
has a positive value that
measures how much the mesh differs topologically
from a perfectly structured grid mesh. The smaller the
value of
, the more regular the mesh.
e t
e t
Output quadrilateral meshes differ drastically depending
on the input directionality. Fig. 8 shows an example of
an input triangular mesh, three different vector fields,
the output quad-dominant meshes, the smoothed output
quad-dominant meshes, and the smoothed all-quadrilateral
meshes. Mesh smoothing is performed by standard
Laplacian smoothing, which moves each node to the
center of its surrounding nodes. As shown in the left-
hand images of Fig. 8, given a directionality along the
domain boundary, the method generates a quadrilateral
mesh well-aligned along the domain boundary. As
shown in the center images of Fig. 8, given a uniform
directionality, the method generates a quadrilateral mesh
aligned in one direction. As shown in the right-hand
images of Fig. 8, given variations in directionality, the
Takayuki Itoh and Kenji Shimada
Automatic Conversion of Triangular Meshes Into Quadrilateral Meshes with Directionality
Fig. 8. Output quadrilateral meshes are well-aligned along the input mesh directionality.
method generates a quadrilateral mesh that aligns along
the various directions.
The output quadrilateral meshes also vary greatly
depending on the value of the weighting coefficient
controlling element shape regularity and directionality.
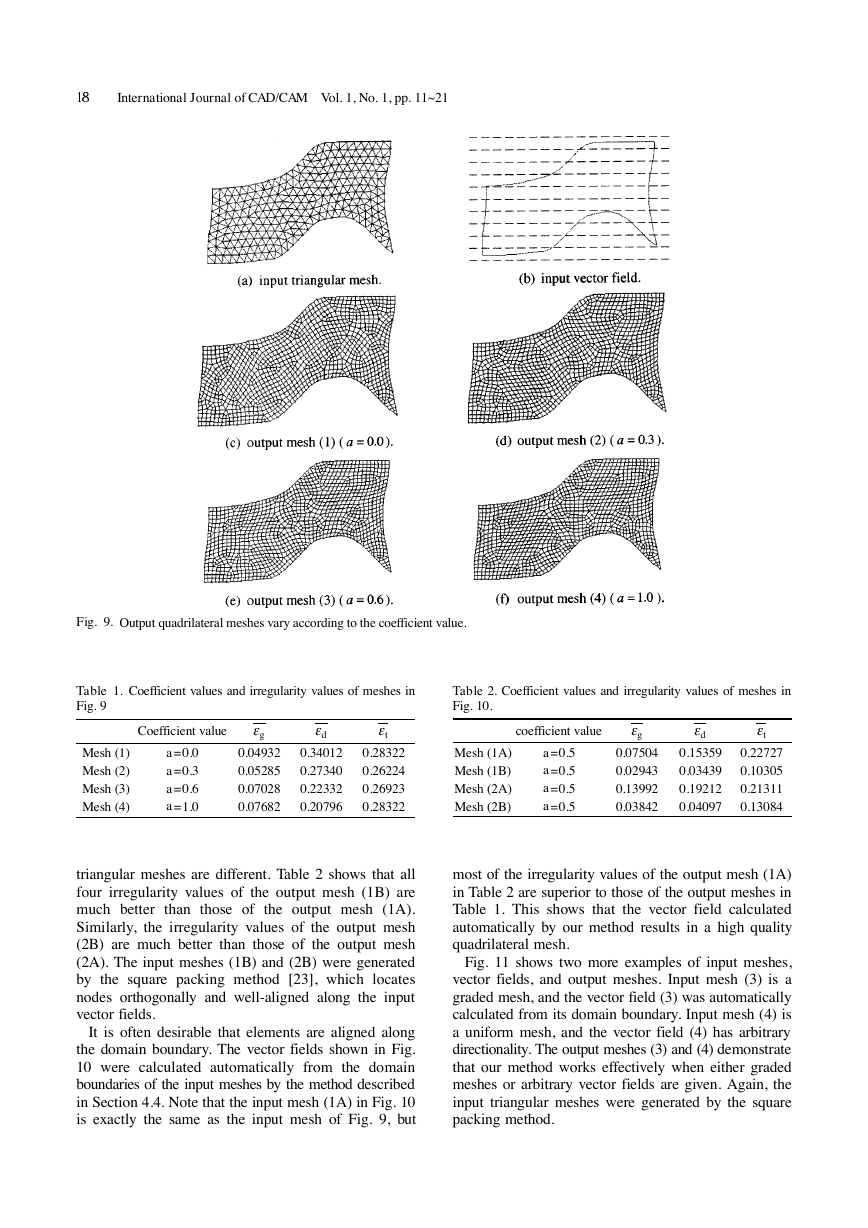
Fig. 9 shows an example of an input mesh, an input
vector field, and the different smoothed output quad-
rilateral meshes generated while varying the coefficient
value. Table 1 shows the selected coefficient values and
the resulting irregularity values. Smaller a values produce
values, denoting a well-shaped mesh.
the smaller
Larger a values result in the smaller
values, indicating
e g
e d
a well-aligned mesh.
The output quadrilateral meshes also diverge depending
on the input meshes. Fig. 10(a) and 10(b) show an
example of two input triangular meshes that have exactly
the same domain boundaries and the same vector field,
but the two smoothed output all-quadrilateral meshes
are distinct due to the different meshing patterns of the
input triangular meshes. Figs. 10(c) and 10(d) show a
similar example. Table 2 shows the irregularity values
of the output meshes. Note that the domain boundaries,
vector fields, and coefficient value are all identical
between Fig. 10(a) and Fig. 10(b). Only the input
International Journal of CAD/CAM Vol. 1, No. 1, pp. 11~21
Fig. 9. Output quadrilateral meshes vary according to the coefficient value.
Table 1. Coefficient values and irregularity values of meshes in
Fig. 9
Table 2. Coefficient values and irregularity values of meshes in
Fig. 10.
Coefficient value
Mesh (1)
Mesh (2)
Mesh (3)
Mesh (4)
a=0.0
a=0.3
a=0.6
a=1.0
e g
0.04932
0.05285
0.07028
0.07682
e d
0.34012
0.27340
0.22332
0.20796
e t
0.28322
0.26224
0.26923
0.28322
coefficient value
Mesh (1A)
Mesh (1B)
Mesh (2A)
Mesh (2B)
a=0.5
a=0.5
a=0.5
a=0.5
e g
0.07504
0.02943
0.13992
0.03842
e d
0.15359
0.03439
0.19212
0.04097
e t
0.22727
0.10305
0.21311
0.13084
triangular meshes are different. Table 2 shows that all
four irregularity values of the output mesh (1B) are
much better than those of the output mesh (1A).
Similarly, the irregularity values of the output mesh
(2B) are much better than those of the output mesh
(2A). The input meshes (1B) and (2B) were generated
by the square packing method [23], which locates
nodes orthogonally and well-aligned along the input
vector fields.
It is often desirable that elements are aligned along
the domain boundary. The vector fields shown in Fig.
10 were calculated automatically from the domain
boundaries of the input meshes by the method described
in Section 4.4. Note that the input mesh (1A) in Fig. 10
is exactly the same as the input mesh of Fig. 9, but
most of the irregularity values of the output mesh (1A)
in Table 2 are superior to those of the output meshes in
Table 1. This shows that the vector field calculated
automatically by our method results in a high quality
quadrilateral mesh.
Fig. 11 shows two more examples of input meshes,
vector fields, and output meshes. Input mesh (3) is a
graded mesh, and the vector field (3) was automatically
calculated from its domain boundary. Input mesh (4) is
a uniform mesh, and the vector field (4) has arbitrary
directionality. The output meshes (3) and (4) demonstrate
that our method works effectively when either graded
meshes or arbitrary vector fields are given. Again, the
input triangular meshes were generated by the square
packing method.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
