2006年海南省海口市中考数学真题及答案.doc-资料库

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

2006 年海南省海口市中考数学真题及答案（考试时间 100 分钟，满分 150 分，）特别提醒： 1．选择题用 2B 铅笔填涂，其余答案一律用黑色笔填写在答题卡上，写在试题卷上无效. 2．答题前请认真阅读试题及有关说明. 3．请合理安排好答题时间. 一、选择题（本大题满分 30 分，每小题 36 分） 1．计算 2-3 的结果是 A．5 B．-5 C．1 D．-1 2．今年 1 至 4 月份，我省旅游业一直保持良好的发展势头，旅游收入累计达 5163000000 元，用科学记数法表示是 A. 5163×106 元 B. 5.163×108 元 C. 5.163×109 元 D. 5.163×1010 元 3. 下列各图中，是中心对称图形的是 A  x y 4．函数 B C D 1 中，自变量 x 的取值范围是 A. 1x B. 1x C. 0x D. 1x 5．化简 8 的结果是 A．2 B．4 C． 22 D． 22 6．用配方法解方程 2 x 4  x 01  ，经过配方，得到 A． ( x )2 2  5 B． ( x )2 2  5 C． ( x )2 2  3 D． ( x )2 2  3 7．一次函数 y 2 x 的大致图象是 y O A. y O x y x O x B. C. y O D. x

8．三角形在正方形网格纸中的位置如图 1 所示，则 sinα的值是 A. 3 4 B. 4 3 C. 3 5 D. 4 5 9．下列长度的三条线段，能组成三角形的是 A．1cm，1cm，3cm B．2cm，3cm，5cm C．3cm，4cm，9cm D．5cm，6cm，8cm  图 1 10.如图 2，在菱形 ABCD 中，E、F、G、H 分别是菱形四边的中点，连结 EG 与 FH 交于点 O，则图中的菱形共有 A．4 个 B．5 个 C．6 个 D．7 个 B E F A O C 图 2 H G D C A O B D 图 3 11.如图 3，AB 和 CD 都是⊙0 的直径，∠AOC=90°，则∠C 的度数是 A．20° B．25° C．30° D．50° 12.在一次中学生田径运动会上，参加男子跳高的 15 名运动员的成绩如下表：跳高成绩(m) 1.50 1.55 1.60 1.65 1.70 1.75 跳高人数 1 3 2 3 5 1 这些运动员跳高成绩的中位数和众数分别是 A．1.65，1.70 B．1.70，1.65 C．1.70，1.70 D．3，5 二、填空题（本大题满分 24 分，每小题 3 分） 13．计算： 2 aa   3 a  14. 当 x = 时，分式 . 2 2 x 的值为零.  x  15. 今年市场上荔枝的价格比去年便宜了 5%，去年的价格是每千克 m 元，则今年的价格是每千克元. 16. 如图 4，直线 a 、b 被直线  所截，如果 a ∥b ，∠1=120°，那么∠2= 度.  1 2 图 4 a b C A D 图 5 B 图 6

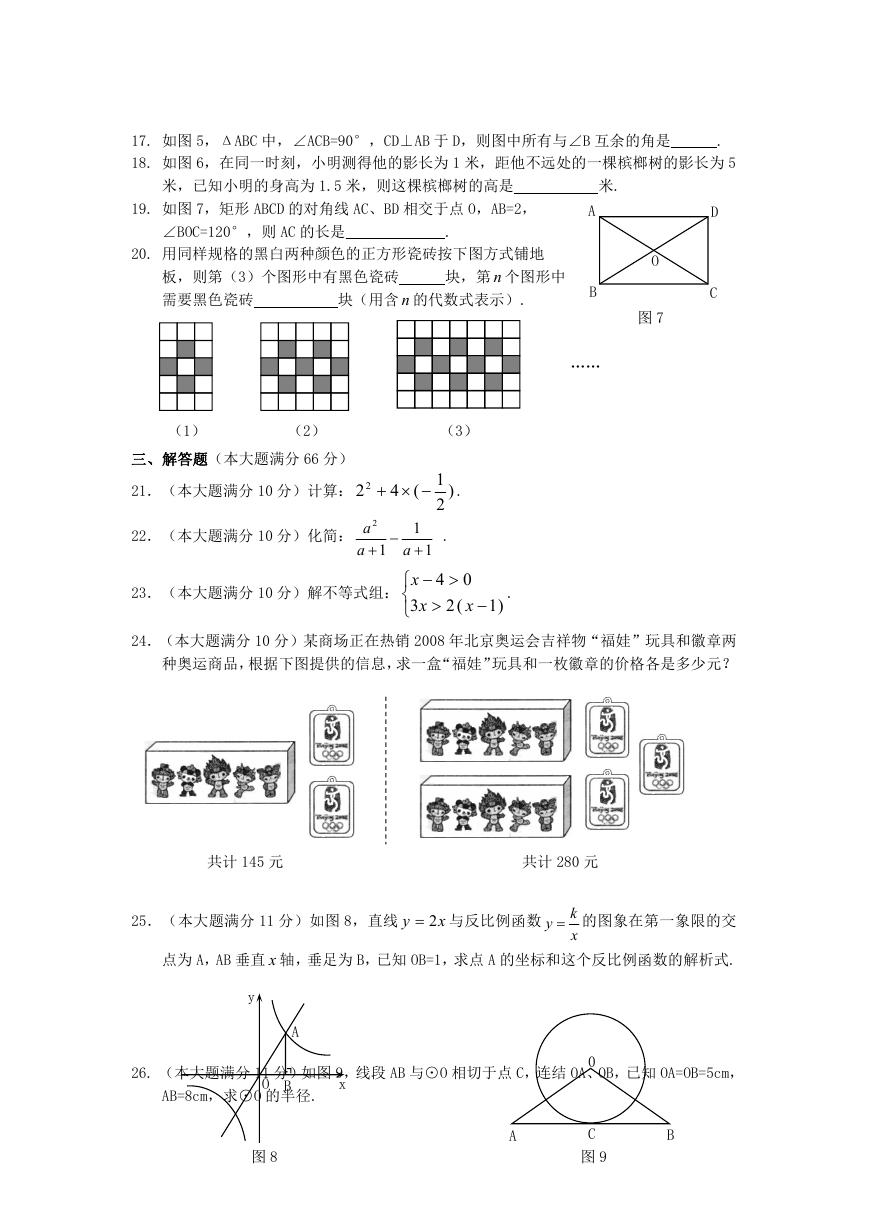
17. 如图 5，ΔABC 中，∠ACB=90°，CD⊥AB 于 D，则图中所有与∠B 互余的角是 18. 如图 6，在同一时刻，小明测得他的影长为 1 米，距他不远处的一棵槟榔树的影长为 5 . 米，已知小明的身高为 1.5 米，则这棵槟榔树的高是米. 19. 如图 7，矩形 ABCD 的对角线 AC、BD 相交于点 O，AB=2， ∠BOC=120°，则 AC 的长是 . 20. 用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板，则第（3）个图形中有黑色瓷砖需要黑色瓷砖块（用含 n 的代数式表示）. 块，第 n 个图形中 D C O 图 7 A B …… （1）（2）（3）三、解答题（本大题满分 66 分） 21．（本大题满分 10 分）计算： 22 1(4  2 ) . 22．（本大题满分 10 分）化简： 2 a a  1  23．（本大题满分 10 分）解不等式组： . 1 1 a  4 x    3 (2 x   0 x .  )1 24．（本大题满分 10 分）某商场正在热销 2008 年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品，根据下图提供的信息，求一盒“福娃”玩具和一枚徽章的价格各是多少元？共计 145 元共计 280 元 25．（本大题满分 11 分）如图 8，直线 y 2 与反比例函数 x y  的图象在第一象限的交 k x 点为 A，AB 垂直 x 轴，垂足为 B，已知 OB=1，求点 A 的坐标和这个反比例函数的解析式. y A 26. （本大题满分 11 分）如图 9，线段 AB 与⊙O 相切于点 C，连结 OA、OB，已知 OA=OB=5cm， 0 AB=8cm，求⊙O 的半径. O B x 图 8 A C 图 9 B

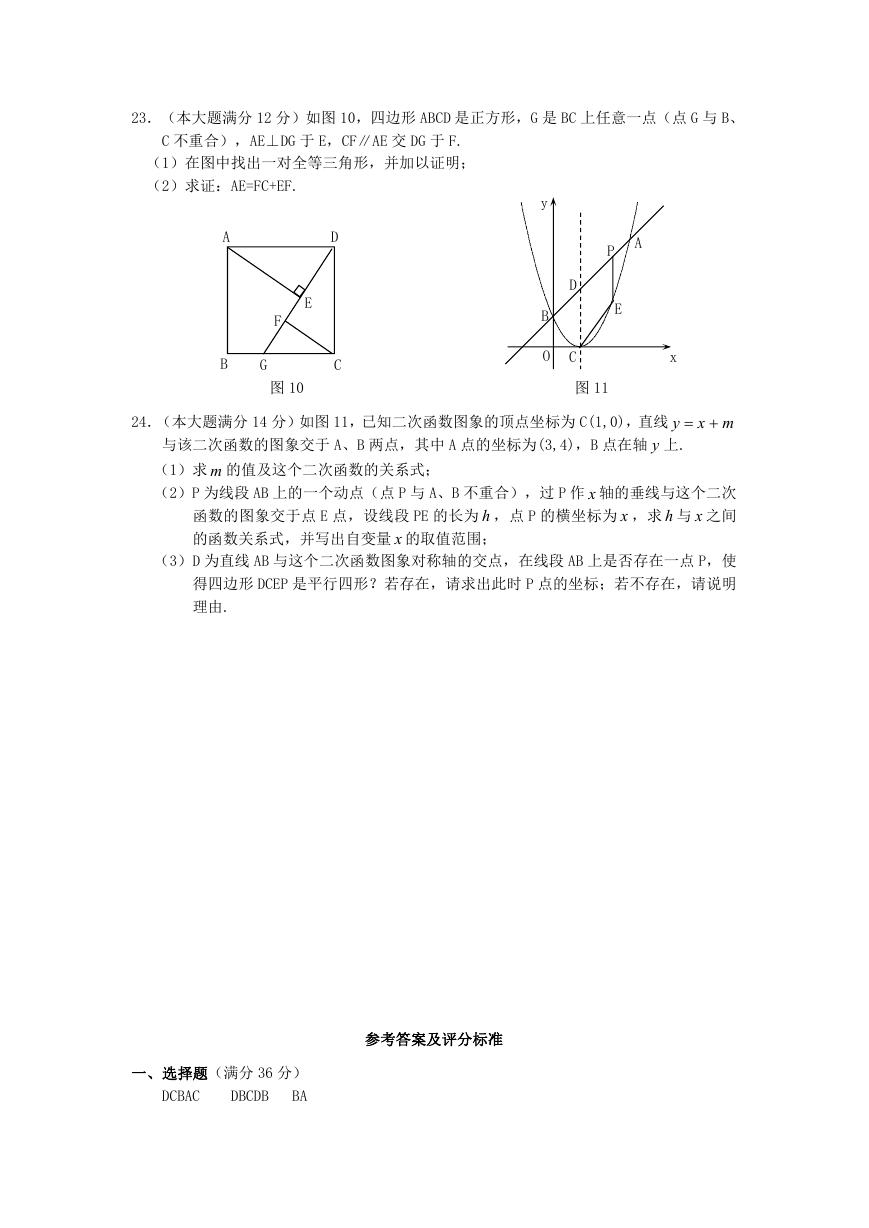
23．（本大题满分 12 分）如图 10，四边形 ABCD 是正方形，G 是 BC 上任意一点（点 G 与 B、 C 不重合），AE⊥DG 于 E，CF∥AE 交 DG 于 F. （1）在图中找出一对全等三角形，并加以证明；（2）求证：AE=FC+EF. A D E F B G C 图 10 y B O D C A P E x 图 11 24．（本大题满分 14 分）如图 11，已知二次函数图象的顶点坐标为 C(1,0)，直线 y 与该二次函数的图象交于 A、B 两点，其中 A 点的坐标为(3,4)，B 点在轴 y 上. （1）求 m 的值及这个二次函数的关系式；（2）P 为线段 AB 上的一个动点（点 P 与 A、B 不重合），过 P 作 x 轴的垂线与这个二次函数的图象交于点 E 点，设线段 PE 的长为 h ，点 P 的横坐标为 x ，求 h 与 x 之间的函数关系式，并写出自变量 x 的取值范围； mx  （3）D 为直线 AB 与这个二次函数图象对称轴的交点，在线段 AB 上是否存在一点 P，使得四边形 DCEP 是平行四形？若存在，请求出此时 P 点的坐标；若不存在，请说明理由. 参考答案及评分标准一、选择题（满分 36 分） BA DCBAC DBCDB

二、填空题（满分 24 分） 13． 32a 17. ∠A 和∠2 14. 2 18. 7.5 15. (1-5%)m 或 95%m 或 0.95m 19. 4 20. 10,3n+1 16. 60 三、解答题（满分 90 分） 21．原式=4-2 =2 22．原式  12 a  1 a  )(1 ( a a  1 a  1 a   )1 23．解不等式①，得 x＞4 ………………………………（6 分） ………………………………（10 分） ………………………………（4 分） ………………………………（6 分） ………（10 分） ………（4 分） ………（8 分） 5 解不等式②，得 x＞-2 把不等式①和②的解集在同一数轴上表示如图所示： ∴ 原不等式组的解集为 x＞4. -1 0 -2 -3 1 2 3 4 ………………………………（10 分） 24. 设一盒“福娃”玩具和一枚徽章的价格分别为 x 元和 y 元. …………………（1 分）依题意，得 x 2    解这个方程组，得 145 2 y   3 280 y x   125 x    10 y   ………………………………（6 分） ………………………………（9 分）答：一盒“福娃”玩具和一枚徽章的价格分别为 125 元和 10 元. ……………（10 分）（注：其他解法仿照以上评分标准.） 25．∵ AB 垂直 x 轴于点 B，OB=1，且点 A 在第一象限， ∴ 点 A 的横坐为 1. 又∵ 直线 y=2x 的图象过点 A， ∴ y=2x=2×1=2. 即点 A 的坐标为(1,2). ………………………………（2 分） ………………………………（4 分） ………………………………（6 分） ∵ k y  的图象过点 A(1,2), x k 1 ∴ k=2. ∴ 2 . ∴ 这个反比例函数的解析式为 y 2 x . 26. 连结 OC. ∵ AB 与⊙O 相切于点 C， ∴ OC⊥AB. 又∵ OA=OB， ∴ AC=BC= 1 AB= 2 1 2 OC  ∴⊙O 的半径为 3cm. 在 RtΔAOC 中，  48 （cm）. A 2 OA  2 AC  2 5  2 4  3 （cm）. 27. (1) ΔAED≌ΔDFC. ∵ 四边形 ABCD 是正方形, ∴ AD=DC，∠ADC=90º. 又∵ AE⊥DG，CF∥AE， ………………………………（8 分） ………………………………（10 分） ………………………………（11 分） 0 C ……………（1 分） ……………（5 分） B ………（8 分） ……………（11 分） ………………………………（2 分） ………………………………（4 分）

∴ ∠AED=∠DFC=90º, ∴ ∠EAD+∠ADE=∠FDC+∠ADE=90º， ∴ ∠EAD=∠FDC. ∴ ΔAED≌ΔDFC （AAS）. ………………………………（5 分） ………………………………（7 分） ………………………………（9 分） (2) ∵ ΔAED≌ΔDFC， ∴ AE=DF，ED=FC. ∵ DF=DE+EF， ∴ AE=FC+EF. 28. (1) ∵ 点 A(3,4)在直线 y=x+m 上， ………………………………（12 分） ………………………………（14 分） ∴ 4=3+m. ∴ m=1. 设所求二次函数的关系式为 y=a(x-1)2. ∵ 点 A(3,4)在二次函数 y=a(x-1)2 的图象上， ∴ 4=a(3-1)2, ∴ a=1. ∴ 所求二次函数的关系式为 y=(x-1)2. 即 y=x2-2x+1. ………………………………（1 分） ………………………………（2 分） ………………………………（3 分） ………………………………（4 分） ………………（5 分） (2) 设 P、E 两点的纵坐标分别为 yP 和 yE . 即 h=-x2+3x (0＜x＜3). (3) 存在. ∴ PE=h=yP-yE =(x+1)-(x2-2x+1) =-x2+3x. ………………………………（6 分） ………………………………（7 分） ………………………………（8 分） ………………………………（9 分） ………………………………（10 分）解法 1：要使四边形 DCEP 是平行四边形，必需有 PE=DC. ………………（11 分） ∵ 点 D 在直线 y=x+1 上, ∴ 点 D 的坐标为(1,2), ∴ -x2+3x=2 . 即 x2-3x+2=0 . ………………………………（12 分） ………………………………（13 分）解之，得 x1=2，x2=1 (不合题意，舍去) ∴ 当 P 点的坐标为(2,3)时，四边形 DCEP 是平行四边形. ……………（14 分）解法 2：要使四边形 DCEP 是平行四边形，必需有 BP∥CE. ………………（11 分）设直线 CE 的函数关系式为 y=x+b. ∵ 直线 CE 经过点 C(1,0), ∴ 0=1+b, ∴ b=-1 . ∴ 直线 CE 的函数关系式为 y=x-1 . ∴ y y     2  x x 1  2 x  1 得 x2-3x+2=0. ………………………………（12 分）解之，得 x1=2，x2=1 (不合题意，舍去) ………………………………（13 分） ∴ 当 P 点的坐标为(2,3)时，四边形 DCEP 是平行四边形. ……………（14 分）

资料库

2006年海南省海口市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料