论文研究-基于变形蔡氏电路的混沌保密通信电路研究 .pdf-资料库

weixin_39840515-11575405-4744300845378894437.pdf-第1页.png

第1页 / 共14页

weixin_39840515-11575405-4744300845378894437.pdf-第2页.png

第2页 / 共14页

weixin_39840515-11575405-4744300845378894437.pdf-第3页.png

第3页 / 共14页

weixin_39840515-11575405-4744300845378894437.pdf-第4页.png

第4页 / 共14页

weixin_39840515-11575405-4744300845378894437.pdf-第5页.png

第5页 / 共14页

weixin_39840515-11575405-4744300845378894437.pdf-第6页.png

第6页 / 共14页

weixin_39840515-11575405-4744300845378894437.pdf-第7页.png

第7页 / 共14页

weixin_39840515-11575405-4744300845378894437.pdf-第8页.png

第8页 / 共14页

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 基于变形蔡氏电路的混沌保密通信电路研究盛新庆* （北京邮电大学信息与通信工程学院，北京 100876）摘要：分析用三次多项式代替蔡氏电路状态方程组中的分段线性函数，得到的新的状态方程组能产生混沌信号。根据变形的微分方程组，用更优化的模块化电路实现蔡氏电路，此模块化电路用三个积分器、两个加法器和两个乘法器即可实现。用该电路产生的混沌信号去掩盖和解调低频信号，可实现通信的保密。根据电路的电流流向，用易于实现且实验技术上可行的耦合同步法实现发送端和接受端的同步。对所设计电路用 Matlab 进行了全面仿真，包括性能仿真、误差仿真、失真仿真等,仿真结果与理论分析十分吻合，结果表明所设计的电路不仅保密性能良好，而且灵活性很强。关键词：混沌保密通信；变形蔡氏电路；模块化；仿真中图分类号：TN918.6+4 Chaotic Secure Communication Base on Modified Chua's Circuit Sheng Xinqing (School of Information and Communication Engineering of BUPT, Beijing 100876) Abstract: This paper puts forward a modified Chua ’s circuit by using polynomial to replace picewise function of originalChua’s circuit. According to the new state equations, a optimized circuit which can produce chaltic signal was designed. This circuit only has two summing units,two adding units and three integral modules .Using chaltic signal produced by this circuit to cover and demodulate low frequency signal can achieve signal security. According to the current flow of the circuit,use coupled synchronization to relize the synchronization of two Chua ’s circuit. Simulation the circuit on Matlab.Simulation results indictes that the security performance of the circuit is very good. Key words: secure communication; modified Chua’s circuit; modularity; simulation 0 引言混沌是一种貌似无规则的运动，是指在确定的非线性系统中，不需要加任何随机因素亦可出现类似随机的行为(内在随机行为)。混沌现象无处不有，大至宇宙，小至微粒子，无不受混沌理论支配[1]。上世纪 70 年代，人们开始重视混沌现象，并逐渐成为一门新兴科学。 1983 年，美国贝克莱(Berkeley)大学的蔡少棠教授(Leon. o. Chua)发明了蔡氏电路(Chua' sCircuit)[2]，蔡氏电路因其简洁性和代表性而成为研究非线性电路中混沌的典范[3]。上世纪 90 年代，美国的海军实验室的学者 Pecora 和 Carroll 提出混沌同步原理[4]，拉开了混沌同步研究的序幕。混沌同步的实现为混沌用于保密通信提供了可能。在利用同步混沌进行保密通信的研究方面,迄今为止已经提出和发展了三大保密技术:混沌掩盖、混沌调制和混沌键控三种技术[5]。本文对能产生混沌信号的蔡氏电路的状态方程组进行变形，得到一组新的状态方程组。然后根据此状态方程组，设计出一种优化的模块化蔡氏电路。在发送端用该电路产生的混沌信号掩盖低频信号，在接收端用同样的电路进行解调，根据电流流向实现耦合同步。并用 Matlab 进行仿真，通过仿真可以发现，该电路保密效果良好。作者简介：盛新庆（出生 1986-），男，主要研究方向：短距离无线通信. E-mail: shengxinqing@163.com - 1 -

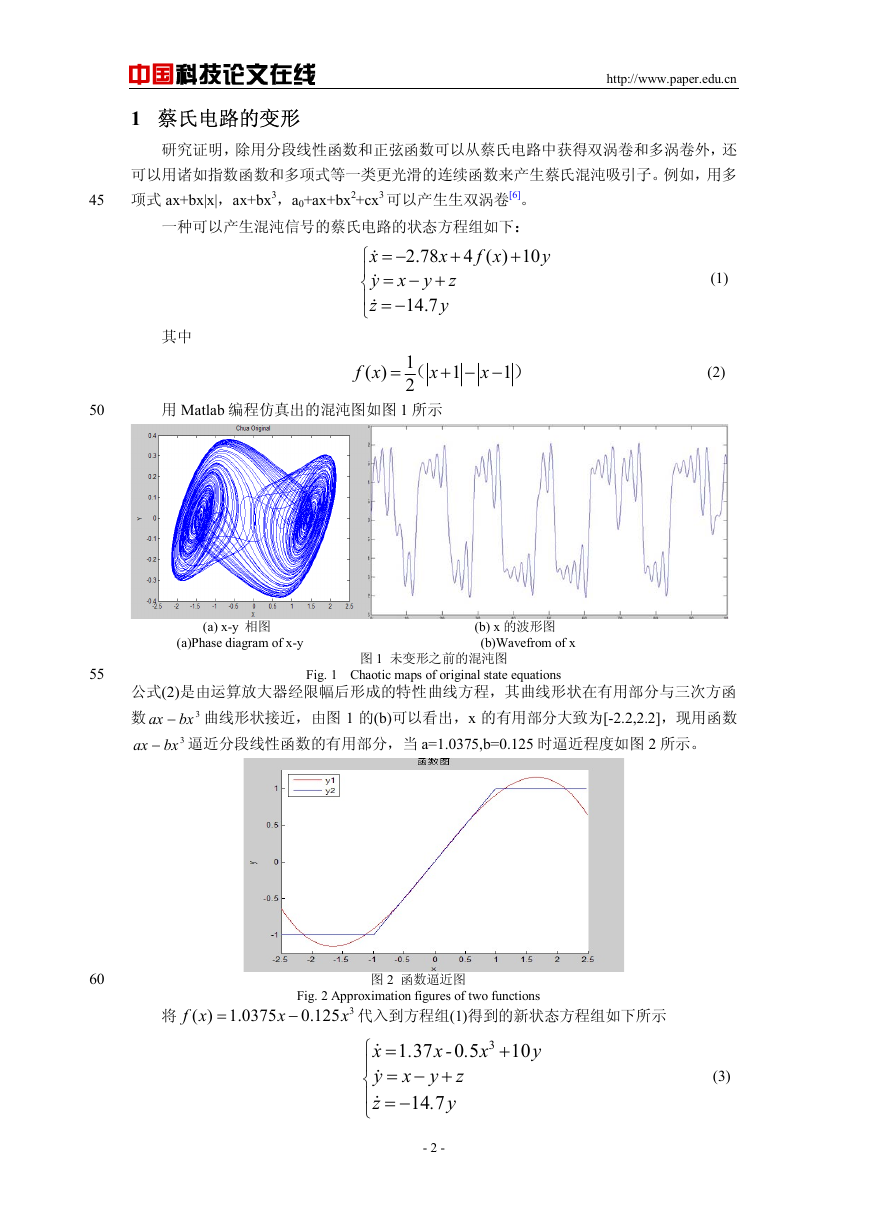
中国科技论文在线 1 蔡氏电路的变形 http://www.paper.edu.cn 研究证明，除用分段线性函数和正弦函数可以从蔡氏电路中获得双涡卷和多涡卷外，还 45 可以用诸如指数函数和多项式等一类更光滑的连续函数来产生蔡氏混沌吸引子。例如，用多项式 ax+bx|x|，ax+bx3，a0+ax+bx2+cx3 可以产生生双涡卷[6]。一种可以产生混沌信号的蔡氏电路的状态方程组如下： 4 ( ) 10 f x y + (1) x y z ⎧ ⎪ ⎨ ⎪ ⎩ + z x 2.78 = − x y = − + y 14.7 = − 其中 50 用 Matlab 编程仿真出的混沌图如图 1 所示 f x ( ) = 1 （ 2 x 1 + − − x 1 ） (2) 55 60 (a) x-y 相图 (b) x 的波形图 (a)Phase diagram of x-y (b)Wavefrom of x 图 1 未变形之前的混沌图 Fig. 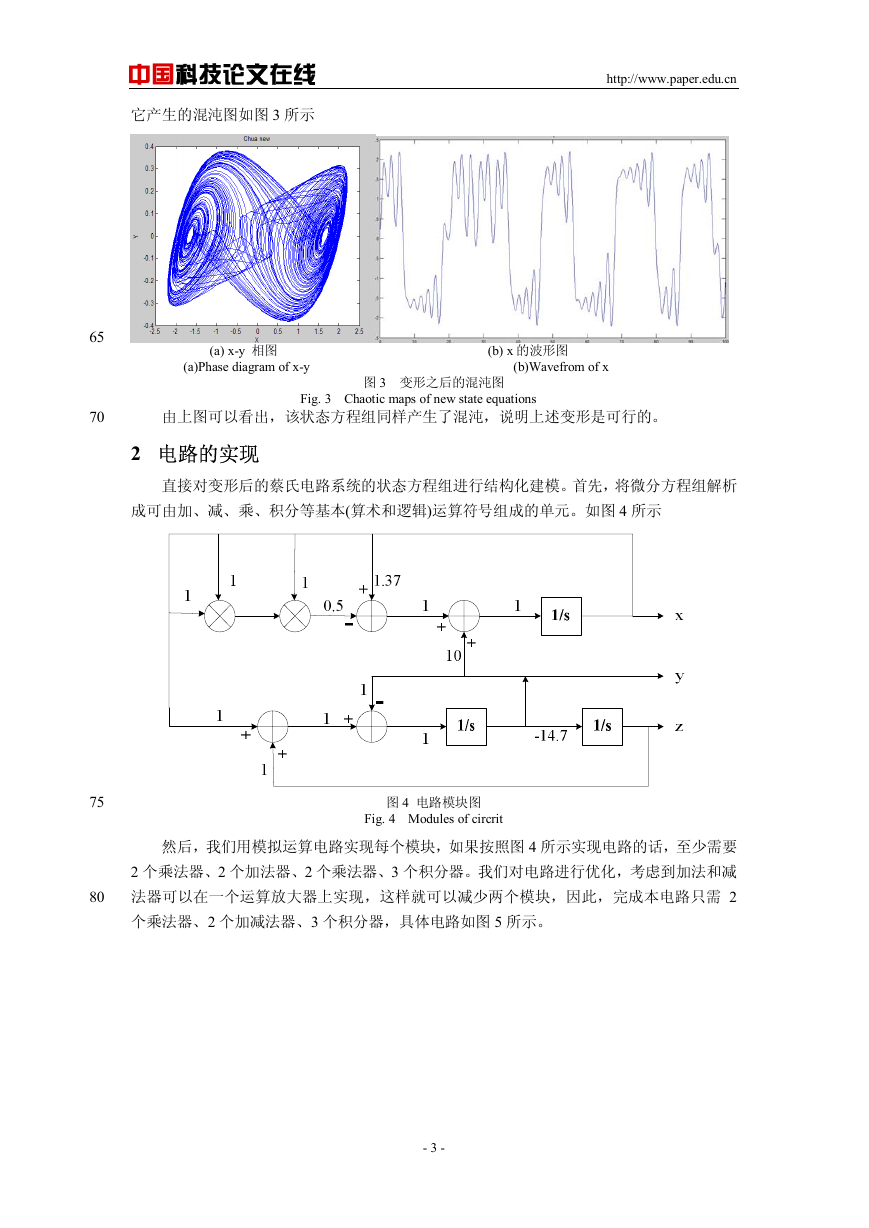1 Chaotic maps of original state equations 公式(2)是由运算放大器经限幅后形成的特性曲线方程，其曲线形状在有用部分与三次方函 ax − 曲线形状接近，由图 1 的(b)可以看出，x 的有用部分大致为[-2.2,2.2]，现用函数数 ax − 逼近分段线性函数的有用部分，当 a=1.0375,b=0.125 时逼近程度如图 2 所示。 3bx 3bx 将 f x ( ) 1.0375 = x Fig. 2 Approximation figures of two functions 0.125 − 代入到方程组(1)得到的新状态方程组如下所示 x 3 图 2 函数逼近图 3 + 10 y x y z ⎧ ⎪ ⎨ ⎪ ⎩ x - . x . 0 5 1 37 = x z y = − + . y 14 7 = − - 2 - (3)

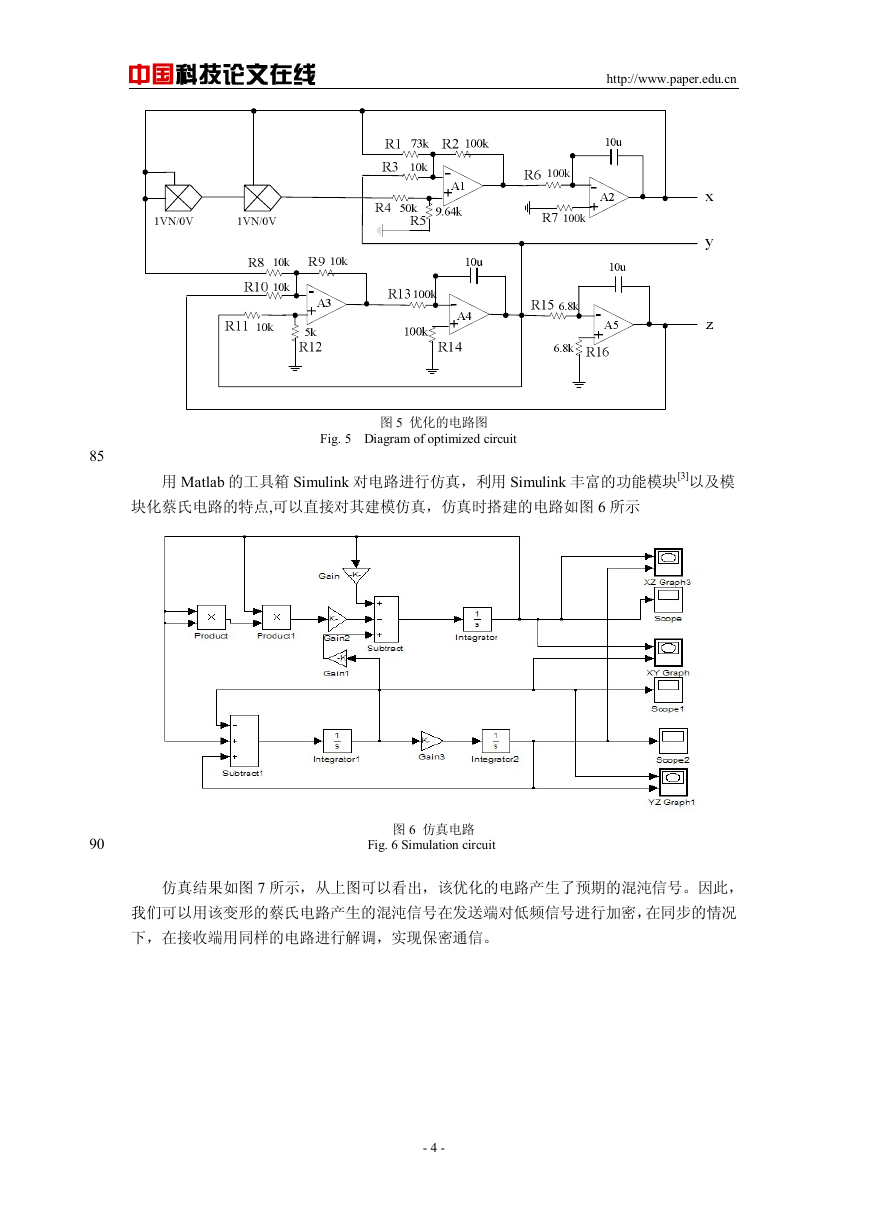
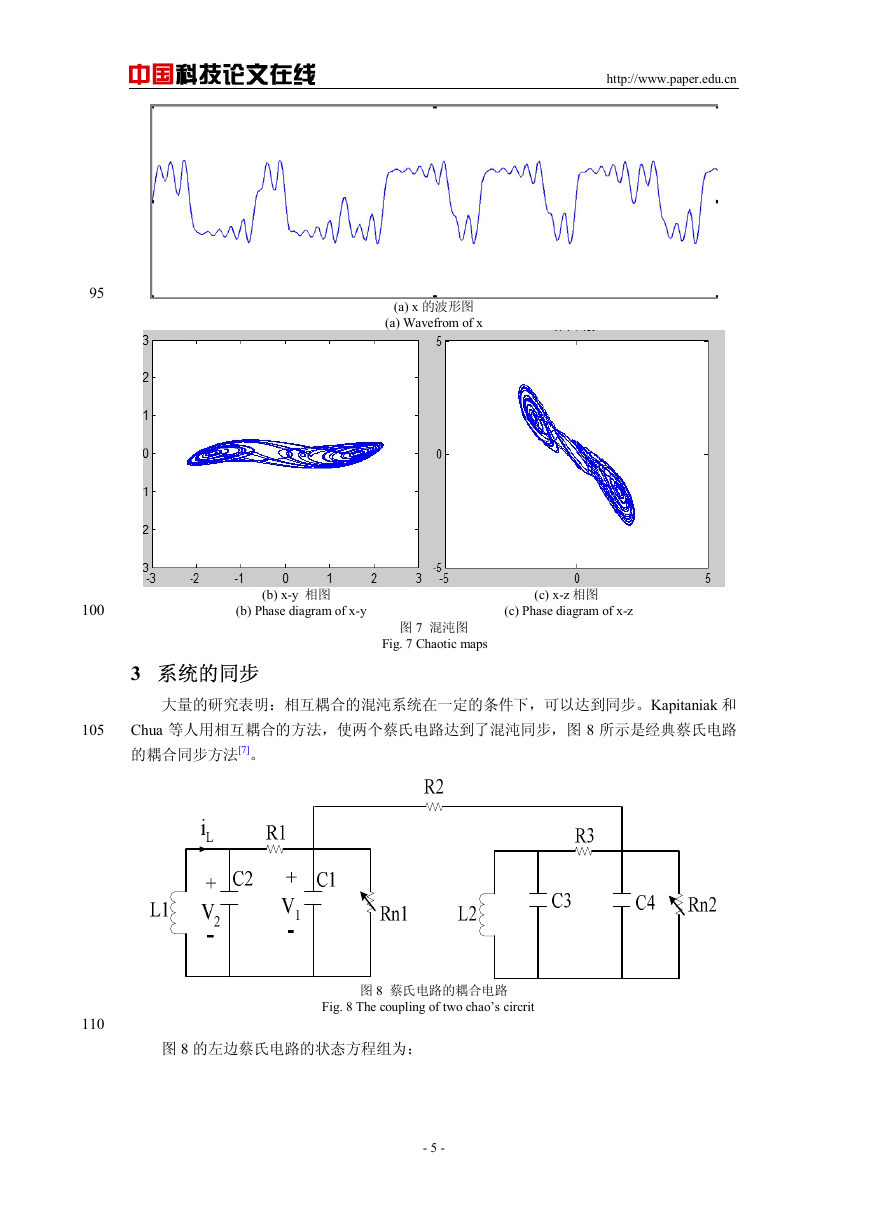
中国科技论文在线它产生的混沌图如图 3 所示 http://www.paper.edu.cn 65 70 75 80 (a) x-y 相图 (b) x 的波形图 (a)Phase diagram of x-y (b)Wavefrom of x 图 3 变形之后的混沌图 Fig. 3 Chaotic maps of new state equations 由上图可以看出，该状态方程组同样产生了混沌，说明上述变形是可行的。 2 电路的实现直接对变形后的蔡氏电路系统的状态方程组进行结构化建模。首先，将微分方程组解析成可由加、减、乘、积分等基本(算术和逻辑)运算符号组成的单元。如图 4 所示图 4 电路模块图 Fig. 4 Modules of circrit 然后，我们用模拟运算电路实现每个模块，如果按照图 4 所示实现电路的话，至少需要 2 个乘法器、2 个加法器、2 个乘法器、3 个积分器。我们对电路进行优化，考虑到加法和减法器可以在一个运算放大器上实现，这样就可以减少两个模块，因此，完成本电路只需 2 个乘法器、2 个加减法器、3 个积分器，具体电路如图 5 所示。 - 3 -

中国科技论文在线 http://www.paper.edu.cn 85 90 图 5 优化的电路图 Fig. 5 Diagram of optimized circuit 用 Matlab 的工具箱 Simulink 对电路进行仿真，利用 Simulink 丰富的功能模块[3]以及模块化蔡氏电路的特点,可以直接对其建模仿真，仿真时搭建的电路如图 6 所示图 6 仿真电路 Fig. 6 Simulation circuit 仿真结果如图 7 所示，从上图可以看出，该优化的电路产生了预期的混沌信号。因此，我们可以用该变形的蔡氏电路产生的混沌信号在发送端对低频信号进行加密，在同步的情况下，在接收端用同样的电路进行解调，实现保密通信。 - 4 -

中国科技论文在线 http://www.paper.edu.cn 95 100 105 (a) x 的波形图 (a) Wavefrom of x (b) x-y 相图 (c) x-z 相图 (b) Phase diagram of x-y (c) Phase diagram of x-z 图 7 混沌图 Fig. 7 Chaotic maps 3 系统的同步大量的研究表明：相互耦合的混沌系统在一定的条件下，可以达到同步。Kapitaniak 和 Chua 等人用相互耦合的方法，使两个蔡氏电路达到了混沌同步，图 8 所示是经典蔡氏电路的耦合同步方法[7]。 110 图 8 蔡氏电路的耦合电路 Fig. 8 The coupling of two chao’s circrit 图 8 的左边蔡氏电路的状态方程组为： - 5 -

中国科技论文在线 http://www.paper.edu.cn 1 = dVC 1 dt dV 2 C dt diL L dt 1 R 1 R V = − 2 = 2 ⎧ ⎪ ⎪ ⎪⎪ ⎨ ⎪ ⎪ ⎪ ⎪⎩ 右边蔡氏电路的状态方程组为： 1 = dVC ′ 1 dt dV ′ 2 C dt diL ′ L dt 1 R 1 R V ′ = − 2 = 2 ⎧ ⎪ ⎪ ⎪⎪ ⎨ ⎪ ⎪ ⎪ ⎪⎩ V ( 2 − V 1 ) − g V ( 1 ) + V V ′− 1 1 C R 1 V ( 2 − V 1 ) + i L (4) V ( ′ 2 − V ) ′ 1 − g V ) ( ′ 1 + V V ′− 1 1 C R 1 V ( ′ 2 − V ) ′ 1 + i ′ L (5) 115 相互耦合时第一个 n 唯非线性系统为： = X f X r ( , ) (6) 另一 n 维系统为：可以证明，如果误差函数 E = 合的混沌系统可以实现同步[8]。 120 f Y r ( , ) ′= Y f Y r ( , ) ′ − f X r , ) ( (7) 的 Jacabi 行列式特征值小于 0，两个耦研究表明:通常只需将电路中的一个状态变量适当耦合，两个相同蔡氏电路之间的同步就有可能建立[8]。 125 130 原蔡氏电路的耦合同步方法同样适用于本变形的蔡氏电路。现分析方程(3)或图 5 电路原理图中三个变量 x、y、z 的信号流向,根据电流流向实现耦合同步。x 的输入有 3 路，分别是来自 x 输出本身直接进入 x 输入，来自 x 输出本身经过非线性处理得到 x3 的一路，来自 y 输出的一路，对应于公式 (3)的第 1 式子的 3 项，并对应于图 5 的运算放大器 A1 前的三路，这三路分别与电阻 R1、R4、R3 连接；x 的输出也有 3 路，第 1 路直接与 x 输入连接，第 2 路经非线性处理得到 x3，再与 x 输入连接，第三路是与 y 的输入相连接，对应于公式 (3) 的第 1 个式子的前 2 项和第 2 个式子的第 1 项，对应于图 5，第一路是放大器 A1 前与 R1 连接的一路，第二路对应于与乘法器连接的一路，第三路对应于放大器 A3 前与 R8 连接的一路。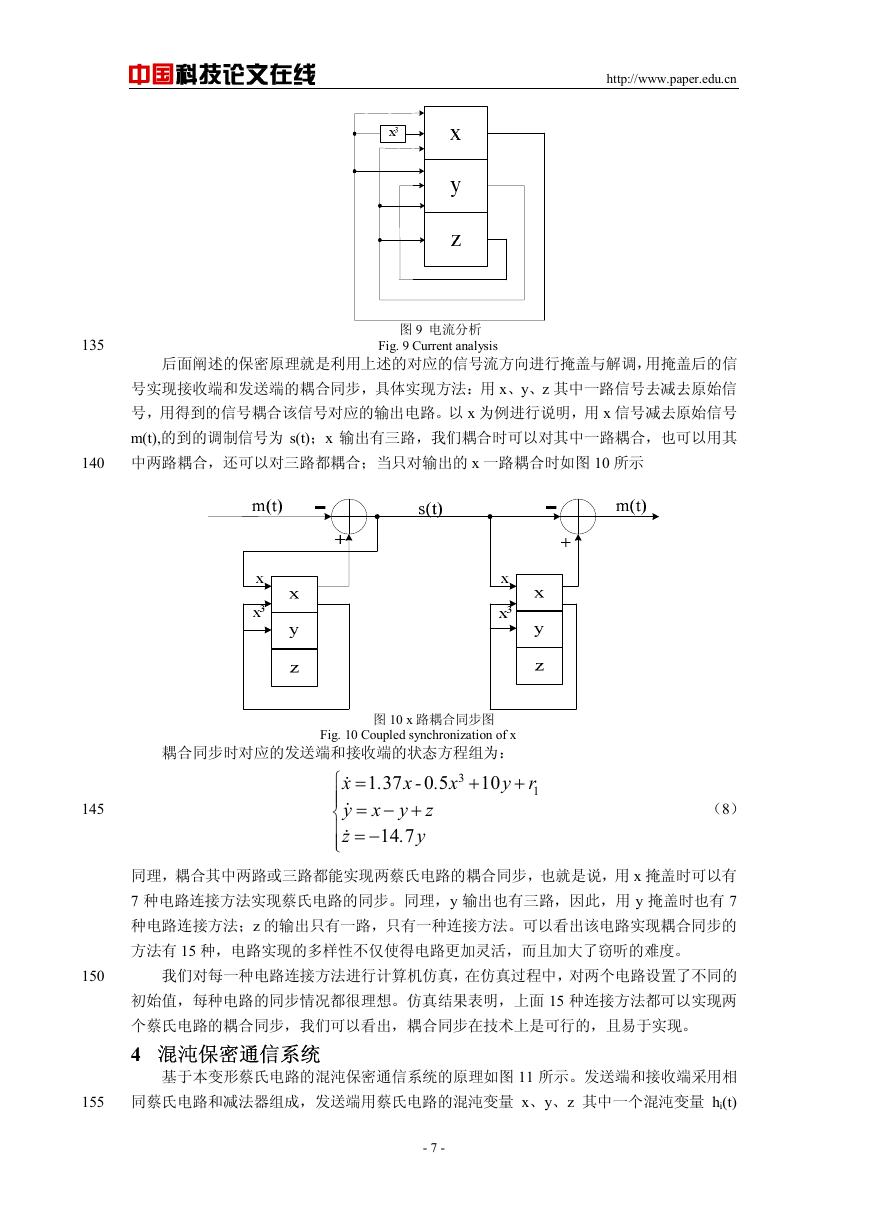对于 y 路与 z 路也存在这样的关系，y 路有 3 路输出 3 路输入,z 路仅有 1 路输出 1 路输入，共计 7 路信号流向，如图 9 所示。 - 6 -

中国科技论文在线 http://www.paper.edu.cn 图 9 电流分析 Fig. 9 Current analysis 后面阐述的保密原理就是利用上述的对应的信号流方向进行掩盖与解调，用掩盖后的信号实现接收端和发送端的耦合同步，具体实现方法：用 x、y、z 其中一路信号去减去原始信号，用得到的信号耦合该信号对应的输出电路。以 x 为例进行说明，用 x 信号减去原始信号 m(t),的到的调制信号为 s(t)；x 输出有三路，我们耦合时可以对其中一路耦合，也可以用其中两路耦合，还可以对三路都耦合；当只对输出的 x 一路耦合时如图 10 所示图 10 x 路耦合同步图 Fig. 10 Coupled synchronization of x 耦合同步时对应的发送端和接收端的状态方程组为： y + 10 3 + x - . x . 0 5 1 37 = z y x = − + . y 14 7 = − x y z ⎧ ⎪⎪ ⎨ ⎪ ⎪⎩ r 1 （8）同理，耦合其中两路或三路都能实现两蔡氏电路的耦合同步，也就是说，用 x 掩盖时可以有 7 种电路连接方法实现蔡氏电路的同步。同理，y 输出也有三路，因此，用 y 掩盖时也有 7 种电路连接方法；z 的输出只有一路，只有一种连接方法。可以看出该电路实现耦合同步的方法有 15 种，电路实现的多样性不仅使得电路更加灵活，而且加大了窃听的难度。我们对每一种电路连接方法进行计算机仿真，在仿真过程中，对两个电路设置了不同的初始值，每种电路的同步情况都很理想。仿真结果表明，上面 15 种连接方法都可以实现两个蔡氏电路的耦合同步，我们可以看出，耦合同步在技术上是可行的，且易于实现。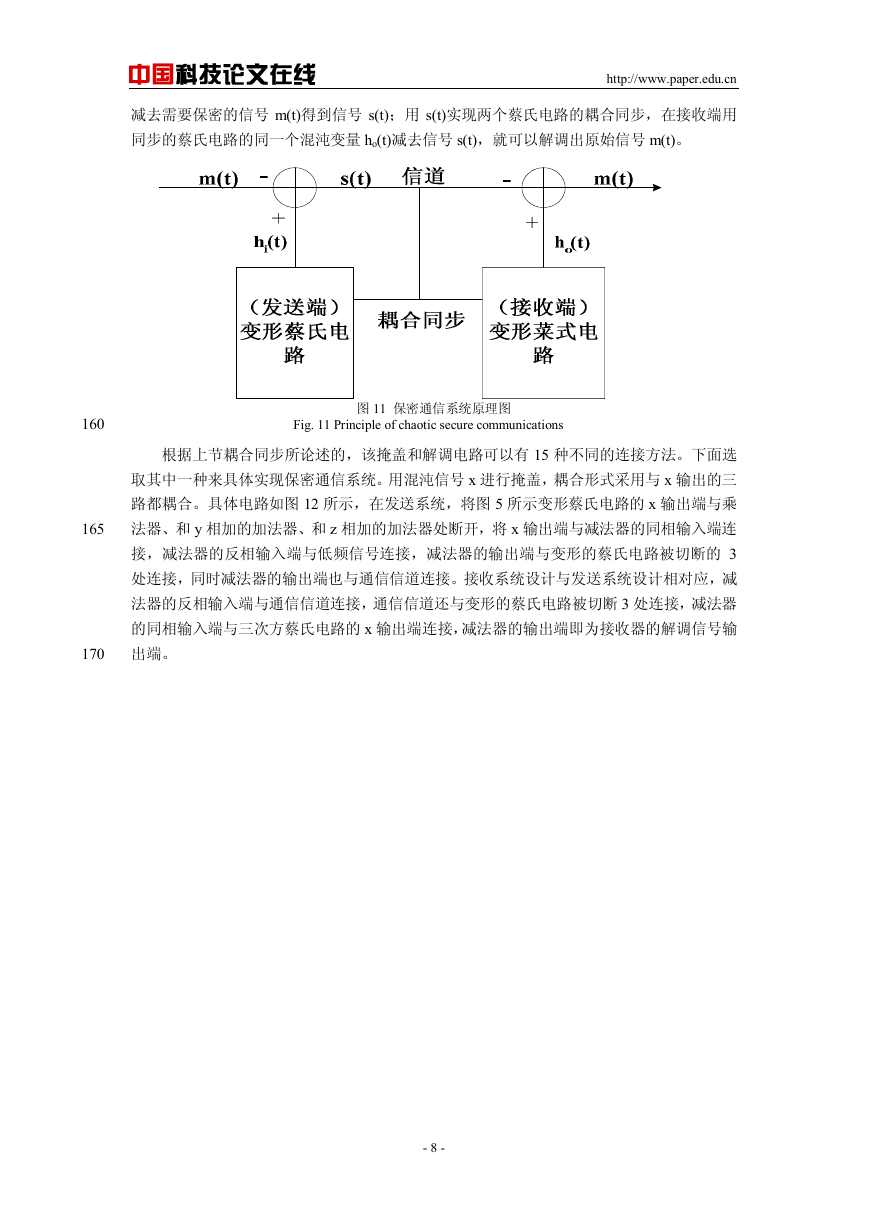 4 混沌保密通信系统基于本变形蔡氏电路的混沌保密通信系统的原理如图 11 所示。发送端和接收端采用相同蔡氏电路和减法器组成，发送端用蔡氏电路的混沌变量 x、y、z 其中一个混沌变量 hi(t) - 7 - 135 140 145 150 155

中国科技论文在线 http://www.paper.edu.cn 减去需要保密的信号 m(t)得到信号 s(t)；用 s(t)实现两个蔡氏电路的耦合同步，在接收端用同步的蔡氏电路的同一个混沌变量 ho(t)减去信号 s(t)，就可以解调出原始信号 m(t)。 160 图 11 保密通信系统原理图 Fig. 11 Principle of chaotic secure communications 根据上节耦合同步所论述的，该掩盖和解调电路可以有 15 种不同的连接方法。下面选取其中一种来具体实现保密通信系统。用混沌信号 x 进行掩盖，耦合形式采用与 x 输出的三路都耦合。具体电路如图 12 所示，在发送系统，将图 5 所示变形蔡氏电路的 x 输出端与乘法器、和 y 相加的加法器、和 z 相加的加法器处断开，将 x 输出端与减法器的同相输入端连接，减法器的反相输入端与低频信号连接，减法器的输出端与变形的蔡氏电路被切断的 3 处连接，同时减法器的输出端也与通信信道连接。接收系统设计与发送系统设计相对应，减法器的反相输入端与通信信道连接，通信信道还与变形的蔡氏电路被切断 3 处连接，减法器的同相输入端与三次方蔡氏电路的 x 输出端连接，减法器的输出端即为接收器的解调信号输出端。 165 170 - 8 -

资料库

论文研究-基于变形蔡氏电路的混沌保密通信电路研究 .pdf

相关推荐

开发技术

热门标签

最新资料