logo资料库

ABAQUS拓扑优化分析手册用户手册.pdf

发布时间：2022-06-03 发布人：admin 分类：说明书 资料大小：0.25M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    ABAQUS 拓扑优化分析手册/用户手册 分析手册： 13. Optimization Techniques 优化技术 13.1  结构优化：概述 13.1.1  概述 ABAQUS 结构优化是一个帮助用户精细化设计的迭代模块。结构优化设计能够使得结构 组件轻量化，并满足刚度和耐久性要求。ABAQUS 提供了两种优化方法——拓扑优化和形状 优化。拓扑优化（Topology optimization）通过分析过程中不断修改最初模型中指定优化区 域的单元材料性质，有效地从分析的模型中移走/增加单元而获得最优的设计目标。形状优 化（Shape optimization）则是在分析中对指定的优化区域不断移动表面节点从而达到减小局 部应力集中的优化目标。拓扑优化和形状优化均遵从一系列优化目标和约束。 最优化方法（Optimization）是一个通过自动化程序增加设计者在经验和直觉从而缩短 研发过程的工具。想要优化模型，必须知道如何去优化，仅仅说要减小应力或者增大特征值 是不够，做优化必须有更专门的描述。比方说，想要降低在两种不同载荷工况下的最大节点 力，类似的还有，想要最大化前五阶特征值之和。这种最优化的目标称之为目标函数（Object  Function）  。另外，在优化过程中可以同时强制限定某些状态参量。例如，可以指定某节点 的位移不超过一定的数值。这些强制性的指定措施叫做约束（Constraint）。 ABAQUS/CAE可以创建模型然后定义、配置和执行结构优化。更多信息请参考用户手册 第十八章。 13.1.2  术语（Terminology） 设计区域（Design area）:  设计区域即模型需要优化的区域。这个区域可以是整个模型， 也可以是模型的一部分或者数部分。一定的边界条件、载荷及人为约束下，拓扑优化通过增 加/删除区域中单元的材料达到最优化设计，而形状优化通过移动区域内节点来达到优化的 目的。 设计变量（Design variables）：设计变量即优化设计中需要改变的参数。拓扑优化中， 设计区域中单元密度是设计变量，ABAQUS/CAE 优化分析模块在其优化迭代过程中改变单元 密度并将其耦合到刚度矩阵之中。实际上，拓扑优化将模型中单元移除的方法是将单元的质 量和刚度充分变小从而使其不再参与整体结构响应。对于形状优化而言，设计变量是指设计 区域内表面节点位移。优化时，ABAQUS 或者将节点位置向外移动或者向内移动，抑或不移 动。在此过程中，约束会影响表面节点移动的多少及其方向。优化仅仅直接修改边缘处的节 点，而边缘内侧的节点位移通过边缘处节点插值得到。 设计循环（Design cycle）: 优化分析是一种不断更新设计变量的迭代过程，执行 ABAQUS 进行模型修改、查看结果以及确定是否达到优化目的。 其中每次迭代叫做一个设计循环。
    优化任务（Optimization task）： 一次优化任务包含优化的定义，比如设计响应、目标、 限制条件和几何约束。 设计响应（Design responses）: 优化分析的输入量称之为设计响应。设计响应可以直 接从 ABAQUS 的结果输出文件.odb 中读取，比如刚度、应力、特征频率及位移等。或者 ABAQUS 从结果文件中计算得到模型的设计响应，例如质心、重量、相对位移等。一个设计响应与模 型紧密相关，然而，设计响应存在一定的范围，例如区域内的最大应力或者模型体积。另外， 设计响应也与特点的分析步和载荷状况有关。 目标函数（Objective functions）: 目标函数决定了优化的目标。一个目标函数是从设 计响应中萃取的一定范围内的值，如最大位移和最大应力。一个目标函数可以用多个设计响 应来公式表示。如果设定目标函数最小化或者最大化设计响应，ABAQUS 拓扑优化模块则通 过增加每个设计响应值代入目标函数进行计算。另外，如果有多个目标函数，可以试用权重 因子定义每个目标函数的影响程度。 约束（Constraints）:  约束亦是从设计变量中萃取的一定范围的数值。然而，一个约束 不能由设计响应集合而来。约束限定了设计响应  ，比如可以指定体积必须降低 45%或者某 个区域的位移不能超过 1mm。约束也可以指定制造跟优化无关的制造或者几何约束，比如 轴承面的直径不能改变。 停止条件（Stop conditions）:  全局停止条件决定了优化的最大迭代次数。  局部停止条 件在局部最大/最小达成之后指定优化应该停止。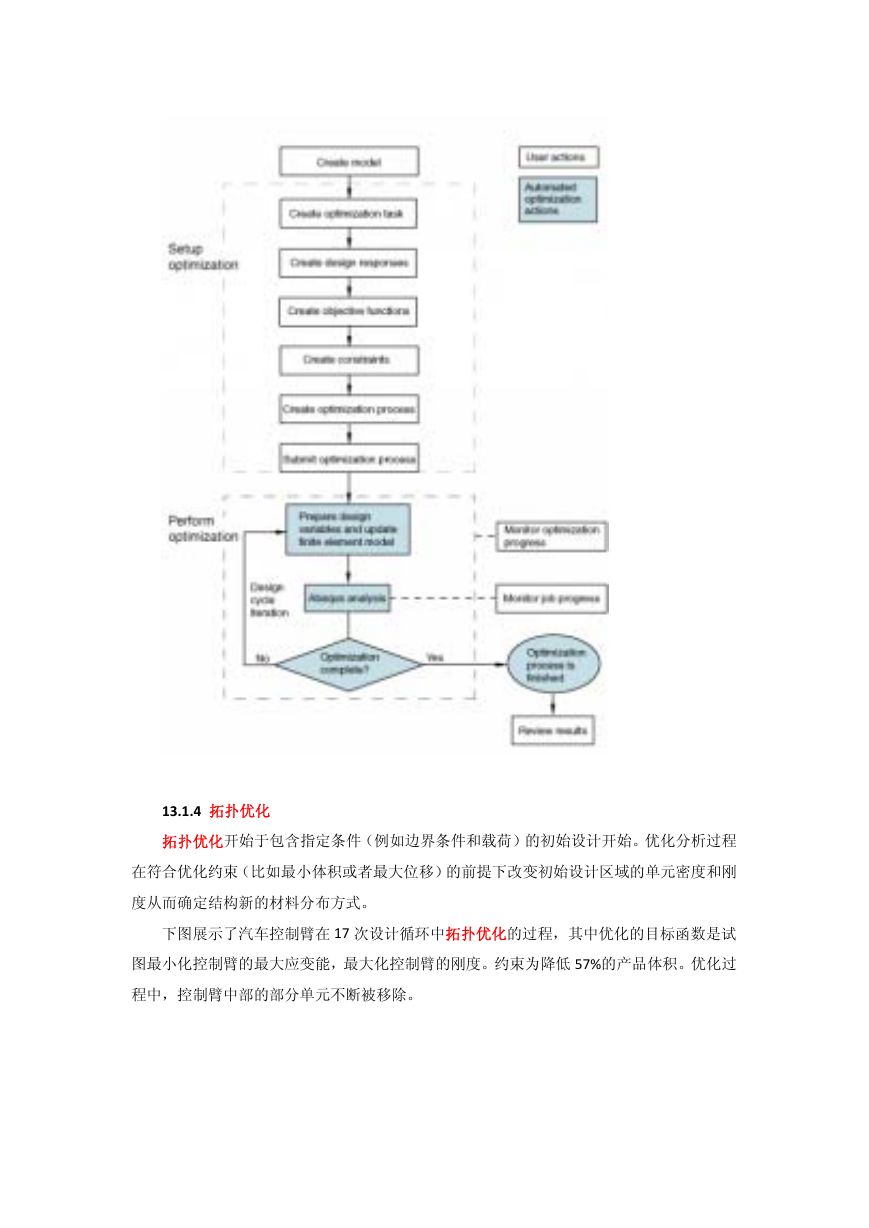 13.1.3 ABAQUS/CAE 结构优化步骤 下面的步骤需要合并到 ABAQUS/CAE 模型结构优化设计中： 1） 创建需要优化的 ABAQUS 模型。 2） 创建一个优化任务。 3） 创建设计响应。 4） 利用设计响应创建目标函数和约束。 5） 创建优化进程，提交分析。 基于优化任务的定义及优化程序，ABAQUS/CAE 拓扑优化模块进行迭代运算： 1） 准备设计变量（单元密度或者表面节点位置）。 2） 更新 ABAQUS 有限元模型。 3） 执行 ABAQUS/Standard 分析。 这些迭代或者设计循环不会停止，除非： 1） 最大迭代数达到 2） 指定的停止条件达到。 下图描述了 ABAQUS 优化分析的过程：
    13.1.4  拓扑优化 拓扑优化开始于包含指定条件（例如边界条件和载荷）的初始设计开始。优化分析过程 在符合优化约束（比如最小体积或者最大位移）的前提下改变初始设计区域的单元密度和刚 度从而确定结构新的材料分布方式。 下图展示了汽车控制臂在 17 次设计循环中拓扑优化的过程，其中优化的目标函数是试 图最小化控制臂的最大应变能，最大化控制臂的刚度。约束为降低 57%的产品体积。优化过 程中，控制臂中部的部分单元不断被移除。
    ABAQUS 可以应用如下目标到拓扑优化过程中： 1） 应变能（结构刚度的度量值） 2） 特征频率 3） 内力和支反力 4） 重量和体积 5） 重心 6） 惯性矩。 可以应用其他相同约束变量到拓扑优化分析中。另外，拓扑优化同样可以考虑标准产品 制造过程。例如铸造和冲压。可以冻结指定区域、应用数量尺寸、对称性及耦合约束。拓扑 优化的例子在 ABAQUS Example Problems Manual 的 Section11.1.1 中。 13.1.5  基于密度（一般）VS 刚度的拓扑优化 拓扑优化支持两种算法——一般算法比较灵活，可以应用到大多数问题中；基于刚度的 算法，更为有效，当时应用能力有限。ABAQUS 默认采用一般算法，但是当创建优化任务的 时候可以进行优化算法的选择。每种优化算法达到优化目标的过程是不同的。 算法 一般拓扑优化算法在满足目标函数和约束前提下使得密度及刚度较好地匹配设计变量， 可参考 Bends?e and Sigmund (2003)，文献中有一般算法的部分描述。相反的，刚度拓扑优 化作为一种更为有效的算法，使用了应变能和节点力作为输入量而且并不需要计算设计变量 的局部刚度。基于刚度的优化算法是德国卡尔斯鲁厄大学（U.Karlsruhe）的 Bakhtiary (1996) 提出的。 中间密度单元
    一般算法导致了最终设计中间单元的产生（相对密度处于 0~1 之间的单元）。相反地， 基于刚度的优化算法会产生不是空材料即是实体（0 或者 1）。 优化设计循环步 优化设计需要的循环步在优化计算开始的时候是并不知晓的，但是一般来说，这个步数 处于 30~45 之间。基于刚度的优化算法能够更快地达到优化算法的解（默认 15 步）。 分析类型 一般优化算法支持线性静力、非线性静力及线性模态分析。两种算法均支持几何非线性 和接触，以及很多非线性材料。 此外，静力拓扑优化中可以指定位移。然而，模态分析不可指定位移。拓扑优化支持符 合材料分析，个别复合材料的碾压分析是不支持的，如不能指定复合材料纤维走向等。 目标函数和约束 一般优化算法可以使用一个目标函数和数个约束，这些约束可以全部是不等式。多种设 计响应可以被定义为目标和约束，例如应变能、位移和旋转、支反力及内力、特征频率和材 料的体积及重量。基于刚度的拓扑优化算法更为有效，然而适用性比较差，仅支持应变能（一 种刚度的两度）作为目标函数，材料体积作为约束方程。 13.1.6  形状优化 形状优化采用了跟基于刚度的拓扑优化算法类似的算法。形状优化一般是对表面节点进 行较小的调整以减小局部应力集中。形状优化用于产品外形需要微调的情况。 形状优化试图重置既定区域的表面节点位置直到此区域的应力成为常数（应力均匀）。 下图是连杆形状优化以减小局部应力集中的例子： 形状优化支持一下目标： 1） 应力和接触应力
    2） 自然频率 3） 弹性、塑性、全应变和应变能密度 形状优化只能应用体积约束，另外，可以使用一定数量的制造几何限制条件使提出的设 计能够继续铸造或者冲压过程。也可以冻结某特定区域、应用数量尺寸、对称性及耦合限制 等。 形状优化的网格光顺 形状优化过程中，ABAQUS/CAE 拓扑优化模块修改模型表面。如果拓扑优化模块，只对 表面节点进行位置调整而不对表层内节点进行调整，单元将会发生扭曲现象。这样，ABAQUS 的优化结果将变得不可信。 为了获得相当质量的表面单元，ABAQUS/CAE 拓扑优化模块可以对既定区域进行网格光 顺，从而使得内外节点位置关系更加和谐。需要注意的是，在进行优化之前，指定区域必须 具有较好的网格质量。 ABAQUS/CAE 拓扑优化模块可以光顺标准连续单元，比如三角形单元、四边形单元和四 面体单元。其他单元类型将不会被光顺化。可以指定光顺单元的倾斜角度或者单元质量。 网格光顺化是一个比较耗费计算量的过程。光顺算法是基于单元的，计算时间也会随着 区域内单元密度及自由度情况响应增加。因此，可以只对优化区域内的单元指定网格光顺化。 网格光顺化的区域节点必须是自由的，不能应用于有约束的节点或者区域。网格光顺化的设 定具体参见 ABAQUS/CAE 用户手册。 网格光顺化可以应用到优化区域也可以应用到非优化区域，然而优化区域必须包含于网 格光顺化指定区域。 ABAQUS/CAE 在网格光顺化中会自动将所有表面单元进行约束，从而使优化结果得到保 存。然而可以选择设计区域附近的表层节点进行光顺化移动，从而使得优化区域和非优化设 计区域能够更加连续。 默认的网格光顺化采用强制拉普拉斯网格光顺化算法。但是，如果模型比较小，比如小 于 1000 个节点，可以采用局部梯度化网格光顺算法。在每次运算中，局部梯度化网格光顺 算法进行质量不好的单元的辨别，然后通过移动节点对其进行光顺。局部梯度化光顺通常产 生具有最佳外形的单元。对于较大模型，局部梯度化网格光顺算法一般会在最佳网格质量形 成之前停止，这样只有最坏的单元质量得到了光顺。 ABAQUS拓扑优化手册-OverView.doc (103 KB, 下载次数: 81) -----------------------分割线-------------------------20120601 更新 by songerking 13.2  优化模型
    13.2.1 设计响应 13.2.1.1 概述 一个设计响应： 1) 是一个单范围值，例如结构的体积 2) 通过 ABAQUS/CAE 读取 odb 文件的结果和模型文件来计算 3) 与目标函数和约束相关联（比如，可以创建一个目标函数和约束去最小化节点位移 或者强制降低结构重量 50%以上） 4) 必须在一定的分析过程基础上（比如，在对既定区域选择最大化最小特征频率则需 要进行提取特征频率的分析） 尽管已有一些限制应用到了响应上，还必须在 ABAQUS/CAE 拓扑优化模块中通过操作来 或者设计响应的范围值。例如，一个体积设计响应可以只用于设计区域的体积之和，计算 von Mises 应力的设计响应必须是模型中一定区域的应力最大值。如下设计响应操作为 ABAQUS/CAE 拓扑优化模块（以后简称 ATOM）所提供： 最小化或者最大化：既定区域的最小值或者最大值。ATOM 允许的最大值操作为：应力， 接触应力和应变设计响应。 求和：既定区域所有值求和值。ATOM 允许体积、重量、惯性矩和重力设计响应的和值 优化。 13.2.1.2 基于刚度的拓扑优化设计响应 ATOm 提供基于刚度的拓扑优化方法以应变能和体积设计响应。 应变能 结构的顺从性是结构挠性及刚性的量度，被定义为所有单元的应变能之和。顺从性与刚 度成反比，因此最小化顺从性计算最大化全局刚度。如果载荷是集中力或者面力，则必须 选择最小化应变能而不是最大化整体刚度；而如果载荷是热应力场，优化就会在使得结构 变软的同时，应变能不断减小，因为降低应变能会导致硬化，所以应该一直选择最大化应 变能。另外，如果模型指定了位移，则须最大化应变能。 拓扑优化考虑所有单元的总应变能，因此，如果选择应变能作为目标函数，则须将目标 应用于整个模型。优化过程中不能使用应变能作为约束。 Abaqus/CAE  Optimization module: Task stiffness topology task, Design Usage:  Response Create: Single-term, Variable Strain energy 体积 体积是设计区域内所有单元体积之和。对于大多数优化问题，需要给定一个 ABAQUS 模型。但是如果最小化应变能（最大化刚度）。如果优化需要最小化应变能，则不可用体 积作为约束。
    Abaqus/CAE  Optimization module: Task stiffness topology task, Design Usage:  Response Create: Single-term, Variable: Volume 13.2.1.3 基于密度的拓扑优化（一般拓扑优化）设计响应 ATOM 一般拓扑优化算法支持重心、平动、旋转、特征频率、惯性矩、内力、反力、力 矩、应变能、体积和重量设计响应。 重心 在优化分析中将指定区域的重心作为一个设计变量，并且可以选择三个主分量： 当ATOM计算重心时，单元会以当前相对密度为计算依据。  举例说明，当需要约束 Y 方向的重心在某个范围内的时候，这即为一个重心优化问题。 设计响应会考虑整个模型或者指定区域的重心位置。 如果使用了局部坐标系，ATOM 会根据坐标轴和原点重新计算重心。如果不选择使用局 部坐标系，ATOM 将使用整体坐标系。 壳体及膜区域的重心在 ATOM 中考虑其厚度后作为三维区域处理的。ATOM 只能对拓扑 优化支持的单元类型计算重心。因此，ATOM 计算得到的重心跟 ABAQUS/Stardard 和 ABAQUS/Explicit 不同，例如，ATOM 不会考虑线区域。
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料