一种改进的永磁同步电机模型预测控制.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：1.98M 资料格式：pdf 举报版权申诉

weixin_38708105-14138392-16359647472982884993.pdf-第1页.png

第1页 / 共7页

weixin_38708105-14138392-16359647472982884993.pdf-第2页.png

第2页 / 共7页

weixin_38708105-14138392-16359647472982884993.pdf-第3页.png

第3页 / 共7页

weixin_38708105-14138392-16359647472982884993.pdf-第4页.png

第4页 / 共7页

weixin_38708105-14138392-16359647472982884993.pdf-第5页.png

第5页 / 共7页

weixin_38708105-14138392-16359647472982884993.pdf-第6页.png

第6页 / 共7页

weixin_38708105-14138392-16359647472982884993.pdf-第7页.png

第7页 / 共7页

文本预览

第 37 卷第４期２０17 年４月电力自动化设备ＥｌｅｃｔｒｉｃＰｏｗｅｒＡｕｔｏｍａｔｉｏｎＥｑｕｉｐｍｅｎｔＶｏｌ．37 Ｎｏ．４Ａpr. 2017 一种改进的永磁同步电机模型预测控制高逍男，陈希有（大连理工大学电气工程学院，辽宁大连 116024）摘要：利用传统的模型预测控制算法确定下一时刻所要应用的开关状态时，需遍历变换器的全部开关状态，计算量较大，不利于在线应用。对此，提出了一种改进的永磁同步电机模型预测控制算法，通过求出期望的电压矢量角，确定电压矢量所在扇区，进而减少算法对开关状态的选择数量，使算法的计算量得到显著降低。实验结果说明，采用所提改进模型预测控制算法，系统具有较好的电流动态特性和较小的纹波电流。关键词：永磁同步电机；电流控制；模型预测控制；数学模型中图分类号： TM 921 文献标识码： A DOI： 10.16081 ／ j.issn.1006 - 6047.2017.04.030 0 引言目前，在众多永磁同步电机（PMSM）控制方法中，存在２种高性能调速控制方法：磁场定向控制（FOC）和直接转矩控制（DTC）［1］。 FOC 方法通过分别控制定子电流的交、直轴分量实现电机转矩和磁链的解耦控制，其特点是稳态精度高，中、低速下具有很好的控制性能。但在数字化实现过程中，控制器的输出滞后于系统电流的变化，从而影响电流的静、动态响应。 DTC 方法通过采用非线性滞环控制器，基于一种查表逻辑选择出合适的开关状态，从而实现对电机转矩和磁链的独立控制。其特点是控制方法简单、动态响应快、鲁棒性强。模型预测控制（MPC）方法作为近些年兴起的控制策略，同 FOC 相比，无需电流内环及参数整定（其本质是用ＭＰＣ替代传统的电流内环控制），直接产生逆变器驱动信号而无需脉宽调制，易于处理系统约束或增加其他控制目标，具有结构简单、动态响应快和易于扩展等优点［2］。 MPC 与 DTC 有许多相似之处，均具有动态响应快、控制方法简单且在一个开关周期内只选择一种开关状态作为输出等特点。但二者在控制思想上存在不同，这也导致 2 种方法在电机控制效果上存在到最小值的开关状态，需要对电力变换器中所有可能的开关状态进行评价。所以，在一般情况下，MPC 方法与 DTC、FOC 方法相比，计算量更大，计算时间更长。虽然对于三相两电平逆变器而言，用常规的电流预测控制方法计算 7 种开关状态的预测值并不难，但在一些特殊应用场合，如多电平变换器控制、多约束条件和多目标控制、鲁棒控制、无速度传感器控制等，其增加的计算时间可能会导致开关周期超过允许的采样时间。即使不超过允许采样时间，与经典的 DTC 和 FOC 相比，过长的开关周期也会使 MPC 的控制效果下降。文献［4］给出了一种简化的 MPC 算法，使原本需要评价 7 种开关状态的预测值降低为只要评价 3 种开关状态，但文中只介绍了在静止负载条件下如何计算期望电压矢量角，从而减少开光状态的选择，并未给出诸如电机等旋转负载的期望电压矢量角的计算方法。本文提出了一种改进的永磁同步电机 MPC 方法。通过对电机电压矢量图的分析，提出了一种永磁同步电机作为负载情况下的期望电压矢量角的计算方法（此方法可扩展到一般的交流电机）。与传统的 MPC 方法相比，本文提出的方法可以显著减少算法的计算时间，从而缩短开关周期，而控制间隔的减小可使系统具有较好的动态响应特性和较小的纹波着优劣之分。简单地说，DTC 方法选择开关状态的电流。原则是为了消除期望转矩与实际转矩之间的误差。 MPC 方法则是在计算周期内选择使期望值与预测值误差最小的开关状态，并且该方法是在实际误差产生之前应用预先确定的开关状态，这使得 MPC 方法在开关状态选择上更加准确有效。根据文献［3］，在相同硬件条件下，MPC 方法要优于 DTC 方法。然而，传统的 MPC 方法为选出能使质量函数达收稿日期：２016 －０３－ 2８；修回日期：２０１7 － 02 - 13 基金项目：国家自然科学基金资助项目（50877007） Project supported by the National Natural Science Foundation of China（50877007） 1 系统数学模型ＭＰＣ方法结构框图见图 1［５鄄８］。开关状态 MPC i* d，i* q ω id，iq abc ia，ib，ic dq d ／ d t PMSM θ 图 1 MPC 算法框图 Fig.1 Block diagram of MPC algorithm

电力自动化设备第 37 卷根据电机学原理，永磁同步电机在同步旋转坐标系下的电压方程为： e ud= Rid+ uq= Riq+ dψd dt dψq dt - ψqωe - ψd ωe （1）其中，ψd = Ldid + ψf 为直轴磁链；ψq = Lq iq 为交轴磁链； ud、uq 分别为定子直、交轴电压；id、iq 分别为直、交轴定子电流；ωe 为电角频率； ψf、R、Ld、Lq 分别为永磁体磁链、定子电阻、直轴电感和交轴电感。本文用到的电机为表贴式永磁同步电机，所以有 Ld = Lq = L。选择电机电流为状态变量，由式（1）可以得到式（2）所示的状态方程： t did dt diq dt = t - R L ωe - ωe - R L q+ id iq 1 L 0 t 0 1 L q - ud uq t 0 ωeψf L （2）其中，R、L 和 ψf 为常量，在采样周期 T 较小的情况下，电角度的变化在一个采样周期 T 内可以忽略。将式（2）的状态方程离散化并做近似处理得到： id（k） iq（k）q ＋Ｇ ud（k） uq（k）q + H（k）（3） = F（k） 1- TR L q id（k + 1） iq（k + 1） F（k） = t T ωe（k） - Tωe（k） 1- TR L G = T L 0 t 0 T L ， H（k） = t 0 - Tψf L ωe（k）其中，ud（k）、uq（k）可由逆变器的输出电压经过 dq 变换得到。根据式（3）就能从第 k 个周期得到第 k + 1 个周期电流的预测值。 2 传统的 MPC 算法 MPC 算法是利用质量函数来确定系统在下一个采样周期所要应用的开关状态［８鄄１５］。本文所使用的质量函数为： d - id（k + 1） + i* g = i* （4） q 为系统期望输出的电流值。由于使用的是 q - iq（k + 1） d 取 0，i* q 可由速度环反馈得到。 d 、i* 其中，i* id= 0 控制方案，故 i* 由质量函数式（4）可知，需要找到一组 id（k + 1）和 iq（k + 1），使得式（4）中的 g 值最小。由式（3）可知，在 kT 到（k + 1）T 内，id（k + 1）、iq（k + 1）的值取决于 ud（k）、uq（k）。不同的 ud（k）、uq（k）则会产生不同的 id（k + 1）、iq（k + 1）。逆变器可输出 7 种不同的电压矢量，这会产生 7 组不同的 id（k + 1）、iq（k + 1）。传统的ＭＰＣ算法就是将这 7 组电流预测值代入质量函数中，求得使 g 值最小的一组 id（k + 1）、iq（k + 1），进而找出系统在下一时刻所需要的开关状态。具体过程如图 2 所示。测量 θe（k）、ωe（k）、i（k）、Udc（k）计算 F（k）、H（k） l = 1 由式（3）计算 il（k + 1）计算 gl l = l + 1 l ＞ 7？ Y N 选出最小值 gmin 并应用其所对应的开关状态图 2 传统的 MPC 算法流程 Fig.2 Flowchart of traditional MPC algorithm 3 改进的 MPC 算法传统的 MPC 算法是在每一个采样周期内，从全部的 7 种电压矢量中找出使质量函数取得最小值的电压矢量。这种方法类似于穷举法。如果知道期望的电压矢量在 α β 坐标系下的电角度，就可以缩小电压矢量的选择范围［4］。在 MPC 中，存在一种期望的电压矢量，通过在逆变器上施加这种旋转的电压矢量可以带动电机磁链矢量以角速度 ωe 旋转。而这种电压矢量可以看作是有效的电压矢量和零矢量的组合。而应用传统的 MPC 算法得到的有效电压矢量总是频繁地落在期望电压矢量所在扇区。这意味着在应用 MPC 算法的时候不需要遍历所有的有效电压矢量，如果知道期望的电压矢量所在扇区，则只需要在该扇区边界的 2 个有效电压矢量与零矢量 3 个电压矢量之间进行选择即可。这种改进的 MPC 算法显著减少了计算时间，从而缩短开关周期。虽然所提方案并未考虑系统的暂态过渡过程，但从实验部分来看，其跟踪延时在两电平逆变器中并未体现，而较短的采样周期也可使系统更快追踪到暂态过程所需要的电压矢量。改进算法的电压矢量选择方式如图 3 所示。从图 3 可以看出，只要知道 θvref，就可以确定期望的电压矢量所在扇区，从而找出 3 个电压矢量进行选择。从算法的角度看，这种改进的 MPC 算法就是在原有算法的基础上引入启发式，即期望电压矢量的电角度 θvref。所以，这种算法的关键在于如何计算期望电压矢量角 θvref。图 4 为忽略定子电阻压降条件下的永磁同步电

第 4 期高逍男，等：一种改进的永磁同步电机模型预测控制测量 θe（k）、ωe（k）、i（k）、Udc（k）计算 F（k）、H（k）、θvref 并判断其所在扇区得到该扇区对应的 3 个电压矢量 U0、U1、U2 l = 0 代入 Ul，计算 il（k + 1）计算 gl l = l + 1 l ＞ 2？ Y N 选出最小值 gmin 并应用其所对应的开关状态 U2（010） β 2 需遍历的电压矢量 U6（110） u* s U3（011） 3 4 1 U4（１０0） α θvref U０，U7 6 5 U1（001） U5（１０１）图 3 改进的 MPC 算法电压矢量的选择方式 Fig.3 Voltage vector selection of improved MPC algorithm is us q iq δ φ  ψs 图 5 改进的 MPC 算法流程 Fig.5 Flowchart of improved MPC algorithm δ id O θe ψd ψf ωe d α 图 4 永磁同步电机的空间矢量图 Fig.4 Space vector diagram of PMSM 机空间矢量图，其中 φ 为功率因数角， 为内功率因数角，δ 为功角（或转矩角），θe 为定子电角度，ωe 为电角频率。当忽略定子电阻时，定子磁链 ψs 与定子上的电压矢量 us 相角差为 π／２。由图 4 可以得出，电压矢量的角度可表示为： θv= θe+ δ + π／２（5）其中，δ=arctan（ψq ／ ψd）；θe 在一个采样周期 T 内，可近似看成常量。本文应用的是 i* d = 0 的控制方案，再根 q 可以得到 ψ* 据速度环反馈的 i* d = ψf 和 ψ* q，从而求出 δ* = arctan（ψ* q ／ ψ* d ），修改式（5）就可得到期望的电压矢量角： q = Lqi* （6）图 5 给出了一个开关周期内改进 MPC 算法的 θvref = θe+ δ*+π／２流程图。需要说明的是，由于存在着采样时间、计算时间以及在较复杂的电力变换器中存在的换流时间等一系列延时，在实际系统中，无法在当前时刻 kT 立刻得出 kT 到（k+1）T 时间段内所要应用的开关状态。所以，实际的 MPC 算法预测的是下一时间段，即（k + 1）T 到（k + 2）T 使用的开关状态。而在当前时刻 kT 则应用上一时间段［（k - 1）T，kT］所得出的开关状态。图 6 描述了实际系统中 MPC 算法的工作过程。从图中可以看到，由于采样周期 T 很短，假设在 kT 到（k + 2）T 这段时间，系统的期望参考值 i* 不变， S（k ） i（k + 1） i* ij（k + 2） ij+1（k + 2） ij+2（k + 2） ij+3（k + 2） … … kT （k + 1）T （k + 2）T 图 6 实际系统中 MPC 算法的工作过程 Fig.6 Procedures of MPC algorithm in practical system 在 kT 时刻应用开关状态 S（k），根据负载模型得到（k + 1）T 时刻电流的理论计算值 i（k + 1），遍历可选的开关状态得到（k+2）T 时刻电流的预测值 ij（k+2），找出与参考值 i* 最接近的那个预测值 iop（k+2），如图中最接近的值应为 ij+2（k + 2），则该预测值所对应的开关状态 Sop（k+1）即为下一时刻系统采用的开关状态。 4 实验结果依据图 1 搭建了实验平台，逆变器的可控功率管为三菱 PM75CLA120 的 IPM 模块；负载为永磁同步电机，型号为 110SJT－M040D，额定功率为 1 kW，额定转速为 2 500 r ／ min，相电阻为Ｒ＝ 1.09 Ω，电感Ｌd = Ｌq= 3.3 mH，编码器线数为 2 500 线／圈，磁极对数为 4；控制单元的核心是 DSP，型号 TMS320F28335。改进 MPC 算法的程序运行时间是 45μs（采样周期选为 50 μs），而传统 MPC 算法的执行时间是 64 μs（采样周期选为 70 μs）。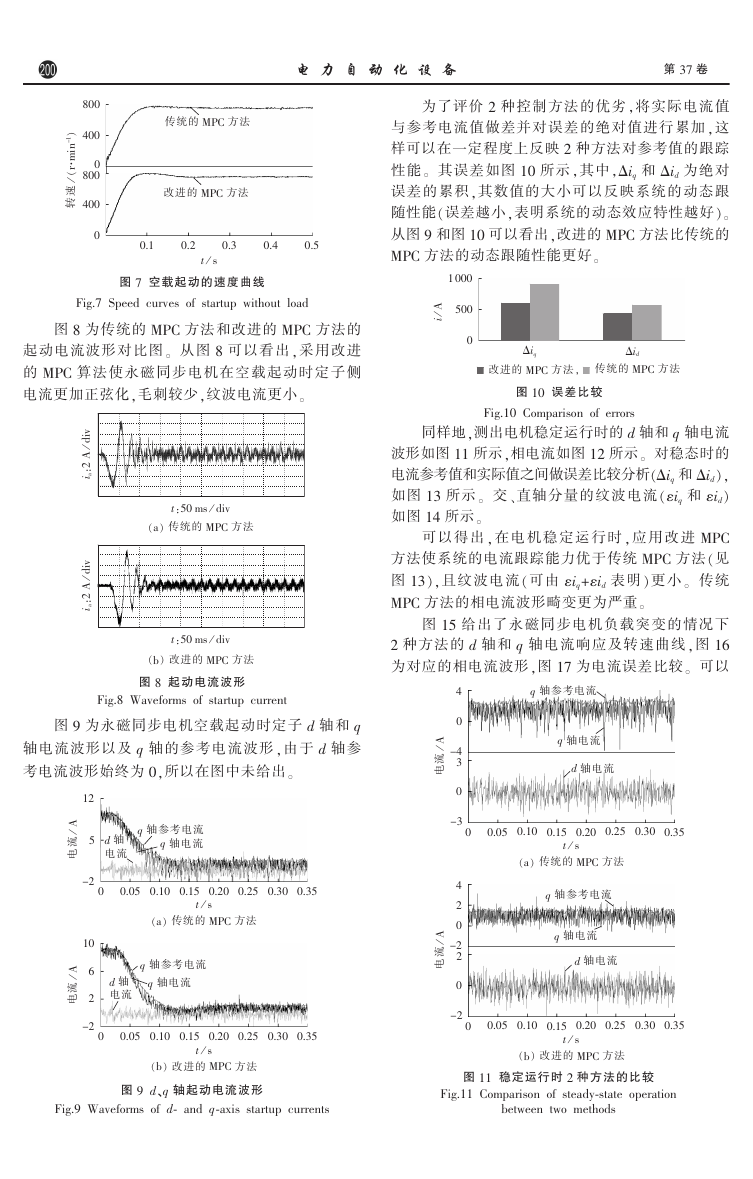图 7 为空载阶跃起动时，传统 MPC 方法和改进 MPC 方法的速度响应曲线，速度给定为 750 r ／ min。对比 2 条速度曲线可以看出，改进 MPC 方法的速度波动更小，2 种方法的响应时间相近。

电力自动化设备第 3７卷） 1 - n i m r· （／速转 800 400 0 800 400 0 传统的 MPC 方法改进的 MPC 方法 0.1 0.2 0.3 0.4 0.5 t ／ s 为了评价 2 种控制方法的优劣，将实际电流值与参考电流值做差并对误差的绝对值进行累加，这样可以在一定程度上反映 2 种方法对参考值的跟踪性能。其误差如图 10 所示，其中，Δiq 和 Δid 为绝对误差的累积，其数值的大小可以反映系统的动态跟随性能（误差越小，表明系统的动态效应特性越好）。从图 9 和图 10 可以看出，改进的 MPC 方法比传统的 MPC 方法的动态跟随性能更好。图 7 空载起动的速度曲线 Fig.7 Speed curves of startup without load 图 8 为传统的 MPC 方法和改进的 MPC 方法的起动电流波形对比图。从图 8 可以看出，采用改进的 MPC 算法使永磁同步电机在空载起动时定子侧电流更加正弦化，毛刺较少，纹波电流更小。 1 000 Ａ／ i 500 0 Δiq Δid 改进的 MPC 方法，传统的 MPC 方法图 10 误差比较 Fig.10 Comparison of errors v i d ／ A 2 ： a i v i d ／ A 2 ： a i t：50 ms ／ div （a）传统的 MPC 方法 t：50 ms ／ div （b）改进的 MPC 方法图 8 起动电流波形 Fig.8 Waveforms of startup current 图 9 为永磁同步电机空载起动时定子 d 轴和 q 轴电流波形以及 q 轴的参考电流波形，由于 d 轴参考电流波形始终为 0，所以在图中未给出。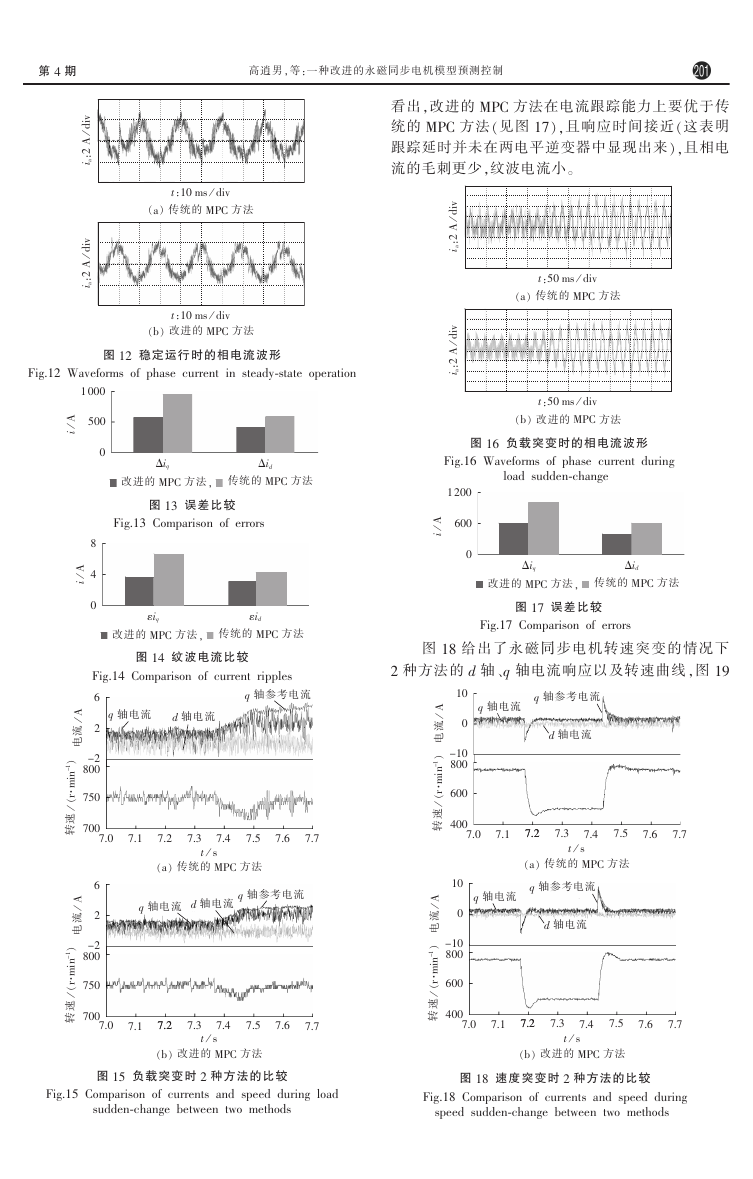 12 Ａ／流电 5 d 轴电流 q 轴参考电流 q 轴电流 -2 10 Ａ／流电 6 2 -2 0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 t ／ s （a）传统的 MPC 方法 q 轴参考电流 q 轴电流 d 轴电流 0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 t ／ s （b）改进的 MPC 方法图 9 d、q 轴起动电流波形 Fig.9 Waveforms of d鄄 and q鄄axis startup currents 同样地，测出电机稳定运行时的 d 轴和 q 轴电流波形如图 11 所示，相电流如图 12 所示。对稳态时的电流参考值和实际值之间做误差比较分析（Δiq 和 Δid），如图 13 所示。交、直轴分量的纹波电流（εiq 和 εid）如图 14 所示。可以得出，在电机稳定运行时，应用改进 MPC 方法使系统的电流跟踪能力优于传统 MPC 方法（见图 13），且纹波电流（可由 εiq+εid 表明）更小。传统 MPC 方法的相电流波形畸变更为严重。图 15 给出了永磁同步电机负载突变的情况下 2 种方法的 d 轴和 q 轴电流响应及转速曲线，图 16 为对应的相电流波形，图 17 为电流误差比较。可以Ａ／流电Ａ／流电 4 0 -4 3 0 -3 4 2 0 -2 2 0 -2 q 轴参考电流 q 轴电流 d 轴电流 0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 t ／ s （a）传统的 MPC 方法 q 轴参考电流 q 轴电流 d 轴电流 0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 t ／ s （b）改进的 MPC 方法图 11 稳定运行时 2 种方法的比较 Fig.11 Comparison of steady鄄state operation between two methods

第 4 期高逍男，等：一种改进的永磁同步电机模型预测控制 v i d ／ A 2 ： a i v i d ／ A 2 ： a i t：10 ms ／ div （a）传统的 MPC 方法 t：10 ms ／ div （b）改进的 MPC 方法图 12 稳定运行时的相电流波形 Fig.12 Waveforms of phase current in steady鄄state operation 1 000 Ａ／ i 500 0 Ａ／ i 8 4 0 Δiq Δid 改进的 MPC 方法，传统的 MPC 方法图 13 误差比较 Fig.13 Comparison of errors εiq εid 改进的 MPC 方法，传统的 MPC 方法图 14 纹波电流比较 Fig.14 Comparison of current ripples q 轴电流 d 轴电流 q 轴参考电流 6 2 Ａ／流电） 1 - n i m r· （／速转 -2 800 750 700 7.0 6 2 Ａ／流电） 1 - n i m r· （／速转 -2 800 750 700 7.0 7.1 7.2 7.3 7.4 7.5 7.6 7.7 t ／ s （a）传统的 MPC 方法 q 轴电流 d 轴电流 q 轴参考电流 7.1 7.2 7.2 7.3 7.4 7.5 7.6 7.7 t ／ s （b）改进的 MPC 方法看出，改进的 MPC 方法在电流跟踪能力上要优于传统的 MPC 方法（见图 17），且响应时间接近（这表明跟踪延时并未在两电平逆变器中显现出来），且相电流的毛刺更少，纹波电流小。 v i d ／ A 2 ： a i v i d ／ A 2 ： a i t：50 ms ／ div （a）传统的 MPC 方法 t：50 ms ／ div （b）改进的 MPC 方法图 16 负载突变时的相电流波形 Fig.16 Waveforms of phase current during load sudden鄄change 1 200 Ａ／ i 600 0 Δiq Δid 改进的 MPC 方法，传统的 MPC 方法图 17 误差比较 Fig.17 Comparison of errors 图 18 给出了永磁同步电机转速突变的情况下 2 种方法的 d 轴、q 轴电流响应以及转速曲线，图 19 Ａ／流电） 1 - n i m r· （／速转 q 轴参考电流 q 轴电流 d 轴电流 10 0 -10 800 600 400 7.0 7.1 7.2 7.2 7.3 7.4 7.5 7.6 7.7 t ／ s （a）传统的 MPC 方法Ａ／流电） 1 - n i m r· （／速转 q 轴参考电流 q 轴电流 d 轴电流 10 0 -10 800 600 400 7.0 7.1 7.2 7.2 7.3 7.4 7.5 7.6 7.7 t ／ s （b）改进的 MPC 方法图 15 负载突变时 2 种方法的比较 Fig.15 Comparison of currents and speed during load sudden鄄change between two methods 图 18 速度突变时 2 种方法的比较 Fig.18 Comparison of currents and speed during speed sudden鄄change between two methods

电力自动化设备第 37 卷 of predictive current control schemes for a permanent鄄magnet synchronous machine drive［J］. IEEE Transactions on Industrial Electronics，2009，56（7）：2715鄄2728. ［4］ ZHANG Y，LIN H. Simplified model predictive current control method of voltage鄄source inverter［C］∥2011 IEEE 8th International Conference on Power Electronics and ECCE Asia （ICPE & ECCE）. ［S.l.］：IEEE，2011：1726鄄1733. ［5］ LIN鄄SHI X，MOREL F，LLOR A M，et al. Implementation of hybrid control for motor drives［J］. IEEE Transactions on Industrial Electronics，2007，54（4）：1946鄄1952. ［6］ MOON H T，KIM H S，YOUN M J. A discrete鄄time predictive current control for PMSM［J］. IEEE Transactions on Power Electronics，2003，18（1）：464鄄472. ［7］牛里，杨明，刘可述，等. 永磁同步电机电流预测控制算法［J］. 中国电机工程学报，2012，32（6）：131鄄137. NIU Li，YANG Ming，LIU Keshu，et al. A predictive current control scheme for permanent magnet synchronous motors［J］. Proceedings of the CSEE，2012，32（6）：131鄄137. ［8］吴振兴，邹云屏，张哲宇，等. 单相 PWM 整流器的输入电流自适应预测控制器［J］. 电工技术学报，2010，25（2）：73鄄79. WU Zhenxing，ZOU Yunping，ZHANG Zheyu，et al. Adaptive predictive controller of supply current applied in single鄄phase PWM rectifier［J］. Transactions of China Electrotechnical Society， 2010，25（2）：73鄄79. ［9］王宏佳，徐殿国，杨明. 永磁同步电机改进无差拍电流预测控制［J］. 电工技术学报，2011，26（6）：39鄄45. 为对应的相电流波形。图 20 为通过对实际电流和参考电流的误差进行比较来反映系统的动态跟随性能。 v i d ／ A 2 ： a i v i d ／ A 2 ： a i t：100 ms ／ div （a）传统的 MPC 方法 t：100 ms ／ div （b）改进的 MPC 方法图 19 速度突变时的相电流波形 Fig.19 Waveforms of phase current during speed sudden鄄change 900 Ａ／ i 450 0 Δiq Δid WANG Hongjia，XU Dianguo，YANG Ming. Improved deadbeat 改进的 MPC 方法，传统的 MPC 方法 predictive current control strategy of permanent magnet motor 图 20 误差比较 Fig.20 Comparison of errors 同样地，当电机速度发生变化时，应用改进的 MPC 方法使系统的电流跟踪性能优于传统的 MPC 方法（见图 20），且速度达到稳定时的波动较小。而 2 种方法的暂态过程响应时间接近。 5 结论本文提出的改进永磁同步电机 MPC 方法，通过求出期望的电压矢量角，确定电压矢量所在扇区，进而减少 MPC 算法中对开关状态的判定数量，即从传统的 7 种到改进之后的 3 种状态，大幅降低了算法的计算时间，缩短了开关周期。通过实验验证了本文所提出的改进 MPC 方法在对电流的动态跟随性能以及稳态性能方面的表现均优于传统的 MPC 方法，同时也减少了电流纹波。参考文献： drives［J］. Transactions of China Electrotechnical Society，2011，26 （6）：39鄄45. ［10］沈坤，章兢，王玲,等. 三相电压型逆变器模型预测控制［J］. 电工技术学报，2013，28（12）：283鄄289. SHEN Kun，ZHANG Jing，WANG Ling，et al. Model predictive control of three鄄phase voltage source inverter ［J］. Transactions of China Electrotechnical Society，2013，28（12）：283鄄289. ［11］吴德会，李钷. 基于 FCS鄄MPC 的电压跟踪调制方法［J］. 电力自动化设备，2015，35（3）：101鄄107. WU Dehui，LI Ju. Voltage tracking modulation method using FCS鄄MPC［J］. Electric Power Automation Equipment，2015，35 （3）：101鄄107. ［12］杨兴武，冀红超，甘伟. 基于模型预测控制的并网逆变器开关损耗优化方法［J］. 电力自动化设备，2015，35（8）：84鄄89. YANG Xingwu，JI Hongchao，GAN Wei. Switching loss optimization based on model predictive control for grid鄄 connected inverter［J］. Electric Power Automation Equipment， 2015，35（8）：84鄄89. ［13］ ZHANG Z，XU H，XUE M，et al. Predictive control with novel virtual鄄flux estimation for back鄄to鄄back power converters ［J］. IEEE Transactions on Industrial Electronics，2015，62（5）：2823鄄 2834. ［1］ KAZMIERKOWSKI M P，FRANQUELO L G，RODRIGUEZ J，et ［14］ ZHANG Z，FENG X，FANG H，et al. Ripple鄄reduced MPDPC al. High鄄performance motor drives［J］. IEEE Industrial Electronics Magazine，2011，5（5）：6鄄26. for active front end power converters with extended switching vectors and time鄄optimized control［J］. IET Power Electronics，［2］ RODRIGUEZ J，KENNEL R M，ESPINOZA J R，et al. High鄄 2016，9（9）. performance control strategies for electrical drives：an experi鄄 mental assessment［J］. IEEE Transactions on Industrial Electronics，［15］肖健梅，张科，王锡淮. 基于预测函数与线性多变量反馈控制的同步发电机励磁控制［J］. 电力自动化设备，2015，35（7）：153鄄 2012，59（2）：812鄄820. 159. ［3］ MOREL F，LIN鄄SHI X，RETIF J M，et al. A comparative study （下转第 217 页 continued on page 217）

第 4 期邹延生，等：基于协同控制理论的非线性直流附加控制器设计 Design of nonlinear ＨＶＤＣ supplementary controller based on synergetic control ZOU Yansheng，DONG Ping （School of Electric Power，South China University of Technology，Guangzhou 510640，China） Abstract： Aiming at the nonlinearity of large AC ／ DC power system and the inaccuracy of its model，a DC supplementary controller based on SGC（SynerGetic Control） is designed and applied to the multi鄄area AC ／ DC power system to enhance its transient stability. Appropriate macro鄄variable and manifold are designed according to the inertia center of each area，the analytic expression of SGC鄄based DC supplementary controller is deduced，and with the minimum angle frequency offset and the minimum DC power offset of inertia center as the objectives，the controller parameters are optimized by genetic algorithm. The areal designed controller is applied to a two鄄area AC ／ DC power system and a multi鄄infeed AC ／ DC power system respectively，and the time鄄domain simulations based on their PSCAD models demonstrate that，the proposed SGC method has better control effect in the inter鄄area oscillation damping than the conventional pole placement method and sliding mode control method. Furthermore，with strong robustness，the designed controller is immune to load model，operation mode and wide鄄area measuring signal delay，and its deduction has little dependence on the system model. Key words： HVDC power transient stability； robustness ssssssssssssssssssssssssssssssssssssssssssssss （上接第 202 页 continued from page 202） transmission； supplementary controller； synergetic control； inertia center； XIAO Jianmei，ZHANG Ke，WANG Xihuai. Excitation control 向为矩阵变换器、电力电子技术（E鄄mail： based on predictive function control and linear multi鄄variable kaixin5229@163.com）； feedback control for synchronous generator ［J］. Electric Power Automation Equipment，2015，35（7）：153鄄159. 陈希有（1962—），男，黑龙江哈尔滨人，教授，博士研究生导师，研究方向为无线电能传输、绿色电能变换。作者简介：高逍男（1990 —），男，山东蓬莱人，硕士研究生，研究方高逍男 Improved model predictive control of permanent magnet synchronous motor （College of Electrical Engineering，Dalian University of Technology，Dalian 116024，China） GAO Xiaonan，CHEN Xiyou Abstract： All switching statuses of converter should be traversed over when traditional MPC （Model Predictive Control） algorithm is applied to determine the switching status of next cycle，which is unfavorable to the real鄄time implementation due to its higher computational load. An improved MPC algorithm of PMSM （Permanent Magnet Synchronous Motor） is proposed，which determines the sector of voltage vector based on the expected voltage vector angle to reduce the selected switching statuses for cutting down the computational load. Experimental results show that，the system with the proposed MPC algorithm has better current response and smaller current ripple. Key words： permanent magnet synchronous motor； electric current control； model predictive control； mathematical models

分享到：

赞收藏

资料库

一种改进的永磁同步电机模型预测控制.pdf

相关推荐

开发技术

热门标签

最新资料