第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
失真度测试仪.doc
方案一：同步采样
利用被测信号的倍频信号作为采样时钟进行采样。该方法保证了采样时钟与被测信号的严格同步，避免了采入信号
失真度测试仪
马玖凯 李朋朋 罗怡
摘要：本系统以单片机 AT89C55 和 FPGA 芯片 EP1C6Q240C8 为控制和处理核
心，基于频谱分析的原理，使用不同的 AD 采样芯片，采用直接采样和等效采样
相结合的方式，运用 FFT（Fast Fourier Transform）算法在单片机内进行 FFT 运
算，实现了对不同信号失真度的测试。被测信号频率为 1Hz~1MHz，测得绝对误
差在 1%以内，尤其是 500kHz 以内的低频信号，绝对误差可达 0.4%。系统采用
键盘输入，128×64 点阵液晶显示输出，人机交互灵活，界面友好，操作简单。
关键词：
失真度
直接采样
等效采样
FFT
一、方案论证与选择
1.总体方案
方案一：滤波法
由失真度的定义可知，测量一个波形的失真度，其本质就是将其基波和谐波
分开，分别计算功率。可以设计一个低通滤波器，将谐波滤除，由基波功率和总
功率计算失真度；或者设计一个高通滤波器，将基波滤除，由谐波功率和总功率
计算失真度。
方案二：频谱分析法
用 AD 将信号采入，得到有限长序列。对这些离散点进行 FFT 运算，各次谐
波的幅值，从而计算失真度。
方案一的两种滤波方法本质相同，其思路简单，易于理解，但滤波器的实现
难度较大，对硬件电路的要求很高。而方案二采用数字方法，测量范围广，误差
小，只是在 AD 采样上存在难点，所以我们选择方案二。
2.倍频方案
方案一：FPGA 内部倍频
将被测信号用等精度测频法测出其频率，在 FPGA 内部用频率合成的方法产
生其 2N 倍频（低频段 128 倍频，高频段 32 倍频）的信号。
方案二：硬件锁相环电路倍频
利用锁相环芯片，结合整形电路和分频电路，将信号频率倍到原来的 32 倍。
方案一主要在 FPGA 内部完成，硬件电路少，但精度无法达到很高，且数字
时钟分辨率有限，不能对信号进行连续测量；方案二可获得高速稳定的时钟作为
AD 采样的控制信号，且误差稳定，但由于 32 倍频，能处理的信号频率范围有
限。两种方案各有千秋，我们将两种方案都尝试了，并且都实现了。
3.采样方案
方案一：同步采样
利用被测信号的倍频信号作为采样时钟进行采样。该方法保证了采样时钟与
被测信号的严格同步，避免了采入信号周期不完整而引入的误差，适用于频率不
太高的情况。
方案二：等效采样
取样点来自于信号的若干个周期的不同位置。每一个周期内等效地等间隔地
抽取少量的样本，最后将多个周期抽取的样本集合到同一个周期内，这样就可以
等效成在一个被测信号周期内采样效果。该方案本质为用低频才高频，适用于频
率较高的周期信号。
由于被测信号频率范围宽，所以我们采取两种方案结合的方式。低频段用同
步采样，高频段用等效采样。用锁相环实现时，由于采样信号频率始终为被测信
号的 32 倍，所以用同步采样。
二、理论分析与计算
1.失真度
假设某一信号基波功率为 E1，总功率为 E0，第 i 次谐波分量的幅度为 Ui，则
该信号的失真度为：
THD
E
1
E
0
E
1
UU
2
2
2
3
U
2
U
n
1
（式 2-1）
N 的取值越大，计算值与理论值越接近，误差越小。当 n 趋近于无穷时，计
算值将没有误差，但这在实际中无法实现。我们将 n 取到 64，将足以忽略误差。
][
kX
1
N
n
0
kn
NW
（式 2-2）
FFT 是 DFT 的快速算法，式 2-2 为 DFT 的计算公式，可得到信号的幅度谱。
为旋转因子。测出每个有效点上对应谱线的幅度，
/2
j
其中，0≤k≤N-1，
利用式 2-1，便可计算出信号的失真度。
eW
N
N
2.频谱混叠
信号处理中，时域抽样在频域中相当于信号频谱以抽样频率为周期向两边周
期延拓，即频谱搬迁。在搬迁的过程中，就有可能出现频谱混叠。
对于频谱有限的信号，当抽样频率不足信号最高频率的 2 倍（奈圭斯特频率）
时，就会出现频谱混叠现象，造成较大误差；对频谱无限的信号，如方波，频谱
混叠将无法消除。
此时，提高抽样频率可以减弱混叠。我们将采样率设置为被测信号最高频率
的 128 倍（低频段）或 32 倍（高频段），可有效减弱混叠现象。同时，由于采样
率满足奈圭斯特频率的要求，对频谱有限信号进行采样时，将不会出现混叠现象。
3.频谱泄漏
我们研究的信号是时域无限的。利用 FFT 对此信号进行分析时，需截取一有
限范围，相当于对时域信号加了一个矩形窗，在频域上则相当于其频谱与无限长
的抽样函数卷积。其频谱会从原有频率扩展开来，即能量从单个频谱传播到许多
DFT 频率位置上，造成“泄漏”。
矩形窗在时域的突变导致频域拖尾严重，收敛很慢。通常，用矩形窗截断会
产生较大的泄露，改用相对旁瓣幅度较小的窗可减小泄露。但是，由于被测信号
均为周期信号，只要保证采得的信号为整数个周期，扩展的谱线将正好落在抽样
函数的过零点位置，不会造成泄漏。我们采取的 128 或 32 倍频抽样可实现。
4.栅栏效应
FFT 或 DFT 的结果实际上就是在一组离散的频率上观察加窗的时间无限信号
的频谱，就像透过“栅栏”观察一样，有的地方“透过”，有的地方被“挡住”。在被
“挡住”的频点上，无论有没有谱分量，都不会显示出来。这就是“栅栏”效应。
当采样频率一定时，增大 DFT 长度可使样本谱线加密，而包络保持不变，从
2
而可以使丢失的频谱分量小一些。为此，我们采用 512 点的 FFT 运算。
三、系统整体设计方案及实现
如图 3-1 所示为系统实现的整体框图。
先用锁相环电路将信号 32 倍频，作为 MAX1425 的采样时钟，进行同步采样。
将比较器整形后的信号送入 FPGA 内的测频电路中，测出其频率，并通过
FPGA 内部倍频，得到 LTC1412 的采样时钟。1Hz~10kHz 的低频段信号进行 128
倍频，采取同步采样；10kHz~1MHz 的高频段信号进行 32 倍频，采取等效采样。
图 3-1 系统整体框图
信号采入后，在 MCU 中进行 512 点的 FFT 运算，根据其频谱计算失真度。
四、主要功能模块电路设计
1.模拟部分
(1) 锁相倍频电路
74HC7046 是高速 CMOS 器件，内含线性电压控制振荡器（VCO），两个相
位比较器（PC1，PC2）和一个锁定鉴测器（LOCK DETECTOR），它对方波的锁
相效果比较好，而且上升沿越陡，倍频输出的信号越稳定
我们选取此芯片，在前级用比较器 LM311 整形，形成陡峭的上升沿，并在
后级用 74LS393 进行 32 分频。倍频信号可在 2MHz 到 20MHz 内稳定。电路如
图 4-1。
、
(2) 采样电路
图 4-1 锁相环倍频电路
3
L
D
1
P
C
1
o
u
t
2
C
O
M
P
i
n
3
V
C
O
o
u
t
4
I
N
H
5
C
1
A
6
C
1
B
7
G
N
D
8
V
C
O
i
n
9
D
E
M
o
u
t
1
0
R
1
1
1
R
2
1
2
P
C
2
o
u
t
1
3
S
I
G
i
n
1
4
C
l
d
1
5
V
c
c
1
6
3
.
6
k
分
频
信
号
1
8
0
p
F
1
0
p
F
1
0
0
4
.
7
u
F
1
2
p
F
5
0
+
5
V
1
3
B
A
L
/
S
T
B
6
B
A
L
5
V
-
4
2
7
V
+
8
L
M
3
1
1
1
0
0
n
F
1
u
F
-
1
2
V
1
k
I
n
p
u
t
1
0
k
1
0
0
n
F
1
u
F
1
2
V
5
0
0
5
V
+
5
V
O
u
t
p
u
t
3
2
分
频
L
D
1
P
C
1
o
u
t
2
C
O
M
P
i
n
3
V
C
O
o
u
t
4
I
N
H
5
C
1
A
6
C
1
B
7
G
N
D
8
V
C
O
i
n
9
D
E
M
o
u
t
1
0
R
1
1
1
R
2
1
2
P
C
2
o
u
t
1
3
S
I
G
i
n
1
4
C
l
d
1
5
V
c
c
1
6
7
4
H
C
7
0
4
6
1
C
L
K
1
1
C
L
R
2
1
Q
A
3
1
Q
B
4
1
Q
C
5
1
Q
D
6
G
N
D
7
1
Q
D
8
2
Q
C
9
2
Q
B
1
0
2
Q
A
1
1
2
C
L
R
1
2
2
C
L
K
1
3
V
c
c
1
4
7
4
L
S
3
9
3
MAX1425 是 MAXIM 公司的一款 10 位并行输出、20M 采样率的高性能 AD。
同步采样，图 4-2。
图 4-2 MAX1425AD 采样
LTC1412 是 Linear 公司的一款 12 位并行输出、3M 采样率的高性能 AD。用
该芯片进行采样电路如附录图 4-3。
2.数字部分
选用 FPGA 芯片 EP1C6Q240C8 完成数字部分的设计。
FPGA 内部主要功能模块有：采样控制模块，完成 LTC1412 和 MAX1424 的
采样控制；测频和倍频模块，测出信号频率,并合成倍频信号。如图 4-4 所示为测
频模块电路，其原理见附录图 4-5。
图 4-4 FPGA 内测频模块
五、系统功能测试
1.系统测试仪器
Tektronix TDS 1002 双信道数字示波器
SG1040 数字合成信号发生器
2.测试方法、结果及分析
我们用 SG1040 数字合成信号发生器作为信源，分别输出正弦波、三角波、
方波作为被测信号。用我们制作的测试仪测试这些信号的失真度，记录结果。
SG173SB3 直流稳压稳流电源
DT9205A 数字万用表
4
7
2
3
4
6
M
A
X
4
3
0
5
E
S
A
5
0
+
5
V
-
5
V
5
0
2
2
p
F
C
L
K
O
E
+
5
V
+
5
V
0
.
1
u
F
0
.
1
u
F
0
.
1
u
F
0
.
1
u
F
0
.
1
u
F
A
G
N
D
1
A
V
D
D
2
R
E
F
P
3
R
E
F
I
N
4
R
E
F
N
5
C
M
L
6
A
G
N
D
7
A
V
D
D
8
I
N
P
9
I
N
N
1
0
C
M
L
P
1
1
C
M
L
N
1
2
C
L
K
1
3
O
E
/
P
D
1
4
D
9
1
5
D
8
1
6
D
7
1
7
D
6
1
8
D
5
1
9
D
V
D
D
2
0
D
G
N
D
2
1
D
V
D
D
2
2
D
G
N
D
2
3
D
4
2
4
D
3
2
5
D
2
2
6
D
1
2
7
D
0
2
8
M
A
X
1
4
2
5
+
5
V
0
.
1
u
F
1
2
C
O
N
3
0
2
3
3
0
3
3
0
0
P
1
[
1
0
.
.
1
]
I
n
p
u
t
表 2-1 是用 MATLAB 计算出来的典型信号的失真度。
表 2-1 典型信号的失真度
正弦波
方波
失真度理论值
0％
48.342％
三角波
12.12％
正弦波失真度测试数据见表 5-1，其余波形数据见附录表 5-2、5-3。
表 5-1 测试正弦波失真度数据表（理论值为 0%）
100
0.18545
%
100k
0.20452
%
500
0.19175
%
200k
0.29679
%
0.2044% 0.21476
%
400k
300k
0.50319
0.71421
1k
%
5k
%
10k
0.21078
%
500k
0.82788
%
波形
10
%
50k
%
800k
0.18382
0.20824
0.21813
0.10798
0.15571
50
%
60k
%
1M
1
%
20k
0.11524
%
600k
60k
0.31544
1.0911% 1.4114% 1.8102%
100k
0.33813
200k
0.30908
300k
0.34209
400k
500k
0.4644% 0.42701
600k
0.40118%
%
%
%
%
从这些数据中可以看出，在 FPGA 内倍频控制 LTC1412 采样时，低频段测出
的失真度误差较小，高频段效果不是很理想；用锁相环控制 MAX1425 采样时，
测出的失真度稳定，尤其在高频段，效果更好。
六、总结分析与结论
%
系统采用数字频谱分析法，利用 512 点的 FFT 运算，分析各种各样输入的信
号，计算其频谱。输入信号最高频率可达 1MHz。尤其利用锁相环倍频时，可得
到 2MHz~20MHz 的时钟信号。
测试结果在高频段不理想，尤其是用 FPGA 进行倍频的时候。可能是因为
FPGA 倍频只能用数字合成的方式，精度无法做得很高。频率越高，偏差越大，
导致测得信号失真度的误差也逐渐增大。
锁相环倍频时测得的失真度稳定，但误差也是存在的，主要可能是由于电路
传输延时的原因，导致倍频出来的采样时钟信号和被测信号不能严格同步造成
的。
同时，信号源给出的信号也不是理想的信号，其固有失真度与理论值也会有
一定的差距。
附录一 参考文献
[1] 马忠梅等（编著）.单片机的 C 语言应用程序设计（第 4 版）.北京：北京航空航天
大学出版社，2007.1
2006.
[2] 夏宇闻（编著）.数字系统设计——Verilog 实现（第 2 版）.北京：高等教育出版社，
[3] 阎石（主编），清华大学电子学教研组（编）.数字电子技术基础（第 5 版）.北京：
高等教育出版社，2006.5（2007 年重印）
[4] 李朝青（编著）.单片机原理及接口技术（第 3 版）.北京：北京航空航天大学出版
社，2005.9
2007.7
[5] 林凌，李刚（编著）.实用电子技术 1000 问.北京：电子工业出版社，2008.9
[6] 谢自美（主编）.电子线路设计·实验·测试（第二版）.武汉：华中理工大学出版社，
5
[7] 高吉祥（主编）.基本技能训练与单元电路设计.北京：电子工业出版社，2007.5
[8] （美）米特拉（Mitra，S.K.）著.数字信号处理——基于计算机的方法（第 3 版）.
北京：电子工业出版社，2006.6
附录二 电路原理图
图 4-3 LTC1412AD 采样
图 4-5 等精度测频电路
附录三 完整测试数据
表 5-1 测试正弦波失真度数据表（理论值为 0%）
1.0911% 1.4114% 1.8102%
60k
0.31544
%
100k
0.33813
%
200k
0.30908
%
300k
0.34209
%
500k
400k
0.4644% 0.42701
%
600k
0.40118%
6
0.20824
0.21813
0.18382
1
%
20k
0.11524
%
600k
10
%
50k
0.10798
%
800k
50
%
60k
%
1M
0.15571
100
0.18545
%
500
0.19175
%
1k
0.2044%
0.21476
5k
%
10k
0.21078
%
100k
0.20452
%
200k
0.29679
%
300k
0.50319
%
400k
0.71421
%
500k
0.82788
%
A
I
N
+
1
A
I
N
-
2
V
r
e
f
3
R
e
f
C
o
m
p
4
A
G
N
D
5
D
1
1
(
M
S
B
)
6
D
1
0
7
D
9
8
D
8
9
D
7
1
0
D
6
1
1
D
5
1
2
D
4
1
3
D
G
N
D
1
4
D
3
1
5
D
2
1
6
D
1
1
7
D
0
1
8
O
G
N
D
1
9
O
V
d
d
2
0
D
V
d
d
2
1
D
G
N
D
2
2
C
O
N
V
S
T
'
2
3
C
S
'
2
4
B
U
S
Y
'
2
5
V
s
s
2
6
D
V
d
d
2
7
A
V
d
d
2
8
I
n
p
u
t
+
2
.
5
V
1
0
u
F
O
u
t
p
u
t
O
u
t
p
u
t
+
5
V
1
0
u
F
1
0
u
F
-
5
V
+
5
V
1
0
u
F
1
u
F
A
I
N
+
1
A
I
N
-
2
V
r
e
f
3
R
e
f
C
o
m
p
4
A
G
N
D
5
D
1
1
(
M
S
B
)
6
D
1
0
7
D
9
8
D
8
9
D
7
1
0
D
6
1
1
D
5
1
2
D
4
1
3
D
G
N
D
1
4
D
3
1
5
D
2
1
6
D
1
1
7
D
0
1
8
O
G
N
D
1
9
O
V
d
d
2
0
D
V
d
d
2
1
D
G
N
D
2
2
C
O
N
V
S
T
'
2
3
C
S
'
2
4
B
U
S
Y
'
2
5
V
s
s
2
6
D
V
d
d
2
7
A
V
d
d
2
8
L
T
C
1
4
1
2
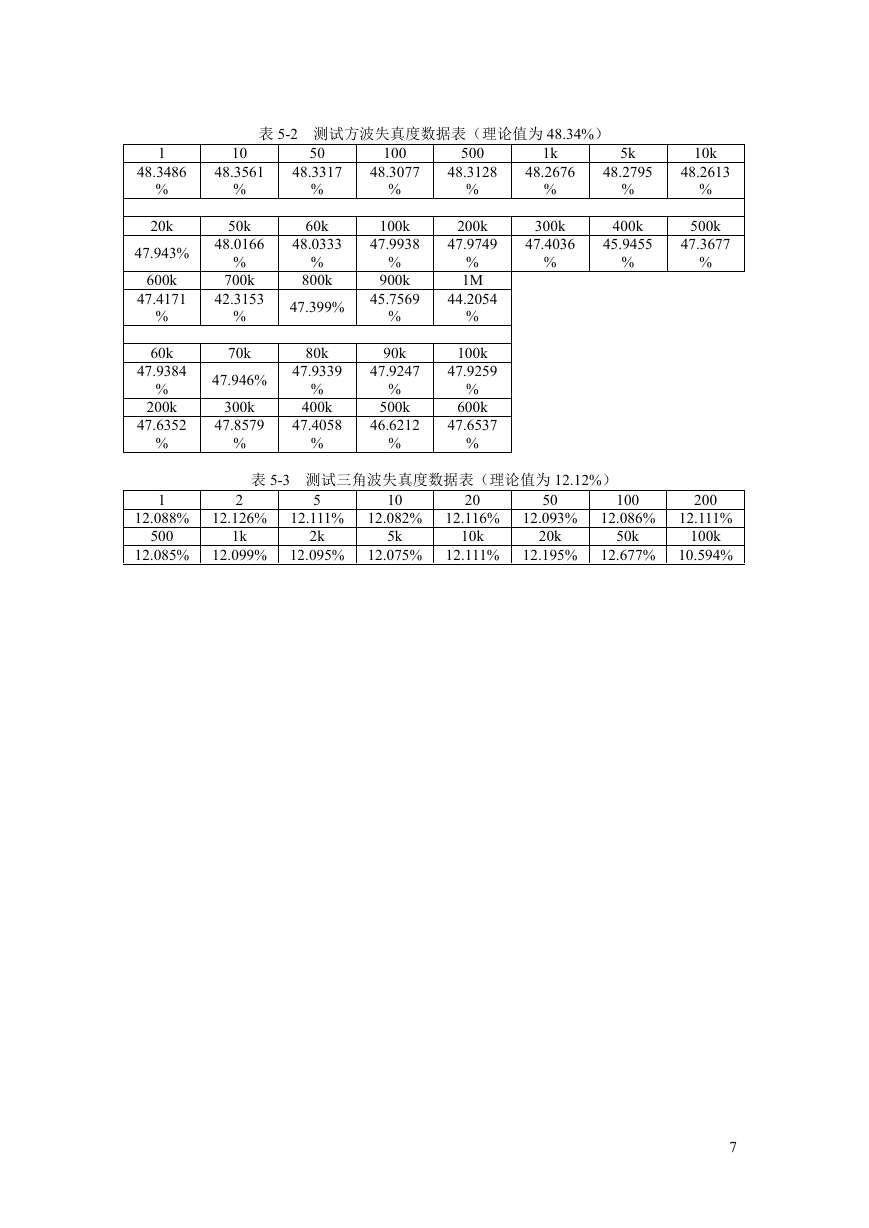
表 5-2 测试方波失真度数据表（理论值为 48.34%）
48.3486
1
%
10
%
48.3561
48.3317
50
%
100
48.3077
%
20k
50k
47.943% 48.0166
%
700k
600k
42.3153
47.4171
%
%
60k
48.0333
%
800k
47.399%
100k
47.9938
%
900k
45.7569
%
500
48.3128
%
200k
47.9749
%
1M
%
44.2054
48.2676
48.2795
5k
%
10k
48.2613
%
1k
%
300k
47.4036
%
400k
45.9455
%
500k
47.3677
%
60k
47.9384
%
200k
47.6352
%
70k
47.946%
300k
47.8579
%
80k
47.9339
%
400k
47.4058
%
90k
47.9247
%
500k
46.6212
%
100k
47.9259
%
600k
47.6537
%
表 5-3 测试三角波失真度数据表（理论值为 12.12%）
12.088% 12.126% 12.111% 12.082% 12.116% 12.093% 12.086% 12.111%
10
5k
20
10k
50
20k
100
50k
200
100k
1
500
2
1k
5
2k
12.085% 12.099% 12.095% 12.075% 12.111% 12.195% 12.677% 10.594%
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
