A New Meta-Baseline for Few-Shot Learning.docx

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：1.43M 资料格式：docx 举报版权申诉

qq_38900441-12555117-4744300845218286735.docx.pdf-第1页.png

第1页 / 共15页

qq_38900441-12555117-4744300845218286735.docx.pdf-第2页.png

第2页 / 共15页

qq_38900441-12555117-4744300845218286735.docx.pdf-第3页.png

第3页 / 共15页

qq_38900441-12555117-4744300845218286735.docx.pdf-第4页.png

第4页 / 共15页

qq_38900441-12555117-4744300845218286735.docx.pdf-第5页.png

第5页 / 共15页

qq_38900441-12555117-4744300845218286735.docx.pdf-第6页.png

第6页 / 共15页

qq_38900441-12555117-4744300845218286735.docx.pdf-第7页.png

第7页 / 共15页

qq_38900441-12555117-4744300845218286735.docx.pdf-第8页.png

第8页 / 共15页

文本预览

对于小样本学习的一个新的元基线摘要：近些年来元学习成为对于小样本学习的流行框架，目的是从小样本分类任务的集合中学习模型。尽管一些越来越多的元学习模型正在出现，我们的研究揭示了一些被忽略的简单基线，提出了一种元基线方法，在所有基类上预训练一个分类器，在最近中心基于小样本学习分类算法进行元学习，它大大超过了最近的最先进的方法（sota）。为什么这个简单的方法效果这么好？在元学习阶段，我们观察到，从基类中更好地推广不可见任务的模型可以降低来自新类的任务的性能，表明潜在的客观差异。我们发现，预训练和从预先训练的分类器继承一个好的小样本分类度量对于元基线是重要的，这可能有助于模型更好地利用具有更强可转移性的预训练代表。此外，我们研究了什么时候在这个元基线需要元学习。我们的工作为这一领域建立了一个新的坚实的基准，并为进一步理解对于小样本学习的元学习框架中的现象提供了线索。 1、介绍：虽然人类已经表现出难以置信的能力，从很少的例子中学习，然后推广到许多不同的新例子，目前的深度学习方法仍然依赖于大规模的训练数据，为了模仿这种人类的泛化能力。小样本学习(Fei-Fei 等人，2006 年；Vinyals 等人，2016 年)被提出用于训练深度网络，以理解一个新的概念，基于少量标注样本，因为直接学习大量的参数与很少的样本是非常具有挑战性的，而且很有可能导致过拟合，一个实际的解决是应用迁移学习。我们可以先在有足够样本的公共类（基类）上训练深度模型，然后将模型转移到仅基于少数几个例子的新类上学习。元学习框架的小样本学习遵循学会学习的关键思想。具体来说，它从属于基类的训练样本中提取少量的学习任务，并优化模型以在这些任务上表现良好。一个任务通常采用 N-way 和 K-shot 的形式，其中包含 N 个类，每个类中具有 K 支持样本（训练集）和 Q 查询样本（验证集）。目的是在学习了 N×K 支持样本后，将这些 N×Q 查询样本成功分类为 N 个类。在元学习框架下，对模型进行直接优化，使其在小样本任务上表现良好。基于这一思想，最近的工作集中在改进元学习结构，而小样本学习本身已经成为评价元学习算法的常见测试平台。越来越多

的元学习方法用于小样本学习，但改进这些基线方法中很少有效果的。我们首先采用一个简单而有效的基线进行小样本学习，我们将这个基线命名为分类器-基线，在分类器-基线中，我们首先在基类上预先训练一个分类器来学习视觉表示，然后删除最后一个依赖于类的全连接(FC)层。给定一个具有少量样本的新类，我们计算给定样本的平均特征，并利用特征空间中的余弦距离，用最近质心对查询样本进行分类即余弦最近质心。这一过程也可以看作是估计新类的最后 FC 权重，但不需要为新类训练参数。虽然在(Chen 等人，2019 年)中也做了类似的尝试，但他们为新的类微调了一个新的 FC 层，并遵循了与 sota 方法不同的设置。相反，我们没有遵循它们，仅简单使用了最近的质心度量，并使用标准的 Image Net 样优化设置来训练我们的模型，从而提高了模型的效率和性能。图 1 ，本文提出了简单而有效的分类器 - 基线和元 - 基线。从 1a 开始，我们观察到 Meta-Baseline 优于元学习，特别是在深层主干中还有大数据集。在 1b 所示的 Meta-Baseline 的元学习阶段，我们观察到当模型更好地推广到基类中不可见的任务时，它的小样本分类执行在新类中的 CE 可以减少，这表明元学习框架中存在客观差异。我们观察到这个分类器-基线的性能与许多最近最先进的元学习方法相当，甚至优于许多最先进的元学习方法，尽管它既没有优化到很少的任务作为元学习或有额外的微调。我们能让元学习实际上改善分类器基线吗？在本文中，我们认为分类预训练和元学习都有自己的优势对于小样本学习，我们提出了 Meta-Baseline 将这两者的优势进行了简单结合。在 Meta-Baseline 中，我们使用预先训练的分类器-基线初始化模型，并使用余弦最近轮廓度量执行元学习，这是在 Clsifier-Baselin 中的评估度量。经验上，我们观察到 Meta 基线可以进一步提高分类器-基线的性能，如图 1a 所示，由于 Meta-基线可以学习与预先训练的分类器-基线的最小变化，

因此在不同的数据集上这个改进是稳定的。鉴于这些令人鼓舞的结果，我们还观察到训练过程中的测试性能下降，因此我们在实验中进一步进行烧蚀分析。我们在元学习的背景下评估了两种泛化类型： 1、基类泛化；是指基类中不可见数据对小样本分类任务的泛化，它遵循泛化的共同定义，但我们将其重命名为澄清；2、新类泛化；表示从新类中的数据中对小样本分类任务的泛化，这进一步表明了从基础类到新类的可转移性。在不同的训练迭代过程中，我们发现，虽然 Meta-Baseline 正在改进基类泛化，但它的新类泛化在降低，这表明：1、在元学习阶段可能是一个客观的差异，改进基类泛化可能导致更糟糕的新类泛化。2、由于模型是在元学习之前预训练，分类前训练可能为元学习模型提供了额外的可转移性。3、当新类更类似于基类时元学习相对于分类符-基线的优势更加明显。在我们的进一步实验中，我们得到了一致的观察，支持这些假设。总之，我们的贡献如下：· • 我们提出了一个简单的 Meta-Baseline，它兼具分类预训练和元学习的优点，并且在很大程度上优于 sota。 • 我们观察到基类泛化和新类泛化之间的不一致性，这可能会回顾元学习中要解决的关键挑战，用于小样本分类。 • 我们研究了数据集方面（类相似性、尺度)和骨干方面(模型大小）的因素如何影响元学习相对于分类器-基线的优势。 2、相关工作：小样本学习的目标是在只有少数标注样本的情况下使分类模型适应新的类。早期尝试(Fei-Fei 等人，2006 年)建议利用以前课程中学到的知识，并采用贝叶斯实现。最近的几次小样本学习方法大多遵循元学习框架，该框架用小样本任务从训练数据中抽样来训练模型。在此框架下，设计了各种用于小样本学习的元学习架构，大致可以是分为三种主要类型：基于内存的方法、基于优化的方法和基于度量的方法。

图 2。分类器-基线和 Meta-基线。在 Classifier-Baseline 中，我们在所有基类上预先训练一个分类模型，并删除其最后一个 FC 层以获得编码器 fθ。给定一个小样本任务，我们计算了支持集中每个类的样本的平均特征，然后用具有余弦相似度的最近质心方法对查询集中的样本进行分类。在 Meta-Baseline 中，我们进一步选择在其评估算法上对一个预先训练的分类器-基线进行了成像，并引入了一个额外的参数τ来缩放余弦相似度。基于内存的方法：基于内存（记忆）的方法的关键思想是训练一个具有记忆的元学习者来学习新的概念。(Ravi&Larochelle，2017)建议用一个基于 LSTM 的元学习器去学习小样本优化算法。(Munkhdalai 等人，2017 年)根据特定任务的信息对网络的激活值进行更改。在(Santoro 等人，2016 年)，一类特定利用记忆增强的神经网络被用于元学习。 (Mishra 等人，2018 年)提出了一种使用时间卷积和软结合的简单神经注意元学习器。在 MetaNet(Munkhdalai&Yu，2017)中，提出了一种快速参数化方法来学习跨任务的元级知识。基于优化的方法：另一项工作遵循的想法是在元学习框架内将优化过程与支持集区分开来。 MAML(Finn 等人，2017 年)找到一个初始化的神经网络，可以使用几个优化步骤适应任何新的任务。(Grant 等人，2018 年)重新制定了 MAML，以便在贝叶斯框架内进行概率推理。 LEO 模型(Rusu 等人，2019 年)遵循与 MAML 相似的思想，通过执行基于梯度的元学习学习低维潜在空间，克服了低数据状态下高维参数空间的过拟合问题。 MetaOptNet(Lee 等人，2019 年)旨在学习能够很好地推

广用于线性支持向量机(SVM)分类器的特征表示。基于度量的方法：除了明确考虑动态学习过程外，基于度量的方法元学习了特征空间中具有度量的深度表示。匹配网络(Vinyals 等人，2016)用余弦距离计算注意值，对查询样本进行分类，并提出了一个全上下文编码模块(FCE)，该模块对查询样本的权重进行了条件化整个支持集跨类设置。原型网络(Snell 等人，2017 年)遵循一个类似的想法，他们计算支持集中每个类的平均特征，并通过最近的质心方法对查询样本进行分类它们用一个 Bregman 散度的平方欧氏距离代替余弦相似度。关系网络(Sung 等人，2018 年)通过提出一个关系模块进一步概括了这一框架作为一种可学习的度量，与深度表示联合训练。 (Oleshkin 等人，2018 年)建议使用任务条件度量，从而产生与任务相关的度量空间。虽然元学习框架取得了显著进展，但最近的一些工作研究了预先训练的分类器的性能。 (Gidaris&Komodakis，2018 年)评估经过余弦度量训练的分类器，表明该分类器的性能优于以往的几种元学习方法。(Chen 等人，2019 年)对两个分类器进行研究，在特征空间中分别用线性分类器和余弦度量训练的分类器，它们选择为小样本任务微调一个新的 FC 层，与以前的元学习模型相比表明它可以达到竞争的效果。虽然这些工作将预先训练的分类器的变体与以前的几种元学习方法进行比较，然后提出了更先进的工作(Rusu 等人，2019 年；Sun 等人，2019 年； Lee 等人，2019 年)，建立了新的最先进的结果（sota）。我们提出的 Meta-Baseline 采用了最简单形式的预训练分类器和元学习的优点，它的性能优于以往最先进的方法，并证明了它的有效性和用于小样本学习的元学习框架的潜在问题。

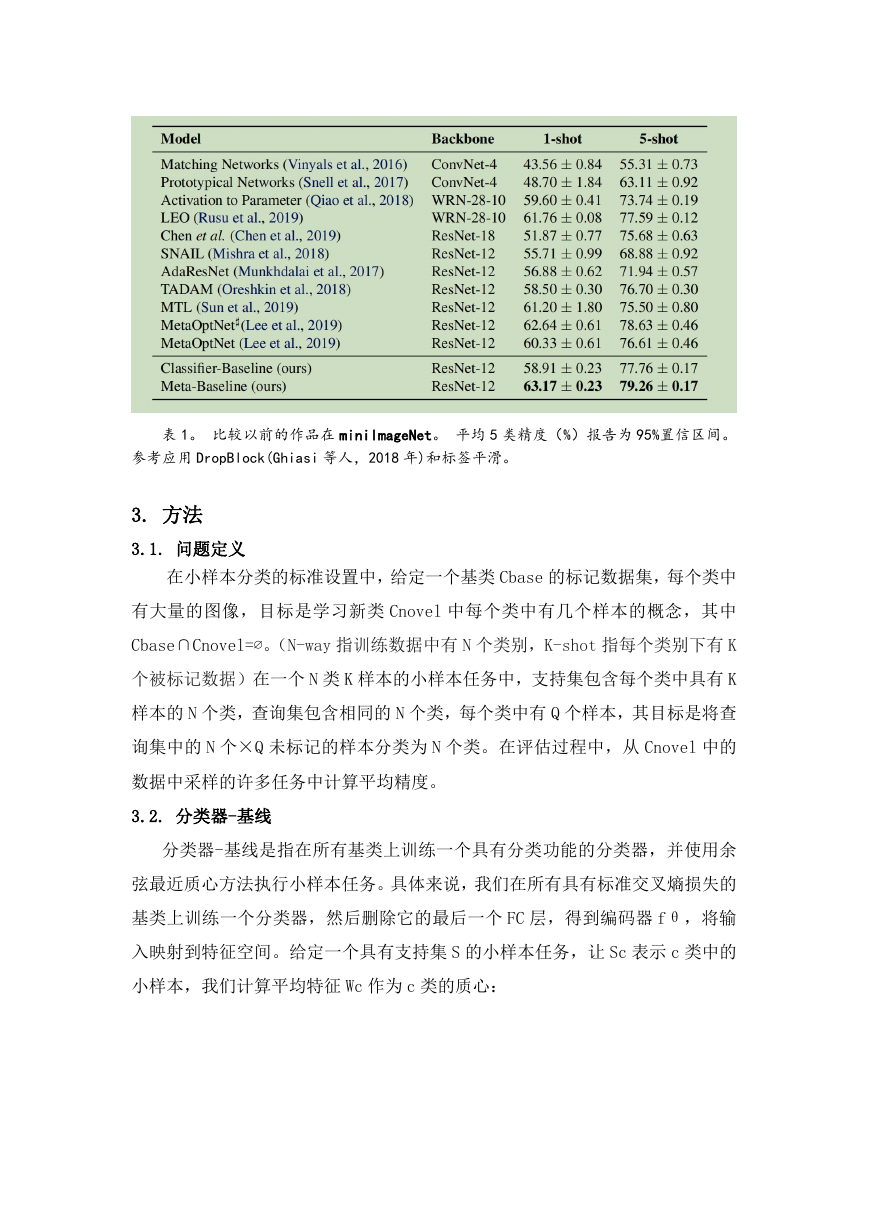
表 1。比较以前的作品在 miniImageNet。平均 5 类精度（%）报告为 95%置信区间。参考应用 DropBlock(Ghiasi 等人，2018 年)和标签平滑。 3. 方法 3.1. 问题定义在小样本分类的标准设置中，给定一个基类 Cbase 的标记数据集，每个类中有大量的图像，目标是学习新类 Cnovel 中每个类中有几个样本的概念，其中 Cbase∩Cnovel=∅。（N-way 指训练数据中有 N 个类别，K-shot 指每个类别下有 K 个被标记数据）在一个 N 类 K 样本的小样本任务中，支持集包含每个类中具有 K 样本的 N 个类，查询集包含相同的 N 个类，每个类中有 Q 个样本，其目标是将查询集中的 N 个×Q 未标记的样本分类为 N 个类。在评估过程中，从 Cnovel 中的数据中采样的许多任务中计算平均精度。 3.2. 分类器-基线分类器-基线是指在所有基类上训练一个具有分类功能的分类器，并使用余弦最近质心方法执行小样本任务。具体来说，我们在所有具有标准交叉熵损失的基类上训练一个分类器，然后删除它的最后一个 FC 层，得到编码器 fθ，将输入映射到特征空间。给定一个具有支持集 S 的小样本任务，让 Sc 表示 c 类中的小样本，我们计算平均特征 Wc 作为 c 类的质心：

然后，对于小样本任务中的查询样本 x，我们预测样本 x 属于 c 类的概率作为样本 x 的特征向量与 c 类质心之间的余弦相似度：其中<.,.>表示两个向量的余弦相似度。请注意，Wc 也可以看作是新 FC 层对新概念的预测权重。 3.3. Meta-Baseline 图 2 说明了 Meta-Baseline 方法。一般来说，Meta-Baseline 包含两个培训阶段。第一阶段是训练前阶段，即训练分类器基线法(即基线法。在所有基类上训练分类器，并删除其最后一个 FC 层以获得 fθ)。第二阶段是元学习阶段，我们在分类器-基线评估算法上对模型进行优化。具体来说，给定预先训练的特征编码器 fθ，我们从基类中的训练数据中采样 N 类 K 样本任务(具有 N×Q 查询样本) 为了计算每个任务的损失，在支持集中，我们计算定义的 N 个类的质心在方程 1 中，然后用于计算方程 2 中定义的查询集中每个样本的预测概率分布。损失是由 p 和查询集中样本的标签计算的交叉熵损失。请注意，我们将每个任务视为训练中的数据点，每个批可能包含多个任务，并计算平均损失。表 2。对比以往在分层图像网上的工作。平均 5 路精度（%）报告 95%置信区间。 *指(Lee

等人，2019 年)的结果) 缩放余弦相似度：由于余弦相似度具有[-1,1]的值范围，当它用于计算 logits 时，在训练过程中应用 Softmax 函数之前，对该值进行缩放是非常重要的。我们增加了一个可学习的参数τ类似于最近的工作(Gidaris&Komodakis，2018 年；Qi 等人，2018 年； Oreshkin 等人，2018 年)，预测的训练概率为：在我们的实验中，我们观察到这种设计选择对于提高模型性能也很重要。 4.实验 4.1 数据集 miniImageNet 数据集(Vinyals 等人，2016 年)是小样本学习的共同基准。它包含从 ILSVRC-2012 抽样的 100 个类(Russakovsky 等人，2015 年)，然后将其随机分为 64、16、20 个类，分别作为训练、验证、测试集。每个类包含 600 个大小为 84×84 的图像。我们遵循(Lee 等人，2019 年)的发布。分层图像网数据集(Ren 等人，2018 年)是最近提出的另一个具有更大规模的通用基准。它是 ILSVRC-2012 的一个子集，包含来自 34 个超级类别的 608 个类然后将其分成 20、6、8 个超级类别，分别产生 351、97、160 个类作为培训、验证、测试集。图像大小为 84×84。请注意，此设置更具挑战性，因为基类和新类来自不同的超级类别。我们进一步提出了一个新的数据集 Image Net-800 来测试我们的方法，它是从 ILSVRC-2012 年 1K 类中派生出来的，通过随机分割 800 个类作为基类，200 个类作为新类。这个基类包含原始训练集中的图像，新类包含原始验证集中的图像。我们提出了这个数据集，用于更大规模的实验，并根据图像分类任务制定设置标准(He 等人，2016 年)。注意，在这个数据集中没有验证拆分，因为类差异可能导致客观差异，如我们的实验所示，根据验证集选择模型可能会为模型比较带来额外的偏差。 4.2. 实现细节

分享到：

赞收藏

资料库

A New Meta-Baseline for Few-Shot Learning.docx

相关推荐

人工智能

热门标签

最新资料