第1页 / 共130页
第2页 / 共130页
第3页 / 共130页
第4页 / 共130页
第5页 / 共130页
第6页 / 共130页
第7页 / 共130页
第8页 / 共130页
2020美赛特等奖B题论文.pdf
2007698
Introduction
Problem Background
Literature Review
Our work
Preparation of the Models
Analysis of Problems
Assumptions
Notations
The Optimal 3D Geometric Shape
Model Preparation
Model Principle
Model Assumption
Model Construction
The Rules
The Steps of the Algorithm
Estimation of P and M
Result
The Optimal Sand-to-Water Mixture Proportion
Model Preparation
The Principle of Model
The Steps of Algorithm
Result
The Optimal Shape in Rainy Day
Modified CA Model
Model Assumption
Similarities and Difference from Basic Model
The Steps of Algorithm
Result
Sensitivity Analysis
Strengths and Weaknesses
Strengths
Weaknesses
Promption
Strategies to Make sandcastle More Lasting
Conclusion
Article
References
Appendix: Our Code
2010821
1.Introduction
1.1Background
1.2 Restatement of the Problem
2.Assumption and Justification
3.Glossary and Notation
3.1 Glossary
3.2 Notation
4.Optimal Shape Model Based on Sandcastle Foundation
4.1 Model Overview
4.2 Quantitative model of sand-bearing capacity
4.3 Sandcastle Foundation dynamics equation model
4.4 Solution of Sandcastle Foundation Dynamics Eq
4.4.1 Solution of Cuboid Dynamics Simulation
Step1. Initialize the parameters of the sandcastle
4.4.2 Simulation solution of dynamics equations of
4.5 Geometric Shape Solving Model Based on Discret
4.5.1 Model Overview
4.5.2 Model establishment and solution
5. Optimal water and sand ratio model
5.1Model Overview
5.2 Quantitative model of Water and sand polymeriz
5.3 Solving the Model
6.Fuzzy comprehensive evaluation model based on ra
6.1 Model Overview
6.2 Evaluation model for rain erosion resistance
6.2.1 Establishment of Model
6.2.2 Solution of Model
6.3 Optimal Shape Fuzzy Comprehensive Evaluation M
6.3.1 Establishment of Model
6.3.2 Solution of Model
7. Humidity Prediction Model Based on RBF Neural N
7.1 Model Overviw
7.2 Model Preparation
7.3 RBF neural network algorithm
8.Sensitivity Analysis
8.1 Sensitivity Analysis of Most Shaped Model Base
8.2 Sensitivity Analysis of Optimal Water-Sand Mix
8.3 Sensitivity Analysis of A Fuzzy Comprehensive
8.4 Sensitivity Analysis of Sandcastle warning pro
9. Evaluation and Promotion of Model
9.1 Strength and Weakness
9.1.1 Strengths
When using the RBF neural network algorithm, we ha
9.1.2 Weaknesses
9.2 Promotion
10. Conclusions
References
Memo
Appendix
2011873
2013836
2019696
1 Introduction
1.1 Background
1.2 Restatement of the Problem
2 Analysis of the problem
1
1
2
2.1 Literature Review
2.2 Problem Analysis
3 Assumptions and Justifications
4 Notations
2
3
2
3
3
4
5 Model and Solution
4
5
1
2
3
4
5
5.1 Sandcastle-Erosion Model
1
2
3
4
5
5.1
5.2 Solution to Optimal Water-to-Sand Mixture Proportion
5.3 Sandcastle-Rain-Erosion Model
5.2
6 Advice on Building a Sandcastle
5
6
7 Sensitivity Analysis
6
7
8 Strengths and Weakness
7
8
8.1 Strengths
.1
8.2 Weakness
Article for Fun in the Sun
References
Appendix
8
9
9
10
Problem Chosen
B
2020
MCM
Summary Sheet
Team Control Number
2007698
A Simulation Based Assessment of Sandcastle
Foundation
Summary
Sandcastle building is a common way to recreating for beach goers. Sand lovers
always rack their brains to build a stronger castle and take pride in it. Still, sandcas-
tle is inevitably eroded by the waves and tides. Therefore, how to establish a stable
foundation is of great significance to the duration of sand castles.
In order to explore the most stable three-dimensional geometric shape, we establish
a periodic sand-water cell automaton model to experiment with the most likely mul-
tiple geometric shapes. We discretize the sand base into a three-dimensional geometry
consisting of a stack of rigid sand cells and water cells. Based on the knowledge of
engineering mechanics and the feasibility in practice, we select five types of inertial
frustum which has significant characteristics: triangular frustum, square frustum, six-
arris frustum, conical frustum, ellipse frustum and so on for simulation experiments.
The optimum geometric shape we obtain is triangle frustum.
In the model, we formulate the state transition rules through multivariate analy-
sis based on multi-criteria judgments, and carry out quantitative calculations on the
waves’ sediment carrying and capillary phenomena between sand and water. We em-
ploy complex trigonometric functions to simulate and reproduce the tidal waves in
three dimensions. Therefore, through regression analysis of the data obtained from
multiple experiments on each frustum, we have obtained a reliable and optimal geo-
metric shape result. Besides, it can be quantified and visualized.
In the practice of building sand castles, it was found that different sand-to-water
mixture ratios also played a crucial role in the sand foundations’ stability. By using
the sand-water cell automaton model of problem 1, we use the concentration gradi-
ent method to adjust the water-sand ratio and obtain a series of data points on the
sand-to-water proportion and the sand-based stability. Then we use the least squares
polynomial function approximation to fit the curve of these data. Therefore, we obtain
an estimated function of sand-to-water ratio and sand-base stability. Then we can find
that the optimal sand-to-water mixture proportion is 0.55.
In order to study rain’s effect on the result, we introduce a rainfall module based
on the original model.
It will work on the sandy base with the wave tide module.
Similarly, we get a series of data for regression analysis. We find that the original best
geometry does not the only one which perform well under rainfall conditions, and
ellipse frustum is the another better geometry when it is rainy.
Sensitivity analysis shows the strong robustness of our model. Meanwhile, we also
propose some other strategies for increasing the stability of the sandy base. Subse-
quently, we summarize the experimental models and conclusions into plain language
for publication on Fun in the Sun.
In addition, our model is easy to implement and extend. By changing few parame-
ters in our code, we can stimulate more complex conditions on the beach.
Keywords: periodic sand-water cell automaton model, multivariate analysis, quantified
and visualized, concentration gradient method
1
Introduction
1.1 Problem Background .
.
1.2 Literature Review .
1.3 Our work .
.
.
. .
. .
.
.
2 Preparation of the Models
2.1 Analysis of Problems .
.
2.2 Assumptions .
2.3 Notations .
. .
.
.
.
. .
.
.
.
.
Contents
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 The Optimal 3D Geometric Shape
3.1 Model Preparation .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1 Model Principle . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2 Model Assumption . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.3 Model Construction . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.4 The Rules
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.5 The Steps of the Algorithm . . . . . . . . . . . . . . . . . . . . . .
3.1.6 Estimation of P and M . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. .
.
.
.
.
.
.
.
.
.
3.2 Result .
4 The Optimal Sand-to-Water Mixture Proportion
4.1 Model Preparation .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.1 The Principle of Model . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.2 The Steps of Algorithm . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Result .
.
.
.
.
.
.
.
.
.
.
.
5 The Optimal Shape in Rainy Day
.
.
5.1 Modified CA Model .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.1 Model Assumption . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.2
Similarities and Difference from Basic Model . . . . . . . . . . . .
5.1.3 The Steps of Algorithm . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Result .
.
.
.
.
.
.
.
.
.
6 Sensitivity Analysis
7 Strengths and Weaknesses
.
.
.
7.1
Strengths . .
7.2 Weaknesses
7.3 Promption .
. .
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
8 Strategies to Make sandcastle More Lasting
9 Conclusion
Article
References
Appendix: Our Code
2
2
2
3
3
3
4
4
5
5
5
5
6
6
8
8
9
11
11
11
11
12
13
13
13
13
13
14
16
17
17
18
18
18
19
20
21
23
Team # 2007698
1
Introduction
1.1 Problem Background
Page 2 of 29
Playing is the nature of human, but it is not easy to get some kind of inspiration
while playing. There are castles of various shapes on the beach, either simple or deli-
cate. Even under the same condition, some castles can be maintained for a long time,
while some castles can’t withstand a wave and disappear without a trace. How to
make our castles more durable is a question that most poeple are curious about. There
are many factors which influence the firmness of sandcastles, such as sand-to-water
mixture proportion, the type of sand, weather etc.
In this paper, we attempt to explore a three-dimensional geometric model of a sand-
castle foundation having the best stability. First, we need to build a mathematical mod-
el that analyzes the optimal three-dimensional geometry shape. Second, based on this
model, we are required to consider the optimal sand-to-water mixture proportion to
achieve the best adhesion between the sands. Furthermore, taking the impact of the
weather into consideration, we need investigate the optimal 3D geometric shape once
again.
1.2 Literature Review
Since the last century, the interaction between water and sediment has been the
focus of scholars in related fields. They have carried out a large number of experiments
and researches to explore water-sand interactions and their effects on stability.
Sandpile problem. Mason, TG and Levine, AJ and Erta¸s, D and Halsey, TC (1999)[11]
had studied the critical angle of wet sandpiles. Dumont, Serge and IGBIDA, Noured-
dine (2009) [4] based on implict Euler dicretization in time, improved formula in Prigozhin
model.J.P. Bouchaud, J.-P. and Cates, M. E. and Prakash, J. Ravi and Edwards, S. F.
(1995) [1] propose a new continuum description of the dynamic of sandpile surfaces
and found a "spinodal" angle at which the surface of sandpile will be unstable. Du-
mont, Serge and Igbida, Noureddine (2011)[5] analysed this problem by using the col-
lapsing model introduced by Evans.
Sediment mathematical model. Emiro˘glu, Mehmet and Yalama, Ahmet and Er-
do˘gdu, Yasemin (2015)[6] explored the ratio of the water and the clay/sand to study
the material’s satablity. Then they found the optimal ratio was between 0.43 and 0.66.
Gröger, Torsten and Tüzün, Ugur and Heyes, David M (2003)[8] used CDEM to mea-
sure od cohesion in wet granular materials and proved Rumpf’s equation’s genaral
agreement.
Slope stability. "Slope stability is one of the basic problems in geotechnical mechan-
ics and engineering." Research on this topic is significant for river and traffic safety. Af-
ter reviewing literatures, we find that the mainstream analysis method is still around
the traditional three methods: limit equilibrium, limit analysis and numerical analy-
sis method. These three methods are kind of a generalization from two-dimensional
to three-dimensional space, and thus have various limitations(Gao, Wang & Zhang,
2009[15]). Futhermore, more and more literatures have begun to consider changes in
slope stability under different weather conditions(Yeh, Lee & Chang, 2020[14]; Chen,
Liu & Li, 2020[2]). In this paper, we employ cellular automata, etc.
Team # 2007698
Page 3 of 29
Sandcastle problem. Halsey, Thomas C and Levine, Alex J (1997)[9] thought the
capillary force significantlly affect the sandpiles’ stability and the critical angle is costan-
t in the limit of large system. Then they analyzed the reason why sandcastle will fall.
Coincidently, at the same year, Hornbaker, DJ and Albert, Réka and Albert, István
and Barabási, A-L and Schiffer, Peter (1997) [10] expored why sandcastles can stand
and drew the conclusion that wetting liquid can change the properties of qranular me-
dia resulting in a great increase of citicle angle. Fraysse, N and Thomé, H and Petit,
L(1999) [7] also explored the influence of humidity on the castles’ stability. Recent year,
Pakpour, Maryam and Habibi, Mehdi and Møller, Peder and Bonn, Daniel(2012) [12]
demonstrated how to build the perfect castle from the prospect of sandcastles’ height.
The sandcastle foundation has the same principle as the slope stability, and relate
to above several problems. There are varying methods to deal with simlilar problems.
Inspired by cell automaton, We hope to provide a new solution to the study of slope
stability through the sandcastle foundation model.
1.3 Our work
Under the assumption that castles are built at roughly the same distance from the
water on the same beach with the same type and amount of sand. We establish a model
based on cellular automata to formulate the problem.
˜Task 1 We use periodic cellular automaton to simulate the environment of the sand-
castle to find the optimal 3D model. We suppose several most likely geometric
shapes as alternative shape. Then we formulate State Transition Rules through
multivariate analysis based on multi-criteria judgments. By running the cellu-
lar automaton several times, we explore the most stable shape of the sandcastle
foundation.
˜Task 2 We address the problem of optimal sand-to-water mixture proportion by fit-
ting function of the lasting time and sand-to-water proportion. Based on the
3D geometric shape we sort out in Task 1, we adjust the ratio accourding to the
concentration gradient method. Record the duration of the model with differ-
ent sand-to-water ratio. The longest lasting sandy foundation’s sand-to-water
proportion is the target value we anticipate.
˜Task 3 Considering the effect of rainfall, we adjust our cellular automaton and repeat
the procedure in Task 1. Then we find out the optimal 3D geometric shape in
this case.
2 Preparation of the Models
2.1 Analysis of Problems
Different from the analysis of the sandpile problem, the sand castle on the beach is
the result of mixing water and sand. On one hand, with the degree of sand adhesion
increases, the stability of the sand castle will increase. On the other hand, the sand
castle will also be affected by external forces. Continuously being eroded by the waves
and tides, will accelerate the destruction of the sand castle. Therefore, we need to find a
model that can comprehensively consider the impact of two aspects on the sandcastles.
Team # 2007698
2.2 Assumptions
Page 4 of 29
We make the following assumptions about our Cellular Automaton Simulation Pro-
cess:
• The sandcastle foundation is only a mixture of sand and water, and all air has
been exhausted. In reality, it is impossible for us to turn the inside of the sand
pile into a vacuum with bare hands. For the accuracy of the experiment, the
sandcastle foundation used is carefully designed so that all the air in the sand-
water mixture can be considered exhausted.
• The side of the sandcastle foundation is sloped. The stability of the triangle
shows that the sloped side has higher stability.
• Only the damaging effect of the waves on the surface of sandcastle founda-
tion is considered. In fact, there are both waves and tides having an influence
on the surface and structure. However, we do not consider the structural dam-
age caused by the waves. Because people usually build sand castles at a certain
distance from the sea, and the side of the slope is enough to greatly reduce the
impact of the waves on the sandcastle.
• The sandy base is stable. Sandcastle foundation will not collapse by the non-
wave factor.
• The waves will not change the water-sand mixture ratio of the sandcastle foun-
dation, but will only corrode the foundation from the surface. The mixture of
sand and water has a capillarity phenomenon, and the surface of the sand base
can block most of the water from entering the interior.
• Sea waves take sand from the surface of sandy bases with their maximum ca-
pacity for sand transport.The relationship between sediment content and sedi-
ment transport capacity is expressed by Dou Guoren’s equation[3]
∂ (hs)
∂t
At the ideal state,we have
+
∂ (hvs)
∂x
+ αω (S − S∗) = 0
∂ (hs)
∂t
+
∂ (hvs)
∂x
= 0
Hence, the sediment transport capacity is equal to the sediment content.
• The beach sand is composed of natural sand, white bakelite sand and brown
bakelite sand. The wave’s sediment carrying capacity of volume Sv is estimated
at 55%[13] on the beach.
Additional assumptions are made to simplify analysis for individuals sections. These
assumptions will be discussed at the appropriate locations.
2.3 Notations
The primary notations used in this paper are listed in table 1.
Team # 2007698
Page 5 of 29
Symbol
Sv
F
Uj
M, m
P
K
L
H
d
Gi
Gmin
tj
σ
Table 1: Notations
Definition
Waves’ sediment carrying of volume
Number of water cells adjacent to sand cells
Number of the water cells around the each surrounding sand cell
Sand-to-water proportion
Boundary conditions for the "fall" of sand cells
Instable factors
Cell space size
Maximum height of sandcastle foundation
Width of sandcastle foundation
Number of the cells on the top of the foudation
= G0
Lasting time of the sand foundation
Stability Coefficient
2 , Collapsed boundary conditions
3 The Optimal 3D Geometric Shape
In this section, we will use cellular automata to simulate the interaction between
sand and water. We do experiment with several simple geometries to find the most
stable one of the sandy base.
3.1 Model Preparation
3.1.1 Model Principle
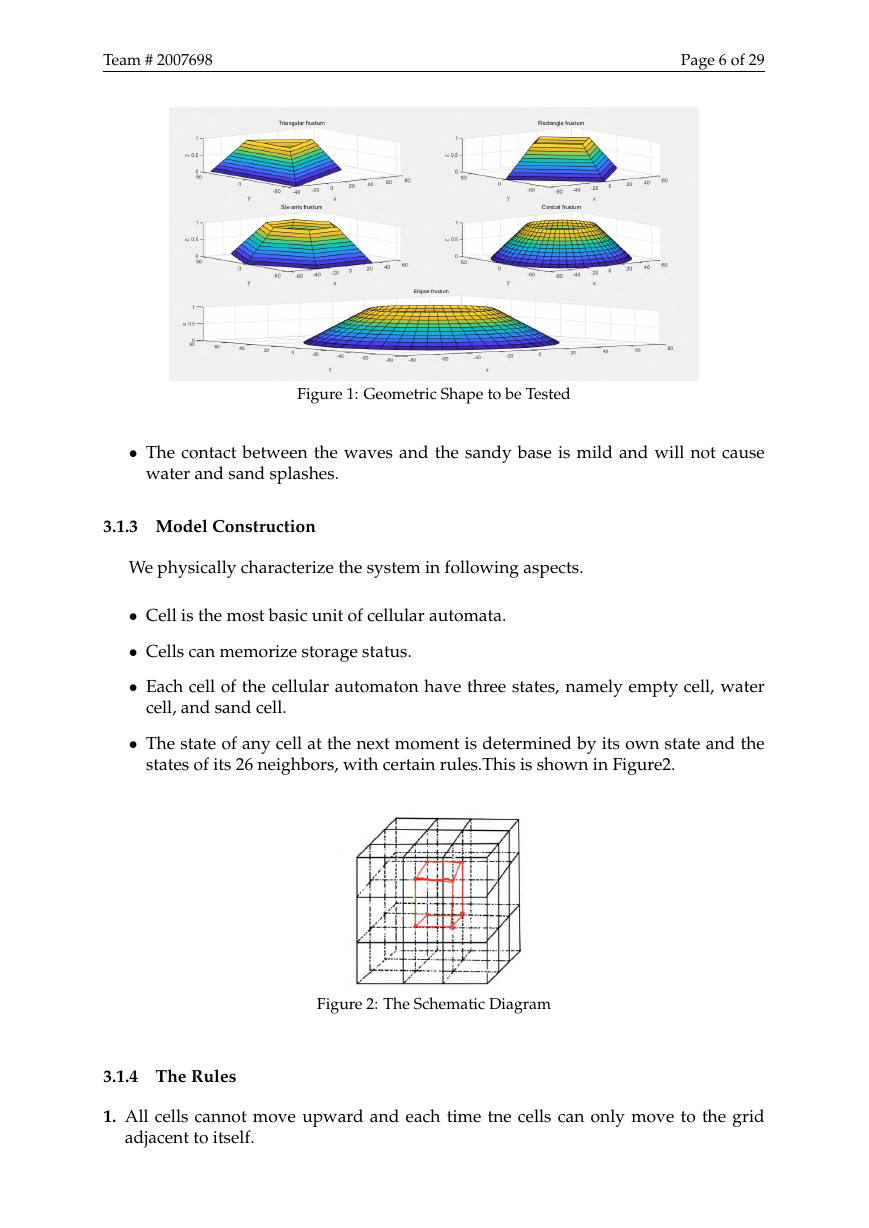
Theoretically, the sandcastle base with a inclined side is the most stable. For a ge-
ometric shape, the arris are the most prominent features of the side. Therefore, We
choose the most representative shape to do experiment, such as triangular, square,
six-arris, conical, ellipse frustum and so on(shown in Figure 1). We carry out several
experiments to study the influence of arris on the stability of sandy bases.
Many complex problems can be modeled by cellular automata. Cellular automaton
is essentially a dynamic system defined in a cell space composed of cells with discrete
and finite states. According to certain local rules, these cells evolve in discrete time
dimensions. The dynamic system has evolved in the time dimension has been widely
applied to various fields of social, economic, military and scientific research.
This model is a periodic cellular automaton model.
3.1.2 Model Assumption
• Both sand and water can be regarded as incompressible particles.
• The sand and water can be mixed together in a certain ratio, and a relatively
stable sand foundation can be built at the same time.
• We do not take water evaporation into consideration.
Team # 2007698
Page 6 of 29
Figure 1: Geometric Shape to be Tested
• The contact between the waves and the sandy base is mild and will not cause
water and sand splashes.
3.1.3 Model Construction
We physically characterize the system in following aspects.
• Cell is the most basic unit of cellular automata.
• Cells can memorize storage status.
• Each cell of the cellular automaton have three states, namely empty cell, water
cell, and sand cell.
• The state of any cell at the next moment is determined by its own state and the
states of its 26 neighbors, with certain rules.This is shown in Figure2.
Figure 2: The Schematic Diagram
3.1.4 The Rules
1. All cells cannot move upward and each time tne cells can only move to the grid
adjacent to itself.
Team # 2007698
Page 7 of 29
2. If there are F (F ≥ P) water cells and n sand cells adjacent to the sand cell, let this
cell’s "instable factor" to be K. Then,
K = F − σ
n∑
j=1
Uj
Where,
K is the stability of the sand cell considering the viscosity between sand and water
Uj is the number of the sand cells around the center sand cell
3. If K ≥ P, the sand cell begin to "move downward" follow the principle:
Sand cells can only move downward or horizontally, and preferentially in the di-
rection downward and with the most water cells. The target position change into a
sand cell, and the original position becomes a water cell.
When the sand cell moves down, the water cell in the middle change first. If the
middle one is not a water cell, both neighboring cell will change in the same proba-
bility.
If there are no water cell below the sand cell, the sand cell will move to the water or
empty cell on its right. Otherwise, move to the cell adhere.
4. If there are less than P water cells adjacent to the sand cell, the state of the cell holds
still.
Figure 3: Transition Rule of Sand and Water Cell
5. If the water cell is adjacent to 15 or more sand cells, the cell keep constant.
6. If there are empty cells below the water cell, the water cell preferentially moves to
the empty cells below with equal probability; if not, the cell moves with equal prob-
ability to other empty cells. After the target cell becomes a water cell, the original
cell becomes empty.
7. "Sea waves" (composed of water cells) appear on the left side of the model with a
certain pattern.
If there is an empty cell to the right of "sea wave", this empty cell will convert into a
water cell(The middle one change first, if the middle one is not an empty cell, both
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
