logo资料库

Mathematica 中文版教程pdf版.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：1.37M 资料格式：pdf 举报 版权申诉
第1页 / 共102页
第2页 / 共102页
第3页 / 共102页
第4页 / 共102页
第5页 / 共102页
第6页 / 共102页
第7页 / 共102页
第8页 / 共102页
资料共102页，剩余部分请下载后查看
    ch0-绪论
    ch1-Mathematica 的基本量
    ch2-初等代数运算
    ch3-微积分
    ch4-线性代数
    ch5-数值计算
    ch6-在Mathematica 中作图
    ch7-定义函数和变换规则
    ch8-程序设计
    绪 论 0.1 符号计算系统简介 数值计算与符号计算 1946 年世界 上 第 一台计 算 机 ENIAC (The Electronic Numerical Integrator and Computer) 是为数值积分服务的。 一提起计算机求解人们立刻想到的是数值求解，这是因为计算机的早期应用范围主 要是数值求解。其实数值求解是计算机求解的一个方面，计算机进行计算的另一方面即 对数学表示式的处理已形成一门新的科学分支，称为符号计算或计算机代数，它是一门 研究使用计算机进行数学公式推导的理论和方法，演算数学公式的理论和算法是它研究 的中心课题。 数值计算： 常量、变量、函数、运算符 --〉数值、字符、逻辑量 表达式 一个值 多 一 近似计算 例：计算 y=sin10+ln10。其结果是 1.75856。 在高级语言中，算术表达式由常量、变量、函数和运算符等组成，算术表达式的 值为某一精度范围内的数值。计算各类表达式的值是高级语言的主要工作。 符号计算(计算机代数): 常量、变量值、函数值 --〉数值、字符、逻辑量 表达式 表达式 多 多 准确计算 x 2 sin xdx ＝ -（-2 + x 2 ）cos x + 2 x sin x ∫ 与数值计算相比，符号计算对计算机硬件和软件提出了更高的要求。 符号计算系统 符号计算系统是一个表示数学知识和数学工具的系统， 一个集成化的计算机数学软件系统。 数值计算、 符号计算、 图形演示 程序设计 公式推导、数值计算和图形可视化操作一致性和连贯性。 符号计算系统的对象从初等数学到高等数学，几乎涉及所有数学学科。包括各种数 学表达式的化简、多项式的四则运算、求最大公因式、因式分解、常微分方程和偏微分 方程的解函数。各种特殊函数的推导、函数的级数展开、矩阵和行列式的各种运算和线 性方程组的符号解等。 和数值计算一样，算法也是符号计算的核心。就算法而言，符号计算比数值计算能 继承更多的更丰富的数学遗产，古典数学家许多算法仍然是核心算法的成员，近代数学 1
    的算法成果也在不断地充实到符号计算中。 符号计算已成功地应用于几乎所有的科学技术和工程领域，其中包括数学理论领 域。由于它和数值计算一样，能够正确地完成人在短时间内无法完成的公式推导计算， 使得不少研究领域的前沿向前推移。 符号计算的应用 验证公式的工具 在十九世纪，法国文学家 Charles Delaunay 计算月亮的位置作为时间函数。从 1847 年到 1867 年用了 20 年的时间，完成并发表了长达数百页的计算方面的文章，推导了近 四万个公式。到 1970 年 MIT 的一个研究小组以 Drprit 为首用符号计算软件对于 Delaunay 的计算公式进行复算，只用了 20 小时的 CPU 便完成了。复算表明原先的计算只有 3 个 错误，其中一个错误是某项的系数是 3 而不是 2，另外两个错误是由此而引起的。这是 一个很有代表性的例子。 例如：一个七个自由度行走的机器人，从运动方程求解加速度时，包括大量的多维 转换公式推导，可以有上百项，甚至上千项。这时只能用符号计算系统才能迅速、准确 的求解，在推导有限元的刚度矩阵中，在计算行列式展开和合并中，都可以用任何一个 符号计算系统来完成公式演算。 用符号计算系统进行公式推导，简单、正确和快速。它帮助科研人员摆脱了理论推 导中繁琐的一面，将精力更多的放在创造性的思维中。 理论研究中的实验方法 在物理、化学和生物学等许多自然科学领域中，实验是科学研究的一个手段。符号 计算系统的出现为数学领域和一些理论研究领域提供了“实验”工具。部分高校的“数 学实验室”应运而生。数学的创造大多来自直觉，用符号计算系统对设想的定理结论直 接验证，将待研究的方程绘出图形以观察变化趋势，会给科研人员带来不同程度的灵感 和启发，甚至会得到意想不到的收获。再将结果进行理论深化并加以严格证明。如今数 学实验已被一些数学工作者所接受。数学实验课程已列入国家教委 21 世纪教学改革的 重点课程之一。 符号计算系统软件简介 符号计算已有几十个软件系统，一般有专用系统和通用系统两类。通用符号计算系 统都具有数值计算、符号计算和图形功能。都有适合于从工作站到微机使用的多种版本。 符号计算语言是这种算法在计算机上的工具。符号计算系统由符号计算语言和若干软件 包组成。目前，典型的通用符号计算系统有：（按字母顺序排列） Axiom Macsyma Maple Mathematica Reduce Derive 符号计算系统通常都有两种运行方式：一种是交互式，每发一个命令，就执行一种 相应的数学计算。 另一种方式是写一段程序，执行一系列的命令，就想用 Fortran 或 C 写程序一样。 每个符号计算系统都有自己的程序设计语言，这些语言与通用的高级语言大同小异。请 看 C 语言和 Mathematica 中的几个语句形式： 2
    C 语 言 Mathematica if（表达式）语句 1 else 语句 2 If [表达式,语句 1, 语句 2] while （表达式）语句 While [表达式,语句] for (初值；终值条件；增量）语句 For [初值，终值条件，增量，语句] 0.2 Mathematica 简介 Mathematica 是 美 国 Wolfram 研 究 公 司 开 发 的 符 号 计 算 系 统 。1988 年 发 布 Mathematica 系统的 1.0 版，因系统精致的结构和强大的计算能力而广为流传，经不断 扩充和修改后，在 1991 年和 1997 年推出了功能更加充实和完善的 Mathematica 2.0 版和 Mathematica 3.0 版，在 1999 年推出了 Mathematica 4.0 版。 Mathematica 是最大的单应用程序之一，它内容丰富功能强大的函数覆盖了初等数 学、微积分和线性代数等众多的数学领域，它包含了数学多方向的新方法和新技术；它 包含的近百个作图函数是数据可视化的最好工具；它的编辑功能完备的工作平台 Notebooks 已成为许多报告和论文的通用标准；在给用户最大自由限度的集成环境和优 良的系统开放性前题下，吸引了各领域和各行各业的用户。 现在 Mathematica 在世界上拥有超过一百万的用户，已在工程领域、计算机科学、 生物医学、金融和经济、数学、物理、化学和社会科学等范围得到应用。尤其在科研院 所和高等院校流行。 目前，至少有 14 种语言写成的 200 多册书籍和几种专门介绍 Mathematica 的期刊。 在英国和日本都有大学将 Mathematica 作为理工科学生入校必修的计算机课程之一。它 也是“数学模型”和“数学实验”课程最好的工具之一。世界各地的大学和高等教育工 作者已开发基于 Mathematica 的多门课程。 Mathematica 是用 C 语言编写的，Mathematica 1.2 版大约有 150,000 行长。它吸取 了不同类型的软件的特点。 ·具有 BASIC 语言的简单易学的交户式操作方式 ·具有 MathCAD, Matlab 那样强的数值计算功能 ·具有 Maccsyma,Maple,Reduce 和 SMP 那样的符号计算功能 ·具有 APL 和 LISP 那样的人工智能列表处理功能 ·像 C 与 PASCAL 那样的结构化程序设计语言 Mathematica 的开发者 Stephen Wolfram 是 Mathematica 的创始人，并公认是当今科学计算的先驱。 Wolfram 1959 年生于伦敦。他在 Eton（伊顿公学）， Oxford（牛津大学）和 Caltech（加 州理工学院）受教育。他在 15 岁发表了第一篇科技论文，于 1979 年 20 岁时在加州理 工学院获理论物理学博士学位。 从 1973 年开始使用计算机，1981 年主持开发了第一个计算机代数系统 SMP。 Wolfram 的研究范围包括了物理学、数学和计算机的许多领域。他早期的工作主要 在能物理、量子场论和宇宙学方面。由于他在物理和计算方面的成绩，1981 年成为最年 轻的麦克阿 （MacArthur）奖学金获奖者。Wolfram 所做的元细胞自动机(cellular automata) 的计算模型应用到数学和物理出现的复杂系统。Wolfram 关于元细胞自动机的工作已在 3
    许多不同的邻域得到广泛的应用，它导致生物学和物理学中图样生成的新模型，以及研 究混沌和随机性的新方法。Wolfram 发明了基于元细胞自动机的快速加密系统。1986 年， 他创办了杂志 Comliex Systems 。担任过伊里诺大学复杂系统研究中心的主任，物理学、 数学和计算机科学教授。 从 Wolfram Research 公司创办开始，Stephen Wolfram 就担任公司的总裁并致力于 Mathematica 的发展，Wolfram 负责 Mathematica 的总体设计，他写了 Mathematica 大部 分的基本核心代码。 DanielR.Grayson 是伊里诺大学的数学教授。他于 1976 年在麻省理工获得数学博士 学位，曾在哥伦比亚大学和高等研究所工作。他写了 Mathematica 的数学部分的许多内 容，包括任意精度的算术运算、解方程、矩阵演算、幂级数和椭圆函数。Grayson 主要 的研究兴趣是代数 K 理论，这个数学分支把代数几何、线性代数和数论的概念结合在一 起。Grayson 广泛地使用计算机研究数论中的猜想。在参加 Mathematica 工作以前， Grayson 开发了一种用于数论研究的交互式计算机系统。 Roman E.Maeder 负责 Mathematica 的符号积分、多项式因式分解和其它多项式运 算。Maeder 于 1986 年在苏黎世高等工艺学院获得博士学位，其论文是关于程序设计语 言的数学理论。从 1983 年起，Maeder 的工作领域是计算机代数及其对数学教育的应用。 他给计算数学研究生开设了“数学实验室”课程。 Stephen M.Omobundro 写了 Mathematica 的三维图形程序代码。Omobundro 于 1985 年在伯克力加州大学获数学物理学博士学位。1985 至 1986 年他曾在 Think Machines 公 司从事大规模并行计算的算法方面的工作。他是 Connection Machine 计算机用的 LISP 语言设计者之一。 0.3 初识 Mathematica Mathematica 是什么？ Mathematica 能做什么？ 希望 Mathematica 会成为你工作和学习中的好伙伴！ 进入 math4.0 在“开始”菜单中的“程序”中单击 ，进入 Mathematica 4.0 之后，得到如下的 Notebook 窗口，并给 Notebook 暂时取名 Untitled-1，直到用户保存时 另命名为止。 假定用户已经掌握 windows 中下列常规操作： 单击：单击鼠标左键；双击：快速地连续击两次鼠标左键； 拖放：按住鼠标左键拖动鼠标。 在文件菜单中保存、打开关闭文件等操作。 图 0 -1 Mathematic 4.0 窗口 4
    退出 math4.0 在“File”菜单中选择“Exit”命令或按“Alt + F4”。如果窗口中还有内容没有保存到 Notebook 中，这时会出现一个对话框，系统要问你是否保存 Notebook，单击对话框上的“否（N）” 按钮则关闭窗口；单击“是（Y）”按钮，则保存 Notebooks 后退出窗口。退出后返回到调 入 Mathematica 以前的状态。 输入和计算表达式 In[1]:= 12345*23456 Out[1]=289564320 （* 像在用一个计算器 *） 运行命令方式：按 Shift+Enter 对 x 3 −12 x 2 −145x+1716 因式分解； In[2]:= Factor[x^3 -12x^2-145x+1716] Out[2]= (-13 + x) (-11 + x) (12 + x) In[3]:= Expand[(x-3)(y^2-x+6)] （* 展开多项式 *） Out[3]= −18 + 9 x − x − 3 y 2 + x 2 y 2 计算 391,561,357 的最大公约数； In[4]:= GCD[391,561,357] Out[4]= 17 In[5]:= LCM[21,29,35] （ * 计算 21,29,35 的最小公倍数 *） Out[5]= 3045 3 ⎧ ⎨ ⎩ y 5 = − 5 + = 解方程组 2 y x x In[6]:= Solve[{3x-2y == 5,x+y == 5},{x,y}] Out[6]= {{x->3, y->2}} dx x 2 sin dx 计算 In[7]:= D[x^2Sin[x],x] Out[7]= x 2 Cos[x] + 2 x Sin[x] 计算不定积分 x 2 sin xdx ∫ In[8]:= Integrate[x^2Sin[x],x] Out[8]= -（-2 + x 2 ）Cos[x] + 2 x Sin[x] 计算定积分 3.1 ∫ 1.1 2 x cos sin 2 + x dx In[9]:=Integrate[(Cos[x]+2)/Sin[x]^2, {x,1.1,1.3}] 5
    Out[9]=0.546958 定义矩阵 AA，AB，AC； In[10]:=AA= {{1,2,3,4},{3,2,5,6},{1,2,-1,2},{0,2,5,7}}； AB= {{7,6,5,4},{8,5,3,2},{9,6,1,8},{0,-3,-4,5}}； AC= {{3,1,2,0},{4,5,0,8},{6,7,1,9},{7,8,2,3}} In[11]:= TableForm[AA.AB+AC] (* 矩阵运算如此简单 ! 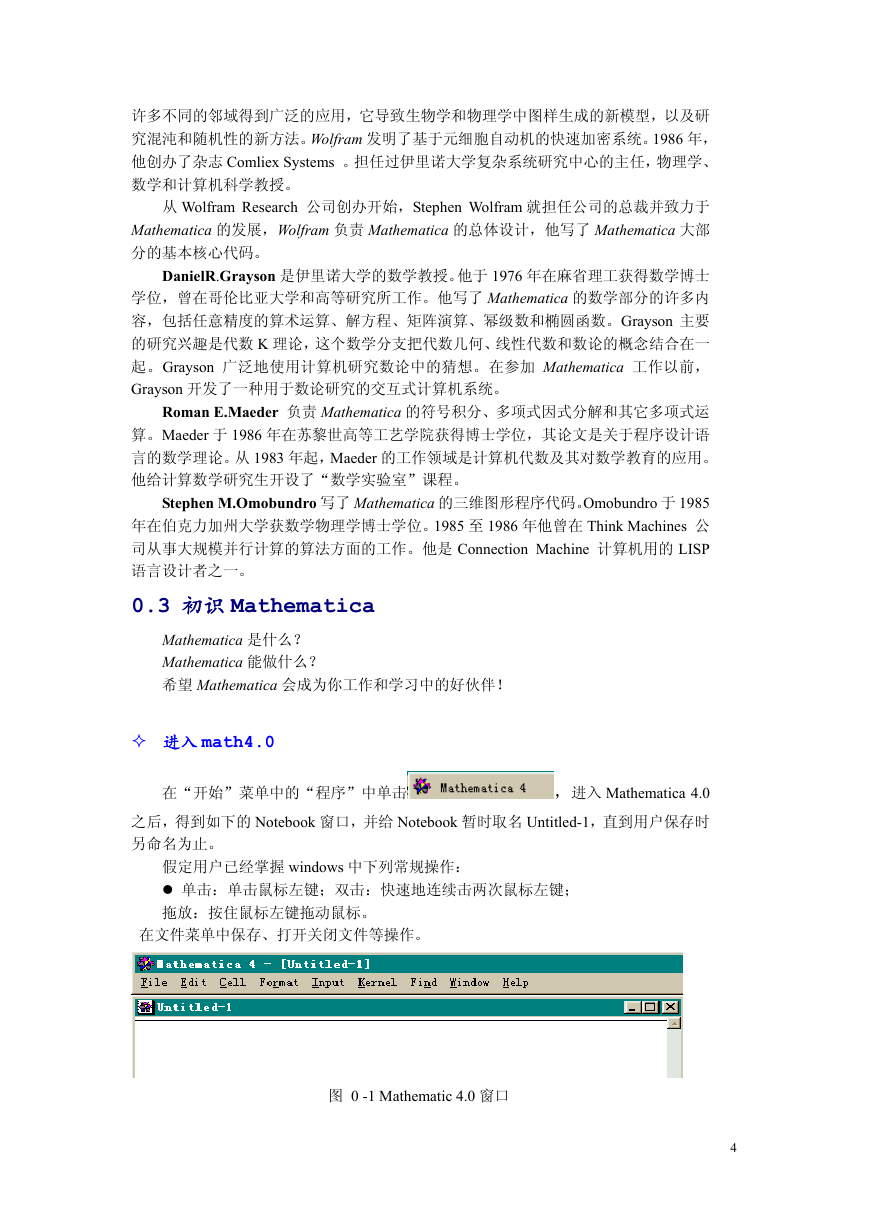*) In[12]:= Plot[x^5-3x+7,{x,-3,3}] 15 12.5 10 7.5 5 2.5 -3 -2 -1 1 2 3 图 0- 3 Out[12]= -Graphics- (* 一个命令，一个图形呼之而出 *) In[13]:= ParametricPlot[{Sin[0.99t]- 0.7*Cos[3.01t], Cos[1.01t]+0.1Sin[15.03t]}, {t,-150,150}, PlotStyle -> RGBColor[0.2, 0.5, 0.3], PlotPoints -> 300, Axes -> None] z 2 x = 画出马鞍面 In[14]:= Plot3D[x^2-y^2,{x,-5,5},{y,-5,5}, ≤≤−≤≤− − y 5,2 5,5 x y 5 BoxRatios -> {1,1,1}] 6
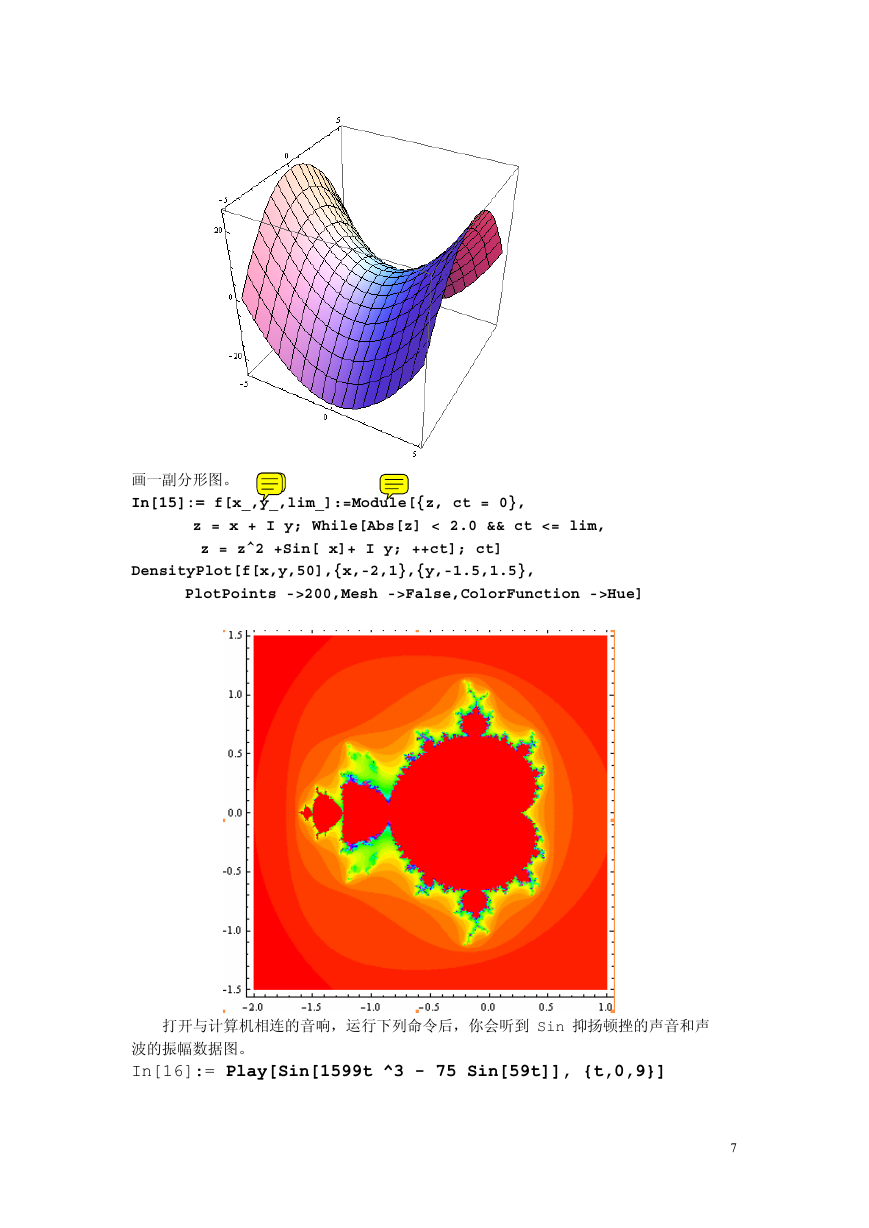
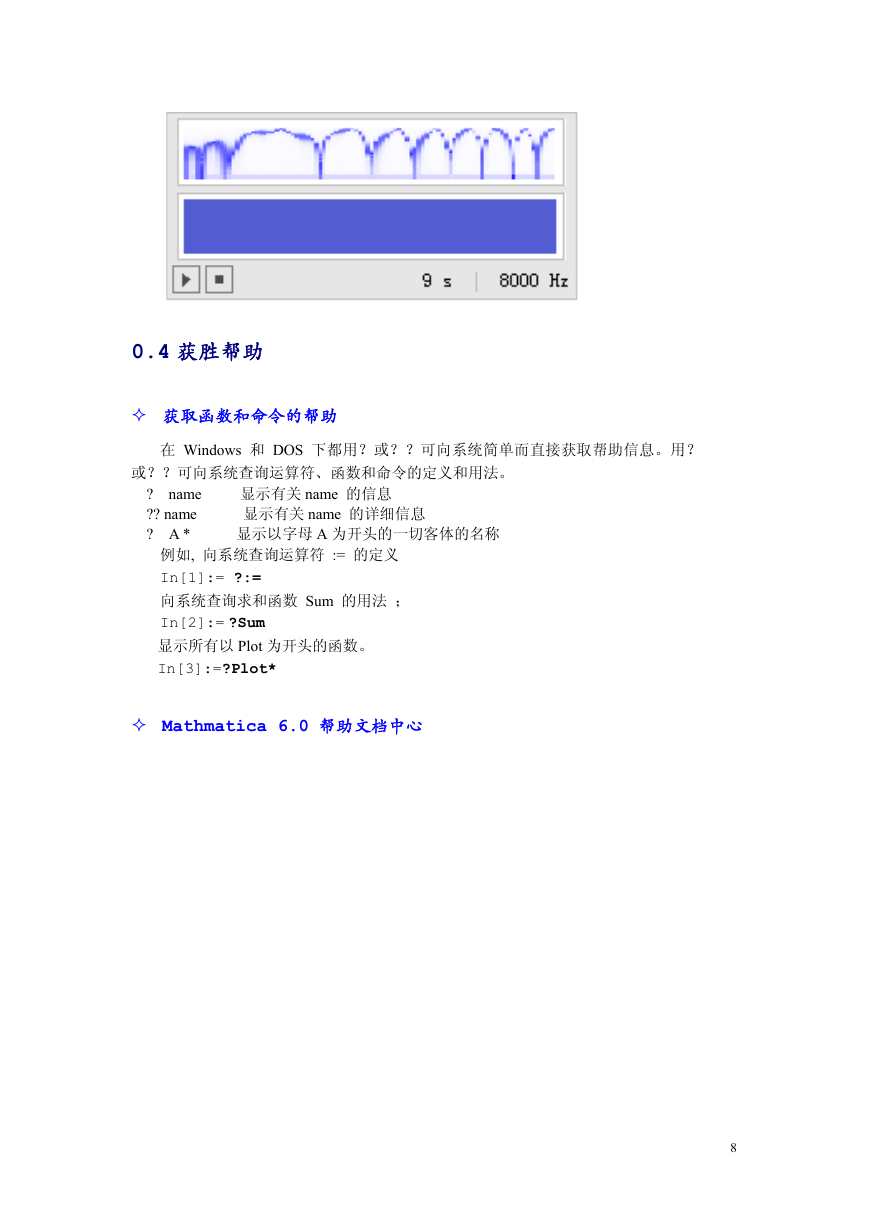
    画一副分形图。 In[15]:= f[x_,y_,lim_]:=Module[{z, ct = 0}, z = x + I y; While[Abs[z] < 2.0 && ct <= lim, z = z^2 +Sin[ x]+ I y; ++ct]; ct] DensityPlot[f[x,y,50],{x,-2,1},{y,-1.5,1.5}, PlotPoints ->200,Mesh ->False,ColorFunction ->Hue] 打开与计算机相连的音响，运行下列命令后，你会听到 Sin 抑扬顿挫的声音和声 波的振幅数据图。 In[16]:= Play[Sin[1599t ^3 - 75 Sin[59t]], {t,0,9}] 7
    0.4 获胜帮助 获取函数和命令的帮助 在 Windows 和 DOS 下都用？或？？可向系统简单而直接获取帮助信息。用？ 或？？可向系统查询运算符、函数和命令的定义和用法。 ? name 显示有关 name 的信息 ?? name 显示有关 name 的详细信息 ? A * 显示以字母 A 为开头的一切客体的名称 例如, 向系统查询运算符 := 的定义 In[1]:= ?:= 向系统查询求和函数 Sum 的用法 ； In[2]:= ?Sum 显示所有以 Plot 为开头的函数。 In[3]:=?Plot* Mathmatica 6.0 帮助文档中心 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料