Butterworth （巴特沃斯）滤波器设计参考.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.59M 资料格式：pdf 举报版权申诉

u010333323-11654143-16359647392981219271.pdf-第1页.png

第1页 / 共9页

u010333323-11654143-16359647392981219271.pdf-第2页.png

第2页 / 共9页

u010333323-11654143-16359647392981219271.pdf-第3页.png

第3页 / 共9页

u010333323-11654143-16359647392981219271.pdf-第4页.png

第4页 / 共9页

u010333323-11654143-16359647392981219271.pdf-第5页.png

第5页 / 共9页

u010333323-11654143-16359647392981219271.pdf-第6页.png

第6页 / 共9页

u010333323-11654143-16359647392981219271.pdf-第7页.png

第7页 / 共9页

u010333323-11654143-16359647392981219271.pdf-第8页.png

第8页 / 共9页

文本预览

1Butterworth（巴特沃斯）滤波器设计参考--ByWater在嵌入式音频产品开发过程中经常会到LPF（LowPassFilter低通滤波器）和HPF（HighPassFilter高通滤波器），一般情况下都是离线用工具(如:Matlab）设计好滤波器的参数（FilterCoefficients）再应用到产品中去。但有些状况下需要用户自己根据需求来实时(Real-time)调整FilterFrequencyResponse(滤波器频率响应）,这种情形下就需要在嵌入式系统中实时根据客户的设定需求来产生相应的FilterCoefficients。下文就汇总出了N阶IIRLPF&HPFButterworth滤波器系数的设计方法，具体的算法原理推导可以参考陈佩青《数字信号处理教程》一书，此处只给出工程上可以应用的结论。背景介绍：归一化的巴特沃斯滤波器系统函数一般形式：NNansasasaadsH22100(Note:参考陈佩青《数字信号处理教程》第二版266页（6-108）表达式)一般情况下会希望保持通带增益为0dB，因此设定d0=a0。在a0=aN=1情况下得到如下归一化的巴特沃斯多项式：N多项式因子12345678(Note:参考维基百科“巴特沃斯滤波器”)

2由此得到d0=a0=aN=1情况下的Butterworth多项式展开的系数表：1,)(0022100daasasasaadsHNNN(Note:参考陈佩青《数字信号处理教程》第二版266页表6-4)上面的表达式是s域的表达式，下面是变化到z域的方法。低通滤波器：sccccffCzzCs/2,12tan111c1111采样频率fs,-3dB频率点fc高通滤波器：1,2tan,111111cccCzzCs（Note:参考陈佩青《数字信号处理教程》第二版291页表6-8）

3其他带通、带阻滤波器频率变换式参考表6-8（下图）

4参考设计：1.1阶ButterworthLPF设计0,11,10,111111)()1()1(11)1(11)(111;11)(2111021110111111111111111111111111111ACCAABCCBBzCCzCCCCzHzCCzCCzCCzzCCzCzzHzzCsssHscccffC/2),2tan(1因此，在确定fc、fs后，1阶的Butterworth滤波器系数就能按照上式计算出来了。如果嵌入式系统没有数据函数库，那么tan的计算方式可以换成tan(x)=sin(x)/cos(x),加入sin/costable后就能计算出sin/cos值了。具体Fixedpoint实现在后续文章再表。

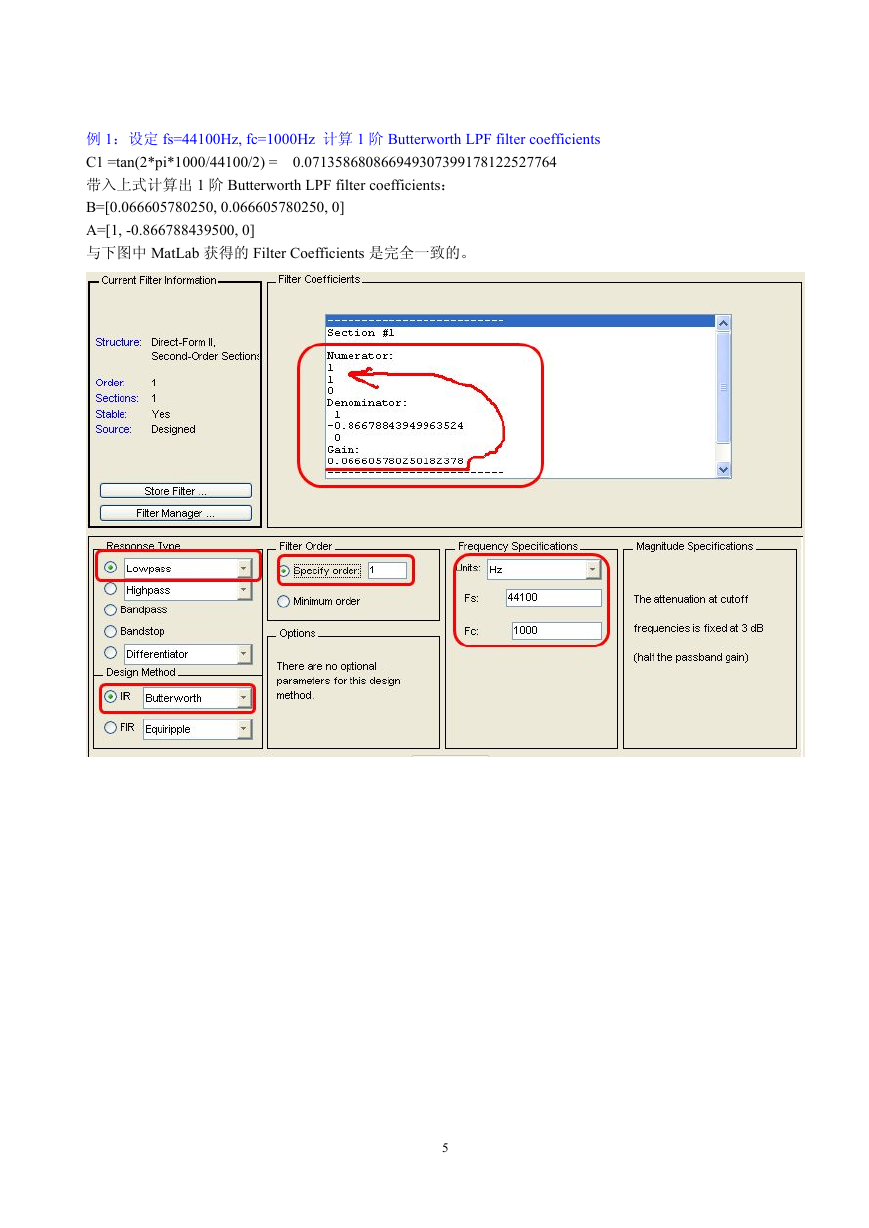
5例1：设定fs=44100Hz,fc=1000Hz计算1阶ButterworthLPFfiltercoefficientsC1=tan(2*pi*1000/44100/2)=0.071358680866949307399178122527764带入上式计算出1阶ButterworthLPFfiltercoefficients：B=[0.066605780250,0.066605780250,0]A=[1,-0.866788439500,0]与下图中MatLab获得的FilterCoefficients是完全一致的。

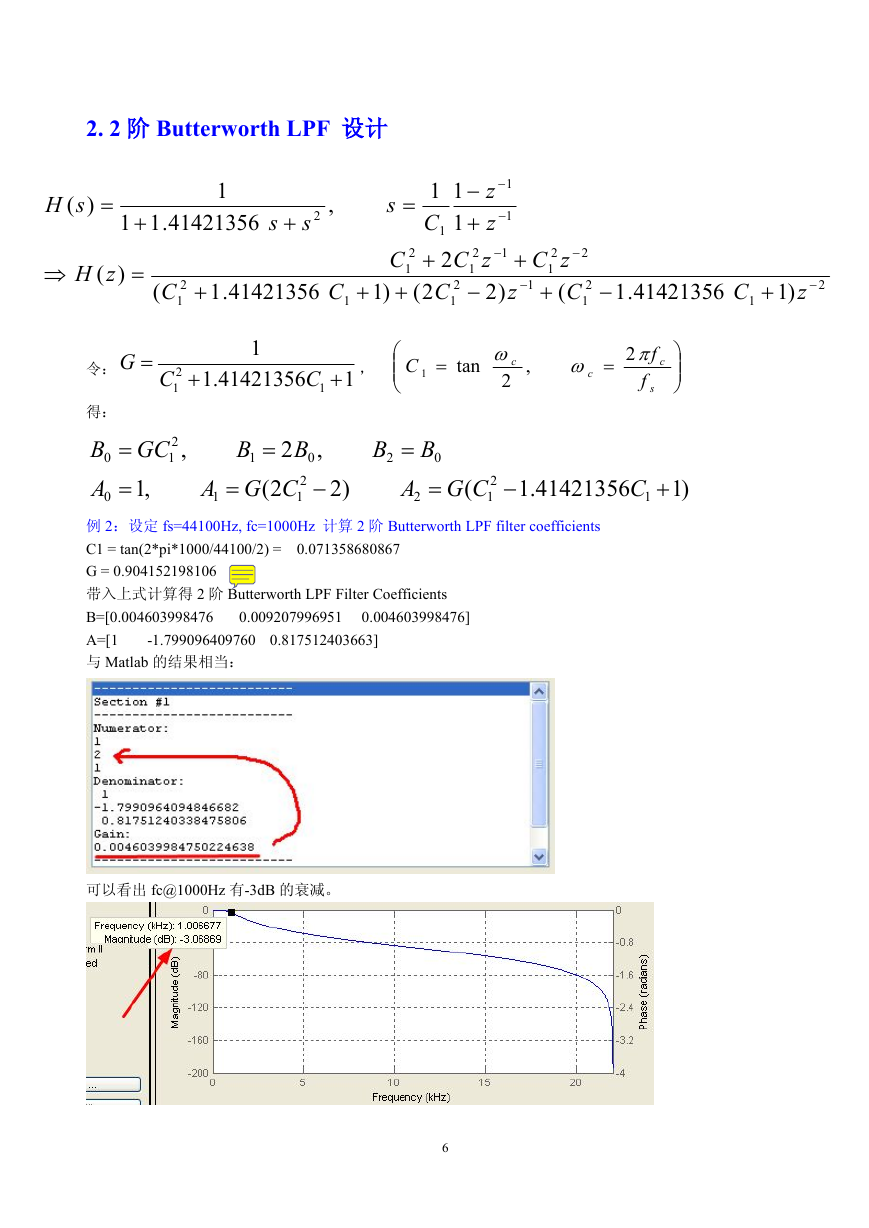
62.2阶ButterworthLPF设计2121121121221121211112)141421356.1()22()141421356.1(2)(111,41421356.111)(zCCzCCCzCzCCzHzzCssssH令：141421356.11121CCG，scccffC2,2tan1得：)141421356.1()22(,1,2,121221100201210CCGACGAABBBBGCB例2：设定fs=44100Hz,fc=1000Hz计算2阶ButterworthLPFfiltercoefficientsC1=tan(2*pi*1000/44100/2)=0.071358680867G=0.904152198106带入上式计算得2阶ButterworthLPFFilterCoefficientsB=[0.0046039984760.0092079969510.004603998476]A=[1-1.7990964097600.817512403663]与Matlab的结果相当：可以看出fc@1000Hz有-3dB的衰减。

73.1阶ButterworthHPF设计0,)1(,10,,)1(1)(11,)1()1(1)(11,11)(2110201011111111111ACGAABBBGBzCGGzGzHCGsetzCCzzHzzCsssH例3：设定fs=44100Hz,fc=1000Hz计算1阶ButterworthHPFfiltercoefficientsC1=tan(2*pi*1000/44100/2)=0.071358680867G=0.93339421975带入上式计算得FilterCoefficients：B=[0.933394219750-0.9333942197500]A=[1-0.8667884395000]与Matlab计算结果相当：频响如下

84.2阶ButterworthHPF设计scccffCCCGACGAAGBGBGBzCCGzCGGzGzGzHCCGsetzCCzCCCzzzHzzCssssH/2,2tan)14142136.1(),1(2,1,2,)14142136.1()1(212)(14142136.11)14142136.1()22()14142136.1(21)(11,4142136.111)(2221021022122122212221112例4：设定fs=44100Hz,fc=1000Hz计算2阶ButterworthHPFfiltercoefficientsC1=tan(2*pi*1000/44100/2)=0.071358680867G=0.904152203356带入上式计算得FilterCoefficients：B=[0.904152203356-1.8083044067120.904152203]A=[1-1.7990964097600.817510981662]与Matlab计算结果相当：频响如下

分享到：

赞收藏

资料库

Butterworth （巴特沃斯）滤波器设计参考.pdf

相关推荐

开发技术

热门标签

最新资料