logo资料库

数学实验图像畸变.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：1.32M 资料格式：doc 举报 版权申诉
第1页 / 共17页
第2页 / 共17页
第3页 / 共17页
第4页 / 共17页
第5页 / 共17页
第6页 / 共17页
第7页 / 共17页
第8页 / 共17页
资料共17页，剩余部分请下载后查看
    实验六 图像形状及颜色畸变的校正 一、 实验目的与要求 让学生了解数字图像的数学表达及相关概念，通过实验让学生加深对数学在 相关学科的应用价值的认识，培养学生的实际操作能力，并引导他们建立基础学 科在处理具体问题时方法上的联系。 二、 问题描述 对于在颜色或形状上发生畸变的图像，通过数学的方法实现校正。 三、问题分析 先由教师讲授数字图像的基本概念（包括图像的数学化、采样、量化、灰度、 各种数学图像的文件格式、表色系、颜色映像等），再通过具体的实例给学生示范 对于在颜色或形状上发生畸变的图像如何通过数学的方法实现校正的过程。最后 让学生动手完成对某些特殊畸变的图像的校正，写出数学原理和实验报告。 四、背景知识 1. 数字图像的数值描述及分类 图像是对客观存在物体的一种相似性的生动模仿与描述，是物体的一种不完 全的不精确的描述。数字图像是用一个数字阵列来表示的图像。数字阵列中的每 个数字，表示数字图像的一个最小单位，称为像素。采样是将空域上或时域上连 续的图像变换成离散采样点（像素）集合的一种操作。 对一幅图像采样后，若每行像素为 M 个，每列像素为 N 个，则图像大小为 MN 个像素。例如，一幅 640480 的图像，就表示这幅连续图像在长、宽方向上分别 分成 640 个和 480 个像素。显然，想要得到更加清晰的图像质量，就要提高图像 的采样像素点数，即使用更多的像素点来表示该图像。 客观世界是三维的，从客观场景中所拍摄到的图像是二维信息。因此，一幅 图像可以定义为一个二元函数 f(x,y),其中 x,y 是空间坐标。对任何一对空间坐标 (x,y)上的幅值 f(x,y)，成为表示图像在该点上的强度或灰度，或简称为像素值。因 为矩阵是二维结构的数据，同时量化值取整数，因此，一幅数字图像可以用一个 整数矩阵来表示。矩阵的元素位置(i,j)，就对应于数字图像上的一个像素点的位置。 矩阵元素的值 f(i,j)就是对应像素点上的像素值。 值得注意的是矩阵中元素 f(i,j)的坐标含义是 i 为行坐标，j 是列坐标。而像素 f(x,y )的坐标含义一般指直角坐标系中的坐标，两者的差异如下图： 0 列坐标(j) 纵坐标(y) 矩阵元素 f (i,j) 行坐标(i) 像素 f(x,y) 0 横坐标(x) 图 1.1 矩阵坐标系与直角坐标系 对应于不同的场景内容，数字图像可以大致分为二值图像，灰度图像，彩色 图像三类。 1
    1）二值图像 它是指每个像素不是黑就是白，其灰度值没有中间过度的图像。二值图像对 画面的细节信息比较粗略，适合于文字信息图像的描述。它的矩阵取值非常简单， 即 f(i,j)=0(黑),或 f(i,j)=1(白)，除此之外没有其他的取值。当然，0 和 1 表示黑或 白都只是人定义的，可以人为地反过来定义。这种图像具有数据量小的优点。 2）灰度图像 它是指每个像素的信息由一个量化后的灰度级来描述的数字图像，灰度图像 中不包含彩色信息。标准灰度图像中每个像素的灰度由一个字节表示，灰度级数 位 256 级，每个像素可以是 0~255（从纯黑到纯白）之间的任何一个值。值越接 近 0 就越黑，越接近 255 就越白。 3）彩色图像 常用的图像彩色模式有 RGB 模式、CMYK 模式和 HIS 模式，一般情况下只 使用 RGB 模式。它是根据三基色成像原理来实现对自然界中的色彩描述的。这 一原理认为，自然界中的所有颜色都可以由红，绿，蓝（R,G,B）三基色组合而 成。如果三种基色的灰度分别用一个字节（8bit）表示，则三基色之间不同的灰 度组合可以形成不同的颜色。 2. 数字图像质量决定因素 数字图像的效果与以下几个评价参数有关： 1）图像分辨率 即采样所获得的图像总像素的多少。 2）采样密度 即在图像上单位长度所包含的采样点数。采样密度的倒数是 像素间距。 3）采样频率 即一秒钟采样的次数。它反映了采样点之间的间隔大小，采 样频率越高，丢失的信息越少，图像的质量越好。 4）扫描分辨率 表示一台扫描仪输入图像的细微程度，指每英寸扫描所得的 点，单位是 DPI（DotPerInch）。数字越大，表示被扫描的图像转化为数字 化图像越逼真，扫描仪质量也越好。 3. 彩色空间 1） 三基色原理 近代的三色学说研究认为,人眼的视网膜中存在着三种锥体细胞,它们包含不 同的色素,对光的吸收和反射特性不同,对于不同的光就有不同的颜色感觉.研究发 现,第一种锥体细胞专门感受红光,第二和第三种锥体细胞则分别感受绿光和蓝光. 它们三者共同作用,使人们产生了不同的颜色感觉. 这三种色光以不同比例混合, 几乎可以得到自然界中的一切色光,混合色域最大;而且这三种色光具有独立性,其 中一种原色不能由另外的原色光混合而成,由此,称红,绿,蓝为色光三原色. 为了统 一 认 识 ,1931 年 国 际 照 明 委 员 会 (CIE) 规 定 了 三 原 色 的 波 长 nmR0.700=λ,nmG1.546=λ,nmB8.435=λ。 2） 彩色的基本特征 色调(hue) 色调又称为色相,是当人眼看到一种或多种波长的光时所产生的 彩色感觉,它反映颜色的种类,是决定颜色的基本特性.色调用红,橙,黄,绿,青,蓝,靛, 紫等术语来刻画. 不透明物体的色调是指该物体在日光的照射下,所反射的各光谱 成分作用于人眼的综合效果;透明物体的色调则是透过该物体的光谱综合作用的 效果。 饱和度(saturation) 饱和度是指颜色的纯度,即色彩含有某种单色光的纯净 2
    程度,它可用来区别颜色的深浅程度.对于同一色调的彩色光,饱和度越深颜色越鲜 明或说越纯,例如鲜红色饱和度高,而粉红色的饱和度低.完全饱和的颜色是指没有 渗入白光所呈现的颜色,例如仅由单一波长组成的光谱色就是完全饱和的颜色。 亮度(brightness) 亮度是视觉系统对可见物体辐射或者发光多少的感知属 性.亮度是光作用于人眼时所引起的明亮程度的感觉,它与被观察物体的发光强度 有关.由于其强度的不同,看起来可能会亮一些或暗一些.对于同一物体,照射光越强, 反射光也越强,感觉越亮;对于不同的物体在相同照射情况下,反射越强者看起来越 亮。 通常把色调和饱和度通称为色度。亮度是用来表示某彩色光的明亮程度,而 色度则表示颜色的类别与深浅程度。 4．图像畸变 从数字图像处理的观点来考察畸变校正, 实际上是一个图像恢复的过程, 是 对一幅退化了的图像进行恢复。在图像处理中，图像质量的改善和校正技术，也 就是图像复原，当初是在处理从人造卫星发送回来的劣质图像的过程中发展、完 善的。目前，图像畸变校正的应用领域越来越广，几乎所有涉及应用扫描和成像 的领域都需要畸变校正。图像在生成和传送的过程中，很可能会产生畸变，如： 偏色、模糊、几何失真、几何倾斜等等。前几种失真主要是体现在显示器上，而 后一种失真则多与图像集角度有关。不正确的显影，打印、扫描，抓拍受反射光 线的影响等方式，都会使图像产生偏色现像。模糊、几何畸变主要是在仪器采集 图片过程中产生，大多是因机器故障或操作不当影响导致，如在医学成像方面。 而几何空间失真广泛存在于各种实际工程应用中，尤其是在遥感、遥测等领域。 5．图像畸变校正过程所用到的重要工具 灰度直方图是关于灰度级分布的函数，是对图象中灰度级分布的统计。灰度 直方图是将数字图象中的所有像素，按照灰度值的大小，统计其所出现的频度。 通常，灰度直方图的横坐标表示灰度值，纵坐标为想像素个数。直方图上的一个 点的含义是，图像存在的等于某个灰度值的像素个数的多少。这样通过灰度直方 图就可以对图像的某些整体效果进行描述。从数学上讲，图像的灰度直方图是图 像各灰度值统计特征与图像灰度值出现的频率。从图形上来讲，它是一个一维曲 线，表征了图像的最基本的统计特征。 作为表征图像特征的信息而在图像处理中起着重要的作用。由于直方图反映了 图像的灰度分布状况，所以从对图像的观察与分析，到对图像处理结果的评价， 灰度直方图都可以说是最简单、最有效的工具。 五、实验过程 1．图像颜色畸变校正 图像颜色畸变校正在社会生活、工作中应用十分广泛。小到家庭生活图像处 理，大到医学成像应用、罪犯识别和国防侦察，都离不开它。图像颜色畸变现象 可以是由摄像器材导致，也可以是由于真实环境本身就偏色导致，还有的是由于 图像放置过久氧化、老化导致。无论其产生的原因如何，其校正方法都是类似的。 由于灰度图比较简单，因此本文跳过灰度图，直接研究彩色图的颜色畸变校 正，但无论是灰度图还是彩色图，其校正原理都是一样的，程序实现上只须对程 序进行小小的调整。 1） 图像颜色畸变校正算法 如果用 Matlab 显示颜色畸变的图像 RGB 基色直方图 ，发现相对正常图像， 3
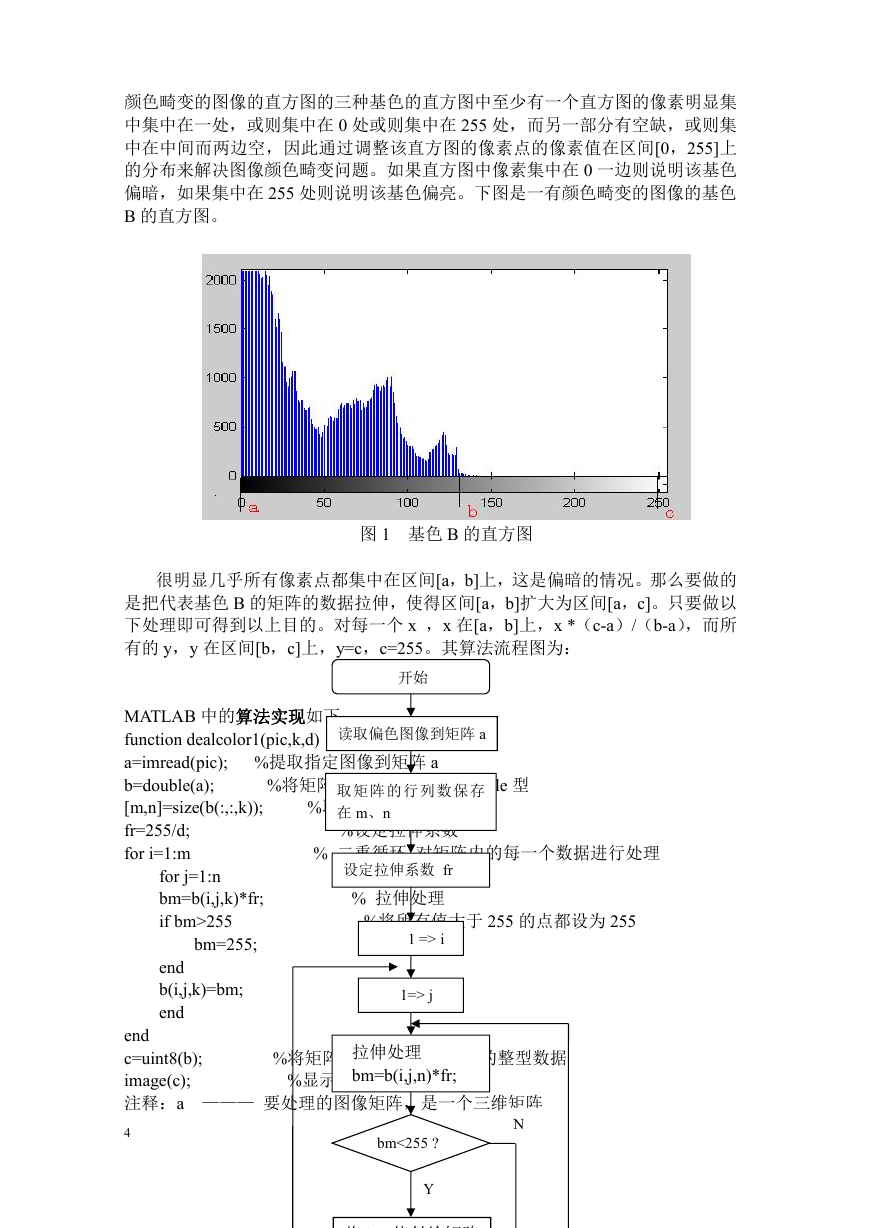
    颜色畸变的图像的直方图的三种基色的直方图中至少有一个直方图的像素明显集 中集中在一处，或则集中在 0 处或则集中在 255 处，而另一部分有空缺，或则集 中在中间而两边空，因此通过调整该直方图的像素点的像素值在区间[0，255]上 的分布来解决图像颜色畸变问题。如果直方图中像素集中在 0 一边则说明该基色 偏暗，如果集中在 255 处则说明该基色偏亮。下图是一有颜色畸变的图像的基色 B 的直方图。 图 1 基色 B 的直方图 很明显几乎所有像素点都集中在区间[a，b]上，这是偏暗的情况。那么要做的 是把代表基色 B 的矩阵的数据拉伸，使得区间[a，b]扩大为区间[a，c]。只要做以 下处理即可得到以上目的。对每一个 x ，x 在[a，b]上，x *（c-a）/（b-a），而所 有的 y，y 在区间[b，c]上，y=c，c=255。其算法流程图为： 开始 读取偏色图像到矩阵 a MATLAB 中的算法实现如下： function dealcolor1(pic,k,d) a=imread(pic); %提取指定图像到矩阵 a b=double(a); [m,n]=size(b(:,:,k)); fr=255/d; for i=1:m 取矩阵的行 列数保存 %取图像矩阵的行列数 在 m、n %设定拉伸系数 %将矩阵 a 的数据转化为 double 型 % 二重循环 对矩阵内的每一个数据进行处理 for j=1:n bm=b(i,j,k)*fr; if bm>255 bm=255; end b(i,j,k)=bm; end 设定拉伸系数 fr % 拉伸处理 1 => i 1=> j %将所有值大于 255 的点都设为 255 end c=uint8(b); image(c); 注释：a ——— 要处理的图像矩阵，是一个三维矩阵 4 拉伸处理 bm=b(i,j,n)*fr; %将矩阵 b 转化为 8 个字节的整型数据 %显示处理过的图像 N bm<255 ? Y 将 bm 值付给矩阵
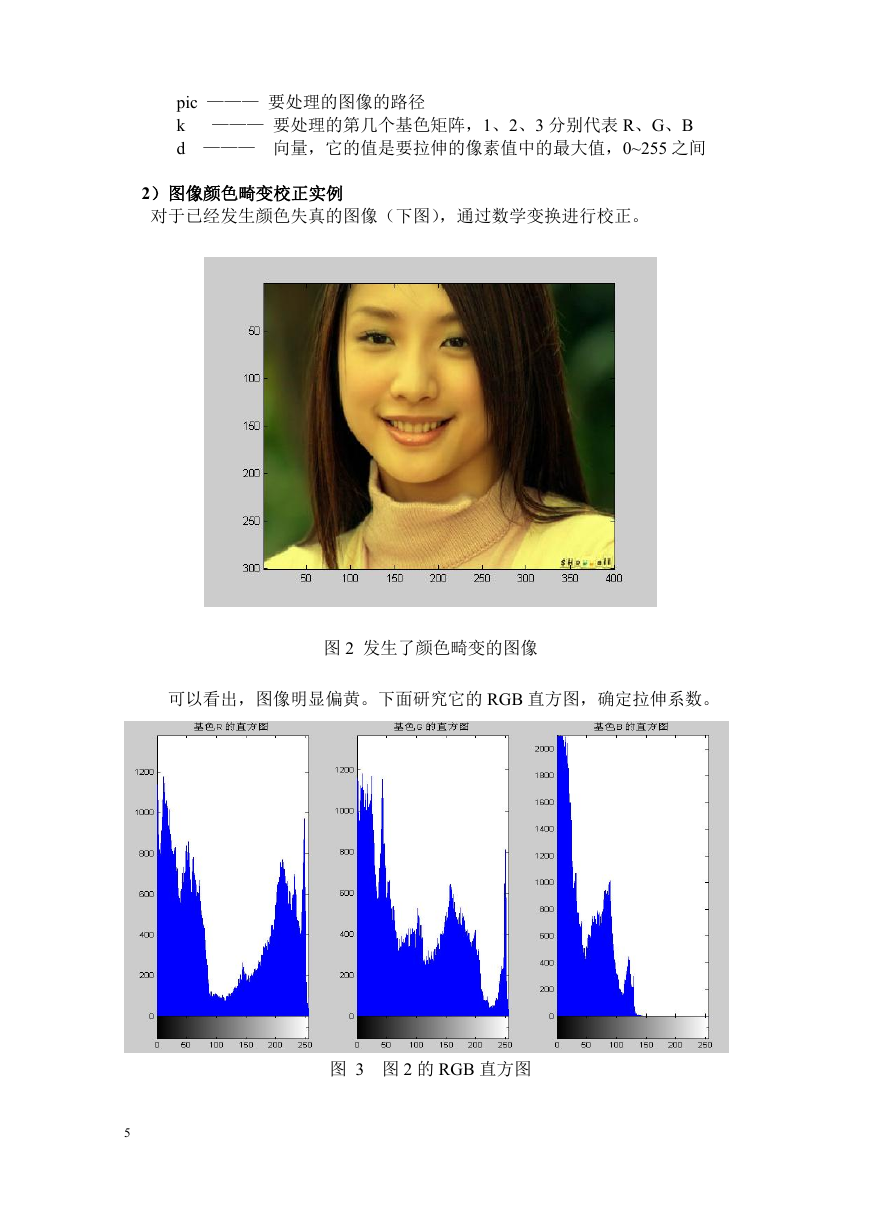
    pic ——— 要处理的图像的路径 k ——— 要处理的第几个基色矩阵，1、2、3 分别代表 R、G、B d ——— 向量，它的值是要拉伸的像素值中的最大值，0~255 之间 2）图像颜色畸变校正实例 对于已经发生颜色失真的图像（下图），通过数学变换进行校正。 图 2 发生了颜色畸变的图像 可以看出，图像明显偏黄。下面研究它的 RGB 直方图，确定拉伸系数。 图 3 图 2 的 RGB 直方图 5
    由于 R、G 的直方图则在 0 到 255 之间分布较为均匀，而在基色 B 的直方图 中，像素值的分布明显是集中在 140 以下的部分，而基本没有多少点在 140 到 255 之间，这说明基色 B 偏暗。像素值在 0~255 之间分布偏向一边是导致这幅图像颜 色畸变的原因，因此从基色 B 着手处理。 既然基色 B 直方图中像素分布不均匀，那么就应该把像素值在 0 到 140 之间 的点的像素值拉伸以至它们均匀分布在 0 到 255 上。因此做以下的处理。将代表 基色 B 的矩阵的每一个小于 140 的元素的值都乘以系数 255/140 ，显然这样可以 使区间[0，140] 拉伸为[0，255]，以达到需要的效果。因此处理函数的输入参数 为： dealcolor1(‘color.jpg’,3,140); 处理后得到的图片如下： 图 4 校正后的图像 很明显图像整体色质得到了很好的改善。 在这里参数 d 的值可以不断地变换，对比处理后的图像画质，选定一个最好 的值作为参数 d 的值来校正图像。经过测试，发现 d 的值在区间[130，160]得到 的校正图像基本没什么大的差别。 3）图像颜色畸变校正算法二 以上讨论的是单通道（单个基色直方图）向上调整（向 255 拉伸）的情况， 而双通道、三通道需要调整的情况跟单通道的调整方法是一样的，我们只需要研 究各个直方图，拿出需要的参数值，多次调用函数 function dealcolor(pic,n,d) 即可。 而对于需要向两边调整和向下调整（向 0 拉伸）的情况则只须先将需要拉伸的区 间平移到 0 处，再进行向上调整。这些只需要对算法做一个小小的改动就可以实 现。 function dealcolor(pic,n,d) % d 是一个包含两个元素的向量, d(1)表示拉伸区间的下界 d(2)表示拉伸区间的上界 a=imread(pic); b=double(a); [m,n]=size(b(:,:,n)); fr=255/(d(2)-d(1)); 6
    for i=1:m % 二重循环 对矩阵内的每一个数据进行处理 %将所有处理前值小于 d(1)的点的处理后的值设置为 0 for j=1:n bb= b(i,j,n)-d(1); %将每个元素值减去 d(1)向 0 靠拢 if bb<0 bb=0; end bm=bb*fr; if bm>255 % 拉伸处理 %将所有处理后值大于 255 的点都设为 255 bm=255; end b(i,j,n)=bm; end end c=uint8(b); image(c); %将矩阵 b 转化为 8 个字节的整型数据 2. 图像模糊校正 图像模糊校正的应用与偏色校正的应用一样广泛而重要，在很多领域它们具 有同样的重要地位：如医学成像、罪犯识别、国防侦察等等。虽然图像模糊校正 最先是由处理间谍卫星图像而发展起来的，但是随着摄像设备特别是随着摄像监 控技术在社会管理中的广泛应用，警察可以轻易从监控设备得到的犯罪罪犯图像 资料。但由于技术上的缺陷，得到的图像资料通常都是模糊的，如果不进行相关 的处理很难得到罪犯的特征，追缉工作难度也会增加。 1） 图像模糊校正算法 图像的灰度变化情况可以表现为一曲线。当读入一个图像后，灰度变化就转 变成了矩阵数据的变化。反映数据变化的数学手段可以采用微分算子。从数学的 微分含义来看，“一阶微分”是描述“数据的变化率”，“二阶微分”是描述“数据 变化率的变化率”。在感应灰度变化方面，二阶微分比一阶微分更具敏感性，尤其 是对斜坡渐变的细节。因此采用二阶微分算子来处理图像模糊校正。 最简单的各向同性微分算子是拉普拉斯微分算子。设原图为 f(x,y)，一个二维 的拉普拉斯微分算子定义为： 2  f  f 2 2  x   f 2 2  y  将它展开就得到 2  f  ,(4 yxf )  ( xf  ,1 y )  ( xf  ,1 y )  ,( yxf )1  ,( yxf  )1 。写成图像处理运 算模版的形式就是 L  算法的流程为： 0 1  0      1  4 1  0   1    0  。 7
    开始 读入图像到矩阵 a 取矩阵的长宽存放到 h,w 中 生成一个与矩阵 a 相同维数的矩阵 g 1=>Y 1=>X 1=>J 调用函数 pick_tem(),接收 返回值为相应输出图像点 J+1=>J 的像素值 X+1=>X Y JY 显示处理过的图像 g 结束 设处理后的图像为 g(x,y) ，则 ,( yxg )  ,( yxf ) 2  ,( yxf ) 。用模板表示则是 0L  0 1  0      1  5 1  0   1    0  ，模板中心点就是要处理的像素点。如果连对角线方向都考虑 的话，模板的形式就表现为 1L          1 1 1 1  9 1     1   1   1  。 由于模板是一个 3 阶矩阵，所以模板处理不了图像矩阵边缘的点。将这些处 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料