第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
ADI(交替方向隐格式)求解二维抛物方程(含matlab程序).docx
ADI法求解二维抛物方程
ADI 法求解二维抛物方程
学校：中国石油大学（华东） 学院：理学院 姓名：张道德 时间：2013.4.27
1、ADI 法介绍
作为模型，考虑二维热传导方程的边值问题：
,0
,
u
x y
yy
( ,
)
x y
( ,
, )
u l y t
u
u
t
xx
,0)
( ,
u x y
(0,
, )
u
y t
（3.6.1）
,
l t
0
( ,0, )
u x
t
( , , ) 0
u x l t
取 空 间 步 长 1
h
， 时 间 步 长 0t> ， 作 两 族 平 行 于 坐 标 轴 的 网 线 ：
M=
y
k
x
x
j
,
jh y
,
kh j k
,
将区域 0
0,1,
M
,
,
,x y
分割成 2M 个小矩形。第
l
一个 ADI 算法（交替方向隐格式）是 Peaceman 和 Rachford（1955）提出的。
方法：
由第 n 层到第 n+1 层计算分为两步：
（1）第一步：
式为：
从n->n+ ，求u 对 向后差分,u 向前差分 ，构造出差分格
yy
1
2
1
n
2
,
j k
u
xx
(3.6.1)
1
n
,
j k
u
1
n
-
2
u
,
j k
2
1
2
1,
n
j
k
u
2
=
（
1
n
2
u
,
j k
2
h
1
2
1,
n
j
k
u
u
n
,
j k
1
2
+
n
,
j k
2
u
h
u
n
,
j k
1
）
1 (
2
u
x
h
2
1
n
2
,
j k
2
u
y
n
,
j k
)
（2）第二步：
式为：
1
2
从n+ ->n+1，求u 对 向前差分,u 向后差分 ，构造出差分格
yy
1
n
2
,
j k
u
xx
(3.6.1)
2
n
,
j k
u
1
n
-
u
,
j k
2
1
2
1,
n
j
k
u
2
=
（
1
2
n
u
,
j k
2
h
1
2
1,
k
n
j
u
u
1
n
1
,
j k
2
+
1
n
,
j k
2
u
h
u
1
n
,
1
j k
）
1 (
2
x
h
2
1
n
2
,
j k
u
2
y
u
1
n
,
j k
)
其中
,
j k
1,
,
M
1,
n
0,1,2,
上表
,
n
1
2
表示在t=t
n
n
j ku 已 求 得 ， 则 由
假 定 第 n 层 的 ,
(3.6.1) 求 出
1
j ku
n
,
(
n
1
2
)
取值 。
， 这 只 需 按 行
1
2
1
2
(
j
1,
M
,
1)
解一些具有三对角系数矩阵的方程组；再由
(3.6.1) 求出
2
1
n
j ku ，这只需按列 (
,
k
1,
M
,
1)
解一些具有三对角系数矩阵的方程组，
所以计算时容易实现的。
2、数值例子
（1）问题
用 ADI 法求解二维抛物方程的初边值问题：
1 (
u
u
yy
xx
2
4
t
(0,
, )
, ) 0,0
(1,
y t
u
y t
u
( ,0, )
( ,1, ) 0,0
u x
t
u x
y
y
( ,
,0)
sin
.
u x y
y
1,
t
y
1,
x
t
cos
x y G
0,
0
(0,1)
),( ,
t
u
x
)
(0,1),
t
0,
已知（精确解为：
( ,
, )
u x y t
sin
y
cos
x
exp(
2
t
8
)
）
设
x
j
(
jh j
0,1,
,
J
),
y
k
(
kh k
0,1,
,
),
K t
n
(
n n
0,1,
n
j ku ，
差分解为 ,
N
)
,
n
u
则边值条件为： 0,
n
u
,0
j
k
u
u
n
,
J k
n
,
,1
j
0,
n
u
,
j K
k
1
0,1,
n
u
,
j K
,
j
,
K
0,1,
,
J
初值条件为： 0
u
,
j k
sin
x
cos
y
k
j
取空间步长
h
h
1
h
2
1 40
，时间步长 1 1600
网比
r
h
2
。用 ADI 法分
1
别计算到时间层 1t 。
（2）计算过程
从n到n+1时，
n
u
根据边值条件： 0,
k
u
n
,
J k
0,
k
，已经知道第 0 列和第 K 列数值全为 0。
0,1,
K
,
（1）
从n->n+ ，求u 对 向后差分,u 向前差分 ，构造出差分格式为：
yy
1
2
1
n
2
,
j k
u
xx
n
,
j k
u
1
n
-
2
u
,
j k
2
从而得到：
1
2
1,
n
j
k
u
1=
（
16
1 (
2
u
x
16
h
2
u
n
,
j k
1
2
+
n
,
j k
2
u
h
u
n
,
j k
1
）
1
2
1,
n
j
k
u
2
1
n
2
u
,
j k
2
h
1
n
2
,
j k
2
u
y
n
,
j k
)
1
2
1,
n
j
k
r
u
1
32
(1
1
16
1
n
2
,
j k
r
)
u
1
2
1,
n
j
k
r
u
1
32
1
32
r
u
n
,
j k
1
(1
1
16
r
)
u
n
,
j k
1
32
r
u
n
,
j k
1
， 其 中
j
1,2,
,
J
1,
k
1,2,
,
K
1
r
r
r
r
1
1
16
1
r
32
1
32
1
16
1
32
1
16
1
r
32
即按行用追赶法求解一系列下面的三对角方程组：
1
1
16
1
r
32
1
32
1
32
1
1
1
1
r
r
r
r
r
r
n
又根据边值条件得： ,0
j
u
u
n
,1
j
,
u
n
,
j K
1
n
j Ku
K 行 ,
,(
j
。
0,1,
J
)
,
n
,
j K
,
j
3
2
1
2
u
u
n
3,
k
n
u
1,
k
f
1
f
f
1
n
2
2,
k
1
2
1
32
1
16
0,1,
，解出第 0 行 ,0
1
2
3,
1
2
2,
1
2
1,
1) (
f
f
f
J
1) 1
,
r
r
n
J
n
J
n
J
u
u
u
1
1)
3
2
(
J
(
J
k
J
J
k
k
J
J
(
J
1) 1
n
ju 和第
1
32
1
16
1
r
32
u
从n+ ->n+1，求u 对 向前差分,u 向后差分 ，构造出差分格
yy
1
n
2
,
j k
u
xx
（2）第二步：
式为：
1
2
n
,
j k
u
1
n
-
u
,
j k
2
1
2
1,
k
n
j
u
1=
（
16
1 (
2
u
x
16
h
2
u
1
n
1
,
j k
2
+
1
n
,
j k
2
u
h
u
1
n
1
,
j k
）
1
2
1,
k
n
j
u
2
1
2
n
u
,
j k
2
h
1
n
2
,
j k
2
u
y
1
n
,
j k
)
r
)
u
1
n
,
j k
1
32
r
u
1
n
1
,
j k
1
n
2
1,
j
k
r
u
1
32
(1
1
16
1
2
n
,
j k
r
)
u
1
n
2
1,
j
k
r
u
1
32
， 其 中
1
16
从而得到：
1
32
r
u
1
n
1
,
j k
(1
j
1,2,
,
J
1,
k
1,2,
,
K
1
n
又根据边值条件得： ,0
j
u
u
n
,1
j
,
u
n
,
j K
1
u
n
,
j K
,
j
从而得到：
，
0,1,
J
,
u
n
,0
j
n
u
,
j K
u
1
n
,1
j
0
n
u
,
j K
0
其中 (
j
0,1,
,
J
)
即按列用追赶法求解一系列下面的三对角方程组：
r
1
32
1
16
1
r
1
32
1
32
r
r
1
r
1
16
1
r
32
K K
u
u
u
u
u
u
u
u
n
j
n
j
n
j
n
j
1
,0
1
,1
1
,2
1
,3
1
n
,
j K
1
n
,
j K
1
n
,
j K
1
n
,
j K
3
2
1
K
1
2
f
1
f
f
f
4
3
f
f
f
f
K
3
K
2
K
1
K
K
1
1
r
1
32
1
16
1
r
32
r
r
1
32
1
16
1
1
r
r
1
32
1
r
1
32
1
16
1
r
32
r
r
r
1
1
1
1
32
1
1
16
1
r
32
（3）求解结果
(3.1)数值解
y
1/4
x1/4
0.142057658092578
2/4
0.200899866713484
3/4
0.142057658092578
2/4
3/4
2.16292994886484e-15 3.03768181457584e-15 2.12330312762773e-15
-0.142057658092571
-0.142057658092570
-0.200899866713473
（3.2）精确解
y
1/4
x1/4
0.145606466607010
2/4
0.205918639844859
3/4
0.145606466607010
2/4
3/4
1.26088801585392e-17 1.78316493265431e-17 1.26088801585392e-17
-0.145606466607010
-0.145606466607010
-0.205918639844859
（3.3）数值解-精确解（即误差）
y
1/4
x1/4
-0.00354880851443196 -0.00501877313137564 -0.00354880851443273
2/4
3/4
2/4
3/4
2.15032106870631e-15 3.01985016524929e-15 2.11069424746919e-15
0.00354880851443973
0.00354880851444026
0.00501877313138652
从而得到误差的范数为：
1- 范数：0.233770443573713； 2-范数：0.196807761631447；
∞-范数：0.327253314506086
（3.4）图像
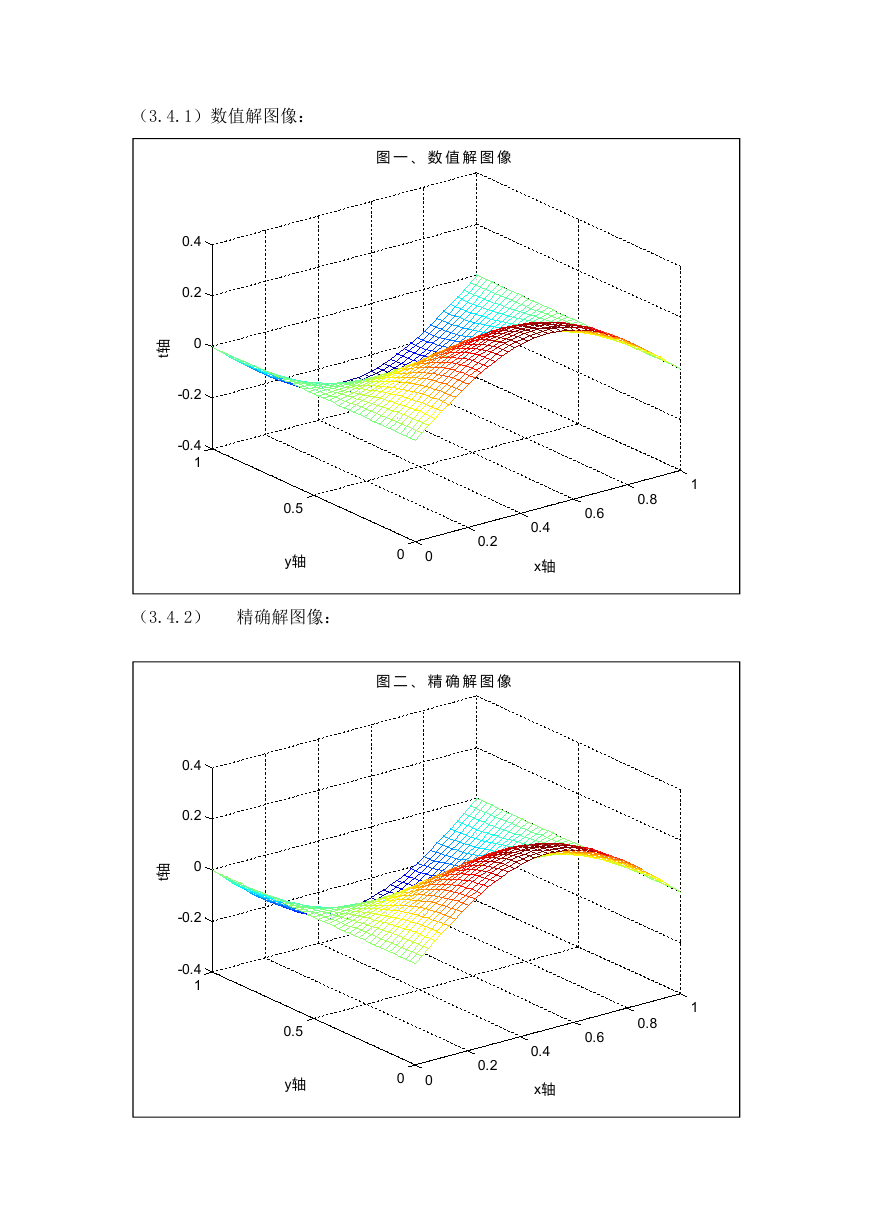
（3.4.1）数值解图像：
图 一 、 数 值 解 图 像
0.4
0.2
轴
t
0
-0.2
-0.4
1
0.5
y轴
0.2
0
0
0.4
x轴
1
0.8
0.6
（3.4.2） 精确解图像：
图 二 、 精 确 解 图 像
0.4
0.2
轴
t
0
-0.2
-0.4
1
0.5
y轴
0.2
0
0
0.4
x轴
1
0.8
0.6
%x取值范围
%y取值范围
（5）主要程序
（5.1）主程序
%*************************************************************
%main_chapter主函数
%信息10-2——张道德
%学号：10071223
clc
clear
a = 0; b=1;
c=0; d=1;
tfinal = 1;
t=1/1600;%时间步长；
h=1/40;%空间步长
r=t/h^2;%网比
x=a:h:b;
y=c:h:d;
%**************************************************************
%精确解
m=40;
u1=zeros(m+1,m+1);
for i=1:m+1,
%最终时刻
for j=1:m+1
u1(j,i) = uexact(x(i),y(j),1);
end
end
%数值解
u=ADI(a,b,c,d,t,h,tfinal);
%*****************************************************************
%绘制图像
figure(1) ;mesh(x,y,u1)
figure(2); mesh(x,y,u)
%误差分析
error=u-u1;
norm1=norm(error,1);
norm2=norm(error,2);
norm00=norm(error,inf);
%*****************************************************************
（5.2）ADI 函数
%****************************************************************
% 用ADI法求解二维抛物方程的初边值问题
%
%
%****************************************************************
精确解: u(t,x,y) = sin(pi*x) sin(pi*y)exp(-pi*pi*t/8)
u_t = 1/16（u_{xx} + u_{yy}）（0,1）*（0,1）
function [u]=ADI(a,b,c,d,t,h,tfinal )
%(a , b) x取值范围
%(c, d)
y取值范围
%tfinal最终时刻
%t时间步长；
%h空间步长
r=t/h^2;%网比
m=(b-a)/h;%
n=tfinal/t; %
x=a:h:b;
y=c:h:d;
%******************************************************************
%初始条件;使用了精确解函数？
u=zeros(m+1,m+1);
for i=1:m+1,
for j=1:m+1
u(j,i) = uexact(x(i),y(j),0);
end
end
%******************************************************************
u2=zeros(m+1,m+1);
a=-1/32*r*ones(1,m-2);
b=(1+r/16)*ones(1,m-1);
aa=-1/32*r*ones(1,m);
cc=aa;aa(m)=-1;cc(1)=-1;
bb=(1+r/16)*ones(1,m+1);
bb(1)=1;bb(m+1)=1;
for i=1:n
%**************************************************************
%从n->n+1/2,u_{xx}向后差分，u_{yy}向前差分
for j=2:m
for k=2:m
d(k-1)=1/32*r*(u(j,k+1)-2*u(j,k)+u(j,k-1))+u(j,k);
end
% 修正第一项与最后一项,但由于第一项与最后一项均为零，可以省略
%d(1)=d(1)+u1(j,1);d(m-1)=d(m-1)+u1(j,m+1);
u2(j,2:m)=zhuiganfa(a,b,a,d);
end
u2(1,:)=u2(2,:);
u2(m+1,:)=u2(m,:);
%**************************************************************
%从n->n+1,u_{xx}向前差分，u_{yy}向后差分
for k=2:m
dd(1)=0;dd(m+1)=0;
for j=2:m
dd(j)=1/32*r*(u2(j+1,k)-2*u2(j,k)+u2(j-1,k))+u2(j,k);
end
u(:,k)=zhuiganfa(aa,bb,cc,dd);
end
%****************************************************************
u2=u;
end
%********************************************************************
（5.3）“追赶法”程序
%********************************************************************
%追赶法
function [x]=zhuiganfa(a,b,c,d)
%对角线下方的元素，个数比A少一个
% %对角线元素
%对角线上方的元素，个数比A少一个
%d为方程常数项
%用追赶法解三对角矩阵方程
r=size(a);
m=r(2);
r=size(b);
n=r(2);
if size(a)~=size(c)|m~=n-1|size(b)~=size(d)
error('变量不匹配,检查变量输入情况!');
end
%%
%LU分解
u(1)=b(1);
for i=2:n
l(i-1)=a(i-1)/u(i-1);
u(i)=b(i)-l(i-1)*c(i-1);
v(i-1)=(b(i)-u(i))/l(i-1);
end
%追赶法实现
%%
%求解Ly=d，"追"的过程
y(1)=d(1);
for i=2:n
y(i)=d(i)-l(i-1)*y(i-1);
end
%%
%求解Ux=y,"赶"的过程
x(n)=y(n)/u(n);
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
