第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
Face Recognition using eigenfaces.pdf
c
Face Recognition Using Eigenfaces
Matthew A. Turk and Alex P. Pentland
Vision and Modeling Group, The Media Laboratory
Massachusetts Institute of Technology
Abstract
We present an approach t o the detection and
identification of human faces and describe a work-
ing, near-real-time face recognition system which
tracks a subject’s head and then recognizes the per-
son by comparing characteristics of the face to those
of known individuals. Our approach treats face
recognition as a two-dimensional recognition prob-
lem, taking advantage of the fact that faces are are
normally upright and thus may be described by a
small set of 2-D characteristic views. Face images
are projected onto a feature space (“face space”)
that best encodes the variation among known face
images. The face space is defined by the “eigen-
faces”, which are the eigenvectors of the set of faces;
they do not necessarily correspond to isolated fea-
tures such as eyes, ears, and noses. The framework
provides the ability to learn t o recognize new faces
in an unsupervised manner.
1
Introduction
Developing a computational model of face recogni-
tion is quite difficult, because faces are complex,
multidimensional, and meaningful visual stimuli.
They are a natural class of objects, and stand in
stark contrast to sine wave gratings, the “blocks
world”, and other artificial stimuli used in human
and computer vision research[l]. Thus unlike most
early visual functions, for which we may construct
detailed models of retinal or striate activity, face
recognition is a very high level task for which com-
putational approaches can currently only suggest
broad constraints on the corresponding neural ac-
tivity.
We therefore focused our research towards devel-
oping a sort of early, preattentive pattern recogni-
tion capability that does not depend upon having
full three-dimensional models or detailed geometry.
Our aim was to develop a computational model of
face recognition which is fast, reasonably simple,
and accurate in constrained environments such as
an office or a household.
Although face recognition is a high level visual
problem, there is quite a bit of structure imposed on
the task. We take advantage of some of this struc-
ture by proposing a scheme for recognition which is
based on an information theory approach, seeking
to encode the most relevant information in a group
of faces which will best distinguish them from one
CH2983-5/91/0000/0586/$01 .OO (0 1991 IEEE
586
another. T h e approach transforms face images into
a small set of characteristic feature images, called
eigenfaces” , which are the principal components of
“ ’
the initial training set of face images. Recognition is
performed by projecting a new image into the snb-
space spanned by the eigenfaces (“face space”) and
then classifying the face by comparing its position in
face space with the positions of known individuals.
Automatically learning and later recognizing new
faces is practical within this framework. Recogni-
tion under reasonably varying conditions is achieved
by training on a limited number of characteristic
views (e.g., a “straight on” view, a 45’ view, and
a profile view). The approach has advantages over
other face recognition schemes in its speed and sim-
plicity, learning capacity, and relative insensitivity
to small or gradual changes in the face image.
1.1 Background and related work
Much of the work in computer recognition of faces
has focused on detecting individual features such as
the eyes, nose, mouth, and head outline, and defin-
ing a face model by the position, size, and relation-
ships among these features. Beginning with Bled-
soe’s [2] and Kanade’s [3] early systems, a number
of automated or semi-automated face recognition
strategies have modeled and classified faces based
on normalized distances and ratios among feature
points. Recently this general approach has been
continued and improved by the recent work of Yuille
et al. [4].
Such approaches have proven difficult to extend
to multiple views, and have often been quite frag-
ile. Research in human strategies of face recogni-
tion, moreover, has shown that individual features
and their immediate relationships comprise an insuf-
ficient representation to account for the performance
of adult human face identification [ 5 ] . Nonetheless,
this approach to face recognition remains the most
popular one in the computer vision literature.
Connectionist approaches to face identification
sepk to capture the configurational, or gestalt-like
nature of the task. Fleming and Cottrell [6], build-
ing on earlier work by Kohonen and Lahtio [7], use
nonlinear units to train a network via back propa-
gation to classify face images. Stonham’s WISARD
system [8] has been applied with some success to bi-
nary face images, recognizing both identity and ex-
pression. Most connectionist systems dealing with
faces trrat thr input image as a general 2-D pattern,
and can make no explicit use of the configurational
properties of a face. Only very simple systems have
been explored to date, and it is unclear how they
will scale to larger problems.
Recent work by Burt et al. uses a “smart sensing”
approach based on multiresolution template match-
ing [9]. This coarse-to-fine strategy uses a special-
purpose computer built to calculate multiresolution
pyramid images quickly, and has been demonstrated
identifying people in near-real-time. The face mod-
els are built by hand from face images.
2 Eigenfaces for Recognition
Much of the previous work on automated face recog-
nition has ignored the issue of just what aspects of
the face stimulus are important for identification,
assuming that predefined measurements were rele-
vant and sufficient. This suggested to us that an
information theory approach of coding and decod-
ing face images may give insight into the information
content of face images, emphasizing the significant
local and global “features”. Such features may or
may not be directly related to our intuitive notion
of face features such as the eyes, nose, lips, and hair.
In the language of information theory, we want
to extract the relevant information in a face image,
encode it as efficiently as possible, and compare one
face encoding with a database of models encoded
similarly. A simple approach to extracting the infor-
mation contained in an image of a face is to somehow
capture the variation in a collection of face images,
independent of any judgement of features, and use
this information t o encode and compare individual
face images.
In mathematical terms, we wish to find the prin-
cipal components of the distribution of faces, or the
eigenvectors of the covariance matrix of the set of
face images. These eigenvectors can be thought of
as a set of features which together characterize the
variation between face images. Each image location
contributes more or less to each eigenvector, so that
we can display the eigenvector as a sort of ghostly
face which we call an eigenface. Some of these faces
are shown in Figure 2.
Each face image in the training set can be repre-
sented exactly in terms of a linear combination of
the eigenfaces. The number of possible eigenfaces is
equal to the number of face images in the training
set. However the faces can also be approximated us-
ing only the “best” eigenfaces - those that have the
largest eigenvalues, and which therefore account for
the most variance within the set of face images. The
primary reason for using fewer eigenfaces is compu-
tational efficiency. The best M’ eigenfaces span an
of all
M’-dimensional subspace
possible images. As sinusoids of varying frequency
and phase are the basis functions of a fourier de=
composition (and are in fact eigenfunctions of linear
systems), the eigenfaces are the basis vectors of the
eigenface decomposition.
“face space”
~
~
The idea of using eigenfaces was motivated by a
technique developed by Sirovich and Kirby [lo] for
efficiently representing pictures of faces using prin-
cipal component analysis. They argued that a col-
lection of face images can be approximately recon-
structed by storing a small collection of weights for
each face and a small set of standard pictures.
It occurred to us that if a multitude of face im-
ages can be reconstructed by weighted sums of a
small collection of characteristic images, then an ef-
ficient way to learn and recognize faces might be
to build the characteristic features from known face
images and to recognize particular faces by compar-
ing the feature weights needed to (approximately)
reconstruct them with the weights associated with
the known individuals.
The following steps summarize the recognition
process:
1. Initialization: Acquire the training set of face
images and calculate the eigenfaces, which de-
fine the face space.
2. When a new face image is encountered, calcu-
late a set of weights based on the input image
and the M eigenfaces by projecting the input
image onto each of the eigenfaces.
3. Determine if the image is a face at all (whether
known or unknown) by checking to see if the
image is sufficiently close to “face space.”
4. If it is a face, classify the weight pattern as
either a known person or as unknown.
5. (Optional) If the same unknown face is seen
several times, calculate its characteristic weight
pattern and incorporate into the known faces
(i.e., learn to recognize it).
2.1 Calculating Eigenfaces
Let a face image 1(z, y) be a two-dimensional N by
N array of intensity values, or a vector of dimension
N 2 . A typical image of size 256 by 256 describes a
vector of dimension 65,536, or, equivalently, a point
in 65,536-dimensional space. An ensemble of im-
ages, then, maps to a collection of points in this
huge space.
Images of faces, being similar in overall configura-
tion, will not be randomly distributed in this huge
image space and thus can be described by a rel-
atively low dimensional subspace. The main idea
of the principal component analysis (or Karhunen-
Loeve expansion) is to find the vectors which best
account for the distribution of face images within
the entire image space. These vectors define the
subspace of face images, which we call “face space”.
Each vector is of length N 2 , describes an N by N
image, and is a linear combination of the original
face images. Because these vectors are the eigen-
vectors of the covariance matrix corresponding to
the original face images, and because they are face-
like in appearance, we refer to them as “eigenfaces.”
Some examples of eigenfaces are shown in Figure 2.
( b )
Figure 1: ( a ) Face images used as the training
w t . ( b ) The average face q.
Let
the
face
training
images he
set of
filled by Q’ = + c;l’=,
1 I. r2. r3. ... r.,~. The average face of the set is de-
r,. Each face differs from
the average by the vector @i = r, - 9. An example
training set is shown in Figure l ( a ) , with the average
face q shown in Figure l ( b ) . This set of very large
vectors is then subject t o principal component anal-
ysis. which seeks a set of ,If orthonormal vectors u n
and their associated eigenvalues Xk which best de-
scribes the distribution of the data. The vectors uk
and scalars X k are the eigenvectors and eigenvalues.
respectively. of the covariance matrix
i l i
= AA’
where the matrix A = [ @ I @2 ... @.v 1. The matrix
C’. however, is AVz by *Y2, and determining the .ITz
eigenvectors and eigenvalues is an intract able task
for typical image sizes. We need a computationally
feasible method to find these eigenvectors. Fortu-
nately we can determine the eigenvectors by first
solving a much smaller M by hf matrix problem.
and taking linear combinations of the resulting vec-
tors. (See [ll] for the details.)
U-ith this analysis the calculations are greatly re-
duced. from the order of the number of pixels in the
images ( S 2 ) to the order of the number of imagrs
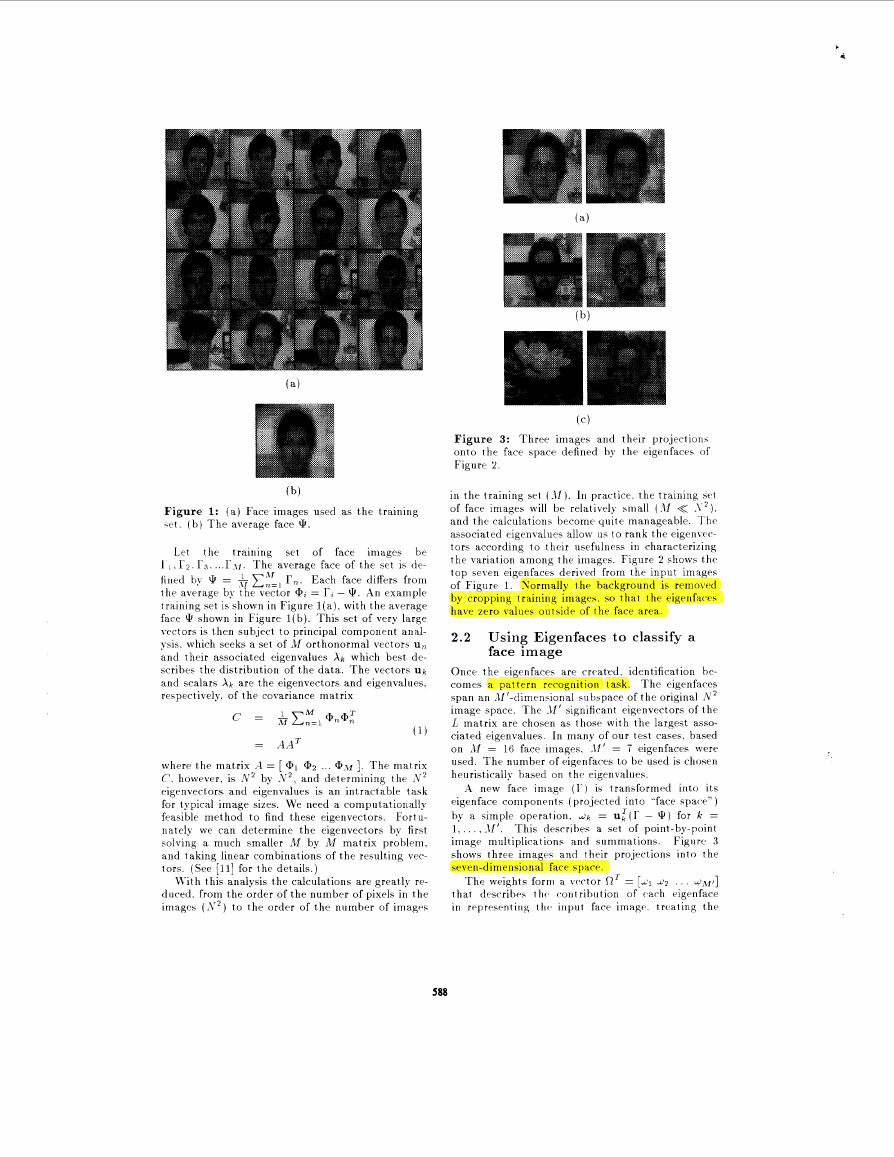
Figure 3: Three images and their projection\
onto the face space defined by the eigenfaces of
Figure 2
in the training set (-11). In practice. the training sct
of face images will tie relatively sinal1 (.U << .Yz).
and the calculation> tieconie quite manageable. Thcl
associated eigenvalues allow us to rank the eigei1vc.c-
tors according t o their usefulness in characterizing
the variation among the irnagrs. Figure 2 shows thr.
top seven eigenfaces derived from the input images
of Figure 1. Normally the background is removed
by cropping training imagcs. so that the eigenfares
have zero values outside of the face area.
2.2 Using Eigenfaces to classify a
face image
Once the eigenfaces are crr.at.ed. identification be-
comes a pattern recognition task. The eigenfaces
span an df’-dimensional subspace of the original N‘
image space. The -11’ significant eigenvectors of t he
L matrix are chosen as thosr. with the largest asso-
ciated eigenvalues. In many of our test cases. based
on Jf = 16 face images. .If’ = i eigenfaces were
used. The number of rigerifaces to be used is chosen
heuristically hased on t ht, eigenvalues.
A nrw face imagr ( I ’ ) is transformrd into its
pigenface coniponrnts (projected into ”face space” )
by a simple operation. d k = u:(r - 9 ) for k =
1. . . . . -11’. This drscribrs a set of point-by-point
image multiplications and summations. Fignre 3
shows three imagrs and their projections into the
seren-dimensional facr. space.
The weights form a vcc‘tor R’ = [dl 4 . . . dnf,]
that dcwribr5 tht. coiitribution of cach eigenface
in reprrsrntiiig t h ( . input face imagr.. treating the
588
Figure 2: Seven of the eigenfaces calculated from the images of Figure 1, without the background removed.
eigenfaces as a basis set for face images. The vec-
tor is used to find which of a number of pre-defined
face classes, if any, best describes the face. The sim-
plest method for determining which face class pro-
vides the best description of an input face image is
to find the face class lc that minimizes the Euclid-
ian distance Ck = Il(0 - Ok)ll, where 0 k is a vector
describing the lcth face class. A face is classified as
belonging t o class lc when the minimum C k is be-
low some chosen threshold Be. Otherwise the face is
classified as “unknown”.
2.3 Using Eigenfaces to detect faces
We can also use knowledge of the face space to de-
tect and locate faces in single images. This allows
us to recognize the presence of faces apart from the
task of identifying them.
Creating the vector of weights for an image is
equivalent to projecting the image onto the low-
dimensional face space. The distance E between the
image and its projection onto the face space is sim-
ply the distance between the mean-adjusted input
image @ = r - Q and af = ~ i ? ; ” ‘ W k U k , its pro-
jection onto face space.
As seen in Figure 3, images of faces do not change
radically when projected into the face space, while
the projection of non-face images appear quite dif-
ferent. This basic idea is used to detect the presence
of faces in a scene: at every location in the image,
calculate the distance E between the local subimage
and face space. This distance from face space is used
as a measure of “faceness”, so the result of calculat-
ing the distance from face space at every point in
the image is a “face map” E ( z , Y ) . Figure 4 shows
an image and its face map - low values (the dark
area) indicate the presence of a face. There is a dis-
tinct minimum in the face map corresponding to the
location of the face in the image.
Unfortunately, direct calculation of this distance
measure is rather expensive. We have therefore de-
veloped a simpler, mote efficient method of calcu-
lating the face map e ( z , y ) , which is described in
[Ill.
2.4 Face space revisited
An image of a face, and in particular the faces in the
training set, should lie near the face space, which
in general describes images that are “face-like”. In
other words, the projection distance E should be
within some threshold 06. Images of known individ-
(a)
(b)
Figure 4: (a) Original image.
(b) Face map,
where low values (dark areas) indicate the pres-
ence of a face.
4
Figure 5: A simplified version of face space to
illustrate the four results of projecting an image
into face space. In this case, there are two eigen-
faces (u1 and U*) and three known individuals
(01, 0 2 , and 0 3 ) .
uals should project to near the corresponding face
class, i.e. Ck < 0,. Thus there are four possibilities
for an input image and its pattern vector: (1) near
face space and near a face class; (2) near face space
but not near a known face class; (3) distant from
face space and near a face class; and (4) distant from
face space and not near a known face class. Figure
5 shows these four options for the simple example
of two eigenfaces.
In the first case, an individual is recognized and
identified. In the second case, an unknown individ-
ual is present. The last two cases indicate that the
image is not a face image. Case three typically shows
up as a false positive in most recognition systems; in
our framework, however, the false recognition may
be detected because of the significant distance be-
tween the image and the subspace of expected face
589
images. Figure 3 shows some images and their pro-
jections into face space. Figure 3 (a) and (b) are
examples of case 1, while Figure 3 (c) illustrates
case 4.
In our current system calculation of the eigenfaces
is done offline as part of the training. The recogni-
tion currently takes about 350 msec running rather
inefficiently in Lisp on a Sun Sparcstation 1, using
face images of size 128x128.
3 Recognition Experiments
To assess the viability of this approach to face recog-
nition, we have performed experiments with stored
face images and built a system to locate and rec-
ognize faces in a dynamic environment. We first
created a large database of face images collected un-
der a wide range of imaging conditions. Using this
database we have conducted several experiments to
assess the performance under known variations of
lighting, scale, and orientation.
The images from Figure l ( a ) were taken from a
database of over 2500 face images digitized under
controlled conditions. Sixteen subjects were digi-
tized at all combinations of three head orientations,
three head sizes or scales, and three lighting condi-
tions. A six level gaussian pyramid was constructed
for each image, resulting in image resolution from
512x512 pixels down to 16x16 pixels.
In the first experiment the effects of varying light-
ing. size, and head orientation were investigated us-
ing the complete database of 2500 images. Various
groups of sixteen images were selected and used as
the training set. Within each training set there was
one image of each person, all taken under the same
conditions of lighting, image size, and head orienta-
tion. All images in the database were then classified
as being one of these sixteen individuals - no faces
were rejected as unknown.
Statistics were collected measuring the mean ac-
curacy as a function of the difference between the
training conditions and the test conditions. In the
case of infinite 8, and 8 6 , the system achieved ap-
proximately 96% correct classification averaged over
lighting variation, 85% correct averaged over orien-
tation variation, and 64% correct averaged over size
variation.
In a second experiment the same procedures were
followed, but the acceptance threshold 8, was also
varied. At low values of O,, only images which
project very closely to the known face classes (cases
1 and 3 in Figure 5 ) will be recognized, so that there
will be few errors but many of the images will be
rejected as unknown. At high values of 8, most im-
ages will be classified, but there will be more errors.
Adjusting 8, t o achieve 100% accurate recognition
boosted the unknown rates to 19% while varying
lighting, 39% for orientation, and 60% for size. Set-
ting the unknown rate arbitrarily to 20% resulted
in correct recognition rates of loo%, 94%, and 74%
respectively.
c
Figure 6: The head tracking and locating sys-
tem.
These experiments show an increase of perfor-
mance accuracy as the acceptance threshold de-
creases. This can be tuned to achieve effectively
perfect recognition as the threshold tends to zero,
but at the cost of many images being rejected as
unknown. The tradeoff between rejection rate and
recognition accuracy will be different for each of the
various face recognition applications.
The results also indicate that changing lighting
conditions causes relatively few errors, while perfor-
mance drops dramatically with size change. This is
not surprising, since under lighting changes alone
the neighborhood pixel correlation remains high,
but under size changes the correlation from one im-
age to another is quite low. It is clear that there is
a need for a multiscale approach, so that faces a t a
particular size are compared with one another.
4 Real-time recognition
People are constantly moving. Even while sitting,
we fidget and adjust our body position, blink, look
around, and such. For the case of a moving person
in a static environment, we built a simple motion
detection and tracking system, depicted in Figure
6, which locates and tracks the position of the head.
Simple spatio-temporal filtering followed by a non-
linearity accentuates image locations that change in
intensity over time, so a moving person “lights up”
in the filtered image.
After thresholding the filtered idage to produce a
binary motion image, we analyze the “motion blobs”
over time to decide if the motion is caused by a per-
son moving and to determine head position. A few
simple rules are applied, such as “the head is the
small upper blob above a larger blob (the body)”,
and “head motion must be reasonably slow and con-
tiguous” (heads aren’t expected to j u m p around the
image erratically). Figure 7 shows an image with
the head located, along with the path of the head in
the preceding sequence of frames.
We have used the techniques described above to
build a system which locates and recognizes faces
in near-real-time in a reasonably unstructured envi-
ronment. When the motion detection and analysis
590
The eigenface approach to face recognition was
motivated by information theory, leading to the idea
of basing face recognition on a small set of image fea-
tures that best approximate the set of known face
images, without requiring that they correspond to
our intuitive notions of facial parts and features. Al-
though it is not an elegant solution to the general
object recognition problem, the eigenface approach
does provide a practical solution that is well fitted
to the problem of face recognition. It is fast, rela-
tively simple, and has been shown to work well in a
somewhat constrained environment.
References
Davies, Ellis, and Shepherd (eds.), Perceiving
and Remembering Faces, Academic Press, Lon-
don, 1981.
W. W. Bledsoe, “The model method in facial
recognition,” Panoramic Research Inc., Palo
Alto, CA, Rep. PRI:15, Aug. 1966.
T. Kanade, “Picture processing system by com-
puter complex and recognition of human faces,”
Dept. of Information Science, Kyoto University,
Nov. 1973.
A. L. Yuille, D. S. Cohen, and P. W. Halli-
nan, “Feature extraction from faces using de-
formable templates,” Proc. CVPR, San Diego,
CA, June 1989.
S. Carey and R. Diamond, “From piecemeal
to configurational representation of faces,” Sci-
ence, Vol. 195, Jan. 21, 1977, 312-13.
M. Fleming and G. Cottrell, “Categorization
of faces using unsupervised feature extraction,”
Proc. IJCNN-90, Vol. 2.
T. Kohonen and P. Lehtio, “Storage and pro-
cessing of information in distributed associa-
tive memory systems,” in G. E. Hinton and
J . A. Anderson, Parallel Models of Associative
Memory, Hillsdale, NJ: Lawrence Erlbaum As-
sociates, 1981, pp. 105-143.
T. 3. Stonham, “Practical face recognition and
verification with WISARD,” in H. Ellis, M.
Jeeves, F. Newcombe, and A. Young (eds.), As-
pects of Face Processing, Martinus Nijhoff Pub-
lishers, Dordrecht, 1986.
P. Burt, “Smart sensing within a Pyramid Vi-
sion Machine,” Proc. IEEE, Vol. 76, No. 8,
Aug. 1988.
L. Sirovich and M. Kirby, “Low-dimensional
procedure for the characterization of human
faces,” J . Opt. Soc. A m . A , Vol. 4, No. 3, March
1987, 519-524.
[ll] M. Turk and A. Pentland, “Eigenfaces for
Journal of Cognitive Neuro-
Recognition”,
science, March 1991.
591
Figure 7 : The head has been located - the im-
age in the box is sent to the face recognition pro-
cess. Also shown is the path of the head tracked
over several previous frames.
programs finds a head, a subimage, centered on the
head, is sent to the face recognition module. Using
the distance-from-face-space measure E , the image
is either rejected as not a face, recognized as one
of a group of familiar faces, or determined to be an
unknown face. Recognition occurs in this system at
rates of up to two or three times per second.
5 Further Issues and Conclusion
We are currently extending the system to deal with
a range of aspects (other than full frontal views)
by defining a small number of face classes for each
known person corresponding to characteristic views.
Because of the speed of the recognition, the system
has many chances within a few seconds to attempt
to recognize many slightly different views, at least
one of which is likely to fall close to one of the char-
acteristic views.
An intelligent system should also have an abil-
ity t o adapt over time. Reasoning about images
in face space provides a means to learn and sub-
sequently recognize new faces in an unsupervised
manner. When an image is sufficiently close to face
space (i.e., it is face-like) but is not classified as one
of the familiar faces, it is initially labeled as “un-
known”. The computer stores the pattern vector
and the corresponding unknown image.
If a col-
lection of “unknown” pattern vectors cluster in the
pattern space, the presence of a new but unidentified
face is postulated.
A noisy image or partially occluded face should
cause recognition performance t o degrade grace-
fully., since the system essentially implements an
autoassociative memory for the known faces (as de-
scribed in [7]). This is evidenced by the projection
of the occluded face image of Figure 3(b).
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
