图像混沌加密.pdf

发布时间：2022-06-18 发布人：admin 分类：说明书资料大小：2.26M 资料格式：pdf 举报版权申诉

3b959964-d1ac-4aa2-9396-493b69bbb557.pdf-第1页.png

第1页 / 共6页

3b959964-d1ac-4aa2-9396-493b69bbb557.pdf-第2页.png

第2页 / 共6页

3b959964-d1ac-4aa2-9396-493b69bbb557.pdf-第3页.png

第3页 / 共6页

3b959964-d1ac-4aa2-9396-493b69bbb557.pdf-第4页.png

第4页 / 共6页

3b959964-d1ac-4aa2-9396-493b69bbb557.pdf-第5页.png

第5页 / 共6页

3b959964-d1ac-4aa2-9396-493b69bbb557.pdf-第6页.png

第6页 / 共6页

文本预览

第 39 卷第 5 期 2018 年 3 月包装工程 PACKAGING ENGINEERING ·179· 一个切换 Lorenz 混沌系统在图像加密中的应用徐扬，黄迎久，李海荣（内蒙古科技大学，包头 014010）摘要：目的将一种新型的切换 Lorenz 混沌系统引入到图像加密系统中，以提高图像加密的效果。方法图像加密系统采取“置乱-扩散-置乱-扩散”的过程，首先结合密钥 K，将切换 Lorenz 混沌系统结合四阶龙格-库塔方程对明文图像进行离散，并通过 Arnold 映射对明文图像矩阵进行置乱；通过“异或”位运算对图像进行扩散处理；再通过 Logistic 映射对图像进行置乱；最后通过“循环移位”运算对图像进行扩散处理。结果经过仿真实验对图像加密性能进行测试，密文图像的相关指标参数 NPCR 和 UACI 的测试值分别约为 99.60 和 33.4，都很接近于它们的理论值，信息熵的测试结果约为 7.997，也非常接近于理论值 8。结论表明引入新型切换 Lorenz 混沌系统的图像加密系统具有较强的鲁棒性、可靠的安全性，可以有效地提高加密系统的各种抗攻击能力。关键词：切换 Lorenz 混沌系统；图像加密；Arnold 映射；Logistic 映射中图分类号：TS206 文献标识码：A 文章编号：1001-3563(2018)05-0179-06 DOI：10.19554/j.cnki.1001-3563.2018.05.034 Application of a Switched Lorenz Chaotic System in Image Encryption XU Yang, HUANG Ying-jiu, LI Hai-rong (Inner Mongolia University of Science & Technology, Baotou 014010, China) ABSTRACT: The work aims to introduce a new type of switched Lorenz chaotic system into image encryption system to improve the effect of image encryption. When the image encryption system adopted the "scrambling-diffusion- scrambling -diffusion” process, firstly, combined with the key K, the switched Lorenz chaotic system was combined with four order Runge-Kutta equations to discretize the plain image, and the plain image matrix was scrambled through the Arnold map- ping; the image was diffused through the bit "exclusive-OR" operation; and then the image was scrambled through the Logistic mapping; finally, the image was diffused through the "cyclic shift" operation. Through the simulation experiment to test the performance of image encryption, the test values of the encrypted image's related parameters NPCR and UACI were approximately 99.60 and 33.4, respectively, which were very close to the theoretical values. The information entropy test result was approximately 7.997, which was also very close to the theoretical value of 8. It is shown that the image encryption system with new switched Lorenz chaotic system has strong robustness and reliable security, and can effec- tively improve the anti-attack capability of the encryption system. KEY WORDS: switched Lorenz chaotic system; image encryption; Arnold mapping; Logistic mapping 近年来，随着互联网的飞速发展，大量图形和图像等多媒体信息通过网络进行传输，如何安全地输送这些信息成为一个迫切需要解决的问题。早在 1989 年，R. Matthews 首次使用 logistic 映射生成大量的伪随机数据用于加密[1]，之后，人们逐渐认识到混沌系统具有的初值敏感性、内随机性、遍历性等特点非常适用于图像加密算法，于是大量学者开始致力于研究混沌系统在图像加密算法中的应用。 2004 年，收稿日期：2017-06-12 基金项目：内蒙古自治区自然科学基金（2017MS0604）；内蒙古科技大学创新基金（2015XYPYL06）作者简介：徐扬（1980—），女，硕士，内蒙古科技大学讲师，主要研究方向为计算机图像和大数据。

·180· 包装工程 2018 年 3 月 G.R.Chen, Y.Mao, C.K.Chui 和 S.Lian 定义了 NPCR 和 UACI 这 2 个评价指标[2—3]，标志着混沌图像加密进入了蓬勃发展的阶段。2012—2015 年间，混沌图像加密进入了成熟期，在此期间，出现了许多新型的混沌图像加密算法，例如 Y.ZHANG 等提出了基于明文关联的混沌图像加密方法[4—7]。 Lorenz 系统作为最为经典的混沌系统之一，一直受到广泛的研究与应用，许多新的类 Lorenz 系统相继被提出并应用于图像加密算法中，如著名的 Chen 系统、Lü 系统等。同时大量的实验证明，单一的混沌系统加密算法存在密钥空间小等缺陷，其安全性不能满足实际应用的要求[8—9]。文中引入一个新型的切换 Lorenz 混沌系统[10]，再结合 Arnold 映射以及二维 Logistic 混沌映射，构成一个新型的图像加密系统，使图像加密系统具有更大的复杂性，克服单纯使用一种混沌系统的缺陷。 1 切换 Lorenz 混沌系统 f x ( ) (2) 新型的切换 Lorenz 混沌系统的数学模型为：  x     y     z  (1) x a y ) (   cy xz bx   hz xf x ( )  y x 0 ,     x x , 0   式中：a, b, c 为系统常量，a=20, b=14, c=10.6；h 为系统的控制参数。文献[10]中对式（1）的动力特性进行了详尽的分析，并给出了参数 h 与 Lyapunov 指数的关系，见表 1。表 1 系统控制参数 h 与 Lyapunov 指数的关系 Tab.1 The relationship between system control parameter h and Lyapunov exponent 密文图像。具体流程见图 1。解密过程与加密过程相反，这里不再赘述。图 1 图像加密流程 Fig.1 Image encryption process 2.1 第 1 次置乱置乱操作只扰乱图像各个像素点的位置，而不改变各个像素点的值。置乱过程如下所述。 1）引入四阶龙格-库塔方程对式（1）进行离散并得到一个伪随机浮点数序列 s。四阶龙格-库塔离散形式为： 1 1 i i 3 4 2 i i i 2 3 i i f f ( ) 1  2         ) 1 (3) y y h ( 6 K f ( ) h 2 h 2 h K K K K K K K 2  yx , (  h y x ,  2 h y x 2 y x h (               2）将步骤 1）得到的伪随机序列 s 转换为一维整数序列 X，获取明文图像 P 的尺寸 M×N，将明文图像 P 的任一点坐标（i,j）进行 Arnold 变换，经过迭代运算后得到的 p, q 与伪随机序列 X 的元素进行模运算得到新的坐标(p, q)。Arnold 变换公式为： K K K    ) ) f i i , , 2 3 4 i  1 1   1 2  X i ( ( )  X i ( ) (  p     q   p (5)  q (6)  对明文 P 的像素点 P（i,j）与P（p,q）进行对换， i       j    p ) mod( q ) mod( M N )  M N )  (4) 完成置乱得到矩阵 B。 h Lyapunov指数 L1 L2 L3 系统状态 2.2 第 1 次扩散 2.8 2.102897 5.0 1.814621 8.0 0.848959 0.002314 0.003568 −0.000682 −14.305211 −16.218189 −18.248277 混沌混沌混沌文中的图像加密系统采用 h=2.8 ，与经典的 Lorenz 系统相比，具有更大的 Lyapunov 指数，其混沌行为也更为复杂。 2 图像加密系统首先引入混沌系统式（1）和四阶龙格-库塔方程对明文图像进行离散并引入 Arnold 映射进行第 1 次置乱，将置乱后的图像进行“异或”的扩散处理，再引入二维 Logistic 混沌系统对图像进行第 2 次置乱，最后将置乱后的图像进行“循环移位”的扩散处理，形成扩散是不改变像素点的位置，只改变像素点的值的过程。第 1 次扩散包括正向和逆向 2 次运算[11]。将置乱的图像 B 展开为一维矩阵 K。C 为长度是 M×N 的一维矩阵，初始值为 0。S 为由 X 与256 进行模运算生成的中间密文，通过正向扩散和逆向扩散 2 次运算，将每个明文像素点的值隐藏到了密文的每个像素点中，扩散后的矩阵记为 C。 i i i i i 1    S K   C C S  正向（按 i 从 1 到 M×N）的算法为： C C K 逆向（按 i 从 M×N 到 1）的算法为： C C C K S K   C S      1  1  1  i i i i i i i i i i i (7) (8) (9) (10)

第 39 卷第 5 期徐扬等：一个切换 Lorenz 混沌系统在图像加密中的应用 ·181· 2.3 第 2 次置乱 3.1 密钥空间分析借助于二维 Logistic 映射对矩阵 C 进行置乱[11]，将置乱后的矩阵记为 D。二维 Logistic 映射为： ux n x n 1) (   y n ( 1) 1     2 x n ( )] y n ( ) ( )[1    3.5695 1.4 u   2    4 (11) 2.4 第 2 次扩散对矩阵 D 进行循环左移位的运算[12]。循环左移位的运算公式为： S ( D i i i i  i   1  ( 1 P ) i S     D (12) i D D D ) i (13) 式中：LSB3 表示取数据的最低 3 位。最终得到加 LSB D ) ( i 1  ) mod 256  LSB D i P i   1 1  ( 3 3 密图像 D。 3 图像加密系统性能测试选用灰度图像 Lena、Camera 和 Peppers 作为加密测试对象，测试环境：CPU 为 Intel Core I5-3450，内存 32 G，操作系统为 Win7 专业版，Matlab 2012b。密钥 Key={x0, y0, z0, n}，其中 x0, y0, z0 为式（1）的初始值，n 为迭代次数。经过图像加密系统的运行，明文 Lena 图像的加密效果见图 2—4。 a 明文图像 b 密文图像 c 还原图像图 2 Lena 图像加密效果 Fig.2 Lena image encryption effect a 明文图像 b 密文图像 c 还原图像图 3 Camera 图像加密效果 Fig.3 Camera image encryption effect a 明文图像 b 密文图像 c 还原图像图 4 Peppers 图像加密效果 Fig.4 Peppers image encryption effect 一个良好的图像加密系统必须具备足够大的密钥空间来抵抗针对密钥的暴力攻击，当密钥空间大于 2100 才能为加密系统提高安全可靠的保障[13]。文中加密系统的密钥 Key={x0, y0, z0, n}，其中 x0, y0, z0 都是 double 型浮点数，n 为整数。在 64 位 CPU 的计算机下运行，密钥分量 x0, y0, z0 的浮点数精度都可达到 10−14 ，密钥空间可达到 1014×1014×1014× 1014=1056，远远大于 2100≈1.27×1030，可以确定加密系统具有足够大的密钥空间，完全能够抵御针对密钥的暴力攻击。 3.2 直方图分析图像的直方图能够表达出图像的一般规律性，能够直观地看出图像质量特性的分布状态。测试图像及其密文图像的直方图见图 5—7。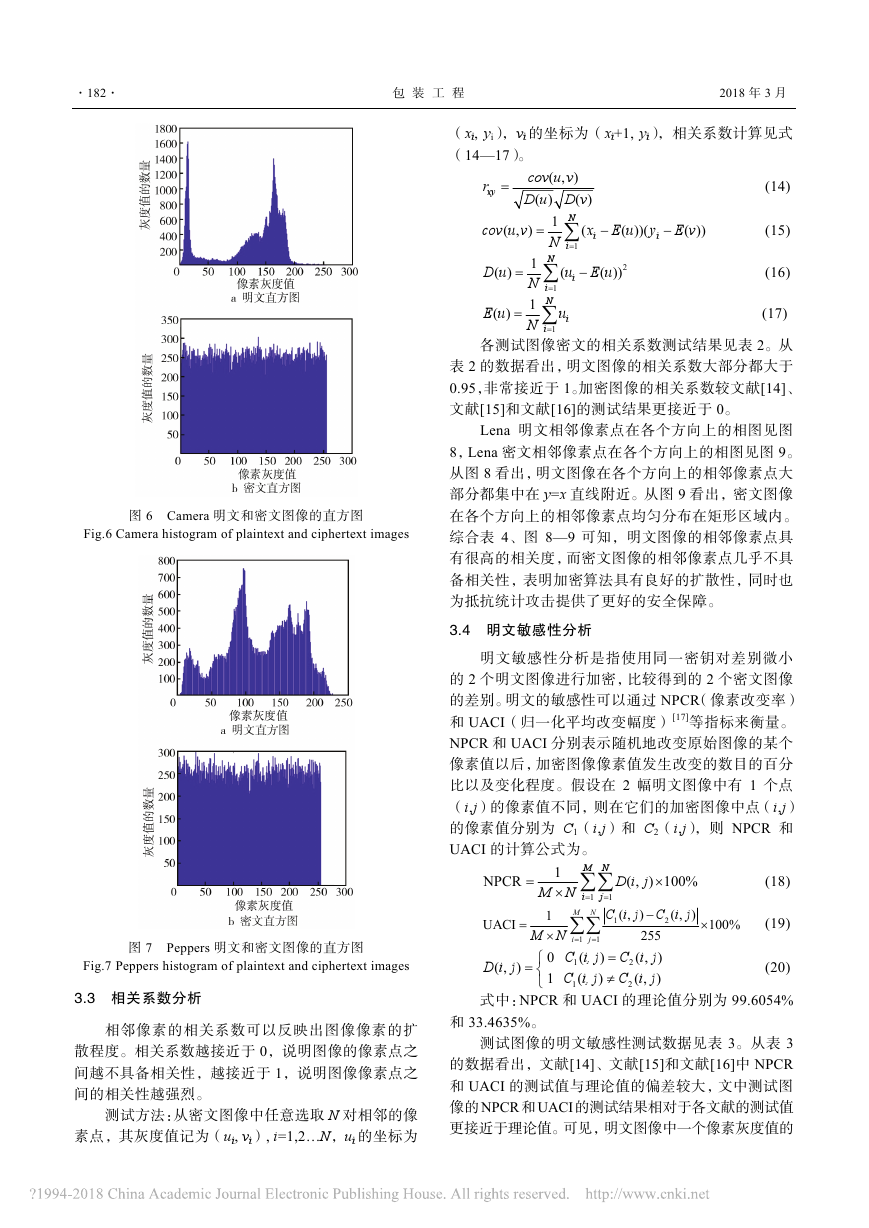从图 5—7 看出，明文的直方图波动范围较大，波峰波谷之间的差值较大，可以准确地反映各像素值的频率分布。密文的直方图基本上均匀分布在一个矩形区域内，不依赖于明文，各像素值出现的频率基本相同。表明图像加密后，像素点基本属于均匀分布，有效地掩盖了原始图像各像素的分布规律，扰乱效果理想，可以有效地防止统计分析的攻击。图 5 Lena 明文和密文图像的直方图 Fig.5 Lena histogram of plaintext and ciphertext images

·182· 包装工程 2018 年 3 月（xi, yi），vi 的坐标为（xi+1, yi），相关系数计算见式（14—17）。 (14)  E u ( ))( y i  E v ( )) (15) E u ( )) 2 (16) r xy  cov u v ( , ) D u ( )  x i (  cov u v ( , ) D u D v ( ) ( ) 1 N  N  i 1 1 N  u ( N  i 1 1 N N  i 1 u i i E u ( )   (17) 各测试图像密文的相关系数测试结果见表 2。从表 2 的数据看出，明文图像的相关系数大部分都大于 0.95，非常接近于 1。加密图像的相关系数较文献[14]、文献[15]和文献[16]的测试结果更接近于 0。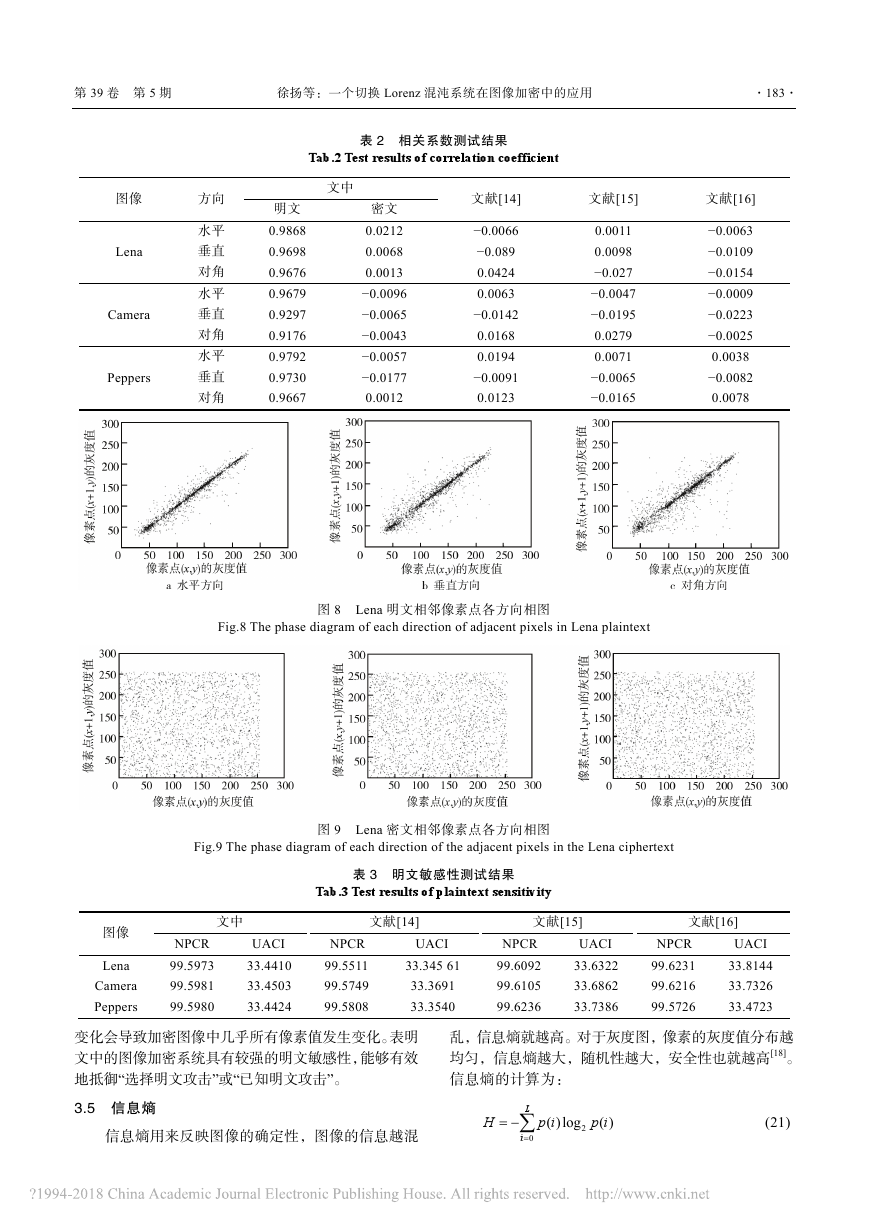图 6 Camera 明文和密文图像的直方图 Fig.6 Camera histogram of plaintext and ciphertext images Lena 明文相邻像素点在各个方向上的相图见图 8，Lena 密文相邻像素点在各个方向上的相图见图 9。从图 8 看出，明文图像在各个方向上的相邻像素点大部分都集中在 y=x 直线附近。从图 9 看出，密文图像在各个方向上的相邻像素点均匀分布在矩形区域内。综合表 4、图 8—9 可知，明文图像的相邻像素点具有很高的相关度，而密文图像的相邻像素点几乎不具备相关性，表明加密算法具有良好的扩散性，同时也为抵抗统计攻击提供了更好的安全保障。 3.4 明文敏感性分析明文敏感性分析是指使用同一密钥对差别微小的 2 个明文图像进行加密，比较得到的 2 个密文图像的差别。明文的敏感性可以通过 NPCR（像素改变率）和 UACI（归一化平均改变幅度）[17]等指标来衡量。 NPCR 和 UACI 分别表示随机地改变原始图像的某个像素值以后，加密图像像素值发生改变的数目的百分比以及变化程度。假设在 2 幅明文图像中有 1 个点（i,j）的像素值不同，则在它们的加密图像中点（i,j）的像素值分别为 C1（i,j）和 C2（i,j），则 NPCR 和 UACI 的计算公式为。 1 M N   M N  i 1 1  C i 1 M N   1 M N  i j 1 1  C i, j ) ( 0  1   C i, j 1 ( )  1 j C i  255 j ( , ) j ( , ) ( , ) 100% C i 2 C i (20) NPCR D i j ( , ) (18) UACI  100% (19) j ( , ) 2 ( , ) D i j      2 j 式中：NPCR 和 UACI 的理论值分别为 99.6054% 和 33.4635%。测试图像的明文敏感性测试数据见表 3。从表 3 的数据看出，文献[14]、文献[15]和文献[16]中 NPCR 和 UACI 的测试值与理论值的偏差较大，文中测试图像的NPCR 和UACI 的测试结果相对于各文献的测试值更接近于理论值。可见，明文图像中一个像素灰度值的图 7 Peppers 明文和密文图像的直方图 Fig.7 Peppers histogram of plaintext and ciphertext images 3.3 相关系数分析相邻像素的相关系数可以反映出图像像素的扩散程度。相关系数越接近于 0，说明图像的像素点之间越不具备相关性，越接近于 1，说明图像像素点之间的相关性越强烈。测试方法：从密文图像中任意选取 N 对相邻的像素点，其灰度值记为（ui, vi）, i=1,2…N，ui 的坐标为

第 39 卷第 5 期徐扬等：一个切换 Lorenz 混沌系统在图像加密中的应用 ·183· 表 2 相关系数测试结果 Tab.2 Test results of correlation coefficient 图像 Lena Camera Peppers 方向水平垂直对角水平垂直对角水平垂直对角文中密文 0.0212 0.0068 0.0013 −0.0096 −0.0065 −0.0043 −0.0057 −0.0177 0.0012 明文 0.9868 0.9698 0.9676 0.9679 0.9297 0.9176 0.9792 0.9730 0.9667 文献[14] 文献[15] 文献[16] −0.0066 −0.089 0.0424 0.0063 −0.0142 0.0168 0.0194 −0.0091 0.0123 0.0011 0.0098 −0.027 −0.0047 −0.0195 0.0279 0.0071 −0.0065 −0.0165 −0.0063 −0.0109 −0.0154 −0.0009 −0.0223 −0.0025 0.0038 −0.0082 0.0078 图 8 Lena 明文相邻像素点各方向相图 Fig.8 The phase diagram of each direction of adjacent pixels in Lena plaintext Fig.9 The phase diagram of each direction of the adjacent pixels in the Lena ciphertext 图 9 Lena 密文相邻像素点各方向相图表 3 明文敏感性测试结果 Tab.3 Test results of plaintext sensitivity 图像 Lena Camera Peppers 文中文献[14] 文献[15] 文献[16] NPCR 99.5973 99.5981 99.5980 UACI 33.4410 33.4503 33.4424 NPCR 99.5511 99.5749 99.5808 UACI 33.345 61 33.3691 33.3540 NPCR 99.6092 99.6105 99.6236 UACI 33.6322 33.6862 33.7386 NPCR 99.6231 99.6216 99.5726 UACI 33.8144 33.7326 33.4723 变化会导致加密图像中几乎所有像素值发生变化。表明文中的图像加密系统具有较强的明文敏感性，能够有效地抵御“选择明文攻击”或“已知明文攻击”。乱，信息熵就越高。对于灰度图，像素的灰度值分布越均匀，信息熵越大，随机性越大，安全性也就越高[18]。信息熵的计算为： 3.5 信息熵信息熵用来反映图像的确定性，图像的信息越混 H L   i  0 p i ( )log 2 p i ( ) (21)

·184· 包装工程 2018 年 3 月式中：L 为图像的灰度等级数；p（i）为灰度值 i 出现的概率。对于 L=256 的灰度图像来说，信息熵的理论值 H≤8。信息熵越接近于理论值，图像被攻击的可能性越小。测试图像密文的信息熵测试结果见表 4。从表 4 看出，文中加密图像的信息熵与文献[14]和文献[15] 的测试结果相比，更接近于理论值 8，表明加密系统的算法随机性良好，加密后图像的混乱程度很高，由密文图像无法得到明文图像的任何信息。表 4 信息熵测试结果 Tab.4 Test results of information entropy 图像 Lena Camera Peppers 文中 7.9973 7.9973 7.9970 文献[14] 7.9951 7.9960 7.9965 文献[15] 7.9965 7.9959 7.9958 4 结语将一种新的切换 Lorenz 混沌系统引入到图像加密系统中，通过“置乱-扩散-置乱-扩散”的过程，结合 Logistic 混沌映射，完成了图像的加密。通过理论分析和仿真测试，加密图像的相关系数、明文敏感性以及信息熵等测试结果都非常接近于理论值，表明文中的图像加密算法具有较强的鲁棒性，能够有效地抵抗常见的攻击手段，在图像加密、通信等领域具有较好的应用前景。参考文献： [1] MATTEWS R. On the Derivation of a “Chaotic Encryp- tion Algorithm”[J]. Cryptologia, 1989, 13(1): 29— 42. [2] CHEN G R, MAO Y, CHUI C K. A Symmetric Image Encryption Scheme Based on 3D Chaotic Cat Maps[J]. Chaos, Solitons and Fractals, 2004, 21(3): 749—761. [5] [4] [3] MAO Y, CHEN G R, LIAN S. A Novel Fast Image Encryption Scheme Based on 3D Chaotic Baker Maps [J]. International Journal of Bifurcation and Chaos, 2004, 14(10): 3613—3624. Image Encryption ZHANG Y. Plaintext Related Scheme Using Chaotic Map[J]. Telkomnika, 2014, 12 (1): 635—643. ZHANG Y, XIA J, CAI P, et al. Plaintext Related Two-level Secret Key Image Encryption Scheme[J]. Telkomnika, 2012, 10(6): 1254—1262. ZHANG Y. A Chaotic System Based Image Encryption Algorithm Using Plaintext-Related Confusion[J]. Telkomnika, 2014, 12(11): 7952—7962. ZHANG Y. The Image Encryption Algorithm With Plaintext-Related Shuffling[J]. IETE Technical Re- view, 2015, 33(3): 310—322. [6] [7] [8] 卢辉斌, 张鹏, 国宪鹏, 等. 一种新的基于双混沌系统的图像加密方案[J]. 计算机工程与应用, 2012, 48 (2): 90—92. LU Hui-bin, ZHANG Peng, GUO Xian-peng, et al. New Image Encryption Theme Based on Dual Chaotic Systems[J]. Computer Engineering and Applications, 2012, 48(2): 90—92. [9] 刘乐鹏, 张雪锋. 基于混沌和位运算的图像加密算法[J]. 计算机应用, 2013, 33(4): 1070—1073. LIU Le-peng, ZHANG Xue-feng. Image Encryption Algorithm Based on Chaos and Bit Operations[J]. Journal of Computer Applications, 2013, 33(4): 1070— 1073. [10] 王忠林, 刘树堂. 一个切换 Lorenz 混沌系统的特性分析[J]. 重庆邮电大学学报(自然科学版), 2017, 29 (1): 68—74. WANG Zhong-lin, LIU Shu-tang. Analysis of Proper- ties of a Switched Lorenz Type Chaotic System[J]. Journal of Chongqing University of Posts and Tele- communications(Natural Science Edition), 2017, 29 (1): 68—74. [11] 张永红, 张博. 基于 Logistic 混沌系统的图像加密算法研究[J]. 计算机应用研究, 2015, 32(6): 1770—1773. ZHANG Yong-hong, ZHANG Bo. Algorithm of Image Encrypting Based on Logistic Chaotic System[J]. Appli- cation Research of Computers, 2016, 32(6): 1170— 1173. [12] 张勇. 混沌数字图像加密[M]. 北京: 清华大学出版社, 2016. ZHANG Yong. Chaotic Digital Image Cryptosystem [M]. Beijing: Tsinghua University Press, 2016. [13] NOROUZI B, SEYEDZADEH S M, MIRZAK- UCHAKI S, et al. A Novel Image Encryption Based on Row-Column, Masking and Main Diffusion Processes with Hyper Chaos[J]. Multimedia Tools and Applica- tions, 2013, 74(3): 781—811. [14] WANG Xing-yuan, LIU Lin-tao, ZHANG Ying-qian. A Novel Chaotic Block Image Encryption Algorithm Based on Dynamic Random Growth Technique[J]. Op- tics and Laser in Engineering, 2015, 66: 10—8. [15] HUA Zhong-yun, ZHOU Yi-cong, PUN C M, et al. 2D Sine Logistic Modulation Map for Image Encryption [J]. Information Sciences, 2015, 297: 80—94. [16] WANG X Y, YANG L, LIU R, et al. A Chaotic Image Encryption Algorithm Based on Perceptron Model[J]. Nonlinear Dyn, 2010, 62(3): 615—621. [17] 王静, 蒋国平. 一种超混沌图像加密算法的安全性分析及其改进[J]. 物理学报, 2011, 60(6): 83—93. WANG Jing, JIANG Guo-ping. Cryptanalysis of a Hy- per-chaotic Image Encryption Algorithm and Its Improved Version[J]. Acta Phsica Sinica, 2011, 60(6): 83—93. [18] 林青, 王延江, 王珺. 基于超混沌系统的图像加密算法[J]. 中国科学(技术科学), 2016, 46(9): 910—918. LIN Qing, WANG Yan-jiang, WANG Jun. The Image Encryption Scheme With Optional Dynamic State Var- iables Based on Hyperchaotic System[J]. Scientia Sinica Technologica, 2016, 46(9): 910—918.

分享到：

赞收藏

资料库

图像混沌加密.pdf

相关推荐

信息化

热门标签

最新资料