进化算法的自适应加速 .pdf-资料库

http://www.paper.edu.cn 进化算法的自适应加速李逸飞武汉工业学院 430021 E-mail：myliyifei@126.com 摘要：本文针对非线性函数优化问题，提出一种带有基因交流机制的多群体进化算法。该算法采用随机、置换、逆序、融合等七种进化算子，并利用统计计算、弹性搜索以及灾难因子构成自适应加速机制。经实例测算，算法效果显著。关键词：进化算法自适应加速 1. 引言许多工程实际问题都可归结为非线性函数优化问题，非线性优化问题的数学模型一般表示为： j n Xf ) ( min Xg ( ) ≤ Xh s.t. ) ( = k x x 1 ≤ ≤ i i RX j ,2,1 0 k ,2,1 0 x i u ,2,1 i ∈ = = = , L , L , p q n L 上式含有不等式与等式约束条件，可以应用罚函数法将上述问题转化为 XF ( ) = Xf ( ) + b p ∑ { i = 1 ,0max[ Xg i ( )] + q ∑ j = 1 | Xh j ( }|) ,其中罚因子 0>b 。一般来说，上述问题总可以转换为下列问题： ∈ xRXXF , 1 i min ) ( n ≤ x i ≤ x u i i ,2,1 L= , n 求解非线性问题的传统优化算法有牛顿法、梯度法等，但是实践中非线性优化问题常为多极值问题，传统优化算法难以求解。近年来发展起来的遗传算法、微粒群算法等群体性迭代算法在求解多极值问题上有所进展，但存在的缺点是计算量较大、效率不高。[1][2][3] 在考察各种群体性迭代算法之后，发现这类算法尚未充分利用在计算过程中产生的大量信息。对此问题，本文提出一种自适应加速方式，为提高此类算法计算效率提供了一种有效途径。 2. 进化算法本文的基础算法是进化算法(也称进化计算，下文简称 EC)，EC 是借鉴生物进化机制的一种优化算法。 EC 编码方式：将 n 维设计向量 X 看作生物个体，个体向量中的每一个分量看作其相应个体的基因，以此做为 EC 的编码基础。个体适应度：直接采用目标函数值，对于最小值问题此数值越小越好。 - 1 -

http://www.paper.edu.cn 且 EC进化算子选择策略：采用轮盘赌方式。共采用 7 个算子，相应给定概率 P ~ 6 P + 1 P 0 P 0 EC 父代个体选择策略：取决于个体在父代群体中的排名序号，即根据个体 i 在总数为 P 1 = + + L 6 PPr ≤< + 2 ，EC首先产生一个 0 到 1 之间的随机数r,若 + ，则选择第i号算子。[2] P 0 + + P i , + P 1 L L P i + 1 − 1 m 的父代群体中的排名来分配其选择概率，第 i 个个体被选择的概率为 1 − i + 1 m ，这样因性状良好而排在前面的个体被选中的概率更大。 EC 子代筛选策略：采用“精英保留”策略。若精英群体的数量为 m，根据子代个体的适应度具体分为三种情况处理，设 f 为当前新子代个体适应度，的适应度： A 若 f ≤ 1f f ,1 L , mf 依次为父代个体，则此子代个体取代精英群体的 1 号个体，原精英群体个体序号位置依次后移 1，丢弃最后序号个体； B 若 f <1 f ≤ mf ，则此子代个体随机替换精英群体序号 4 到 m 之间的一个父代个体； C 若 f > mf ，则此个体不进入精英群体。 EC 的进化算子：设 h、l 为变量的可行区间上、下限；X 为子代个体向量；A、B 为父代个体的向量；Random 为 0 到 1 之间的随机数。 1．随机创生：在动态搜索区间上随机产生子代个体，则子代个体基因为 x i = ( h i − l i ) × Random , i ,2,1 L= , n ； 2．截尾变异：子代个体所有分量只保留前 2 至 4 位有效数字，截去尾部其它数字 ⎦ µµ /A ⎣ 3．逆序变异：随机选择一个父代个体，然后将其全部分量次序颠倒，即；为一个随机整数，则 ,100[∈µ 10000 X = 令 ] 设父代 A a [ 1 L= , , na ] ，则子代 X [ n L= a , , 1a ] ； 4．对称变异：在所选的父代个体中随机选择若干个基因，则子代个体基因为 x i += l (η aH − i 1,) ≤≤ i n ，η＝0.9995； 5．置换交叉：选择两个父代个体 A 和 B，子代个体基因以 1/2 的概率随机选取两者之一的基因组成，即 Random Random = a b i ⎧ ⎨ ⎩ , , i i x < ≥ 5.0 5.0 ； 6．融合交叉：选择两个父代个体 A 和 B，则子代个体基因为 ≤≤ Random Random 1( ), − + × = a 1 x i i i b i n 7．逆序交叉：选择两个父代个体 A 和 B，随机产生 i、j 且满足 1 < i < j < n，即 A B = = [ [ a , 1 b , 1 L L aa , i bb , i i i , 1 + , a L b L 1 + j 1 − , j 1 − a , b j j , , a L b n L ] n ] - 2 -

http://www.paper.edu.cn 则子代为: X = [ a 1 , a i 1 − , bb , j j 1 − , L , b i 1 + , ab i , L , L a n ] j 1 + EC 采用多群体结构，这样可以根据问题的难易程度，选择任意数量的子群。在进化过程中，各子群独立进化，经过给定代数之后，子群之间再发生基因交流，具体形式如下：各子群之间发生基因交流，一个种群的前 50％的个体与另一个种群前 50％的个体奇偶交错排列组成新种群。以三个子群 A、B、C 为例，每个子群有四个个体，即 A: B: C: 2 3 AAAA 1 4 BBBB 1 CCCC 1 4 3 2 4 3 2 ；；；发生基因交流之后，重新组合的子群为： A： B： C： 2 1 2 BABA 1 CBCB 1 2 ACAC 1 2 2 1 2 1 ；；；终止条件：因为 EC 为迭代型算法，必须设置适当的终止条件。本文采取以下终止条件：符号说明：为第 i 代最优向量的分量 X i − 1． 2． 3． ( S D 停滞迭代 ( ( ) i 1 − ≤ − f ) f ) x < f i > 迭代停滞 Z E E F i 。；； fE and and X ≤ i 1 − S max > D max iX fi为第i代最优函数值 xE 与为给定设计向量与目标函数的精度 Fi为第i代最好目标函数值 Z 为第 i 代之前的最好目标函数值停滞S 为计算过程中迭代结果连续没有改进的累计次数停滞Smax 停滞D 迭代Dmax 为给定的最多连续停滞次数为给定最大进化代数为进化代数 EC 算法步骤：1.初始化，随机产生给定数量的各子群个体； 2.利用轮盘赌方式选择子代个体产生方式； 3.根据选定方式，调用进化算子产生子代个体； 4.将子代个体的适应度与精英群体比较，执行“精英保留”策略； 5.完成子群循环后，所有子群之间进行基因交流； 6.检查终止条件，满足则退出，否则转向 2。 - 3 -

http://www.paper.edu.cn 3. 自适应加速在传统优化算法感到困难的多极值问题上，进化类算法获得了一定的改进，但同时也伴随有计算量偏大的缺陷。在前文提出的 EC 中，我们注意到 EC 并没有充分利用计算过程中得到的相关进化信息。下文提出一种加速思路，将此思路和 EC 结合构成自适应加速进化算法（以下简称 AEC）。 AEC 的具体内容叙述如下：进化过程中保留的精英群体，其个体位置可能提供了全局最优解的范围信息，我们可以对其进行统计计算，由此获得信息数值，用于缩小下一轮进化计算的搜索区域。设精英群体为 XX , 1 L, nX 2 ，其分量的标准差为： σ j = 1 − m 1 其中 x j = m ∑ i 1 = 1 m m ∑ i 1 = ( x ji − x ,) 2 j j = ,2,1 , n L x ji j x + = 2 σ j 那么下一轮搜索区域缩小为： h 2 σ j 其中，h、l分别为分量搜索区间的上、下限；xj1为 1 号最优个体的分量。引进上述加速方式后，搜索区域将随进化过程缩小，从而导致迭代过程加快。但是对于 ,2,1 L= 。 − = n x l j , , , 1 j 1 j j 多极值问题，此加速方式加大了陷入局部极值的概率。为了消除这种影响，在上述加速方式的基础上同时使用另外两个机制，使得整个加速过程具有自适应性质。 1．弹性缩放在计算过程尚未达到终止条件之前，若个别分量的搜索区域已经小于给定设计变量精度数值，则将其分量搜索区域放大 10 倍，即： j j 1 jnew x x = = h (5 + h (5 − h l jnew 其中,hnew、lnew分别为分量搜索区域更新后的上、下限，其余符号同上。 l − l − ) j ) 1 j j j 2．灾难因子在计算过程尚未达到终止条件之前，若停滞次数已达到给定次数，则将搜索区域恢复到问题的原始求解区域，并对每个子群第 3 到 n 号个体重新进行初始化处理，同时将每个子群的第 2 号个体基因替换为当前所有群体中最好的个体基因。加速机制、弹性缩放和灾难因子三者相配合，构成一套自适应加速机制。对相关文献 [3][4][5]中诸多经典测试问题进行实算，结果表明，AEC求解多极值问题有明显效果。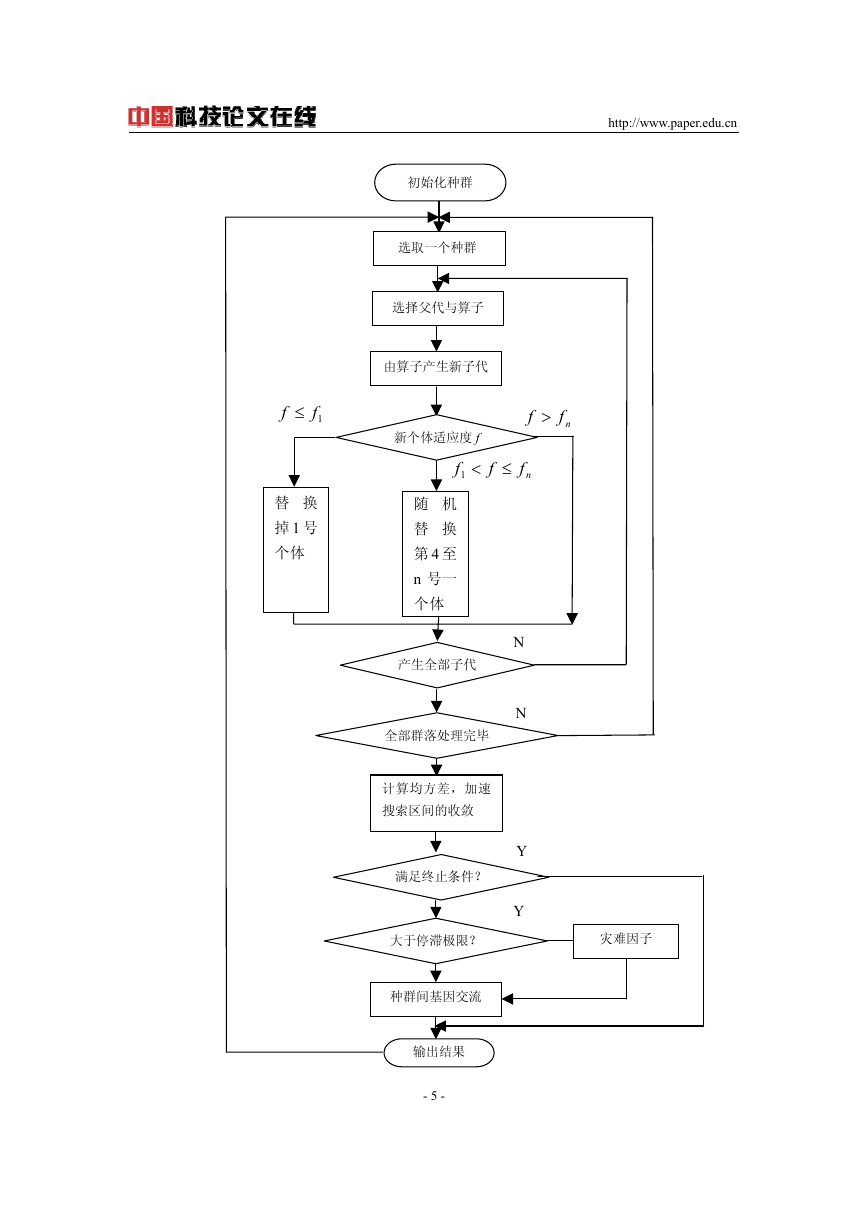 AEC 的流程图见下图： - 4 -

http://www.paper.edu.cn 初始化种群选取一个种群选择父代与算子由算子产生新子代 f ≤ 1f 替换掉 1 号个体新个体适应度 f <1 f f > nf f ≤ nf 随机替换第 4 至 n 号一个体产生全部子代全部群落处理完毕计算均方差，加速搜索区间的收敛满足终止条件？ N N Y Y 大于停滞极限？灾难因子种群间基因交流输出结果 - 5 -

4. 数值测试三道测试问题来源于文献[6]，均取n=50，设计变量范围取: f1:(-7.5,15), f2:(-7.5,15) , f3:(-300,600) http://www.paper.edu.cn xf )( 1 = f 2 x )( = n ∑ j 1 = 100[ ( x − x ) 22 j + ( x j − ])1 2 j 1 + n ∑ j 1 = [ x 2 j − 10 cos( x 2 π ) + ]10 j f 3 x )( = 1 4000 n j 1 = ∏∑ − x 2 j n j 1 = ⎛ ⎜ cos ⎜ ⎝ x ⎞ ⎟ +⎟ ⎠ j j 1 为了验证 AEC 的性能，选用了三个典型的非线性优化问题，同时为了加强比较性，加入经典微粒群算法（CPSO）做为比较。CPSO 具体参数如下： K = 2 −− C 2 C 2 − C 4 , cC 1 = + Vc , 2 max = ,2 c 1 = ,8.2 c 2 = ,3.1 N = 50 AEC 参数：随机创生：0.30 对称变异 0.10 截尾变异 0.10 逆序变异 0.10 置换交叉 0.15 融合交叉 0.10 逆序交叉 0.15 设计变量与目标函数的精度精度 1E-9，子群数量 3，子群个体数 10 表格说明：以自适应加速进化算法为基准，记录在最好结果下的目标函数被调用次数，然后以大致相同的被调用次数计算出 CPSO 和 EC 的结果。 f1 平均标准差最好 CPSO EC AEC 64.217790707 549.059857227 0.0000000 50.665538772 600.5022641877 0.0000000 0.001647383 0.00000000 0.0000000 函数调用次数 122050 121503 121503 f2 平均标准差最好 CPSO EC AEC 223.507632827 0.46315769 0.0000000 50.221319473 4.4350438344 0.0000000 123.508491516 0.00000000 0.0000000 函数调用次数 28050 27888 27888 - 6 -

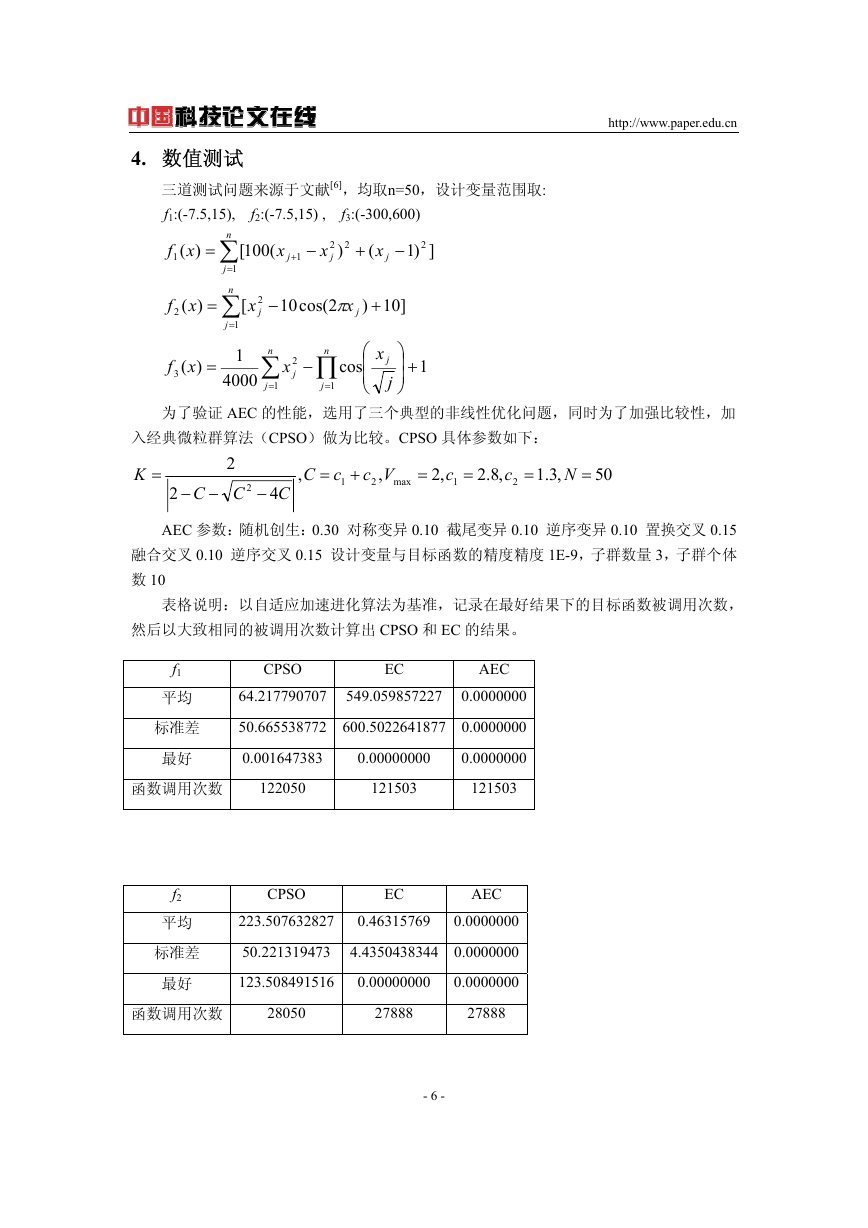
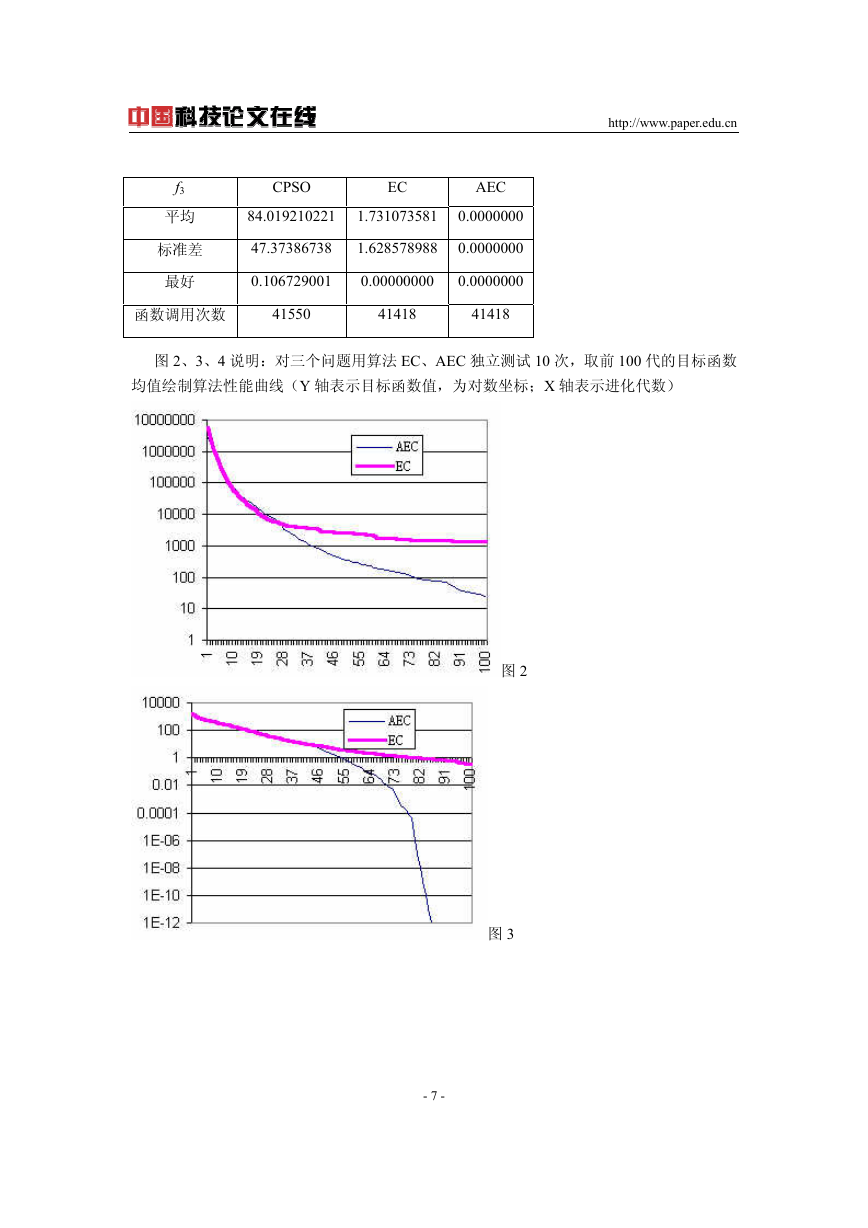
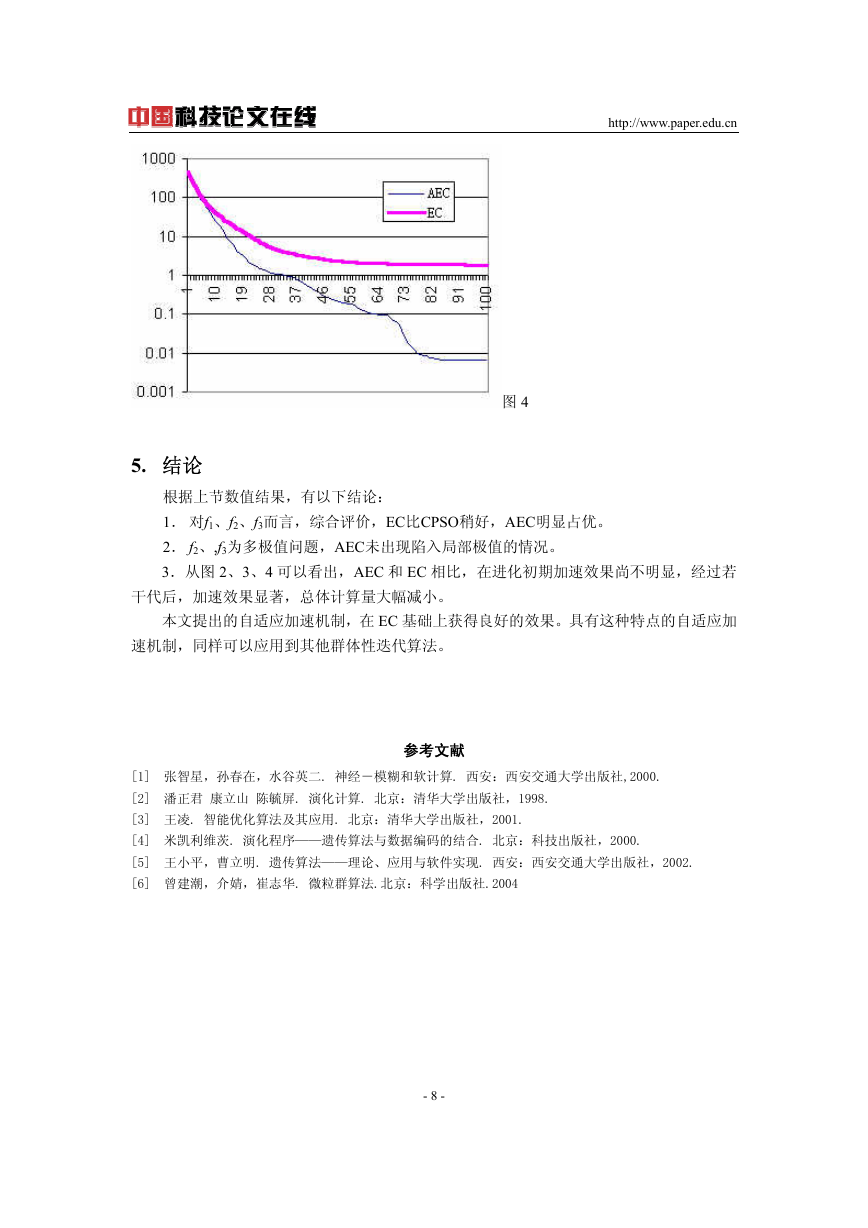
http://www.paper.edu.cn f3 平均标准差最好 CPSO EC AEC 84.019210221 1.731073581 0.0000000 47.37386738 1.628578988 0.0000000 0.106729001 0.00000000 0.0000000 函数调用次数 41550 41418 41418 图 2、3、4 说明：对三个问题用算法 EC、AEC 独立测试 10 次，取前 100 代的目标函数均值绘制算法性能曲线（Y 轴表示目标函数值，为对数坐标；X 轴表示进化代数）图 2 图 3 - 7 -

http://www.paper.edu.cn 5. 结论图 4 根据上节数值结果，有以下结论： 1．对f1、f2、f3而言，综合评价，EC比CPSO稍好，AEC明显占优。 2． f2、,f3为多极值问题，AEC未出现陷入局部极值的情况。 3．从图 2、3、4 可以看出，AEC 和 EC 相比，在进化初期加速效果尚不明显，经过若干代后，加速效果显著，总体计算量大幅减小。本文提出的自适应加速机制，在 EC 基础上获得良好的效果。具有这种特点的自适应加速机制，同样可以应用到其他群体性迭代算法。参考文献 [1] 张智星，孙春在，水谷英二. 神经－模糊和软计算. 西安：西安交通大学出版社,2000. [2] 潘正君康立山陈毓屏. 演化计算. 北京：清华大学出版社，1998. [3] 王凌. 智能优化算法及其应用. 北京：清华大学出版社，2001. [4] 米凯利维茨. 演化程序——遗传算法与数据编码的结合. 北京：科技出版社，2000. [5] 王小平，曹立明. 遗传算法——理论、应用与软件实现. 西安：西安交通大学出版社，2002. [6] 曾建潮，介婧，崔志华. 微粒群算法.北京：科学出版社.2004 - 8 -

资料库

进化算法的自适应加速 .pdf

相关推荐

开发技术

热门标签

最新资料