凸优化课程笔记.pdf-资料库

Chapter 2 Convex Set x 对于 1   x 2 nR 连接两点的直线可表示为 x | x  x  1 (1     x ) ,  2  R  [0,1] x  1 (1     x ) ,  2 C ，则连接两点的直线也在C 内 2   x | x x x 连接两点的线段可表示为 仿射集（Affine Set）定义：C 是仿射集↔ 1 , 例：线性方程组的解集是仿射集 C 证：线性方程组的解集可表示为一条直线是仿射集，一条线段则不是   平面是仿射集，一块矩形区域则不是  { x | Ax = b A ,  R m n  , b  R n } x x ,  设 1 2 C ，则 1Ax = b ， 1Ax = b  A x  1 (1   )  x  2   Ax + 1 (1  )  Ax 2  b  (1   )  b  b ，得证仿射组合（Affine Combination）  , ,   ,     k x ， 1 2      k 1 2 kx x 设 k 个点 1 , , , 2 R  1 x 则称 1 1   2  x 2    k x 为 1 k kx x , , , 2 x 的仿射组合仿射包（Affine Hull）任意集合 nRC ，C 中任意元素的仿射组合构成的集合称仿射包 C aff    x    1 1 2    x 2     k x k 2  x x x C , , ,    k 1   R , , ,       k 2 1   1         k 1 2 如果一个集合的仿射包就是它自己，那么它就是一个仿射集

C ，则连接两点的线段也在C 内 2 平面是凸集，一块矩形区域也是凸集    x x 凸集（Convex Set）定义：C 是仿射集↔ 1 , 凸组合（Convex Combination）  , [0,1] ,     k x ， 1 2  1       k 1 2 一条直线是凸集，一条线段也是凸集 kx x 设 k 个点 1 ,  , , , 2 x 则称 1 1   2  x 2    k x 为 1 k kx x , , , x 的凸组合 2 凸包（Convex Hull）任意集合 nRC ，C 中任意元素的凸组合构成的集合称凸包 C conv    x    1 1 2    x 2     k x k ,  C x x x , ,    k 1 2   [0,1] , , ,       k 1 2   1         k 1 2 一个凸集，它的凸包就是它本身凸集非凸集非凸集凸集的凸包（本身）非凸集的凸包

2  x x 凸锥（Convex Cone）定义：C 是仿射集↔ 1 , 凸锥组合（Convex Cone Combination）     设 k 个点 1 0 kx x 过原点的射线是凸锥 x ， 1 , , , , , , 2 2 k C ，对 1   2 , x  ，有 1 1   2 0 x 2  C 过原点的两条射线之间的区域是凸锥 x 则称 1 1   2  x 2    k x 为 1 k kx x , , , 2 x 的凸锥组合凸锥包（Convex Cone Hull）任意集合 nRC ，C 中任意元素的凸锥组合构成的集合称凸锥包 C     0    , x x x  k 1 ,     k 1  , ,  , , 2 k 2 2 x x     k    x    1 1 2   一个凸锥集，它的凸锥包就是它本身

凸集 √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ 仿射集 √ √ x  (1 )   √ √ √ × × √ × √ × × 凸锥 x  x √ √ × × × × × √ √ × ( a a , 1 2 ) x 1 x 2        b  P正定 , n n R R , , b R }  b R }  , x c  R ,n  r R 1  P x x  ( )  r , x  c c n R r R , （很多超平面和半空间的交集）      n n  |  A = A T 集合名称 1. 空集 2. 1 个点 3. nR 空间 4. nR 空间的子空间：{ x | Ax = }0 5. 任一直线 6. 任一线段 7. 任一射线： x 0    v |  0 8. 超平面：{ x | a x = T b , x  n R b R } , c c   T T , , { { b b   9. 半空间： x | a x x | a x x x 10. 欧几里得空间中的球： B x r ( x x x r , )    || || 2 c  11. 欧几里得空间中的椭球： E x ( x x x ) T P   r ) ( , , c  x  P       12. 多面体（Polyhedron）：  m , 1,   j n 1, ,   b a x T i i c x = d T j 13. 对称矩阵： i , , A S  n j R  n    14. 对称半正定矩阵： S A R n n  | A = A A , T 15. 对称正定矩阵： S n   A R n n  | A = A A , T  0  0 10）证明：设 1 x x ,  2 B ，则 || || x 1 x 2   x c x c || 2 || 2   r r   x x ) (1 || ||       1 2 2   x x (1 ) ||       c 1   x x (1 || ||      c 2 1 r r r ) (1        x (1 )     c   x x ||  2 2  x x ) ||   c 2 c x c  || 2 || 2  ||  x  1 (1   )  x   x c 2

13）对称阵是仿射集，因而是凸集证明：设 1 A A S ，则 1 n T A , 2 A ， 2 1 T A A 2 对 R  ， A  1 (1   )  A 2 T   A  1 (1   )  A ，得证 2 14）对称半正定阵是凸锥，因而是凸集 A ， 2 1 A A S ，则 1 证明：设 1 n  T A , 2 T A A ，且对x ，有 2 x A x ， T  0 1 x A x T 2  0 对称已证明，现证明半正定，对x 和 1 14）对称正定阵是凸集   2 ,  ， 0 T x (   1 2 A 1  A x = x A x 2 1  1 ) T   2 x A x ，得证 T 0  2 证明：设 1 A A S ，则 1 n  T A , 2 A ， 2 1 T A A ，且对 2  x ，有 0 Tx A x > ， 0 1 Tx A x > 0 2 ，  x T A  1 (1   )  A x = x A x 2 1  T  (1   )  x A x > ，得证 T 0 2 对称已证明，现证明正定，对  x 和 0   [0,1]

保持凸集凸性的操作  交集（Intersection）若 1S ， 2S 为凸集，则 1 2S S 为凸集。若 S 为凸集，对 A  ，则  S 为凸集。 A   注：并集不能保持凸集的凸性  仿射函数（Affine Function）定义：对 dom nRx f x ， ( )  Ax + b A ,  R ,m n  b  R m f ，在称 : n mR R 是仿射的定理：若 f nS R 是凸的， : n mR R 是仿射的，则 S 在 f 下的映射 ( f S ) { ( ) |  f x x S 是凸的  } 同样，若 g nS R 是凸的， : n mR R 是仿射的，则 S 在 g 下的反映射 1( g  S ) { |  x g x ( )  S 是凸的 } S 仿射变换 f S ( ) 例：缩放   S { x x S 和位移  } | S a   { x + a x S 是保持凸性的  } | S 例：两个凸集的和 1  S 2  { x + y x S y S 是保持凸性的   } , | 1 2 解释如下，集合 1S 与集合 2S 的笛卡尔乘积 1 S  S 2  {( , x y ) | x S y S   , 1 } 2 是保持凸性的集合 1 2S S 在仿射变换 ( , f x y )   下 x y f S ( 1  S 2 )  S 1  S 依然是保持凸性的 2 例：线性矩阵不等式（LMI: Linear Matrix Inequality）： A x ( )  x 1 A 1    x n A n  ， , B A S （对称阵） B n i  类比一般的线性不等式（Linear Inequality）： a x T  x a 1 1    x a n n  b ib x ， , R ）求证：线性矩阵不等式 ( )A X B 的解集{ 证明： ( f X )  B A X  ( )  S n  是凸集 f 1(  X ) {  X B A X  ( | )  S 也是凸集 }n  X A X ( | ) B 是凸集 } 例：椭球是球的仿射映射，因此是凸的球 而 x u ( ) || x x (   u u R || 2   R  1, 1, u=P u u u   || || 1 2 n n 2 )  是凸的，它在仿射变换 c x u P ( ) ||       x u ( )  1 2 P u+ x 下 c x u ( ) || u || 2  1, u R n  也是凸的  1 2 ( x  x c ) || 2  1, u  R n x u P ( ) ||  1 2            ( x  x c ) || 2 2  1, u  R n      2 a|| || T a a   x u x x ( ) (  ) T c 1  P x x  ( ) 1,  u R n c  就是椭圆

 透视函数（Perspective Function）定义： P RP = ， dom Rn R : n 1 n  R z t  P z t ( , ) , z  n R t , R  （ R    t { R | t  ） 0}  定理：若 domC P 是凸集，则 ( P C ) { ( ) |  P x x C 也是凸集  } 例：考虑 1nR 内的一个线段设 x y    x ( ,  y ( , x n y n 1  1  ), ), x n y 1  n 1    0 0 ，则 1nR 内的一个线段可表示为 x  (1      y ) , [0,1] 该线段经透视变换后仍为线段 (1   (1    x  x  n  P x  (1   )   y  1  )  )   y y n x  n 1  (1 )    1   x y n 1  x n 1  + (1 y )   n 1  ) (1    x  n 1   x  n  y y n 1  y n 1    x  n 1  1  x  n 1  (1 )     [0,1]  y n 1    P x  (1   )   P y   线性分数函数（Linear-fractional Function） n mR 1 R g x 满足 ( ) A c T        x + b d       ， A R m n  c R n d ,  b ,   R m R 设仿射函数 g : 设透视函数 P : m  R 1 m R t 满足 ( , ) P z  f 定义线性分数函数 : n mR R 满足 f R  m R t , , z  z t P g ，即 f x ( )   P g x ( )   P Ax + b   c x d T      Ax + b c x d T  dom { | x c x  f T 例：两个随机变量的联合概率与条件概率设两个离散型随机变量（Random Variable） :{1, U n ， :{1, , } V 联合概率： ijp  P U i V { ,   ；条件概率： j } q ij  P U i V {  |   d 0} m , }  j }  P U i V , {   P V {  j } j }  p ij  p kj n k 1  设 p  p 1  p m                       p 11  p n 1  p m 1  p nm            ， q q 1   q      m                  q 11  q n 1  q m 1  q nm            I j  ( 0 0  ， e j  (0 0  { }jq 是凸集，{ }q 是凸集  j I  n n  th block  1 1  j th block, n 1s 0 ) nm n   0) nm 1  ，于是 q j  f p ( )  I p j e p j

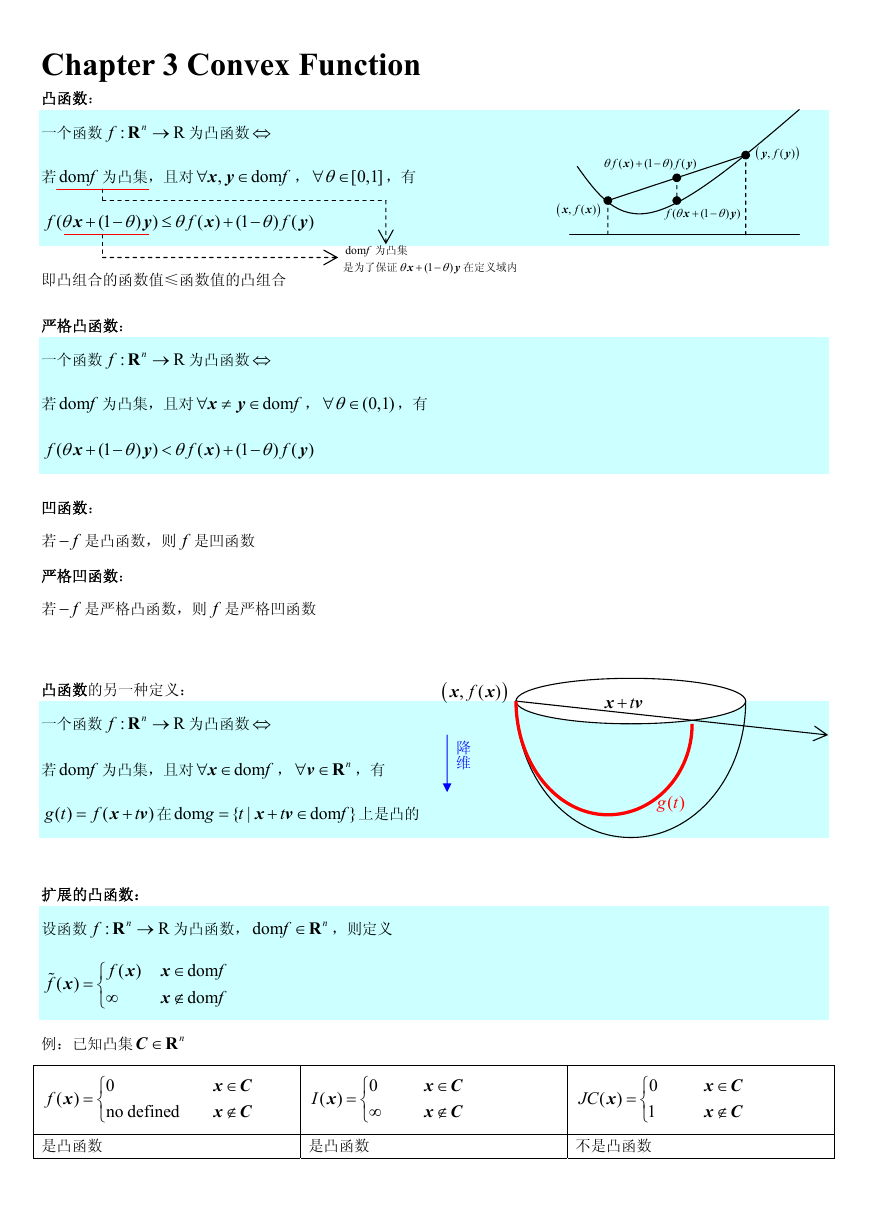
Chapter 3 Convex Function 凸函数： f 一个函数 : n R R 为凸函数  若 domf 为凸集，且对 , x y  domf ，   [0,1] ，有 f  x ( ) )   (1 f y ( )  fy , y ( )   fx , x ( )  x f  ( domf 为凸集 x  是为了保证 )   (1 y 在定义域内 f x (  (1    y ) )  f  x ( ) (1   )  f y ( ) 即凸组合的函数值≤函数值的凸组合严格凸函数： f 一个函数 : n R R 为凸函数    (1 y ) ) 若 domf 为凸集，且对    x y domf ，   (0,1) ，有 f x (  (1    y ) )  f  x ( ) (1   )  f y ( ) 凹函数：若 f 是凸函数，则 f 是凹函数严格凹函数：若 f 是严格凸函数，则 f 是严格凹函数凸函数的另一种定义： f 一个函数 : n R R 为凸函数  若 domf 为凸集，且对  x domf ，  Rv n ，有 g t ( )  f ( x t v 在 dom { | t ) g  x   v t f dom } 上是凸的  fx , x ( )  降维 tx v ( )g t 扩展的凸函数： R f 设函数 : n R 为凸函数， dom f R ，则定义 n  f x ( ) x ( ) f     x x   f dom f dom 例：已知凸集 nRC 0 no defined f x ( )     是凸函数 x C  x C  I x ( ) 0     是凸函数 x C  x C  JC x ( ) 0    1  不是凸函数 x C  x C 

资料库

凸优化课程笔记.pdf

相关推荐

课程资源

热门标签

最新资料