高层建筑脉动风荷载模拟.pdf-资料库

高层建筑顺风向脉动风荷载模拟 http://www.paper.edu.cn 郭炜，沈少波武汉理工大学土木工程与建筑学院，武汉（430070） Email: Whlggw@163.com 摘要：传统的结构设计中常将风荷载用静力荷载等效，这忽略了风荷载的动力特性。本文分析了风荷载的基本性质，给出了高层建筑竖向相关的脉动风荷载的模拟方法。M.Shinozuka 方法得到的脉动风荷载样本的统计特征值能较好的符合理论值，系统阐述了这种方法的分析过程，其中涉及到脉动风荷载功率谱的计算。采用 MATLAB 可以方便有效的进行编程，其中的矩阵函数能够容易的实现 Cholesky 分解以及随机数的求取等。在此基础上，以武汉世茂锦绣长江 A2 地块 1 号楼 1-3 单元高层为背景给出了计算实例。关键词：风荷载模拟；谐波叠加法；风速功率谱；风压功率谱；时程样本功率中图分类号：TU3 1. 引言近年来,随着生产生活的需要,大型结构日益受到人们的青睐,大跨度桥梁跨度已从 20 世纪初的 500m 到世纪末已逼近 2000m;大跨度空间结构跨度也已超过了 200m;高层建筑方面, 台北 101 大楼达到了 508m。随着新技术、新材料、新工艺、新型式、新设计方法的应用, 工程结构将日趋大型化、复杂化,这也必然使结构更轻更柔,对于风荷载将更加敏感。对于这些大跨、高层、高耸结构,风荷载往往起主要甚至决定作用,因此对于这些结构在风荷载作用下的响应研究越来越受到科研工作者的重视。在风的时程曲线中，一般包含两种成分:一种是长周期部分，其值常在 10 分钟以上;另一种是短周期分，常仅有几秒种左右。由于风的长周期远远大于一般结构的自振周期，其对结构的作用相当于静力作用脉动风是由于风的不规则性引起的，它的强度是随时间按随机规律变化的，由于它的周期较短，因而其作用性质是动力的，会引起结构的振动。时域内脉动风荷载的分析，就是用随机过程模拟的方法得到脉动风速时程或脉动风压时程。目前，随机过程的模拟方法[1]可以分为自回归滑动平均法[7]和谐波合成法两类，本文采用谐波合成法模拟风荷载。谐波合成法是将随机过程或场表示成大量具有随机相位的正弦或余弦之和。这种表示法最早是由 Rice 提出的。Shinzuka 在 70 年代初首先用这种方法模拟了随机过程和场。该模型适用于模拟具有任意形状密度的平稳随机过程，而且所得到的结果的样本是连续的。 2. 脉动风荷载功率谱 2.1 脉动风速谱在风的顺风向时程曲线中，一般包含平均风和脉动风两部分。平均风是在给定的时间间隔内，把风对建筑物作用力的速度、方向以及其它物理量都看成不随时间而改变的量，考虑到风的长周期远远大于一般结构的自振周期，因而其作用性质相当于静力；脉动风是由于风的不规则性引起的，它的强度是随时间按随机规律变化的，由于周期较短，因而其作用性质是动力的，将引起结构的振动。作用于结构上任意高度处的风速 v(z,t)可以表示为平均风速 [2]v(z)和脉动风速 v(z,t)之和。风的模拟主要是针对脉动风而言。 (1) 现在在风工程界广泛承认的顺风向水平脉动风速谱为 Davenport 谱[2]，也是我国规范所 f v z t ( , ) = v z ( ) + v z t ( , ) - 1 -

采用的风速谱。它假设紊流尺度沿高度不变，谱密度函数为 http://www.paper.edu.cn S v ( ) ω = 4 Kv 2 (10) x = 其中， 600 / K 为反映地面粗糙度的系数。 vω π (10) ， 0ω≥ 为频率（rad/s）, x (1 + ω v (10) ) 2 4/3 (2) 2 x 为离地面10m 高处的平均风速（m/s）； 2.2 脉动风压的规格化功率谱根据空气动力学研究结果，近地风可按无压缩流分析，风速与风压的基本关系为 w vρ= 1 2 2 (3) 其中，ρ 为空气密度。作用于结构上任意高度处的风压 ( , ) 脉动风压 ( , ) fw z t 之和。 w z t 可以表示为平均风压 ( )w z 和 w z t ( , ) = w z w z t ( , ) ( ) + f (4) 由风速与风压的关系式(3)可得到脉动风压方差与脉动风速方差的关系为 2 σ wf z ( ) = 4 w z ( ) v z ( ) 2 σ vf z ( ) (5) 又由零均值的高斯平稳随机过程的性质有 ∫ ∫ 0 可得脉动风压功率谱与脉动风速谱之间的关系为 2 σ wf 2 σ vf z ( ) z ( ) 0 ∞ = = ∞ S z ( , w ω ω d ) S z ( , v ω ω d ) (6) S z ( , w ) ω = 4 w z ( ) v z ( ) S z ( , v ) ω (7) 将 Davenport 谱(2)代入(7)得 S z ( , w ω ) 16 = K w z ( ) 2 v (10) 2 v z ( ) x + 2 x (1 ω ) 2 4/3 (8) 若将脉动风压表示成位置与时间的函数 w z t ( , ) f = w z f ( ) f f zϖ 应用统计值即 ( ) 因为脉动风压是随机荷载，所以 ( ) S z ( , w 2 ω σ wf z S ( ) = ) f t ( ) wf zσ 代入，则有 ( ) ω (9) (10) 将(6)和(8)代入(10)可得 2.3 脉动风的空间相关性 S f ( ) ω = x 2 2 x 3 (1 + ω ) 2 4/3 (11) 阵风的特性除考虑其自相关性外，还需要考虑其空间相关性。强风观测表明，各点风速、风向并不是完全同步的，甚至可能完全无关。空间相关性主要包括侧向左右相关和竖向上下 - 2 -

相关，必要时还应包括前后相关。有关脉动风的空间相关性研究较多，计算公式也较多。为了实用简便，一般采用 Shiotani 在试验中获得的只与两点距离有关的简单表达式计算其相关系数[3]公式为 http://www.paper.edu.cn ρ ij ( ) = exp( − j z i − z j / L z ) (12) z z , i z z , i 其中， zL = 和 60 ( ρ ij (13) xL = 是根据试验统计分析得出的经验值。为了分析问题方便，相当多 50 j j = − exp( − ) / L x ) x i x 的工程问题仅考虑了脉动风的竖向上下相关，而忽略了其侧向左右相关。 2.4 脉动风荷载功率谱对于离散化为 q 个自由度的结构体系，脉动风荷载离散化为每个集中质点上的离散化的水平风荷载 ( ) iF t ，且有 F t ( ) i ( f iA 为结构第 i 个集中质点上的等效受风面积。 w z t A w z A f i , ) = = ( ) f i i i t ( ) = σ wf ( z A f i i ) t ( ) (14) wf zσ 与保证系数 µ 的乘积（µ 一在实际应用中，设计脉动风压取为脉动风压均方差 ( ) f zµ 般取 2.0-2.5）。设计脉动风压与平均风压之比为脉动系数 ( ) µ = z ( ) f z ( ) µσ wf w z ( ) (15) 则有 σ wf z ( ) = µ f z w z ( ) ( ) µ (16) 因脉动风压随高度变化不大，而平均风压随高度而增大，故脉动系数随高度增加而减小，根据国内实测数据，并参考国外资料取其中，α 为地面粗糙度系数。 µ f z ( ) 0.5 35 = × 1.8( α − 0.16) z ( 10 α − ) (17) 为了既反映各种因素对结构平均风荷载的影响，又便于工程应用，我国规范规定计算平均风压的公式为 w z ( ) = µµ µ z z ( ) r s 其中， rµ 为重现期调整系数； ( ) 建筑物所在地区的基本风压。 s zµ 为风荷载体型系数； ( ) z w ( ) (18) 0 z zµ 为风压高度变化系数； 0ω 为 µ = z ( ) z ( z H T 2 α ) × 0.32 35 ≈ 3.12( z H T 2 α ) (19) 其中， TH 为梯度风高度。结合(16)和(18)，(14)可写为 F t ( ) i = 1 µ µµ µ µ z r s f i i ( z ( z ) ) ( z w A f i i ) 0 t ( ) (20) - 3 -

记 F i = 则有 1 µ µµ µ µ z r s f i i ( z ( z ) ) http://www.paper.edu.cn ( z w A i i ) 0 F t ( ) i = F f i t ( ) (21) 所以脉动风荷载的自谱密度函数为 S Fi 互谱密度为 F Sω ( 2 = ) i ( ) ω f (22) ⋅ Fi ) ) S S S = FiFj ( ω ρ ij ( ω ω ρ ij F F S ⋅ ⋅ ⋅ i f pS ω 为根据以上结果，可得到结构风荷载功率谱密度函数[4]矩阵 ( ( ) ω (24) f 其中， pS 为 q q× 阶常量矩阵，它的 i 行 j 列元素为 ij F F ρ ⋅ i (23) S Sω ( p ⋅ 。 ( ) ω j ) = = S ( ) ) Fj p j 3. 风荷载模拟方法本论文采用 M.Shinozuka 方法[8]模拟风荷载。风荷载功率谱密度函数矩阵 ( ) 数矩阵，也可为实数矩阵，这要视相关系数的形式而定。不失一般性，设 ( 阵，其对角元素为实数，非对角元素为复数。由 Cholesky 分解法 pS ω 可为复 pS ω 为复数矩 ) pS H ( TH ω 为 ( )H ω 为下三角矩阵； ( = ) 其中， ( )H ω 的共轭转置矩阵。 ( ) ω ω ω H ) ) ( ⋅ T (25) 根据 M.Shinozuka 方法，作用在结构第 i 个质点处的脉动风荷载[5]可表示为 F t ( ) i = i N ∑∑ j 1 = k 1 = H ( ω k ) 2 ij ω ω θ ω φ ∆ jk cos[ + + ( ) ij t k k ] (26) 其中，N 是风谱在频率内的划分数，是一个充分大的正整数； ω∆ 为频率增量 = ω ω ω l u − N (27) lω和 uω 分别为风谱频率下限和上限，并且要求 uω 满足关系式 u ω ω ω ε ) (1 = − d ) S ( f ∫ 0 ∞ ∫ 0 S f ( ω ω d ) (28) 其中，ε<<1（如 0.01 或者 0.001）。选取的截至频率越高，式(26)代表的风样本就越逼近风谱的总能量。 ω ω= l 1 2 )kH ω 的第(i,j)个元素； ( ij + − k ( k k ij ( ) H ω 为 ( 间的相位角 ) ( k 1,2, = L (29) N ) H ω 为 ( ij H ω 的模； ( kθ ω 为两个不同作用点之 ij ) ) ) k k θ ω k ij ( ) = art tan ⎡ ⎢ ⎢ ⎣ Im ( ω ij k ( Re ω k H H ij ) ) ⎤ ⎥ ⎥ ⎦ (30) 其中，Im 和 Re 分别表示虚部和实部； jkφ 是在[0,2π]上均匀分布的随机数。 - 4 -

根据采样定理，为避免模拟样本的重叠，时间间隔 t∆ 必须满足 / 对于论文所采用的相关系数(12)，则(26)简化为 t π ω ∆ ≤ u (31) http://www.paper.edu.cn F t ( ) i = 4. 脉动风荷载模拟算例 i N ∑∑ j 1 = k 1 = H ij ( ω k ) 2 ω ω φ ∆ jk cos[ + t k ] (32) 武汉世茂锦绣长江 1-3 单元高层建筑总高度为 187.6m，采用上述风荷载模拟方法，模拟出符合高层特性和风荷载随机性、高斯平稳性的脉动风荷载。结构在每个楼面处确定一个质点，共 57 个质点，只考虑竖向相关性。采用 Davenport 谱，模拟中各种参数取值为： kN m ；梯度风高度： TH ＝350m；保证系数：µ＝2.25；重现期调整系数： s zµ ＝1.3；频率划分数：N＝1024；频率下限： lω＝0.01（rad/s）；基本风压： rµ ＝1.1；风荷载体型系数： ( ) 频率上限 uω ＝ 2π（rad/s）； t∆ ＝0.1s。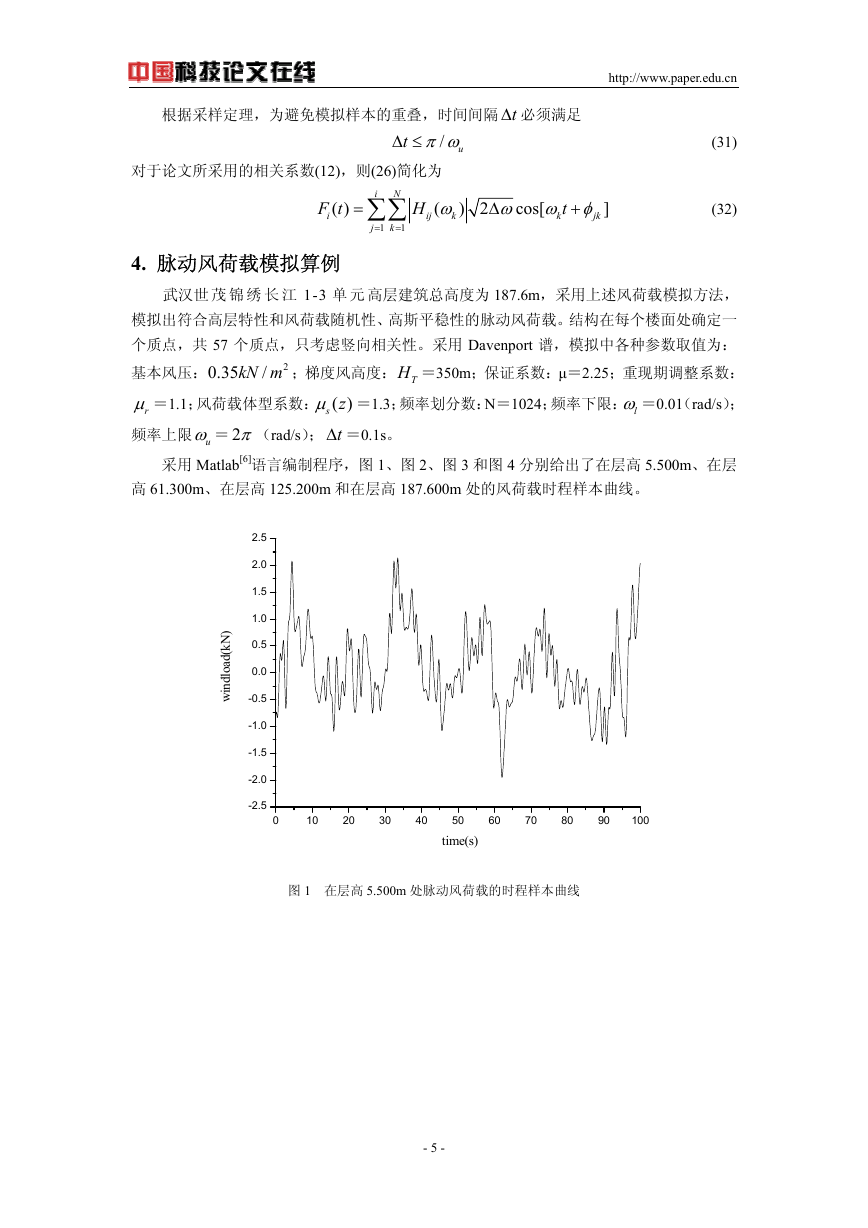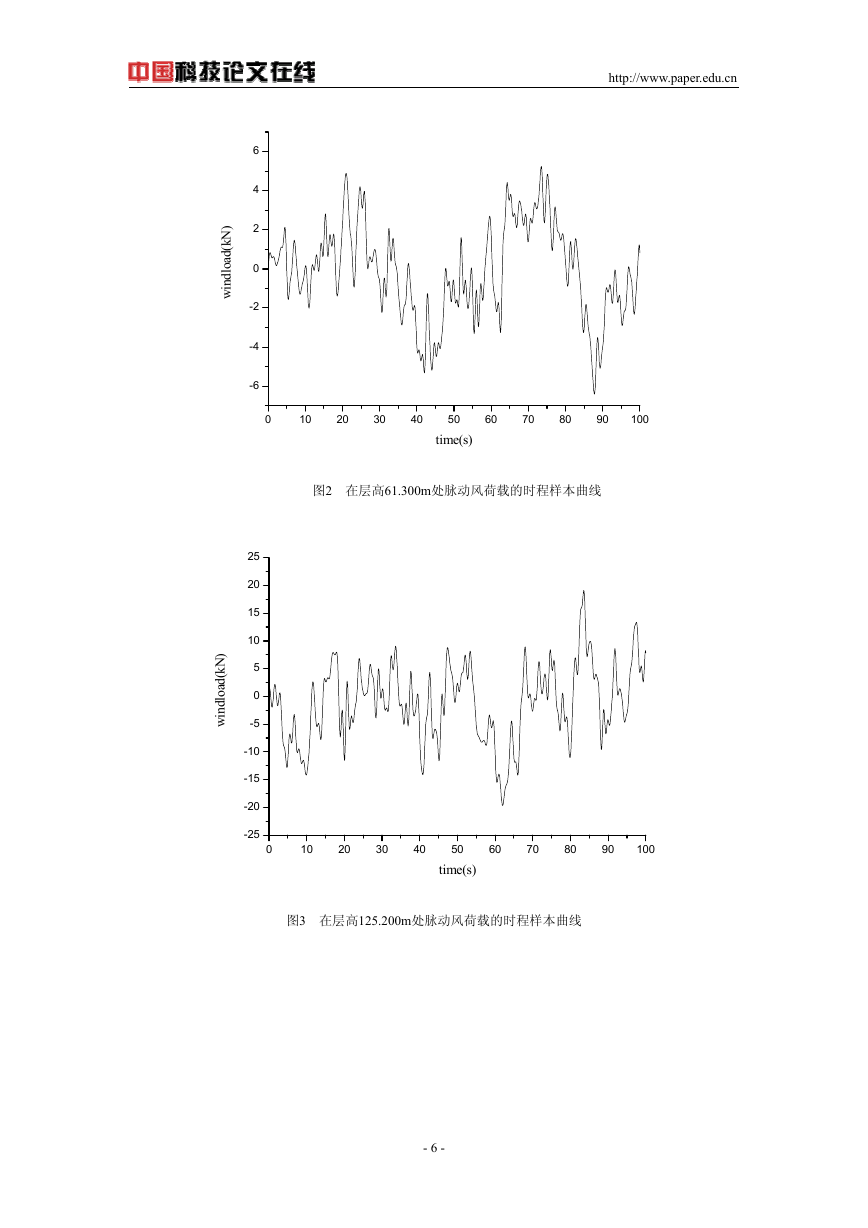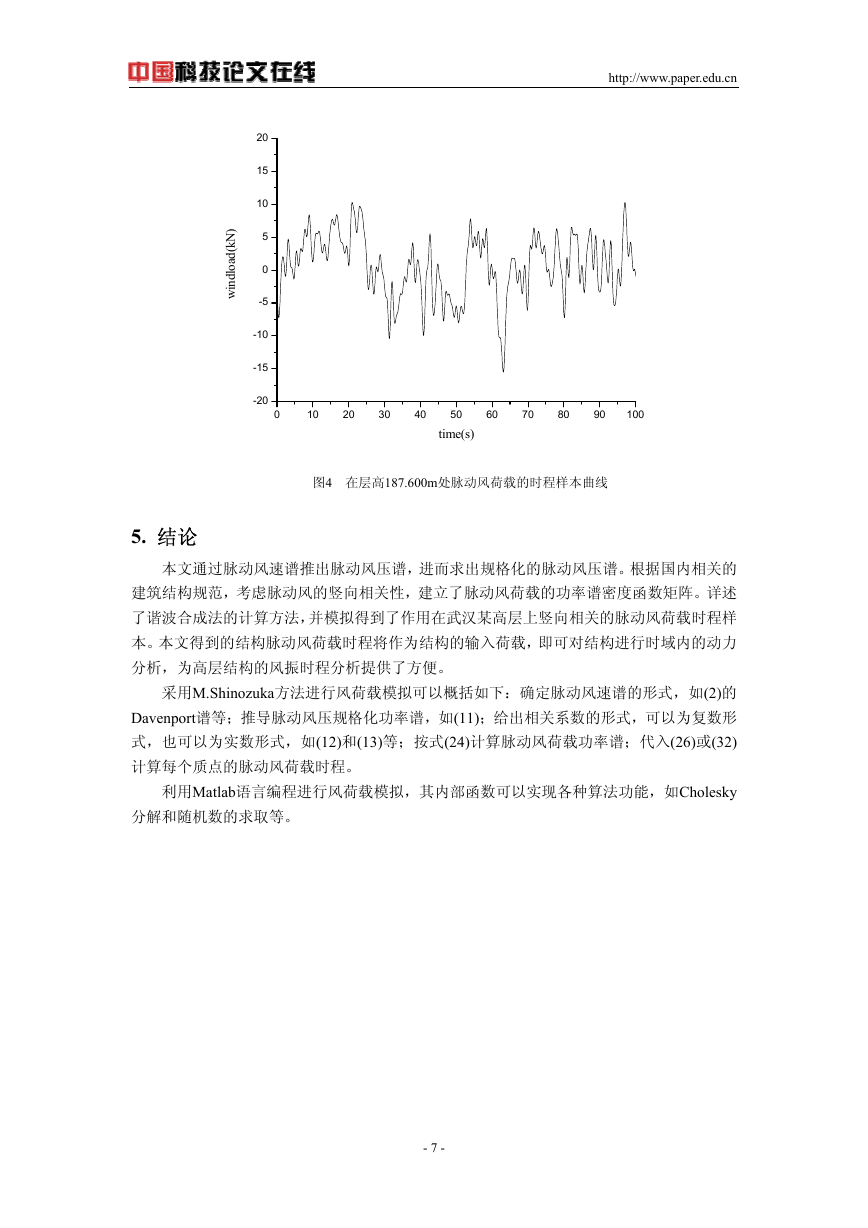 0.35 / 2 采用 Matlab[6]语言编制程序，图 1、图 2、图 3 和图 4 分别给出了在层高 5.500m、在层高 61.300m、在层高 125.200m 和在层高 187.600m 处的风荷载时程样本曲线。 ) N k ( d a o l d n i w 2.5 2.0 1.5 1.0 0.5 0.0 -0.5 -1.0 -1.5 -2.0 -2.5 0 10 20 30 40 50 60 70 80 90 100 time(s) 图 1 在层高 5.500m 处脉动风荷载的时程样本曲线 - 5 -

http://www.paper.edu.cn 0 10 20 30 40 50 60 70 80 90 100 time(s) 图2 在层高61.300m处脉动风荷载的时程样本曲线 ) N k ( d a o l d n i w ) N k ( d a o l d n i w 6 4 2 0 -2 -4 -6 25 20 15 10 5 0 -5 -10 -15 -20 -25 0 10 20 30 40 50 60 70 80 90 100 time(s) 图3 在层高125.200m处脉动风荷载的时程样本曲线 - 6 -

http://www.paper.edu.cn ) N k ( d a o l d n i w 20 15 10 5 0 -5 -10 -15 -20 0 10 20 30 40 50 60 70 80 90 100 time(s) 图4 在层高187.600m处脉动风荷载的时程样本曲线 5. 结论本文通过脉动风速谱推出脉动风压谱，进而求出规格化的脉动风压谱。根据国内相关的建筑结构规范，考虑脉动风的竖向相关性，建立了脉动风荷载的功率谱密度函数矩阵。详述了谐波合成法的计算方法，并模拟得到了作用在武汉某高层上竖向相关的脉动风荷载时程样本。本文得到的结构脉动风荷载时程将作为结构的输入荷载，即可对结构进行时域内的动力分析，为高层结构的风振时程分析提供了方便。采用M.Shinozuka方法进行风荷载模拟可以概括如下：确定脉动风速谱的形式，如(2)的 Davenport谱等；推导脉动风压规格化功率谱，如(11)；给出相关系数的形式，可以为复数形式，也可以为实数形式，如(12)和(13)等；按式(24)计算脉动风荷载功率谱；代入(26)或(32) 计算每个质点的脉动风荷载时程。利用Matlab语言编程进行风荷载模拟，其内部函数可以实现各种算法功能，如Cholesky 分解和随机数的求取等。 - 7 -

http://www.paper.edu.cn 参考文献 [1] 刘锡良，周颖，风荷载的几种模拟方法[J].工业建筑，2005. [2] 张相庭，结构风工程[M]。北京:中国建筑工业出版社，2006. [3] 张相庭，结构风压与风振计算[M].上海:同济大学出版社，1985. [4] 王之宏，风荷载的模拟研究[J].建筑结构，1994，15(1). [5] 张顺宝，结构脉动风荷载研究[J]。工程力学，2002 年增刊. [6] 张志涌.精通 MATLAB6.5 版[M].北京:北京航空航天大学出版社,2005. [7] J.S.Owen，et al．The application of auto-regressive time series modeling for the time-frequency analysis of civil engineering structures[J].Engineering Structures,2001,23:521-536． [8]M.Shinozuka,G.Deodatis.Simulation of stochastic process by spectral representation[J].Applied Mechanics Review,1994,44:191-203． Slmulation of Fluctuation Wind Load on High-rise Buildings Guo Wei, Shen Shaobo School of Civil Engineering and Architecture, Wuhan (430070） Abstract In the traditional structure design，wind load usually be equal to static load，which neglect the dynamical characteristic of fluctuating wind load. Base on the analysis of the essential character of fluctuating wind load，the method is given to simulate the fluctuating wind load of high-rise building. The sample’s statistical characteristics of impulsive wind load can well accord with the theoretical value by M. Shinozuka method, Relating to the deduction of wind pressure uniform spectrum and calculation of wind load spectrum, analytical progress of M. Shinozuka method is systemically discussed. The program can be realized by MATLAB conveniently and effectively, in which Cholesky decomposition and random numbers can be easily acquired. Then，An example about high-rise building is given. Keywords: wind load simulation; spectral representation method; wind speed spectrum; wind pressure spectrum; time histories sample - 8 -

资料库

高层建筑脉动风荷载模拟.pdf

相关推荐

开发技术

热门标签

最新资料