数字信号处理C语言各种算法实现.pdf-资料库

1.[数字信号处理] FIR 滤波器基础 2.[数字信号处理]使用窗函数设计 FIR 滤波器 3.[数字信号处理]单位冲击响应的频响与 FIR 的实现代码（C 语言） 4.[数字信号处理]相位特性解卷绕 5.[数字信号处理]IIR 滤波器基础 6.[数字信号处理]IIR 滤波器的间接设计 7.[数字信号处理]IIR 滤波器的直接设计 [数字信号处理] FIR 滤波器基础对于一个滤波器而言，其单位冲击响应是有限区间的数列的话，这个滤波器是 FIR 滤波器。反之，其单位冲击响应是无限区间的数列的话，这个滤波器是 IIR 滤波器。下面使用线性差分方程式，在时域内，解释一下 FIR 与 IIR 数字滤波器。使用单位脉冲响应和其输入信号进行卷积运算，可得到下式将其改写为递归的方式，则上式是 1 次差分方程式，而对于 N 次数字滤波器的输入输出关系，表示为 N 次差分方程式，如下所示。由上式看，输出 y(n) 需要自己的历史值，也就是，含有反馈。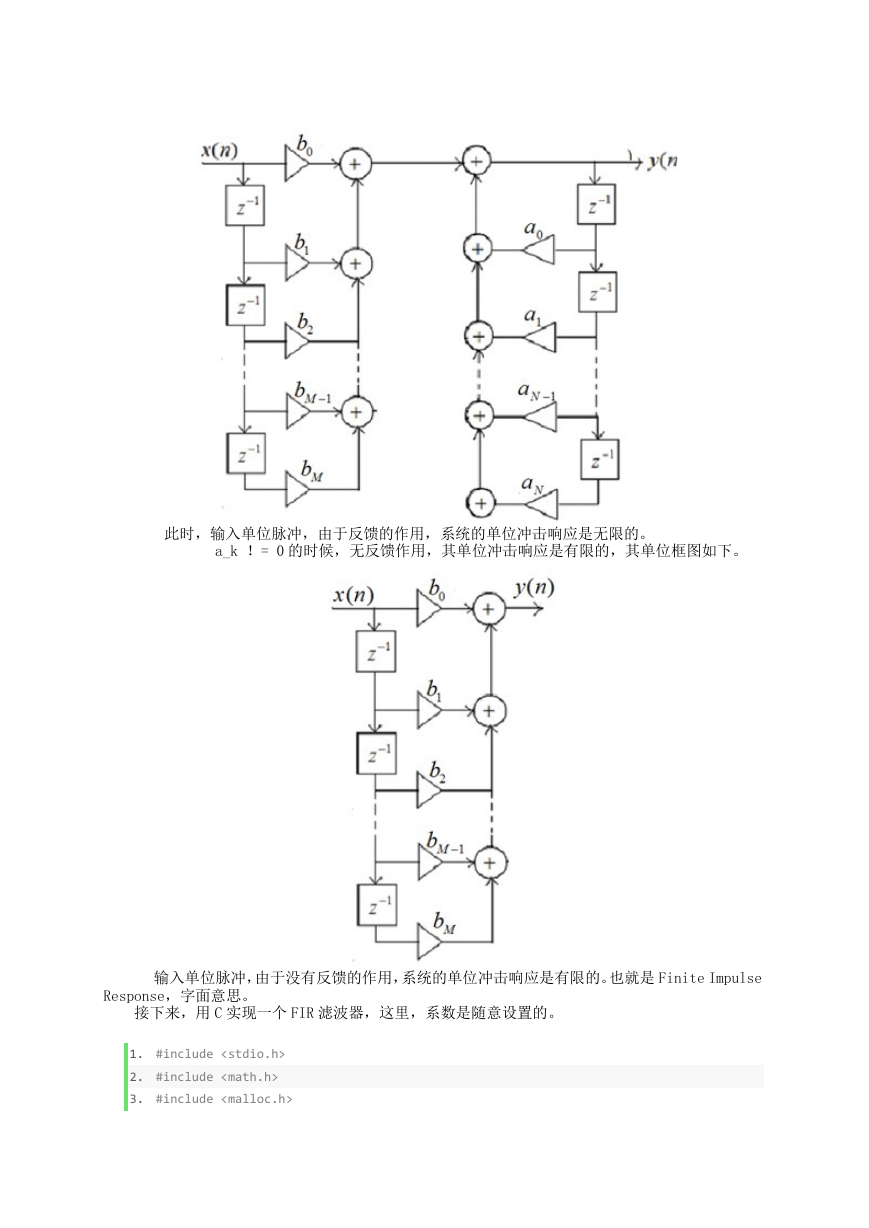 a_k = 0 的时候，反馈有作用，其系统框图如下。

此时，输入单位脉冲，由于反馈的作用，系统的单位冲击响应是无限的。 a_k ！= 0 的时候，无反馈作用，其单位冲击响应是有限的，其单位框图如下。输入单位脉冲，由于没有反馈的作用，系统的单位冲击响应是有限的。也就是 Finite Impulse Response，字面意思。接下来，用 C 实现一个 FIR 滤波器，这里，系数是随意设置的。 1. #include 2. #include 3. #include

4. #include 5. 6. 7. double Real_Time_FIR_Filter(double *b, 8. int b_Lenth, 9. double *Input_Data) 10. { 11. int Count; 12. double Output_Data = 0; 13. 14. Input_Data += b_Lenth - 1; 15. 16. for(Count = 0; Count < b_Lenth ;Count++) 17. { 18. Output_Data += (*(b + Count)) * 19. (*(Input_Data - Count)); 20. } 21. 22. return (double)Output_Data; 23. } 24. 25. void Save_Input_Date (double Scand, 26. int Depth, 27. double *Input_Data) 28. { 29. int Count; 30. 31. for(Count = 0 ; Count < Depth-1 ; Count++) 32. { 33. *(Input_Data + Count) = *(Input_Data + Count + 1); 34. } 35. 36. *(Input_Data + Depth-1) = Scand; 37. } 38. 39. 40. int main(void) 41. { 42. double b[] = {0.5 , -0.5 , 1}; 43. double Scand_Data = 0; 44. char Command = 0; 45. 46. int b_Lenth = (sizeof(b)/sizeof(double));

47. int Count = 0; 48. 49. double Input_Data[sizeof(b)/sizeof(double)] = {0}; 50. double Output_Data = 0; 51. 52. /*--------------------display----------------------------*/ 53. printf(" b(k) : "); 54. for(Count = 0; Count < b_Lenth ;Count++) 55. { 56. printf("%f " , b[Count]); 57. } 58. printf("\n"); 59. /*-----------------------------------------------------*/ 60. 61. Count = 0; 62. while(1) 63. { 64. if(Count == 0) printf("The Input : "); 65. else printf("The Next Input : "); 66. 67. scanf("%lf",&Scand_Data); 68. printf("Input x(%d) : %lf ",Count,Scand_Data); 69. 70. Save_Input_Date (Scand_Data, 71. b_Lenth, 72. Input_Data); 73. 74. Output_Data = Real_Time_FIR_Filter(b, 75. b_Lenth, 76. Input_Data); 77. 78. printf("Output y(%d) : %lf \n",Count,Output_Data); 79. 80. scanf("%c",&Command); 81. if(Command == 27) break; //ESC 82. 83. Count++; 84. } 85. 86. printf("\n"); 87. 88. return (int)0; 89. }

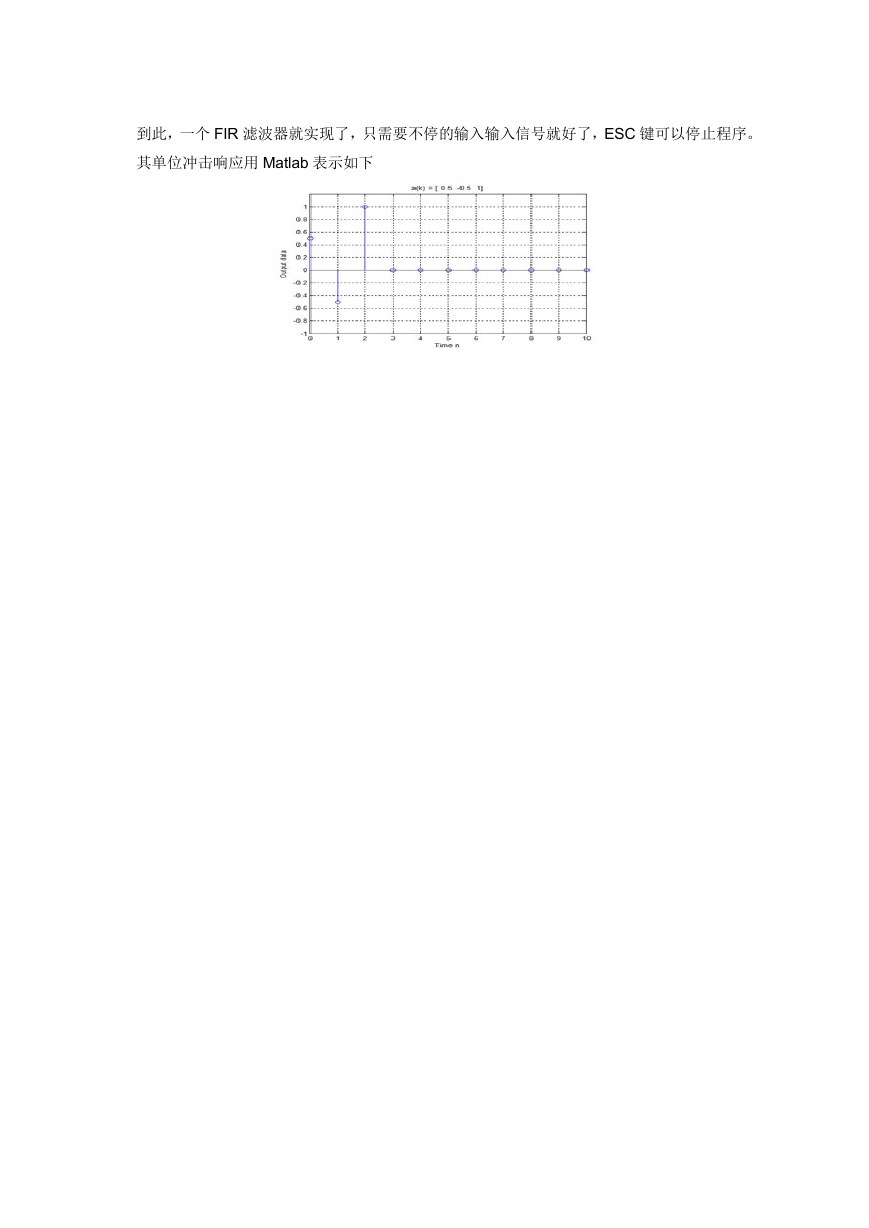
到此，一个 FIR 滤波器就实现了，只需要不停的输入输入信号就好了，ESC 键可以停止程序。其单位冲击响应用 Matlab 表示如下

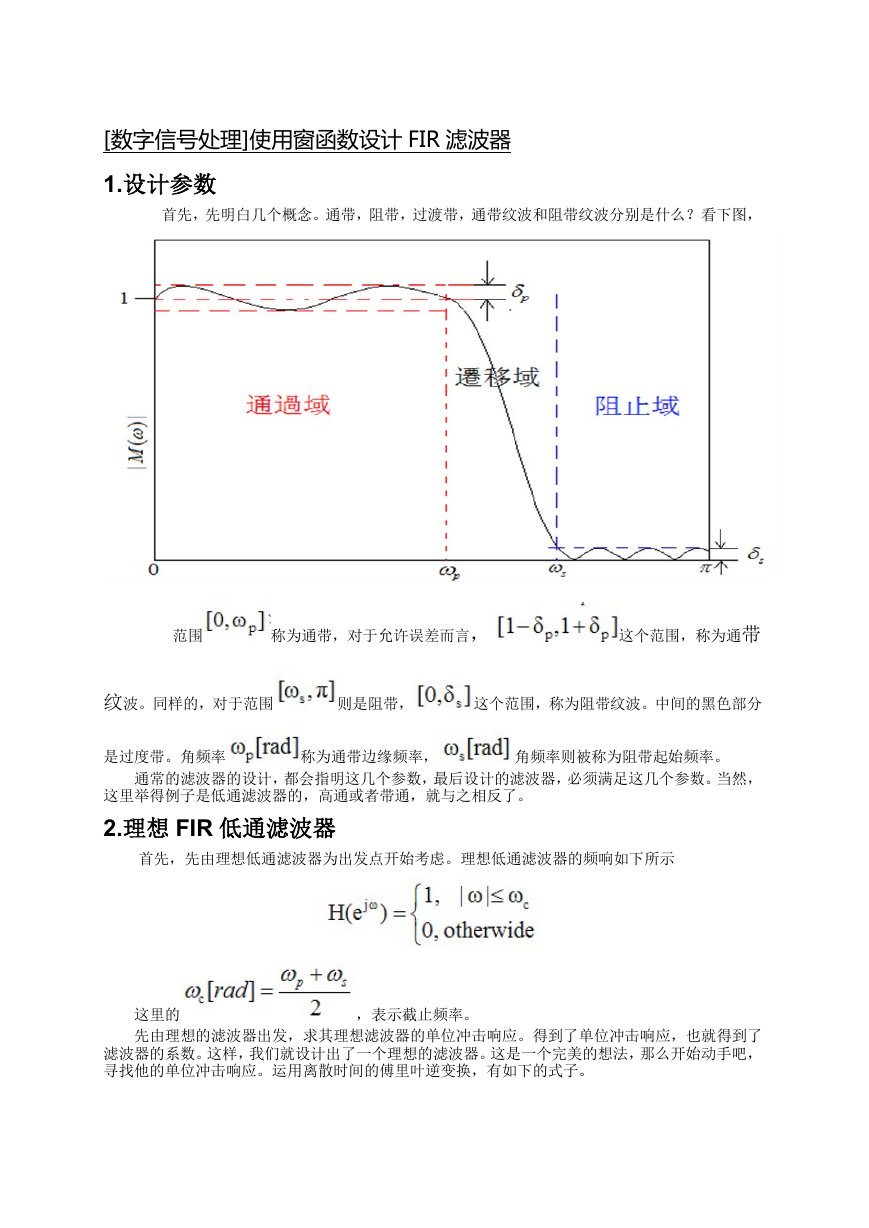
[数字信号处理]使用窗函数设计 FIR 滤波器 1.设计参数首先，先明白几个概念。通带，阻带，过渡带，通带纹波和阻带纹波分别是什么？看下图，范围称为通带，对于允许误差而言，这个范围，称为通带纹波。同样的，对于范围则是阻带，这个范围，称为阻带纹波。中间的黑色部分是过度带。角频率称为通带边缘频率，角频率则被称为阻带起始频率。通常的滤波器的设计，都会指明这几个参数，最后设计的滤波器，必须满足这几个参数。当然，这里举得例子是低通滤波器的，高通或者带通，就与之相反了。 2.理想 FIR 低通滤波器首先，先由理想低通滤波器为出发点开始考虑。理想低通滤波器的频响如下所示这里的先由理想的滤波器出发，求其理想滤波器的单位冲击响应。得到了单位冲击响应，也就得到了滤波器的系数。这样，我们就设计出了一个理想的滤波器。这是一个完美的想法，那么开始动手吧，寻找他的单位冲击响应。运用离散时间的傅里叶逆变换，有如下的式子。，表示截止频率。

由此，我们得到了一个单位冲击响应的表达式（sinc 是辛格函数），到这我们就可以设计出一个理想的滤波器了吗？好吧，让我们再确认一遍。第一，这个式子是离散的。对于单位冲击响应，本来就应该是离散的，没有错，很好，我们距离理想滤波器又近了一步。第二，这个式子所求出的单位冲击响应的个数，很不幸！个数是无限的。到这里，我们基本可以确定了，理想滤波器是实现不了的。虽然理想滤波器是实现不了的，但是我们可以退一步，从无限的理想滤波器的单位冲击响应中，在选择一部分冲击响应，构成一个不太理想的，但又达到一定标准的滤波器。我们只能“将就”着使用这个不太理想的滤波器，那么接下来还有一个问题，我们要如何从无限的数列中选择出有限的一部分，从而达到我们的设计要求。 3.窗函数首先，我们先考虑最简单的情况。对于理想单位冲击响应而言，其形状大概和一个高斯分布很像（当然，只是很像，n=0 时候，单位冲击响应的值最大，由两边慢慢减少。当然，可能也出现负值。）！所以，我们为了能使得滤波器的性能接近理想滤波器，那么，我们选择其最主要的部分，也就是，值较大的部分。其余部分则放弃。根据之前的叙述，我们可以使用如下式子表示。这个式子确实可以帮助我们选择一部分有限的数列。而这个式子，被称为矩形窗。可以看出，Ｎ越大，性能越街进理想滤波器。这里Ｎ称为窗函数的长度。这就是我们选定的窗口，然后我们把窗口函数加上，也就是加窗！其实也就一个乘法，如下所示。这样，也就完成了一个加窗。但是，在实际的实践过程中，很少用矩形窗的。其原因是，矩形窗的阻带衰减不够，仅仅只有 21[dB]。于是，各种各样的窗口就被提出了。各有各的特点，在我们所学的初步的设计中，我们就仅仅看阻带衰减就够了。各种窗函数的性能如下。 ================================================ 窗函数过渡带大小阻带衰减 ================================================

矩形窗 1.8π/N 21[dB] 汉宁窗 6.2π/N 44[dB] 汉明窗 6.6π/N 53[dB] 布莱克曼窗 11π/N 74[dB] 4.用窗函数实现一个 FIR 滤波器以上说了很多有关于窗函数的原理，现在来整理一下设计的步骤。 1.根据设计的规格，参数要求，我们选择一个适合的窗函数。这里主要我们还是看阻带衰减，阻带衰减要大于给定的值。一般，若没有给定阻带衰减，我们则需要通过通带纹波和阻带纹波去求，如下。 2.根据要求的通带边缘频率和阻带起始频率，计算过度区的大小，从而计算出窗函数的长度。 3.最后，根据窗函数和理想滤波器的单位冲击响应，计算出我们所需要的滤波器的单位冲击响应。现在，我们来实战一下，假设我们需要设计如下滤波器。规格中，没有给定阻带衰减，我们只能自己计算。这里，阻带衰减为 40.8[dB]，我们选择的窗的阻带衰减不能比这个小，这里其实汉宁窗就可以做到。但我还是选择用汉明窗去做。然后，计算窗长度。

资料库

数字信号处理C语言各种算法实现.pdf

相关推荐

后端

热门标签

最新资料