惯性传感器和磁力计的确定性误差建模和校准的改进.pdf-资料库

Sensors and Actuators A 247 (2016) 522–538 Contents lists available at ScienceDirect Sensors and Actuators A: Physical j o u r n a l h o m e p a g e : w w w . e l s e v i e r . c o m / l o c a t e / s n a Improvements in deterministic error modeling and calibration of inertial sensors and magnetometers Gorkem Secer, Billur Barshan∗ Department of Electrical and Electronics Engineering, Bilkent University, Bilkent, TR-06800 Ankara, Turkey a r t i c l e i n f o a b s t r a c t We consider the deterministic modeling, calibration, and model parameter estimation of two commonly employed inertial measurement units based on real test data acquired from a ﬂight motion simulator. Each unit comprises three tri-axial devices: an accelerometer, a gyroscope, and a magnetometer. We perform the deterministic error modeling and calibration of accelerometers based on an improved mea- surement model, and the technique we propose for gyroscopes lowers costs by eliminating the need for additional sensors and relaxing the test bed requirement. We present an extended measurement model for magnetometers that reduces calibration errors by modeling orientation-dependent hard-iron errors in a gimbaled angular position-control machine. While we employ the model-based Levenberg- Marquardt optimization algorithm for the parameter estimation of accelerometers and magnetometers, we use a model-free evolutionary optimization algorithm (particle swarm optimization) for estimating the calibration parameters of gyroscopes. Errors are considerably reduced as a result of proper modeling and calibration. © 2016 Elsevier B.V. All rights reserved. Article history: Received 29 January 2016 Received in revised form 14 June 2016 Accepted 20 June 2016 Available online 1 July 2016 Keywords: Inertial sensors Accelerometer Gyroscope Magnetometer Deterministic error modeling Measurement model In-ﬁeld calibration Model parameter estimation Ellipsoid parameter estimation Levenberg-Marquardt algorithm Particle swarm optimization 1. Introduction Inertial sensors were mainly only used in aeronautics and maritime applications until the nineties because of the high cost associated with the high-accuracy requirements. With developments in micro-electro-mechanical systems (MEMS), the availability of small, lower-cost, medium-performance inertial sen- sors has opened up new possibilities for their use, such as the recognition of daily activities [1], physical therapy and home-based rehabilitation [2], biomechanics [3], detecting and classifying falls [4,5], shock and vibration analysis, navigation of unmanned vehi- cles [6–8], and state estimation and dynamic modeling of legged robots [9]. Inertial measurement units (IMUs) typically contain gyroscopes and accelerometers, sometimes used in conjunction with mag- netometers. Each device can be sensitive around a single axis or multiple axes (usually two or three). An accelerometer detects spe- ciﬁc force, which is proportionate to the acceleration of the sensor ∗ Corresponding author. E-mail addresses: gorkem.secer@ceng.metu.edu.tr (G. Secer), billur@ee.bilkent.edu.tr (B. Barshan). http://dx.doi.org/10.1016/j.sna.2016.06.024 0924-4247/© 2016 Elsevier B.V. All rights reserved. relative to an inertial reference frame along its axis of sensitivity. A gyroscope senses the angular rate about an axis of sensitivity with respect to an inertial reference frame [10,11]. Magnetometers measure the magnetic ﬁeld strength at a given location superposed with the Earth’s magnetic ﬁeld [12]. They are used in a wide range of disciplines, from archaeology [13] to vehicle navigation and control [14]. Consumer-grade inertial sensors have attracted much interest recently because of their decreasing cost due to developments in MEMS technology [15]. Measurements by inertial sensors often deviate from the ground truth since the devices suffer from various error types, which can be constant or time varying. The rate output of accelerometers and gyroscopes needs to be integrated twice or once to obtain the linear or angular position, respectively. Because of the integration process, even very small errors at the output accu- mulate very rapidly and the position error becomes considerably large in a few seconds and starts drifting in time (i.e., proportionate with the time cube for the linear and the time square for the angu- lar position) [16]. This effect is exacerbated for low-grade sensors. Consumer-grade inertial sensors can be used for longer periods of time on their own if modeled and calibrated properly, but may need to be corrected from time to time by an external aid that provides an absolute reference for the ground truth [17,18]. Thus, to improve

G. Secer, B. Barshan / Sensors and Actuators A 247 (2016) 522–538 523 Fig. 1. The two sensor units used in this study: (a) MicroStrain 3DM-GX2 [22] and (b) Xsens MTx [23]. the accuracy of linear and angular position estimates, it is necessary to characterize and model the errors at the sensor output precisely. The same holds for magnetometers that suffer from various error types. Most previous works have divided the calibration problem into two distinct parts (deterministic and stochastic modeling) because of their different mathematical natures [10,19,20]. Here, we follow the same approach and focus on deterministic calibration only. Stochastic calibration is considered in a different study [21]. Working from their raw outputs, we consider the deterministic calibration of two widely used consumer-grade IMUs and compare their performances: MicroStrain’s 3DM-GX2 [22] and Xsens’ MTx [23], depicted in Fig. 1, with their technical speciﬁcations provided in the respective references. The units are small, light, and com- prised of three tri-axial devices: an accelerometer, a gyroscope, and a magnetometer. The main objective of this study is to effectively model and estimate the units’ deterministic calibration parame- ters so that both their stand-alone and aided performances can be improved. Motivated by insights gained from earlier work, we propose improved models and algorithmic ideas and implement them to improve the sensor calibration process. The main contributions of this article are threefold: • We propose an improvement to the traditional measurement model used in 1g tests for modeling the deterministic errors of accelerometers. The method’s effectiveness is shown through experiments, and the results are compared with those of the tra- ditional model. • We employ a low-cost calibration technique to estimate the error components associated with gyroscopes. Our technique is based on comparing the attitude of the IMU, calculated by integrating the gyroscope measurements, with the reference attitude pro- vided by a 3-DoF ﬂight motion simulator (FMS). In this way, we eliminate the need for any additional sensors to perform the cal- ibration, unlike previously used low-cost gyroscope calibration techniques. Another novel aspect of this work is that to esti- mate the model parameters that minimize the attitude error of gyroscopes, we use a global optimization algorithm [particle swarm optimization (PSO)] instead of gradient-based techniques, to avoid convergence to local minima. • We propose an extended sensor measurement model for mag- netometers that reduces calibration errors by modeling the orientation-dependent magnetic disturbances in gimbaled angu- lar position-control machines. We experimentally verify that incorporating in the model the relative motion between the magnetometer and the magnetic distortion sources in the envi- ronment enhances the calibration accuracy. The rest of this article is organized as follows: In Section 2, we ﬁrst develop individual deterministic sensor measurement models for each type of sensor and then propose a uniﬁed measurement model for all three sensor types. Section 3 describes the data acqui- sition experiments conducted for calibrating the sensors and brieﬂy reviews geometric and algebraic parameter estimation techniques. We then present our model parameter estimation results based on the acquired data and propose an extended measurement model for magnetometers. We compare the two units in terms of mea- surement quality based on the results of deterministic calibration. In Section 4, we summarize our contributions, make concluding remarks, and provide some directions for future research. In the appendices, we provide background information on the two opti- mization algorithms that we use for parameter estimation. 2. Sensor measurement models The general measurement model of the sensors evaluated in this (1) R3 × Rdim() → R3. The em, e, and n ∈ study is given by: em = h(e, ) + n where h(e, ) : R3 denote the measured sensor output, the true value of the excitation signal, and the additive stochastic measurement noise vector, respectively. The calibration parameter vector involved in this model needs to be estimated accurately in the scope of deterministic calibration. The following notation is used throughout: The measured sensor output em can be one of am, ωm, or Bm, for the accelerometer, gyro- scope, and magnetometer, respectively. The true excitation signal e can be one of a, ω, or B, which represent the true values of the speciﬁc acceleration, angular rate, and magnetic ﬁeld strength vec- tors. A vector u expressed with respect to a coordinate frame f is denoted by u f , and the rotational transformation matrix C f 2 , trans- u f 1 . Orthonormal forms a vector u f 1 from frame f1 to f2 as u f 2 = unit vectors of the x, y, and z axes of a given frame f are respectively denoted by i f ,j f , and k f . f 1 C f 2 f 1 To develop the deterministic measurement model of the sen- sors, we ﬁrst need to introduce several coordinate frames: • the north-east-down (NED) frame is shown in Fig. 2, with unit vectors i NED,j NED, and kNED, which point to the north, east, and down directions of the Earth, respectively. • the platform base frame (p) is an orthogonal frame ﬁxed to the base of the rotating platform onto which the sensor units are mounted, and does not move with the platform. • the sensor enclosure frame (q) corresponds to the orthogonal axes of the sensor’s mechanical casing. Due to manufacturing tolerances and packaging issues, in practice, this frame cannot

524 G. Secer, B. Barshan / Sensors and Actuators A 247 (2016) 522–538 illustrated in Fig. 4. This kinematic relation between frames r and s can be modeled by the non-orthogonalization (cross-axis sensitivity) matrix: 0 cos(˛1) 0 0 (3) ⎡ ⎣ 1 sin(˛1) = T s r ⎤ ⎦ cos(˛3) sin(˛2) sin(˛3) cos(˛2) sin(˛3) ∈ {1, 2, 3} T s r where ˛i, i are the sensor-to-sensor axis misalignment angles (Fig. 4). With this deﬁnition, a vector ur can be transformed from frame r to s as us = ur. = [ Sx According to a ﬁrst-order approximation at the sensor output [19], we introduce a diagonal scale factor error matrix S such that diag(S) Sz ]. A factor of (I + S) multiplies the true excita- × tion signal in the measurement model, where I is the 3 3 identity matrix, so that the output of each sensor axis is scaled by a different amount in general. Sy Fig. 2. The NED frame and the Earth’s frame of reference. Adopted from [67]. be perfectly aligned with the sensor’s actual sensitivity axes (s frame). This frame moves with the platform onto which the sen- sor units are attached. • the orthogonal sensor sensitivity frame (r) is the idealized, orthogonal sensor sensitivity frame. • the non-orthogonal sensor sensitivity frame (s) represents the set of the sensor’s actual sensitivity axes. Deviation from orthog- onality stems from manufacturing tolerances in general, and may affect navigation performance signiﬁcantly. When the input to the sensor is zero, the deviation of the output from the zero level is the bias error [6,19], denoted by b = [ bx by bz ]T in this study. The bias error may change with the sensor’s operating temperature and may drift in time. Since the experiments are conducted over short periods of time in this study, we assume a constant bias level. The deterministic error components and the transformation matrices introduced above are common to both inertial sensors and magnetometers. As shown in Fig. 3(a), for the platform that we use in the calibra- tion tests, the k unit vectors of the NED and p frames are coincident and their respectivei and j unit vectors lie on the horizontal plane, making an angle ˇ with each other. This is because the base of the facility where experiments are conducted was leveled with the North-East plane. Thus, the relationship between the two frames can be described by a rotational transformation Cp axis by ˇ: NED about the k ⎡ ⎣ cos ˇ − sin ˇ 0 = Cp NED ⎤ ⎦ sin ˇ 0 cos ˇ 0 1 0 (2) The matrix Cq p can be expressed mathematically by a sequence of basic rotations as Cq Rx()Ry()Rz( ), where , , and are the angles of rotation about the x, y, and z axes of the p frame, respectively. The basic rotation matrices are given by: p = cos − sin 0 0 0 ⎡ ⎣ 1 ⎡ ⎣ cos 0 ⎡ ⎣ cos 1 sin 0 0 = Rx() = Ry() = Rz( ) 0 sin cos − sin 0 cos ⎤ ⎦ ⎤ ⎦ ⎤ ⎦ sin 0 − sin cos 0 0 1 0 Similarly, the package misalignment matrix Cr q represents the = misalignment between frames q and r as Cr Rx(x)Ry(y)Rz(z), q where x, y, and z are the mounting misalignment angles about the x, y, and z axes of the q frame, respectively. The unit vectors of the r and s frames are such that ir and is are coincident,jr lies along the remaining perpendicular component of js after its projection onto ir, kr points in the same direction as the component of ks, perpendicular to the plane spanned byir andjr, as 2.1. Accelerometer measurement model rCr qCq p + S) T s ap + b + n After incorporating the error components described in the pre- vious section and the related transformations into the sensor measurement model in Eq. (1), we obtain the traditional ﬁrst-order measurement model of accelerometers [24–27]: am = (I (4) Here, am is the acceleration measured along the sensitivity axes of the accelerometer (the s frame), whereas the reference for the true value of the excitation signal ap is the p frame. We note that the composite matrix multiplying ap above represents a transfor- mation from the p to the s frame and corrects for the scale factor error. We propose the following improved measurement model: am = (I + S) T s rCr qCq pCp NED aNED + b + n (5) The main difference between the two models is that in the proposed model, the matrix Cp NED is included so that the reference for the true acceleration aNED is now the NED frame [28]. Accordingly, the h(e, ) for accelerometers is (I aNED + b. The com- posite matrix multiplying aNED here represents a transformation from the NED to the s frame and corrects for the scale factor error as well. + S) T s p Cp qCq rCr NED 2.2. Gyroscope measurement model The ﬁrst-order measurement model of gyroscopes is given by: rCr qCq p ωp + b + n + S) T s ωm = (I (6) The ωm is measured along the sensor’s sensitivity axes (the s frame) but the reference for the true excitation signal is the p frame. The composite matrix multiplying ωp above corresponds to a transfor- mation from the p to the s frame and corrects for the scale factor error.

G. Secer, B. Barshan / Sensors and Actuators A 247 (2016) 522–538 525 Fig. 3. ACUTRONIC FMS at (a) Step 1 and (b) Step 3 of the calibration procedure. The inset in part (a) shows the close-up view of the ﬁxture plate onto which the MicroStrain and Xsens units are attached. 2.3. Magnetometer measurement model Magnetometers are used to estimate the attitude of frame q with respect to the NED frame by measuring the Earth’s magnetic ﬁeld vector, denoted by BNED, with respect to the NED frame. However, in the real world, especially in indoor environments, magnetometers are exposed to more than just BNED. The presence of ferromag- netic materials and/or sources that radiate magnetic ﬁelds in the vicinity of the sensor are the main factors that affect the magnetic ﬁeld vector Bm measured by the sensor and cause deterioration.

526 G. Secer, B. Barshan / Sensors and Actuators A 247 (2016) 522–538 (I = r Cr r Cr qCq pCp q Cq p Cp qKCq + S)T s + S)T s r Cr + S) T s Having deﬁned H and b From Eq. (5), the coefﬁcient matrix H=(I NED for accelerometers, whereas, based on Eqs. (6) and (7), respectively, + H=(I p for gyroscopes and H=(I S)T s NED for magnetometers. Here, b is the uniﬁed bias vector, which is sim- ply equal to B for inertial sensors, whereas b qıB + b r Cr for magnetometers. , we note that both are functions of the calibration parameter vector . There are no additional con- straints on the choice of H and b. Furthermore, since sensors might undergo dynamic motions during the experiments, the term Cq p, appearing in H, is a time-dependent matrix, as is the excitation sig- nal e (whose time-dependence we have not yet shown explicitly to keep the notation simple). Thus, H(, t) : R3 and () : b R3, where we assume a constant bias model. The vector is determined by the parameters involved in the given mea- surement models and will be described for each different sensor type in the next section, while t denotes the time instant corre- sponding to the measurement. Finally, for all three types of sensors considered, we state that: H(, t) e(t) em(t) = = h(e, , t) Rdim() → Rdim() × + n(t) + n(t) + b R3 × () → (9) R 3. Sensor calibration Calibration is a multi-step procedure for improving position estimates by inverting the uniﬁed measurement model given in Eq. (9) to estimate the calibration parameter vector . The ﬁrst step requires designing an experimental procedure for data acquisition. In the second step, we implement parameter estimation algorithms based on the data acquired during the ﬁrst step. 3.1. Data acquisition tests Various test procedures are available to acquire data for esti- mating the calibration parameters of the different sensor types. Deterministic calibration methods can be divided into two classes: traditional and in-ﬁeld. Traditional methods are usually employed in the aerospace industry to calibrate tactical-grade IMUs, requiring highly expen- sive and specialized machines with accurate angular position- and/or velocity-control capability. Reference inputs are applied to the sensors at multiple positions to compare their measurements with and estimate the calibration parameters. The precise atti- tude at each position is required and reference inputs are used in component-wise form for this purpose. The precision of such machinery directly affects the estimation accuracy of the model parameters and the related cost increases proportionately. The choice of the test procedure depends on the type of machinery used. With the accelerated development of low-cost inertial sen- sors, the need for low-cost in-ﬁeld calibration techniques emerged, where the sensors are calibrated while operating in the ﬁeld, with- out the need for any additional actuators or sensors. Because of the limitations of these techniques, however, attitude information and consequently, component-wise reference inputs, such as the components of gNED and BNED, are not available to calibrate accele- rometers and magnetometers, respectively. Instead, the magnitudes (norms) of the reference inputs are compared with those of the gNED, thus, sensor measurement vectors since eliminating the need for projecting excitation signals onto the q frame [24,32]. However, when low-cost in-ﬁeld calibration tech- niques are used, it is neither possible to detect the misalignment matrix Cr NED. Furthermore, when using only the magnitudes of the reference inputs, the choice of the form of the matrix T s r is no longer trivial. This is because the order of the orthogonalization gNED q nor Cp Cq p Cp NED = Fig. 4. The r and s frames and their unit vectors. The related errors are divided into two classes: soft- and hard-iron errors [29,30]: Soft-iron errors are caused by the interaction of an external magnetic ﬁeld with ferromagnetic materials in the vicinity of the sensor [29]. The magnetic permeability of materials has a direct inﬂuence on this interaction. Soft-iron errors can be represented by a symmetric matrix K. Since its elements satisfy kij = kji, where i, j = 1, 2, 3 because of symmetry, the matrix has six independent elements. ıBy [ ıBx ıBz ]T . Hard-iron errors are time-invariant, undesired magnetic ﬁelds generated by ferromagnetic materials with permanent magnetism that are part of the structure of the platform onto which the sen- sors are mounted, or are part of equipment installed near the magnetometer [30]. Magnetic ﬁelds radiated by actuators such as electrical motors on gimbaled systems and constant magnetic ﬁelds in the test environment are some examples. The effect of these on the sensor axes could be time varying and orientation dependent because of the relative motion between the sensors and the envi- ronment. The resultant magnetic ﬁeld is a combination of BNED and ıB, where ıB = Modifying Eq. (5) to include K and ıB for soft- and hard-iron errors and replacing the excitation signal and the measured output with BNED and Bm, respectively, we obtain the traditional ﬁrst-order measurement model of magnetometers [29,31]: Bm = (I (7) + S) It for magnetometers, + b. Here, the excitation signal BNED T s rCr is with respect to the NED frame, whereas Bm is measured along the sensitivity axes of the magnetometer (the s frame). Thus, the composite matrix multiplying BNED in the above equation represents a transformation from the NED to the s frame and corrects for the scale factor and soft-iron errors. follows pCp q(KCq that BNED + + b + n BNED + h(e, ) + S) T s q(KCq ıB) ıB) = (I pCp rCr NED NED 2.4. The uniﬁed measurement model The measurement models of inertial sensors and magnetome- ters, represented by Eqs. (5)–(7) have some similarity. Generalizing the three equations into a uniﬁed measurement model: em = + n + b He (8)

G. Secer, B. Barshan / Sensors and Actuators A 247 (2016) 522–538 527 process determines the unknown matrix Cr q, and affects the results, as the installation is still made with respect to the IMU casing. This is not the case when using component-wise reference inputs, where the matrix Cr q compensates for the difference. Below, we give a brief description of the typical calibration approach for each sensor type used in this study: • Accelerometer: Accelerometers are traditionally calibrated by using angular position-control or centrifuge machines. In the former, the accelerometer is positioned and held stationary at various known reference orientations throughout the test. This is known as the multi-position or the 1g test. Calibration parame- ters are estimated based on the acquired sensor measurements and the reference accelerations associated with the reference ori- entations (i.e., the local gravity vector g) [10]. The limitation of this procedure is that the reference acceleration inputs applied to the sensors are restricted to the [−g, +g] interval, which may result in inaccurate calibration outside this interval. When cen- trifuge machines are used, reference acceleration inputs are not necessarily restricted to the [−g, +g] interval and higher accelera- tion values are sustainable [33]. Deterministic error components can then be identiﬁed in the same way as in the former procedure. • Gyroscope: The way calibration tests are performed for gyro- scopes depends on the quality grade of the device. High-precision gyroscopes are capable of measuring the Earth’s angular velocity, enabling the use of multi-position tests. Gyroscopes can be pos- itioned at reference orientations and the calibration parameters can be estimated by comparing the sensor measurements with the reference angular rate (the Earth’s angular velocity ω) at these positions [10]. However, lower-grade MEMS gyroscopes cannot be calibrated this way because they are not capable of sensing ω [34]; they need to be exposed to different reference angular veloc- ities that can be provided by an angular position-control machine or a single-axis rate table [35]. The latter allows accurate calibra- tion over a broader operation range compared to the former. The calibration parameters can be estimated by comparing the sensor measurements with the reference angular rates [36–38]. If such reference angular rates are not available, alternative techniques are required: (i) calibrated accelerometers and/or magnetome- ters, embedded in the sensor unit together with the gyroscope, can be used to provide the reference information. If accelero- meters are employed, measurements at stationary positions are compared with the gravity projected onto the sensor sensitivity axes by an angular transformation computed using gyroscopic measurements [39,40]. However, accelerometers are only able to detect the two angles between the sensor and the local horizontal direction [41]; their measurements cannot resolve the rotation about the local vertical direction (the yaw angle). Alternatively, embedded magnetometers that project the Earth’s magnetic ﬁeld onto the sensor’s sensitivity axes as reference information can be used [42]. Calibration is commonly performed by simply rotat- ing the sensors by hand on a ﬂat surface. (ii) when there is no additional sensor embedded in the sensor unit, the gyroscope can be ﬁxed to one of the contact surfaces of a right-angled plate and rotated by hand on a ﬂat surface. In this case, the attitude computed by gyroscope measurements is compared with the reference attitude associated with the plate’s conﬁguration [43]. • Magnetometer: Magnetometers are also calibrated based on data acquired during multi-position tests. The reference input is the Earth’s local magnetic ﬁeld vector BNED [29,31,44–46]. Mag- netometers need to undergo testing on the platform on which they will be eventually used (e.g., an aircraft or unmanned ground vehicle), and their calibration parameters need to be estimated speciﬁcally for this platform. The orientation of the platform is often controllable and it is capable of producing the motions required for the multi-position test [31,47,48]. When this is the case, the interior effects of the platform (e.g., the magnetic permeability of the material of the test bed) can be modeled as constant time-invariant distortion since there is no relative motion between the platform and the magnetometer. However, the platform and the magnetometer are usually not isolated from the environment. External magnetic sources such as electric motors or transformers may affect the magnetometer measure- ments [29,46] and contribute additional time-varying distortion components [49,50]. Despite that, in most of the earlier studies, such external distortion components are assumed to be constant for a given calibration platform. Considering this deﬁciency of the traditional methods, we present an extended measurement model accounting for the time-varying magnetic distortions that are often encountered in non-isolated test platforms, where there is relative motion between the magnetometer and the distortion sources in the environment. In the present study, we use ACUTRONIC’s high-precision 3-DoF FMS to conduct multi-position tests for the deterministic calibra- tion of our sensors. The FMS and its rotation axes are illustrated in Fig. 3 and the technical speciﬁcations can be found in [51]. Both units are mounted side by side to the FMS’s ﬁxture plate, located on the shaft of the inner axis. This is illustrated in the inset of Fig. 3(a). Then, a trajectory for the FMS axes, which is called a calibration procedure, is determined for the experiments and programmed into the FMS controller computer. The steps of the calibration procedure are summarized below, where the rota- tion angles are stated according to the right-hand rule so that positive-valued angles indicate a counter-clockwise rotation about the corresponding axis: shown in Fig. 3(a). 1. The inner axis of the FMS is aligned with the ground level, as 2. The inner axis of the FMS is rotated by 270◦ in 12 steps of 22.5◦ each. The FMS is held stationary at each one of those steps for 12.5 s. vector g, as shown in Fig. 3(b). stops and waits for 12.5 s at each step of 22.5◦. 3. The inner axis of the FMS is aligned with the vertical gravity 4. The FMS makes a half turn (180◦) around its middle axis while it 5. The FMS is taken back to its angular position at Step 3. 6. The inner axis of the FMS is rotated by 90◦. 7. The FMS performs the same motion as in Step 4. While designing this multi-position calibration procedure, it is necessary to ensure that the accelerometers and magnetometers experience a complete set of reference inputs. 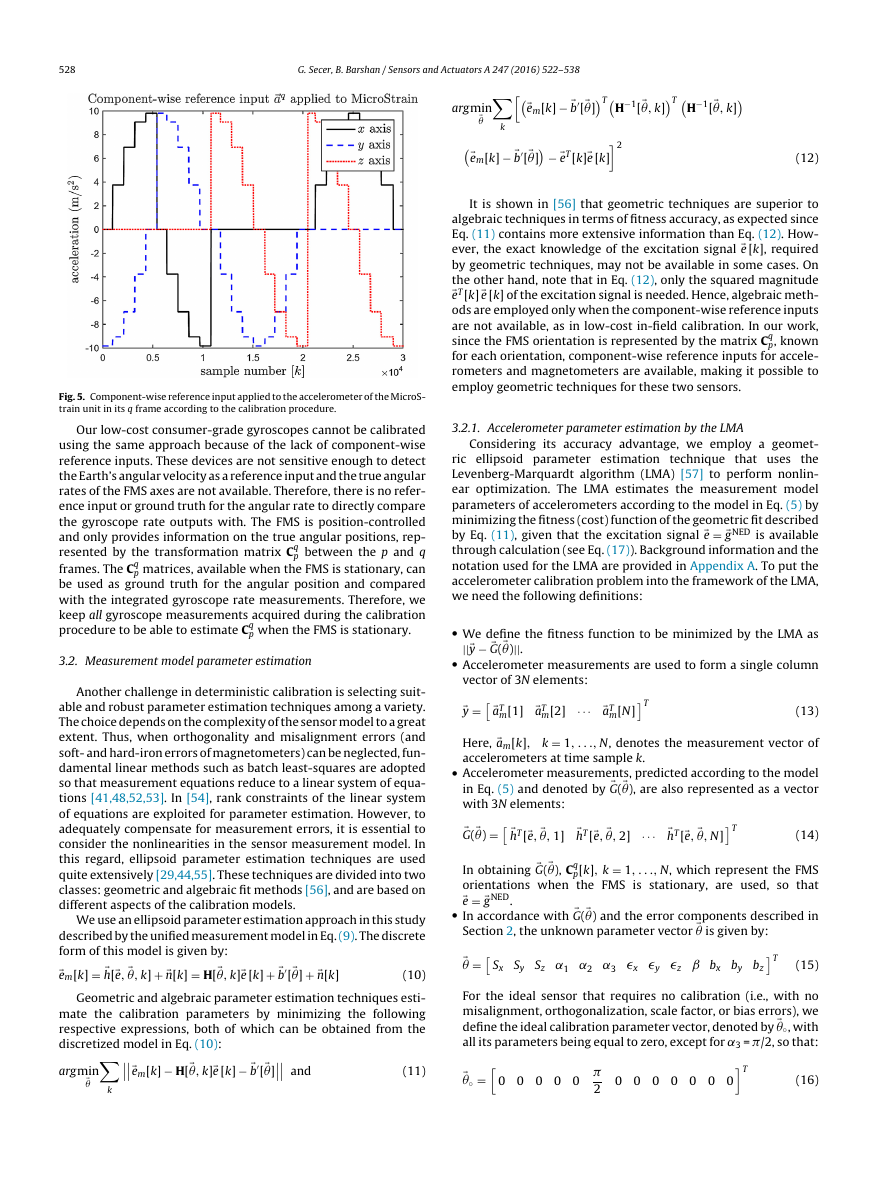This is illustrated in Fig. 5 where the component-wise reference acceleration input applied to the MicroStrain unit is provided as an example. During the calibration procedure, the accelerometer, gyroscope, and mag- netometer outputs of both units are recorded simultaneously at a uniform sampling rate of 100 Hz. To avoid additional disturbance on the measurements that might occur while the FMS is in motion, we only consider the accelerometer and magnetometer measurements acquired during the 12.5-s periods when the FMS is stationary. The local gravity and magnetic ﬁeld vectors, gNED and BNED, can be calculated/looked up and used as reference inputs in their component-wise form for the accelerometer/magnetometer measurements at these station- ary positions, respectively. Thus, the measurements acquired at these stationary positions are kept and processed, while the rest are discarded. The time indices in this subset of N elements are renumbered as a consecutive array. The ﬁnal form of this subset is denoted by Ns.

528 G. Secer, B. Barshan / Sensors and Actuators A 247 (2016) 522–538 em[k] k em[k] [] T [] 2 − eT [k]e [k] − b H − b argmin T −1[, k] −1[, k] H (12) It is shown in [56] that geometric techniques are superior to algebraic techniques in terms of ﬁtness accuracy, as expected since Eq. (11) contains more extensive information than Eq. (12). How- ever, the exact knowledge of the excitation signal e [k], required by geometric techniques, may not be available in some cases. On the other hand, note that in Eq. (12), only the squared magnitude eT [k] e [k] of the excitation signal is needed. Hence, algebraic meth- ods are employed only when the component-wise reference inputs are not available, as in low-cost in-ﬁeld calibration. In our work, since the FMS orientation is represented by the matrix Cq p, known for each orientation, component-wise reference inputs for accele- rometers and magnetometers are available, making it possible to employ geometric techniques for these two sensors. 3.2.1. Accelerometer parameter estimation by the LMA technique that uses Considering its accuracy advantage, we employ a geomet- ric ellipsoid parameter estimation the Levenberg-Marquardt algorithm (LMA) [57] to perform nonlin- ear optimization. The LMA estimates the measurement model parameters of accelerometers according to the model in Eq. (5) by minimizing the ﬁtness (cost) function of the geometric ﬁt described by Eq. (11), given that the excitation signal e = gNED is available through calculation (see Eq. (17)). Background information and the notation used for the LMA are provided in Appendix A. To put the accelerometer calibration problem into the framework of the LMA, we need the following deﬁnitions: (13) m[1] T aT m[N] aT − G()||. • We deﬁne the ﬁtness function to be minimized by the LMA as ||y • Accelerometer measurements are used to form a single column vector of 3N elements: y = aT · · · m[2] Here, am[k], k = 1, . . ., N, denotes the measurement vector of accelerometers at time sample k. • Accelerometer measurements, predicted according to the model in Eq. (5) and denoted by G(), are also represented as a vector with 3N elements: G() hT [e, , 2] In obtaining G(), Cq = 1, . . ., N, which represent the FMS orientations when the FMS is stationary, are used, so that e = gNED. • In accordance with G() and the error components described in Section 2, the unknown parameter vector is given by: T = Sx Sy Sz ˛1 ˛2 ˛3 x y z ˇ bx by bz hT [e, , 1] hT [e, , N] p[k], k T (14) (15) = · · · For the ideal sensor that requires no calibration (i.e., with no misalignment, orthogonalization, scale factor, or bias errors), we deﬁne the ideal calibration parameter vector, denoted by ◦, with all its parameters being equal to zero, except for ˛3 = /2, so that: ◦ = 0 0 0 0 0 0 0 0 0 0 0 0 T (16) 2 Fig. 5. Component-wise reference input applied to the accelerometer of the MicroS- train unit in its q frame according to the calibration procedure. Our low-cost consumer-grade gyroscopes cannot be calibrated using the same approach because of the lack of component-wise reference inputs. These devices are not sensitive enough to detect the Earth’s angular velocity as a reference input and the true angular rates of the FMS axes are not available. Therefore, there is no refer- ence input or ground truth for the angular rate to directly compare the gyroscope rate outputs with. The FMS is position-controlled and only provides information on the true angular positions, rep- resented by the transformation matrix Cq p between the p and q frames. The Cq p matrices, available when the FMS is stationary, can be used as ground truth for the angular position and compared with the integrated gyroscope rate measurements. Therefore, we keep all gyroscope measurements acquired during the calibration procedure to be able to estimate Cq p when the FMS is stationary. 3.2. Measurement model parameter estimation Another challenge in deterministic calibration is selecting suit- able and robust parameter estimation techniques among a variety. The choice depends on the complexity of the sensor model to a great extent. Thus, when orthogonality and misalignment errors (and soft- and hard-iron errors of magnetometers) can be neglected, fun- damental linear methods such as batch least-squares are adopted so that measurement equations reduce to a linear system of equa- tions [41,48,52,53]. In [54], rank constraints of the linear system of equations are exploited for parameter estimation. However, to adequately compensate for measurement errors, it is essential to consider the nonlinearities in the sensor measurement model. In this regard, ellipsoid parameter estimation techniques are used quite extensively [29,44,55]. These techniques are divided into two classes: geometric and algebraic ﬁt methods [56], and are based on different aspects of the calibration models. We use an ellipsoid parameter estimation approach in this study described by the uniﬁed measurement model in Eq. (9). The discrete form of this model is given by: em[k] H[, k]e [k] = = h[e, , k] + n[k] + n[k] + b [] (10) Geometric and algebraic parameter estimation techniques esti- mate the calibration parameters by minimizing the following respective expressions, both of which can be obtained from the discretized model in Eq. (10): argmin em[k] and H[, k]e [k] − − b [] (11) k

G. Secer, B. Barshan / Sensors and Actuators A 247 (2016) 522–538 529 Considering the centrifugal acceleration effects caused by the Earth’s rotation, the value of gNED at the location where the exper- iments are conducted can be calculated using [10]: gNED = g − (R ) ωNED2 + 2 sin 2 0 + cos 2) (1 (17) T where g = [0 0 9.80665]T m/s2 is the standard gravity vector and ωNED, R, , and represent the Earth’s angular velocity vector with respect to the NED frame, the radius of the Earth, altitude with respect to sea level, and the latitude angle that changes between −90◦ and 90◦, respectively. The calculated gNED vector is given by gNED = [−0.0167 0 9.7782]T m/s2. 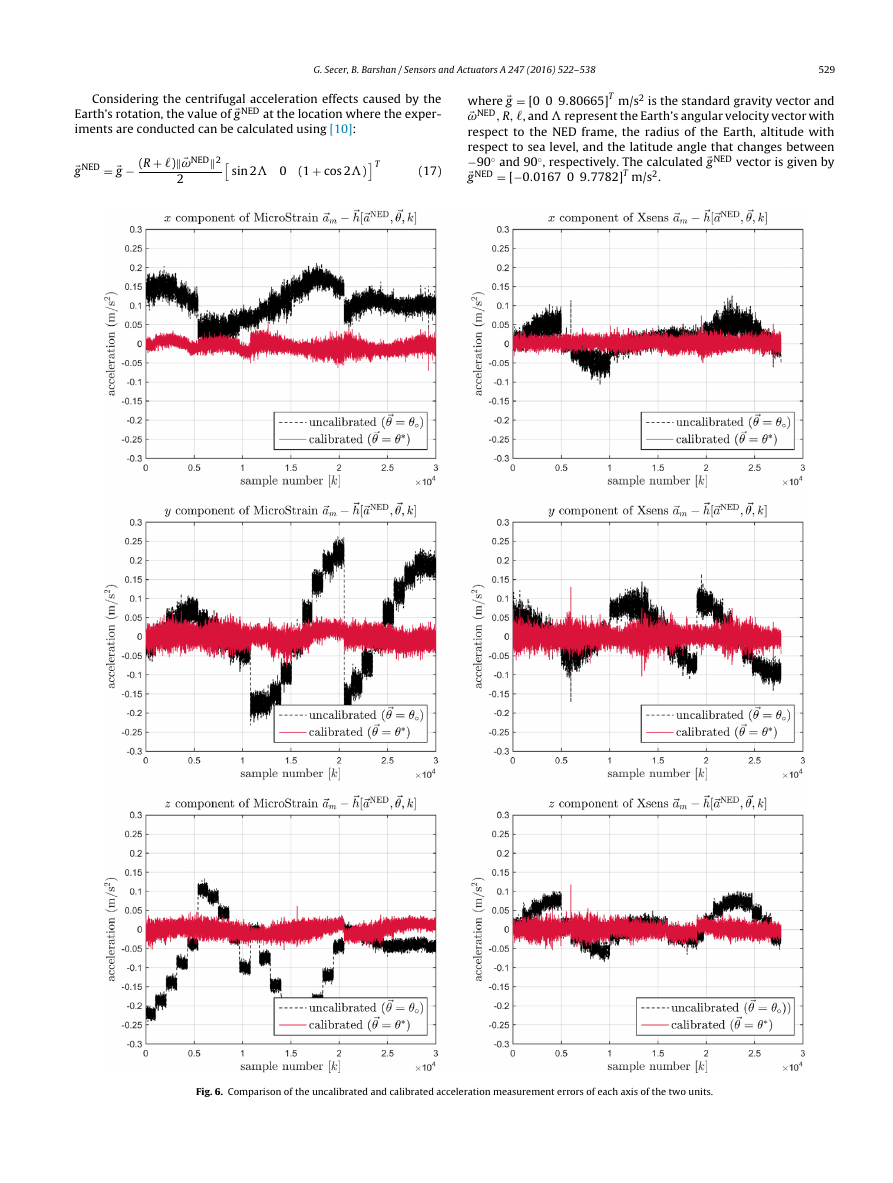Fig. 6. Comparison of the uncalibrated and calibrated acceleration measurement errors of each axis of the two units.

资料库

惯性传感器和磁力计的确定性误差建模和校准的改进.pdf

相关推荐

开发技术

热门标签

最新资料