logo资料库

论文研究-OFDM/OQAM系统自适应滤波器函数波形设计 .pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.51M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn OFDM/OQAM 系统自适应滤波器函数波形设计 王丽娟1，孙志国2** （1. 哈尔滨工程大学信息与通信工程学院，哈尔滨市 150001； 2. 通信网信息传输与分发技术重点实验室，石家庄市 050000） 摘要：传统的 OFDM 系统通过添加 CP 来提高系统抗 ISI 的能力，其不足是降低频谱利用率， 且系统对频偏敏感的问题没有的到解决。该文讨论的是改进型 OFDM/OQAM 系统，其采用了时 频聚焦特性良好的成型滤波器函数，在系统不需要添加 CP 的情况下，仍然具有很好抗 ISI 和 ICI 的能力。首先，文章讨论如何进行 OFDM/OQAM 系统成型滤波器函数的选取。然后，讨 论了基于扩展高斯函数的 OFDM/OQAM 系统自适应滤波器波形设计方法，并得出结论。最后在 不同信道扩展高斯函数不同扩展因子下进行性能分析。仿真结果验证了该方法的有效性。 关键词：OFDM；OFDM/OQAM；扩展高斯函数；时频聚焦 中图分类号：TN914.3 Design of adaptive filter function waveform in OFDM/OQAM system WANG Lijuan1, Sun Zhiguo2 150001; (1. Information and Communication Engineering School, Harbin Enginneering University, Harbin 2. Information Transmission and Distribution Technology Key Laboratory, Shijiazhuang 050000) Abstract:The traditional Orthogonal Frequency Division Multiplexing (OFDM) system increases the ability to resist Inter Symbol Interference (ISI) by adding Cyclic Prefix (CP). However, the drawback is inefficient spectrum utilization and not solving the problem of system’s sensibility to frequency offset. This paper discusses an improved Orthogonal Frequency Division Multiplexing/Offset Quadrature Amplitude Mudulation (OFDM/OQAM) system, which uses the pulse-shaping filter function with good time-frequency localization. It has good robustness against ISI and ICI (Inter Carrier Interference) without adding CP. Firstly, the paper discusses how to select the shaping filter function of OFDM/OQAM system. Then, the adaptive filter waveform design method of OFDM/OQAM system based on EGF (Extended Gaussian Function) is discussed. Finally, the simulation result of the performance of different channel EGF function under different expansion factors is given, which verifies the effectiveness of this kind of method. Keywords: OFDM; OFDM/OQAM; Extended Gaussian Function; Time Frequency Localization 5 10 15 20 25 30 35 0 引言 40 正交频分复用（OFDM）作为多载波调制技术的典型，90 年代已经在各个领域得到广 泛的应用。其中 4G 中的空中接口方案就是用的 OFDM 技术，在对抗多径信道下表现出来 优越的特性。OFDM 是一种有效的多载波技术，利用不同子载波正交特性达到系统频谱效 率最大化。尽管传统的 OFDM 系统通过添加循环前缀（CP）来有效的消除多径干扰，但是 其还是有两个缺点：（1）系统加入了循环前缀，使得频谱的利用率降低；（2）采用矩形脉 冲滤波器函数，该函数的旁瓣较高，因此导致系统对频偏敏感。 在当前频谱资源稀缺的环境下，正交频分复用/交错正交幅度调制（OFDM/OQAM）系 统受到了广泛的关注[1]。随着人们对通信速率和质量的要求不断提高，在马上到来的 5G 技 作者简介：王丽娟（1991-），女，学生，通信对抗 通信联系人：孙志国（1977 年-），男，硕导，主要研究方向：通信对抗. E-mail: sunzhiguo@hrbeu.edu.cn - 1 -
    45 50 55 60 65 70 中国科技论文在线 http://www.paper.edu.cn 术中，OFDM 技术已经远远达不到标准。因此越来越多的研究者开始关注 OFDM/OQAM 技 术，其成为 5G 通信标准的热门人选。 为了改善传统OFDM 抗符号间干扰（Inter Symbol Interference，ISI）和子载波间干扰（Inter Carrier Interference，ICI）的能力，OFDM/OQAM 系统采用了时频聚焦特性良好的滤波器[2]。 这样使得系统在不需要添加 CP 的情况下，仍然具有良好的抗 ISI 和 ICI 的性能。但其代价 就是该通信系统的子载波不是严格意义上的正交，而是实数域正交。这就使得 OFDM/OQAM 系统中的关键技术与传统 OFDM 的实现方法不同，这也是我们之后将要研究的重点。 本文的主要内容是，选取时频聚焦特性良好的高斯扩展函数（EGF）作为 OFDM/OQAM 系统的滤波器函数，根据其特性，分析不同信道下所对应的滤波器函数波形，使通信系统有 更好地性能[3][4]。下面将首先介绍一下 OFDM/OQAM 的系统模型，然后在介绍 OFDM/OQAM 系统中选取滤波器函数的依据以及自适应滤波器函数波形设计的方法，最后根据前面的原 理，进行性能仿真和结果分析。 1. OFDM/OQAM 系统模型 OQAM 串/并转换 IFFT 多相滤波器组 （IOTA）   并/串转换 信道 图 1 OFDM/OQAM 系统发送端的框图 Fig.1 Block diagram of OFDM/OQAM system transmitter 图 1 是 OFDM/OQAM 系统发送端的系统框图，假设 DM/OQAM 系统接收端的数学模 型为： s t ( )   N 1    a g m n m n , , t ( )   N 1    a e m n , jπ( m n  )/2 jπ m t  0 e g t n (   0 ) （1）  0 n ,  m   n Z m  n m 0   N m na 式中： , ( 1) 0,1,...  表示在数据处于时频格点的第 n 个符号内的第 m 个子载 波上，其实这里是类比于 OFDM/OQAM； 0 和 0 分别表示 OFDM/OQAM 时频网格中数据 的时域持续时间和频域持续时间,且 0 0 1/ 2 ；前面已经介绍了，OFDM/OQAM 系统是正 交的，那么它的正交性是如何体现的呢，接收端如保证解调效果呢，为了便于分析和解释 OFDM/OQAM 接收解调原理，分析基函数 , ( ) t 的正交性，则：   m ng g m n , t g ( ), * p k , t ( )   Re{ R R e Re{ j(  e j( m n p k    )π/2 j2π( m p  )  0 t e m n p k    )π/2  R g t n (   0 g t k *  (  0 )} ) g t n (   0 g t k ( *  m t  j2π e )  0  j2π p t  e ) } （2）  令 t n   0   x ( g m n , t g ( ), p k , t ( ) R k n ) / 2   0 πj 2 e Re{  (( ，则上式可以重写为： m n p k ) (     m p n k  )(  ))  R g x (  )  0 ( k n  2 ) g x ( *  )  0 )} ( k n  2 （3）  πj 2  e Re{ (( m n p k ) (     m p n k  )(  )) A k n   g 0 (( ),( p m )  0  )} 式中： ( , ) gA  是模糊函数，其定义为： - 2 -
    中国科技论文在线 http://www.paper.edu.cn A g t e ( , ) ( , )       gR j2π t  dt  e  R  j2π t  g t (   g t ) ( * 2  t )d  2 （4）  模糊函数通常应用于雷达上面，它一种分析时频二维域的一种有效的工具，在这里借鉴 过来，是来自对于 TFL 的讨论，简单理解 OFDM/OQAM 中的模糊函数就是在时间和频率上 的相关程度。 n k  n k 1 ( n k  满足互异性，即如果 n k 是偶    n k  为奇数(偶数)，所以，综合式（3）与式（4），实正交条件可重新表 1 1)  ， n k 与 (2  1 k ) 考虑到 数(奇数)，则 示为： g m n ,   t g , p k ,   t R    A g     k n k n ,      0   k n  或者 0   或者  p m   0   为偶数  p m   p m  为奇数   （5） 由 0 0 1/ 2   可知，当成形滤波函数 ( )g t 满足下式即可实现实正交条件： 则重写正交性表达式，可得： A g (2 p   0 0 ,2 q )  { 1 0 p p   q 0 且 q 0 或   0 0 （6） g m n , t g ( ), p k , t ( ) R  g t g ( ) * p k , m n , R  Re{ e Re{   m p n k , j(( ,   t t ( )d } π 2 )( )) m n p k ) (     m p n k   A k n  g (( )  0 ,( p m  )  0 )} （7）  75 80 85 在这里需要说明的是，系统解调后接收端如果不取实数的情况下，得到的是一个复数值， 其中的实数是所需要的，而虚部那一部分则是要丢弃的，而 OFDM/OQAM 实正交也是这么 来的。 2. OFDM/OQAM 系统的自适应滤波器波形设计 90 2.1 OFDM/OQAM 系统滤波器的选取 如上述所述，OFDM/OQAM 使用了与传统 OFDM 不同的基函数，其中扩展高斯函数 （EGF）被大量的文献所提到。本文是选取 EGF 来完成 OFDM/OQAM 系统自适应波形设计， 首先简单介绍一下该函数的性质及应用。EGF 函数是由高斯函数通过时域和频域的两次正 95 交得到的，其表达式 示： vz   可通过逼近算法，由一组封闭解析式的加和来表述，如下所 , t , ( ) 0 0 z   0 v 0 , , t ( )  1 2      k  0 d k , ,  v 0    g t (   k v 0 )  g t (   ) k v 0         g t    l  0 d l ,1/ ,  0 cos(2 l  t  0 ) （8）    1 4  2  2 e  t  ,  （9）  0 l   2 2  0 a e k l , ,0    k （10）    l  0 d k ,  0 ,  - 3 -
    100 105 110 115 120 125 中国科技论文在线 http://www.paper.edu.cn v 0.528 0 v  ， d  为实数[5]。因 式中： 0 0 1 2 k 为该函数家族源于高斯函数，故称之为拓展高斯函数。而且 EGF 函数具有如下傅里叶变换 对称关系： ， g即为高斯函数，系数 v 7.568 0   v 0 2 2 , ,  FT z 0 ,   0 ,  z 1 ,   0 0 , （11）  2 0 1    并且当 1 ， 0 时，EGF 的傅里叶变换等于其本身，此时的 EGF 被称为 各向同性正交转换算法（Isotropic Orthogonal Transform Algorithm，IOTA）。即 IOTA 函数 只是 EGF 家族中的一个特例，它所拥有的正交特性和良好的时频局部化特性，EGF 函数系 列均共享。在实际应用中，EGF 的加和次数不可能无穷大，一般截断取前 50 项即可保持较 好的正交性和 TFL[6]。为了比较不同成型函数波形的时频聚焦特性，引入海森伯格参数，定 义如下：   1 t f 4     1 （12）  式中： t 和 f 分别表示成型函数的能量延时间和频率域的扩散程度，定义为：   2 t g t 2    t 2    f G f 2   f 2    dt （13）   2 df （14）  即扩散值越小，海参伯格参数越大，此时成型函数的时频聚焦特性越好，抵抗信道干扰 弥散带来的 ISI 和 ICI 干扰的能力越强。下表是几种常见函数的海参伯格参数。 由表 1 可以看到高斯函数具有最大的海参伯格参数，但是由于其是非正交的，因而无法 应用于 OFDM/OQAM 系统中。因此我们选择了 EGF 函数来实现 OFDM/OQAM 系统抗时频 双选信道的性能。 表 1 不同成型函数海森堡伯格参数表 Table1 Heisenberg parameters of different forming functions    成型波形  半余弦  0.895  2.2 OFDM/OQAM 系统自适应波形设计 矩形  0.178  根升余弦  高斯函数  0.888  1  EGF  0.977  考 虑 到 EGF 在 不 同 扩 展 因 子 情 况 下 的 波 形 不 同 ， 本 文 对 基 于 该 滤 波 器 函 数 的 gA  进行分析，其中模糊函 OFDM/OQAM 系统的模糊度函数[7]（Ambiguity Function）   , 数定义为： gA   ,   e   j t 2   g t     2    * g    t    d  2  t （15）  模糊度函数是关于时间和频域的二维函数，可以反映出 OFDM/OQAM 系统的时频特性。 首先来证明 EGF 函数的时域扩展特性[8]，由高斯函数的时域表达式式（9），得其时域扩展 函数为： - 4 -
    130 135 140 中国科技论文在线 http://www.paper.edu.cn   1 4  2  e 2      t s     g     t s    s 2     s 2 1 4       2 s 2 t e    t （16）  s g   2 s 此外，对于 EGF 函数系数序列 kd  而言，该序列满足： , , 0  结合式（8）、式（16）和式（17）可得： ,  0  d  0 k l , a e k l ,   l  2 2  0    l  0 2 s   l     2 s 2  0  a e k l ,  d k 2 ,   0 s , z   0 0 , , t s    d k ,  0 ,    g  t s     k  0     g  t s     k  0             l  0 d l ,1 ,  0  cos 2   l  t s  0    （17）  s （18）       0 k       s  2   k s z  1= 2 = =    0 d k ,  0 2 , s s , s  0  2 s  0 , s   t     g  2 s    t  k  0    s  g t      2 s k  0 s              l  0 d l ,1   2 s  ,s  0  cos 2   l  t s  0    通过采样时间间隔 sT N 02 和简单的数学推导和变量替换，可得基于 EGF 函数的 OFDM/OQAM 系统的模糊函数满足：  2       0   2    0    2 2    A g     ,    A g     0 , 1   0    （19） 由上式可得，基于 EGF 函数的 OFDM/OQAM 系统通过调整扩展因子可以改变系统 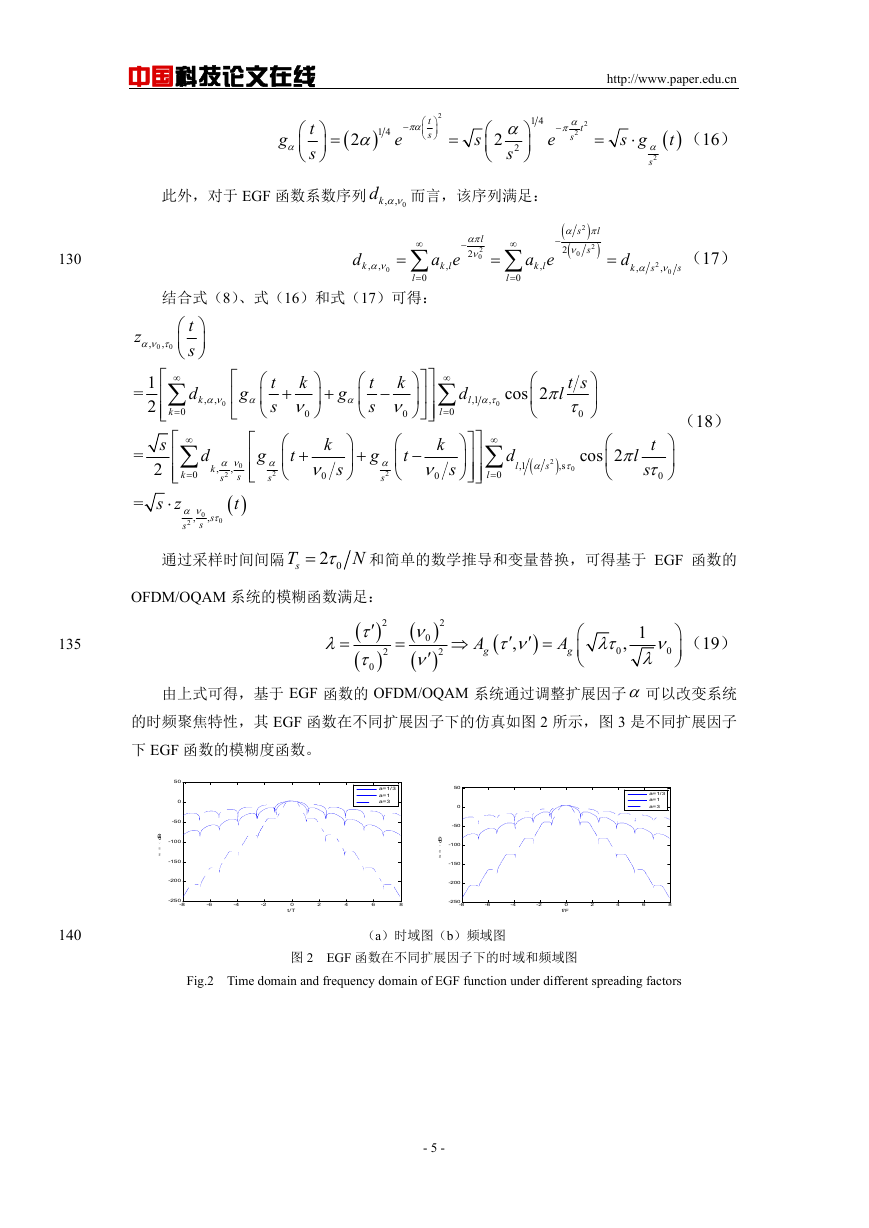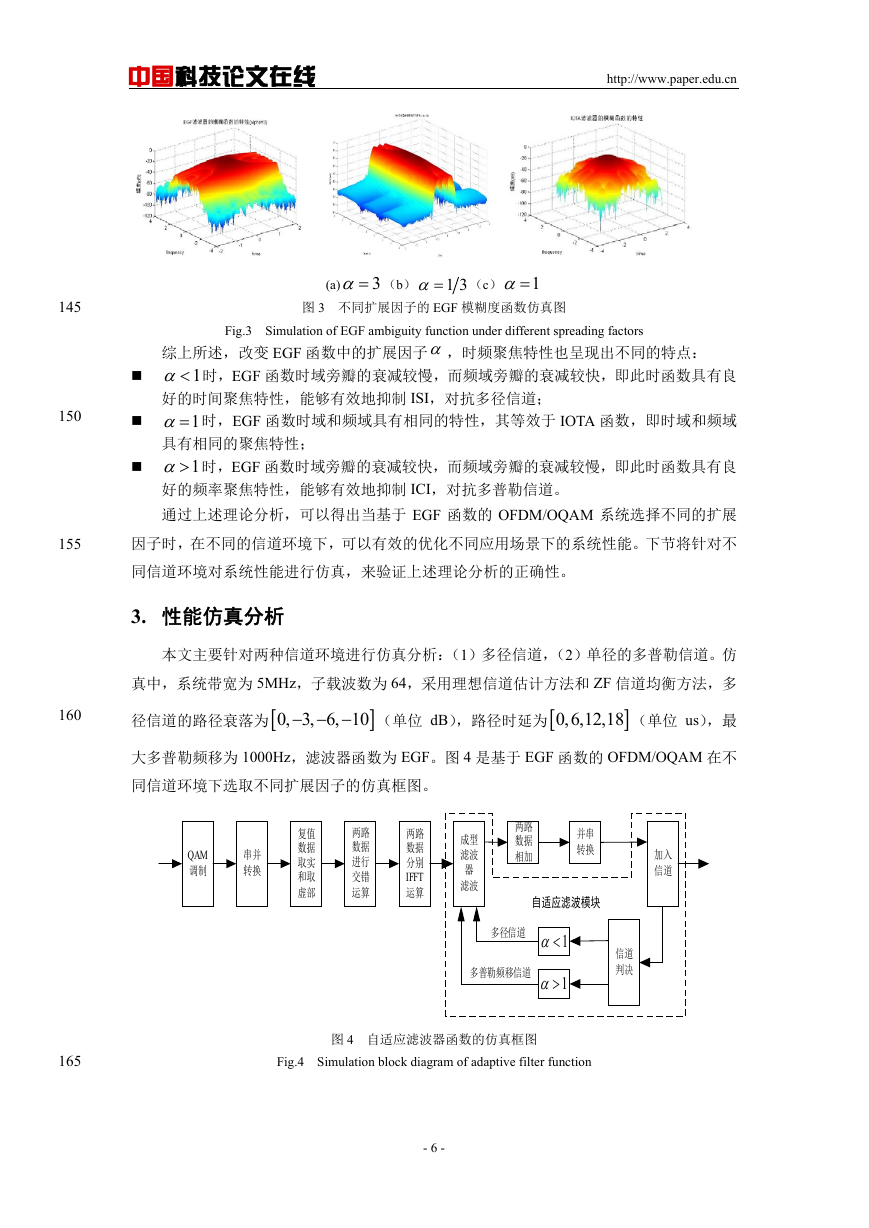的时频聚焦特性，其 EGF 函数在不同扩展因子下的仿真如图 2 所示，图 3 是不同扩展因子 下 EGF 函数的模糊度函数。 50 0 -50 -100 -150 -200 ） B d （ 度 幅 a=1/3 a=1 a=3 50 0 -50 -100 -150 -200 ） B d （ 度 幅 a=1/3 a=1 a=3 -250 -8 -6 -4 -2 0 t/T 2 4 6 8 -250 -8 -6 -4 -2 0 f/F 2 4 6 8   （a）时域图（b）频域图 图 2 EGF 函数在不同扩展因子下的时域和频域图 Fig.2 Time domain and frequency domain of EGF function under different spreading factors - 5 -
    中国科技论文在线 http://www.paper.edu.cn (a) 3 （b） 1 3 （c） 1 图 3 不同扩展因子的 EGF 模糊度函数仿真图      Fig.3 Simulation of EGF ambiguity function under different spreading factors 综上所述，改变 EGF 函数中的扩展因子，时频聚焦特性也呈现出不同的特点： 1 时，EGF 函数时域旁瓣的衰减较慢，而频域旁瓣的衰减较快，即此时函数具有良 好的时间聚焦特性，能够有效地抑制 ISI，对抗多径信道； 1 时，EGF 函数时域和频域具有相同的特性，其等效于 IOTA 函数，即时域和频域 具有相同的聚焦特性； 1 时，EGF 函数时域旁瓣的衰减较快，而频域旁瓣的衰减较慢，即此时函数具有良 好的频率聚焦特性，能够有效地抑制 ICI，对抗多普勒信道。 通过上述理论分析，可以得出当基于 EGF 函数的 OFDM/OQAM 系统选择不同的扩展 因子时，在不同的信道环境下，可以有效的优化不同应用场景下的系统性能。下节将针对不 同信道环境对系统性能进行仿真，来验证上述理论分析的正确性。 3. 性能仿真分析 本文主要针对两种信道环境进行仿真分析：（1）多径信道，（2）单径的多普勒信道。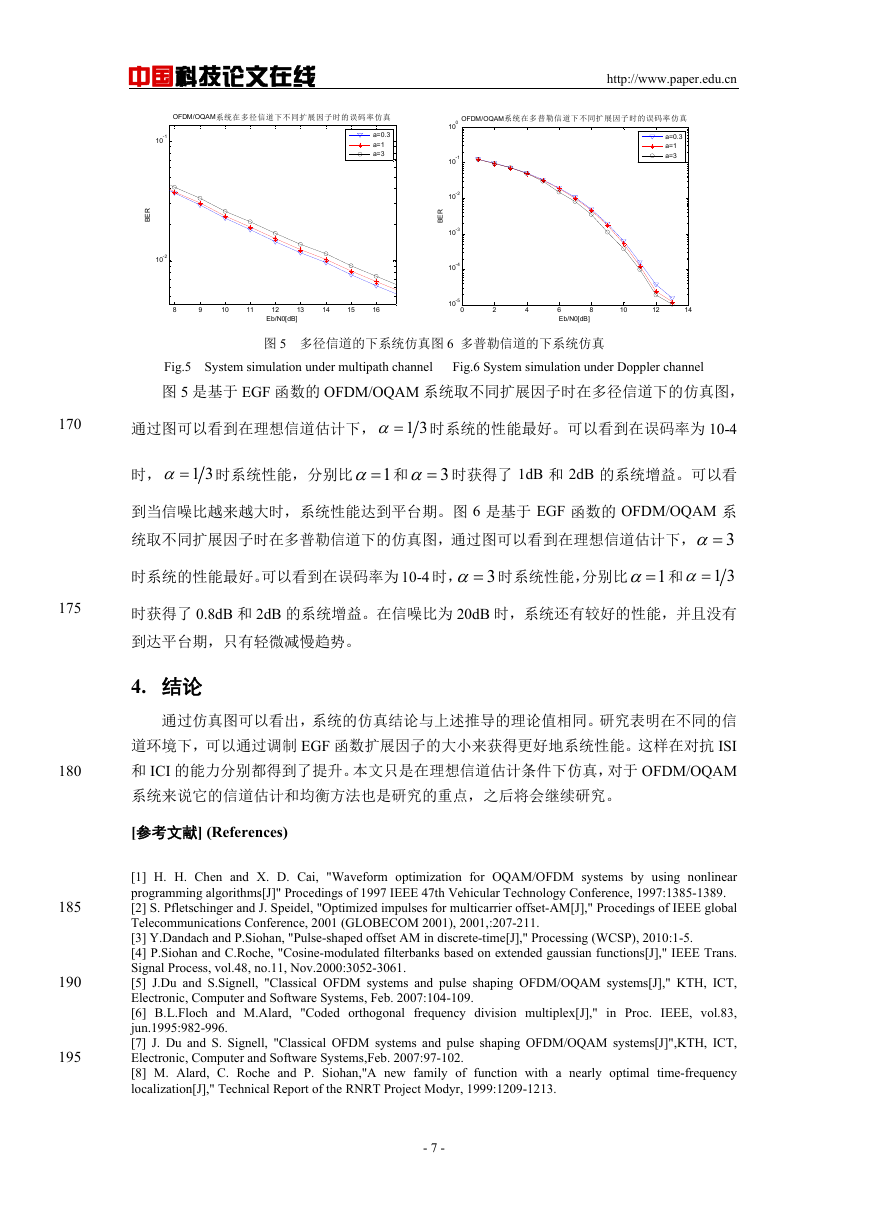仿 真中，系统带宽为 5MHz，子载波数为 64，采用理想信道估计方法和 ZF 信道均衡方法，多 径信道的路径衰落为 大多普勒频移为 1000Hz，滤波器函数为 EGF。图 4 是基于 EGF 函数的 OFDM/OQAM 在不 同信道环境下选取不同扩展因子的仿真框图。     （单位 dB），路径时延为 0,6,12,18 （单位 us），最 0, 3, 6, 10   145 150 155 160 QAM 调制 串并 转换 复值 数据 取实 和取 虚部 两路 数据 进行 交错 运算 两路 数据 分别 IFFT 运算 成型 滤波 器 滤波 两路 数据 相加 并串 转换 自适应滤波模块 加入 信道 多径信道 多普勒频移信道 1 1 信道 判决   165 图 4 自适应滤波器函数的仿真框图 Fig.4 Simulation block diagram of adaptive filter function - 6 -
    中国科技论文在线 http://www.paper.edu.cn OFDM/OQAM 系统在多普勒信道下不同扩展因子时的误码率仿真 a=0.3 a=1 a=3 OFDM/OQAM 系统在多径信道下不同扩展因子时的误码率仿真 a=0.3 a=1 a=3 10-1 R E B 10-2 100 10-1 10-2 10-3 10-4 R E B 8 9 10 11 12 13 Eb/N0[dB] 14 15 16 10-5 0 2 4 6 8 Eb/N0[dB] 10 12 14   图 5 多径信道的下系统仿真图 6 多普勒信道的下系统仿真 Fig.5 System simulation under multipath channel Fig.6 System simulation under Doppler channel 图 5 是基于 EGF 函数的 OFDM/OQAM 系统取不同扩展因子时在多径信道下的仿真图， 170 通过图可以看到在理想信道估计下， 1 3 时系统的性能最好。可以看到在误码率为 10-4 时， 1 3 时系统性能，分别比 1 和 3 时获得了 1dB 和 2dB 的系统增益。可以看 到当信噪比越来越大时，系统性能达到平台期。图 6 是基于 EGF 函数的 OFDM/OQAM 系 统取不同扩展因子时在多普勒信道下的仿真图，通过图可以看到在理想信道估计下， 3 时系统的性能最好。可以看到在误码率为 10-4 时， 3 时系统性能，分别比 1 和 1 3 时获得了 0.8dB 和 2dB 的系统增益。在信噪比为 20dB 时，系统还有较好的性能，并且没有 到达平台期，只有轻微减慢趋势。 4. 结论 通过仿真图可以看出，系统的仿真结论与上述推导的理论值相同。研究表明在不同的信 道环境下，可以通过调制 EGF 函数扩展因子的大小来获得更好地系统性能。这样在对抗 ISI 和 ICI 的能力分别都得到了提升。本文只是在理想信道估计条件下仿真，对于 OFDM/OQAM 系统来说它的信道估计和均衡方法也是研究的重点，之后将会继续研究。 [参考文献] (References) [1] H. H. Chen and X. D. Cai, "Waveform optimization for OQAM/OFDM systems by using nonlinear programming algorithms[J]" Procedings of 1997 IEEE 47th Vehicular Technology Conference, 1997:1385-1389. [2] S. Pfletschinger and J. Speidel, "Optimized impulses for multicarrier offset-AM[J]," Procedings of IEEE global Telecommunications Conference, 2001 (GLOBECOM 2001), 2001,:207-211. [3] Y.Dandach and P.Siohan, "Pulse-shaped offset AM in discrete-time[J]," Processing (WCSP), 2010:1-5. [4] P.Siohan and C.Roche, "Cosine-modulated filterbanks based on extended gaussian functions[J]," IEEE Trans. Signal Process, vol.48, no.11, Nov.2000:3052-3061. [5] J.Du and S.Signell, "Classical OFDM systems and pulse shaping OFDM/OQAM systems[J]," KTH, ICT, Electronic, Computer and Software Systems, Feb. 2007:104-109. [6] B.L.Floch and M.Alard, "Coded orthogonal frequency division multiplex[J]," in Proc. IEEE, vol.83, jun.1995:982-996. [7] J. Du and S. Signell, "Classical OFDM systems and pulse shaping OFDM/OQAM systems[J]",KTH, ICT, Electronic, Computer and Software Systems,Feb. 2007:97-102. [8] M. Alard, C. Roche and P. Siohan,"A new family of function with a nearly optimal time-frequency localization[J]," Technical Report of the RNRT Project Modyr, 1999:1209-1213. - 7 - 175 180 185 190 195
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料