logo资料库

数模论文-嫦娥三号软着陆轨道设计与控制策略.pdf

发布时间：2022-06-06 发布人：admin 分类：说明书 资料大小：0.90M 资料格式：pdf 举报 版权申诉
第1页 / 共28页
第2页 / 共28页
第3页 / 共28页
第4页 / 共28页
第5页 / 共28页
第6页 / 共28页
第7页 / 共28页
第8页 / 共28页
资料共28页，剩余部分请下载后查看
    赛区评阅编号（由赛区组委会填写）： 2018 高教社杯全国大学生数学建模竞赛 承 诺 书 我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参 赛规则》（以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。 我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网 上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。 我们知道，抄袭别人的成果是违反竞赛章程和参赛规则的，如果引用别人的成果或 资料（包括网上资料），必须按照规定的参考文献的表述方式列出，并在正文引用处予 以标注。在网上交流和下载他人的论文是严重违规违纪行为。 我们以中国大学生名和信重承诺，严格遵守竞赛章程和参赛规则，以保证竞 赛的公正、公平性。如有违反竞赛章程和参赛规则的行为，我们将受到严处理。 我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展 示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。 我们参赛选择的题号（从 A/B/C/D 中选择一项填写）： A 我们的报名参赛队号（12 位数字全国统一编号）： 参赛学校（完整的学校全称，不含院系名）： 参赛队员 (打印并签名) ：1. 解坤 华南理工大学 2. 丛天怡 3. 陈雪莹 指导教师或指导教师组负责人 (打印并签名)： 刘小兰 （指导教师签名意味着对参赛队的行为和论文的真实性负责） （请勿改动此页内容和格式。此承诺书打印签名后作为纸质论文的封面，注意电子版论 文中不得出现此页。以上内容请仔细核对，如填写错误，论文可能被取消评奖资格。） 日期: 2018 年 08 月 28 日
    赛区评阅编号（由赛区组委会填写）： 2018 高教社杯全国大学生数学建模竞赛 编 号 专 用 页 赛区评阅记录（可供赛区评阅时使用）： 评 阅 人 备 注 送全国评阅统一编号（由赛区组委会填写）： 全国评阅随机编号（由全国组委会填写）： （请勿改动此页内容和格式。此页和评，打印后 纸质论文的页上。注意电子版论文中不得出现此页。）
    嫦娥三号软着陆轨道设计与控制策略 摘要 嫦娥三号在高速飞行的情况下，要保证准确地在月球预定区域内实现软着陆，关键 问题是着陆轨道与控制策略的设计。 针对问题一，基于开普勒定律，求解着陆准备轨道方程，得嫦娥三号在远月点与近 月点的相应速度。将嫦娥三号的着陆轨道和着陆坐标结合，可求得近月点与月球心的相 对位置，结合椭圆公式可求得远月点坐标。确定了主减速阶段的运动轨迹后，嫦娥三号 的着陆轨迹也就基本确定了。本文在提出燃料最优制导律后，运用四阶 Runge-Kutta 函 数进行分段求解逼近，之后进行神经网络遗传算法寻优。 针对问题二，通过查阅相关资料，给出了软着陆各个阶段的动力学方程和制导律。 主减速段是耗时最长，燃料消耗最多的阶段，因此采用了燃料最优原则。快速调整阶段 利用推力大小和方向线性变化的制导律，满足主发动机推力和着陆器姿态匀速过渡的要 求。粗避障段垂直方向上采用燃料最优原则。为实现粗避障，本文采用对数字高层图进 行分块，计算各块方差后，设置一个合适的阈值，将分块分为安全区和危险区，再利用 动态规划的思想选取最大面积的连续安全区。精避障段同样采取燃料最优原则，并对高 层图进行分块，确定安全区与危险区。为了使最终着陆点与与着陆点接近，采用螺旋前 进搜索方法，搜索与中心点最近的着陆区。缓速下降段主要考虑的是着陆的安全性，故 使用匀变速直线运动模型。 针对问题三，在对模型的分析与检验中给出相应的误差分析。 关键字： 软着陆 燃料最优控制 Runge-kutta BP 神经网络 遗传算法 1
    目录 一、 问题重述 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1 . 1 背景 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1 . 2 需要解决的问题. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 二、 模型的假设 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 三、 符号说明 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 四、 问题一的模型建立与求解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 4 . 1 问题一分析 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 4 . 2 模型的建立 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 4 . 2 . 1 着陆准备轨道的运动学方程 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 4 . 2 . 2 主减速段的动力学方程 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 4 . 2 . 3 燃料最优控制律设计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 4 . 2 . 4 主减速阶段燃料最优控制模型描述 . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 4 . 2 . 5 远月点的位置 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 4 . 3 模型求解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 4 . 3 . 1 远月点和近月点的速度 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 4 . 3 . 2 燃料最优控制律的求解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 五、 问题二的建模与求解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 5 . 1 问题二分析 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 5 . 2 着陆准备阶段. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 5 . 3 主减速段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 5 . 4 快速调整段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 5 . 5 粗避障段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 5 . 5 . 1 基于数字高层图的安全区识别算法 . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 5 . 5 . 2 基于动态规划思想的着陆区选择算法 . . . . . . . . . . . . . . . . . . . . . . . . . 15 5 . 5 . 3 粗避障段的运动学模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 5 . 5 . 4 模型求解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 5 . 6 精避障段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 5 . 6 . 1 中心螺旋式安全着陆区搜索方法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 5 . 6 . 2 精避障段的运动学模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 5 . 6 . 3 模型求解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2
    5 . 7 缓速下降段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 六、 问题三 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 6 . 1 轨道方面 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 6 . 1 . 1 关于月球自转 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 6 . 1 . 2 关于轨道的确定 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 6 . 2 控制策咯方面. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 6 . 2 . 1 粗避障阶段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 6 . 2 . 2 精避障阶段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 6 . 3 精确分析 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 6 . 3 . 1 可见性分析 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 6 . 3 . 2 姿态分析 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 6 . 3 . 3 遥感分析 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 附录 A 四阶 Runge-Kutta 计算方法–matlab 源程序 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 附录 B 避障段高层图处理–matlab 源程序. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 附录 C 动态规划求着陆地区–C++ 源代码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 附录 D 螺旋前进搜索着陆点算法–C++ 源代码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 3
    一、 问题重述 1 . 1 背景 实施在月球表面的软着陆是月球勘探计划的重要一步。所谓月球软着陆, 是指着陆 器在制动系统作用下以很小的速度准确降落到月面指定区域, 以保证试验设备和宇航员 的安全。由于月球表面没有大气，因此整个软着陆过程需要制导发动机的控制。正确地 建立着陆器的飞行动力学模型，并在此基础对着陆器的下降轨迹和制导律进行优化设 计，对于着陆器飞行程序的设计和燃料资源消耗等方面具有重要的指导意义。 1 . 2 需要解决的问题 根据题目信息和附件所示内容, 分析嫦娥三号软着陆过程中的 6 个阶段，研究以下 的问题： (1) 根据附件 1 与附件 2 研究嫦娥三号的着陆准备轨道，确定该椭圆轨道上近月点 与远月点的位置，以及嫦娥三号相应的速度大小与方向。 (2) 建立合理的着陆器飞行动力学方程，根据软着陆过程中 6 个阶段不同的特点与 要求，结合附件 1 与附件 2 的内容，确立嫦娥三号的下降轨迹和各个阶段的最优控制策 略。 (3) 根据问题一和问题二建立的数学模型，对模型进行相应的误差分析和敏感性分 析 二、 模型的假设 • 忽略月球因公转所产生的引力场不均匀; • 月球自转速度相对缓慢, 忽略自转影响与科里奥利力影响; • 忽略地球或其他行星对探测器吸引力的影响，只考虑月球对于飞行器的影响作用； • 因为月球的扁率仅为 1/963.725=0.00308，所以可以将月球简化为球体; • 因为月球表面没有大气层，几乎无空气阻力，嫦娥三号机械能守恒; • 嫦娥三号在软着陆全过程不发生意外碰撞和震荡. 4
    三、 符号说明 符号 意义 t0 t1 r0 r1 aL h0 h1 v0 v1 v0 vr0 v1 vr1 aF gm @ h h2 h3 th 嫦娥三号进行霍曼下降的初始时刻 嫦娥三号到达近月点的时刻 月球引力常数 远月点的月心距 近月点的月心距 月球半径 远月点轨道高度 近月点轨道高度 嫦娥三号在远月点的速度 嫦娥三号在近月点的速度 嫦娥三号在远月点的切向速度 嫦娥三号在远月点的径向速度 嫦娥三号在近月点的切向速度 嫦娥三号在近月点的径向速度 推力加速度大小 月球引力加速度大小 引力与重力方向的夹角 速度方向和水平方向的夹角 月面高度 粗避障段初始月面高度 粗避障段结束月面高度 避障段安全区方差阈值 5
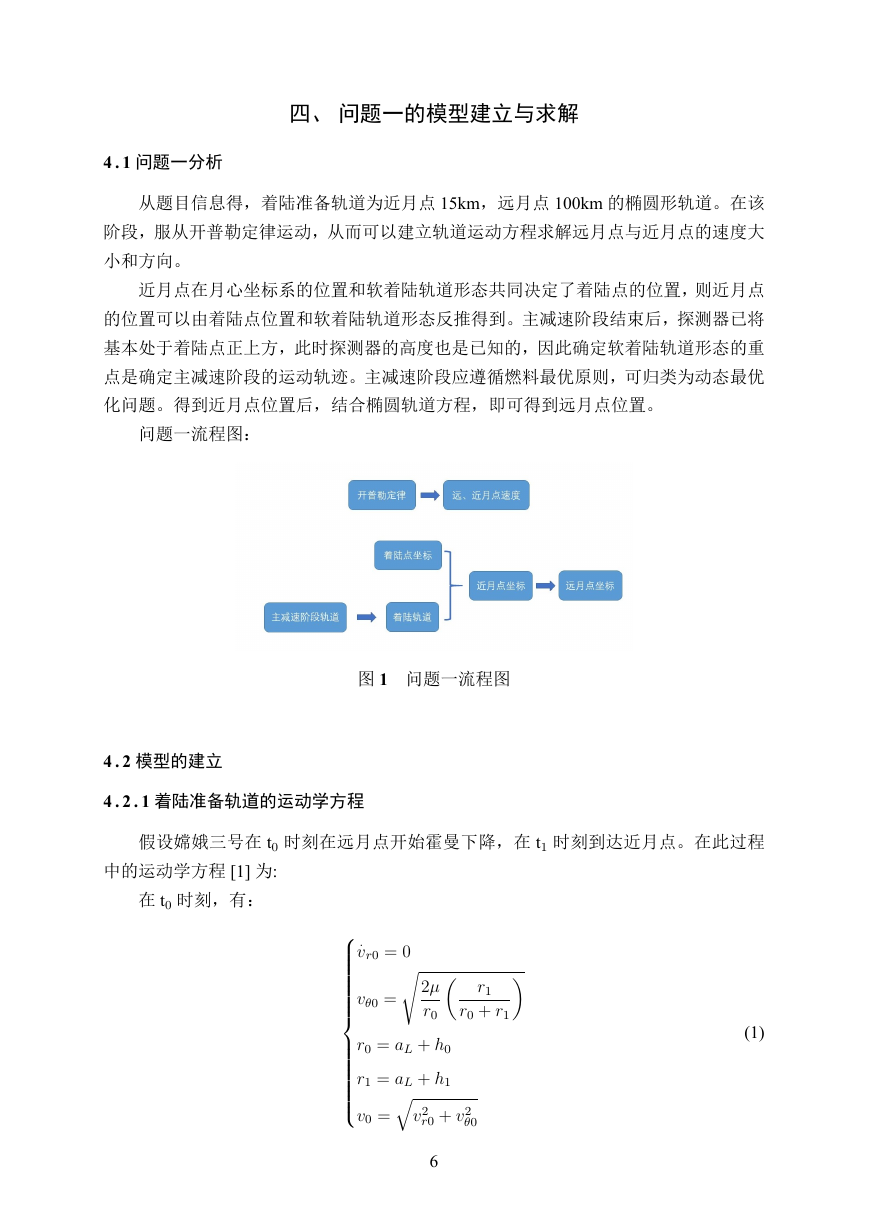
    四、 问题一的模型建立与求解 4 . 1 问题一分析 从题目信息得，着陆准备轨道为近月点 15km，远月点 100km 的椭圆形轨道。在该 阶段，服从开普勒定律运动，从而可以建立轨道运动方程求解远月点与近月点的速度大 小和方向。 近月点在月心坐标系的位置和软着陆轨道形态共同决定了着陆点的位置，则近月点 的位置可以由着陆点位置和软着陆轨道形态反推得到。主减速阶段结束后，探测器已将 基本处于着陆点正上方，此时探测器的高度也是已知的，因此确定软着陆轨道形态的重 点是确定主减速阶段的运动轨迹。主减速阶段应遵循燃料最优原则，可归类为动态最优 化问题。得到近月点位置后，结合椭圆轨道方程，即可得到远月点位置。 问题一流程图： 图 1 问题一流程图 4 . 2 模型的建立 4 . 2 . 1 着陆准备轨道的运动学方程 假设嫦娥三号在 t0 时刻在远月点开始霍曼下降，在 t1 时刻到达近月点。在此过程 中的运动学方程 [1] 为: 在 t0 时刻，有： √ : vr0 = 0 v0 = ) ( 2 r0 r1 r0 + r1 8>>>>>>>>>>>><>>>>>>>>>>>>: r0 = aL + h0 r1 = aL + h1 √ v0 = v2 r0 + v2 0 6 (1)
    分享到：
    赞 收藏

    相关推荐

    资料库

    信息化

    共收录1827份资料，累计6个分类，关注成员有19位，主要包括：管理软件,企业管理,电子商务,其它,IT管理,项目管理

    热门标签

    管理软件 企业管理 电子商务 其它 IT管理 项目管理

    最新资料