logo资料库

Information Theory, Inference, and Learning Algorithms(信息论、推理与学习....pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：11.13M 资料格式：pdf 举报 版权申诉
第1页 / 共640页
第2页 / 共640页
第3页 / 共640页
第4页 / 共640页
第5页 / 共640页
第6页 / 共640页
第7页 / 共640页
第8页 / 共640页
资料共640页，剩余部分请下载后查看
    Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Information Theory, Inference, and Learning Algorithms David J.C. MacKay
    Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Information Theory, Inference, and Learning Algorithms David J.C. MacKay mackay@mrao.cam.ac.uk c1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005 cCambridge University Press 2003 Version 7.2 (fourth printing) March 28, 2005 Please send feedback on this book via http://www.inference.phy.cam.ac.uk/mackay/itila/ Version 6.0 of this book was published by C.U.P. in September 2003. It will remain viewable on-screen on the above website, in postscript, djvu, and pdf formats. In the second printing (version 6.6) minor typos were corrected, and the book design was slightly altered to modify the placement of section numbers. In the third printing (version 7.0) minor typos were corrected, and chapter 8 was renamed ‘Dependent random variables’ (instead of ‘Correlated’). In the fourth printing (version 7.2) minor typos were corrected. (C.U.P. replace this page with their own page ii.)
    Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Contents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Preface Introduction to Information Theory . . . . . . . . . . . . . Probability, Entropy, and Inference . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 2 3 More about Inference I Data Compression . . . . . . . . . . . . . . . . . . . . . . 4 5 6 7 The Source Coding Theorem . . . . . . . . . . . . . . . . . Symbol Codes . . . . . . . . . . . . . . . . . . . . . . . . . Stream Codes . . . . . . . . . . . . . . . . . . . . . . . . . . Codes for Integers . . . . . . . . . . . . . . . . . . . . . . . v 3 22 48 65 67 91 110 132 II Noisy-Channel Coding . . . . . . . . . . . . . . . . . . . . 137 Dependent Random Variables . . . . . . . . . . . . . . . . . 8 Communication over a Noisy Channel . . . . . . . . . . . . 9 10 The Noisy-Channel Coding Theorem . . . . . . . . . . . . . 11 Error-Correcting Codes and Real Channels . . . . . . . . . 138 146 162 177 III Further Topics in Information Theory . . . . . . . . . . . . . 191 12 Hash Codes: Codes for Ecient Information Retrieval 13 Binary Codes 14 Very Good Linear Codes Exist 15 Further Exercises on Information Theory 16 Message Passing 17 Communication over Constrained Noiseless Channels 18 Crosswords and Codebreaking 19 Why have Sex? Information Acquisition and Evolution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193 206 229 233 241 248 260 269 IV Probabilities and Inference . . . . . . . . . . . . . . . . . . 281 . . . . . . . . . . . 20 An Example Inference Task: Clustering 21 Exact Inference by Complete Enumeration . . . . . . . . . 22 Maximum Likelihood and Clustering . . . . . . . . . . . . . 23 Useful Probability Distributions . . . . . . . . . . . . . . . 24 Exact Marginalization . . . . . . . . . . . . . . . . . . . . . 25 Exact Marginalization in Trellises . . . . . . . . . . . . . . 26 Exact Marginalization in Graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 Laplace’s Method 284 293 300 311 319 324 334 341
    Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Ising Models . . . . . . . . . . . 28 Model Comparison and Occam’s Razor . . . . . . . . . . . . . . . . . . . . . 29 Monte Carlo Methods . . . . . . . . . . . . . . . . 30 Ecient Monte Carlo Methods 31 . . . . . . . . . . . . . . . . . . . . . . . . . . 32 Exact Monte Carlo Sampling . . . . . . . . . . . . . . . . . 33 Variational Methods . . . . . . . . . . . . . . . . . . . . . . 34 Independent Component Analysis and Latent Variable Mod- elling 343 357 387 400 413 422 437 445 451 457 35 Random Inference Topics 36 Decision Theory 37 Bayesian Inference and Sampling Theory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . V Neural networks . . . . . . . . . . . . . . . . . . . . . . . . 467 Introduction to Neural Networks 38 . . . . . . . . . . . . . . . 39 The Single Neuron as a Classier . . . . . . . . . . . . . . . 40 Capacity of a Single Neuron . . . . . . . . . . . . . . . . . . 41 Learning as Inference . . . . . . . . . . . . . . . . . . . . . 42 Hopeld Networks . . . . . . . . . . . . . . . . . . . . . . . 43 Boltzmann Machines . . . . . . . . . . . . . . . . . . . . . . 44 Supervised Learning in Multilayer Networks . . . . . . . . . 45 Gaussian Processes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 Deconvolution 468 471 483 492 505 522 527 535 549 VI Sparse Graph Codes . . . . . . . . . . . . . . . . . . . . . 555 47 Low-Density Parity-Check Codes . . . . . . . . . . . . . . 48 Convolutional Codes and Turbo Codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49 Repeat{Accumulate Codes 50 Digital Fountain Codes . . . . . . . . . . . . . . . . . . . . 557 574 582 589 VII Appendices . . . . . . . . . . . . . . . . . . . . . . . . . . 597 . . . . . . . . . . . . . . . . . . . . . . . . . . . . A Notation . . . . . . . . . . . . . . . . . . . . . . . . . . B Some Physics C Some Mathematics . . . . . . . . . . . . . . . . . . . . . . . Bibliography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Index . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 598 601 605 613 620
    Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Preface This book is aimed at senior undergraduates and graduate students in Engi- neering, Science, Mathematics, and Computing. It expects familiarity with calculus, probability theory, and linear algebra as taught in a rst- or second- year undergraduate course on mathematics for scientists and engineers. Conventional courses on information theory cover not only the beauti- ful theoretical ideas of Shannon, but also practical solutions to communica- tion problems. This book goes further, bringing in Bayesian data modelling, Monte Carlo methods, variational methods, clustering algorithms, and neural networks. Why unify information theory and machine learning? Because they are two sides of the same coin. In the 1960s, a single eld, cybernetics, was populated by information theorists, computer scientists, and neuroscientists, all studying common problems. Information theory and machine learning still belong together. Brains are the ultimate compression and communication systems. And the state-of-the-art algorithms for both data compression and error-correcting codes use the same tools as machine learning. 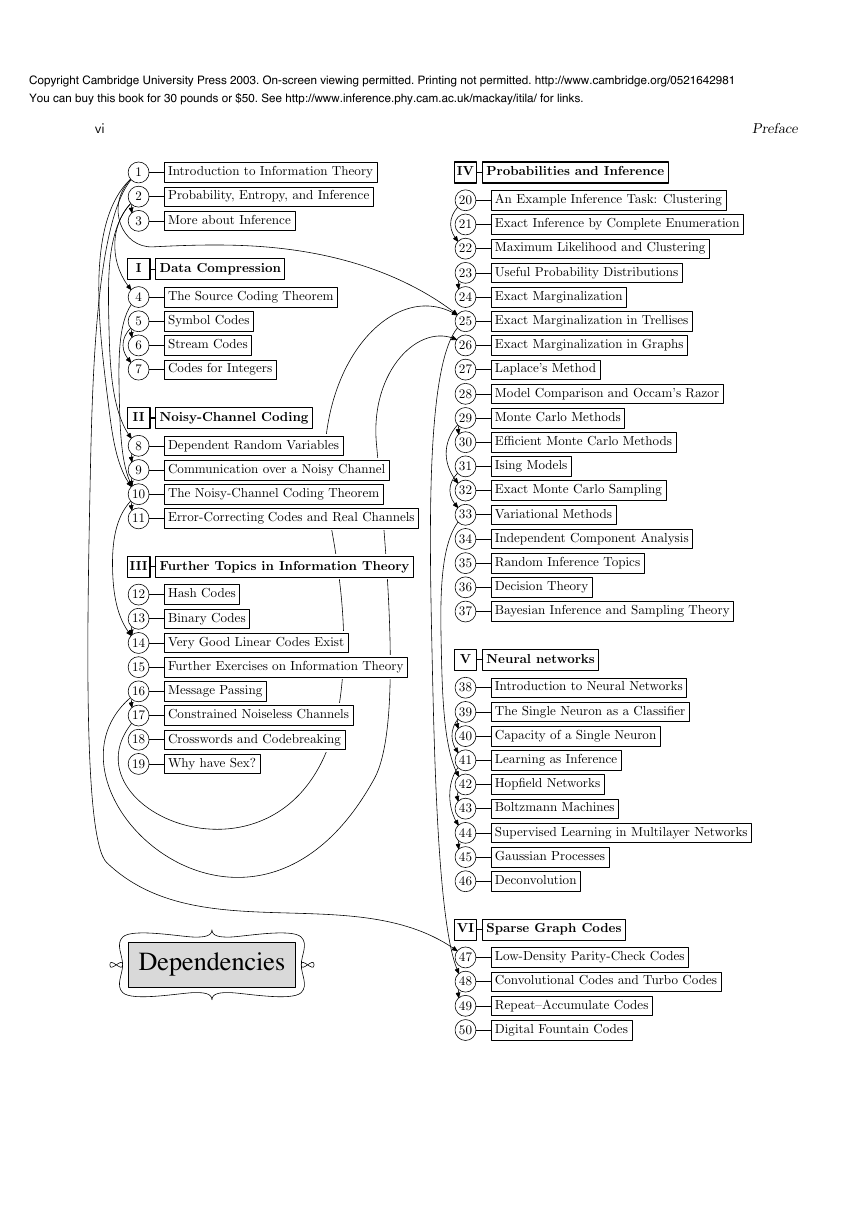How to use this book The essential dependencies between chapters are indicated in the gure on the next page. An arrow from one chapter to another indicates that the second chapter requires some of the rst. Within Parts I, II, IV, and V of this book, chapters on advanced or optional topics are towards the end. All chapters of Part III are optional on a rst reading, except perhaps for Chapter 16 (Message Passing). The same system sometimes applies within a chapter: the nal sections of- ten deal with advanced topics that can be skipped on a rst reading. For exam- ple in two key chapters { Chapter 4 (The Source Coding Theorem) and Chap- ter 10 (The Noisy-Channel Coding Theorem) { the rst-time reader should detour at section 4.5 and section 10.4 respectively. Pages vii{x show a few ways to use this book. First, I give the roadmap for a course that I teach in Cambridge: ‘Information theory, pattern recognition, and neural networks’. The book is also intended as a textbook for traditional courses in information theory. The second roadmap shows the chapters for an introductory information theory course and the third for a course aimed at an understanding of state-of-the-art error-correcting codes. The fourth roadmap shows how to use the text in a conventional course on machine learning. v
    vi 1 2 3 Probability, Entropy, and Inference More about Inference I Data Compression 4 5 6 7 The Source Coding Theorem Symbol Codes Stream Codes Codes for Integers 8 9 10 11 Dependent Random Variables Communication over a Noisy Channel The Noisy-Channel Coding Theorem Error-Correcting Codes and Real Channels III Further Topics in Information Theory Hash Codes Binary Codes 12 13 14 15 20 21 An Example Inference Task: Clustering Exact Inference by Complete Enumeration 22 Maximum Likelihood and Clustering 23 24 25 26 27 Useful Probability Distributions Exact Marginalization Exact Marginalization in Trellises Exact Marginalization in Graphs Laplace’s Method 28 Model Comparison and Occam’s Razor 30 31 32 33 34 35 36 37 Ecient Monte Carlo Methods Ising Models Exact Monte Carlo Sampling Variational Methods Independent Component Analysis Random Inference Topics Decision Theory Bayesian Inference and Sampling Theory Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Introduction to Information Theory IV Probabilities and Inference Preface II Noisy-Channel Coding 29 Monte Carlo Methods Very Good Linear Codes Exist Further Exercises on Information Theory V Neural networks 16 Message Passing 17 18 Constrained Noiseless Channels Crosswords and Codebreaking 19 Why have Sex? Dependencies 38 39 40 41 42 43 44 45 46 Introduction to Neural Networks The Single Neuron as a Classier Capacity of a Single Neuron Learning as Inference Hopeld Networks Boltzmann Machines Supervised Learning in Multilayer Networks Gaussian Processes Deconvolution VI Sparse Graph Codes 47 48 49 50 Low-Density Parity-Check Codes Convolutional Codes and Turbo Codes Repeat{Accumulate Codes Digital Fountain Codes
    Preface 1 1 2 2 3 3 Probability, Entropy, and Inference Probability, Entropy, and Inference More about Inference More about Inference I Data Compression 4 4 5 5 6 6 7 The Source Coding Theorem The Source Coding Theorem Symbol Codes Symbol Codes Stream Codes Stream Codes Codes for Integers 8 8 9 9 10 10 11 11 Dependent Random Variables Dependent Random Variables Communication over a Noisy Channel Communication over a Noisy Channel The Noisy-Channel Coding Theorem The Noisy-Channel Coding Theorem Error-Correcting Codes and Real Channels Error-Correcting Codes and Real Channels III Further Topics in Information Theory Hash Codes Binary Codes 12 13 14 15 20 20 21 21 An Example Inference Task: Clustering An Example Inference Task: Clustering Exact Inference by Complete Enumeration Exact Inference by Complete Enumeration 22 Maximum Likelihood and Clustering 22 Maximum Likelihood and Clustering 23 24 24 25 26 27 27 Useful Probability Distributions Exact Marginalization Exact Marginalization Exact Marginalization in Trellises Exact Marginalization in Graphs Laplace’s Method Laplace’s Method 28 Model Comparison and Occam’s Razor 30 30 31 31 32 32 33 33 34 35 36 37 Ecient Monte Carlo Methods Ecient Monte Carlo Methods Ising Models Ising Models Exact Monte Carlo Sampling Exact Monte Carlo Sampling Variational Methods Variational Methods Independent Component Analysis Random Inference Topics Decision Theory Bayesian Inference and Sampling Theory Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Introduction to Information Theory Introduction to Information Theory IV Probabilities and Inference vii II Noisy-Channel Coding 29 Monte Carlo Methods 29 Monte Carlo Methods Very Good Linear Codes Exist Further Exercises on Information Theory V Neural networks 16 Message Passing 17 18 Constrained Noiseless Channels Crosswords and Codebreaking 19 Why have Sex? My Cambridge Course on, Information Theory, Pattern Recognition, and Neural Networks 38 38 39 39 40 40 41 41 42 42 43 44 45 46 Introduction to Neural Networks Introduction to Neural Networks The Single Neuron as a Classier The Single Neuron as a Classier Capacity of a Single Neuron Capacity of a Single Neuron Learning as Inference Learning as Inference Hopeld Networks Hopeld Networks Boltzmann Machines Supervised Learning in Multilayer Networks Gaussian Processes Deconvolution VI Sparse Graph Codes 47 47 48 49 50 Low-Density Parity-Check Codes Low-Density Parity-Check Codes Convolutional Codes and Turbo Codes Repeat{Accumulate Codes Digital Fountain Codes
    viii 1 1 2 2 3 Probability, Entropy, and Inference Probability, Entropy, and Inference More about Inference I Data Compression 4 4 5 5 6 6 7 The Source Coding Theorem The Source Coding Theorem Symbol Codes Symbol Codes Stream Codes Stream Codes Codes for Integers 8 8 9 9 10 10 11 Dependent Random Variables Dependent Random Variables Communication over a Noisy Channel Communication over a Noisy Channel The Noisy-Channel Coding Theorem The Noisy-Channel Coding Theorem Error-Correcting Codes and Real Channels III Further Topics in Information Theory Hash Codes Binary Codes 12 13 14 15 20 21 An Example Inference Task: Clustering Exact Inference by Complete Enumeration 22 Maximum Likelihood and Clustering 23 24 25 26 27 Useful Probability Distributions Exact Marginalization Exact Marginalization in Trellises Exact Marginalization in Graphs Laplace’s Method 28 Model Comparison and Occam’s Razor 30 31 32 33 34 35 36 37 Ecient Monte Carlo Methods Ising Models Exact Monte Carlo Sampling Variational Methods Independent Component Analysis Random Inference Topics Decision Theory Bayesian Inference and Sampling Theory Copyright Cambridge University Press 2003. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/0521642981 You can buy this book for 30 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/ for links. Introduction to Information Theory Introduction to Information Theory IV Probabilities and Inference Preface II Noisy-Channel Coding 29 Monte Carlo Methods Very Good Linear Codes Exist Further Exercises on Information Theory V Neural networks 16 Message Passing 17 18 Constrained Noiseless Channels Crosswords and Codebreaking 19 Why have Sex? Short Course on Information Theory 38 39 40 41 42 43 44 45 46 Introduction to Neural Networks The Single Neuron as a Classier Capacity of a Single Neuron Learning as Inference Hopeld Networks Boltzmann Machines Supervised Learning in Multilayer Networks Gaussian Processes Deconvolution VI Sparse Graph Codes 47 48 49 50 Low-Density Parity-Check Codes Convolutional Codes and Turbo Codes Repeat{Accumulate Codes Digital Fountain Codes
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料