Matlab中常微分方程数值解法（ode45函数）.pdf-资料库

u011753051-5982035-16359647267772209929.pdf-第1页.png

第1页 / 共21页

u011753051-5982035-16359647267772209929.pdf-第2页.png

第2页 / 共21页

u011753051-5982035-16359647267772209929.pdf-第3页.png

第3页 / 共21页

u011753051-5982035-16359647267772209929.pdf-第4页.png

第4页 / 共21页

u011753051-5982035-16359647267772209929.pdf-第5页.png

第5页 / 共21页

u011753051-5982035-16359647267772209929.pdf-第6页.png

第6页 / 共21页

u011753051-5982035-16359647267772209929.pdf-第7页.png

第7页 / 共21页

u011753051-5982035-16359647267772209929.pdf-第8页.png

第8页 / 共21页

http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! Matlab 中常微分方程数值解法讲解© 作者：dynamic 时间：2008.12.10 版权：All Rights Reserved By www.matlabsky.cn ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★ Matlab Sky 联盟----打造最优秀、专业和权威的 Matlab 技术交流平台! 网址：http://www.matlabsky.cn /com/org/net 邮箱：matlabsky@gmail.com QQ 群：23830382 40510634 16233891(满了) 44851559(满了) 论坛拥有 40 多个专业版块，内容涉及资料下载、视频教学、数学建模、数学运算、程序设计、GUI 开发、simulink 仿真、统计概率、拟合优化、扩展编程、算法研究、控制系统、信号通信、图像处理、经济金融、生物化学、航空航天、人工智能、汽车设计、机械自动化、毕业设计等几十个方面! 请相信我们：1.拥有绝对优秀的技术人员，热情的版主，严谨负责的管理团队 2.免费提供技术交流和在线解答 ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★ 1

http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! 1.ODE解算器简介 ............................................................................................................................................................... 3 2.微分方程转换 .................................................................................................................................................................... 5 3.刚性/非刚性问题 .............................................................................................................................................................. 8 4.隐式微分方程(IDE) ........................................................................................................................................................ 10 5.微分代数方程(DAE) ....................................................................................................................................................... 15 6.延迟微分方程(DDE) ....................................................................................................................................................... 18 7.边值问题(BVP) ............................................................................................................................................................... 20 2

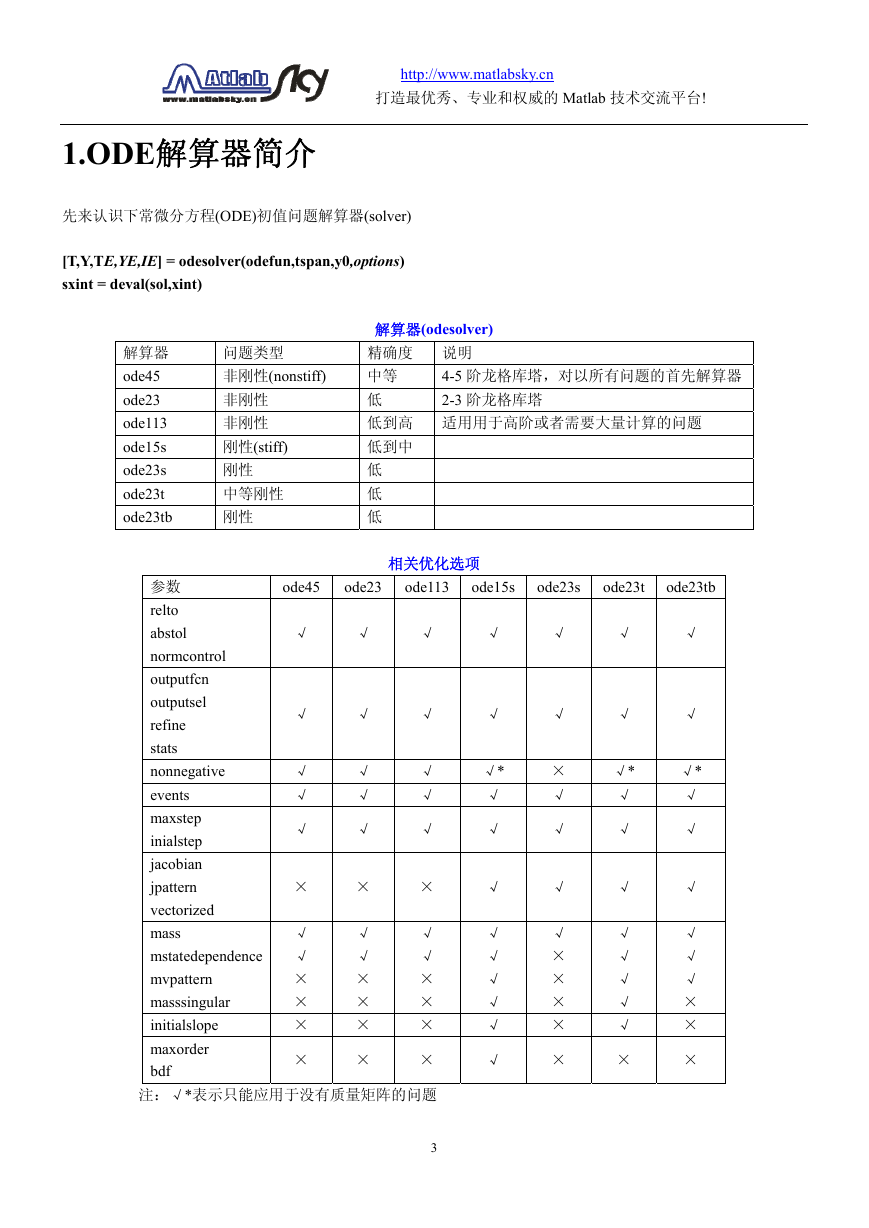
http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! 1.ODE解算器简介先来认识下常微分方程(ODE)初值问题解算器(solver) [T,Y,TE,YE,IE] = odesolver(odefun,tspan,y0,options) sxint = deval(sol,xint) 解算器 ode45 ode23 ode113 ode15s ode23s ode23t ode23tb 问题类型非刚性(nonstiff) 非刚性非刚性刚性(stiff) 刚性中等刚性刚性 4-5 阶龙格库塔，对以所有问题的首先解算器 2-3 阶龙格库塔解算器(odesolver) 精确度说明中等低低到高适用用于高阶或者需要大量计算的问题低到中低低低参数 relto abstol normcontrol outputfcn outputsel refine stats nonnegative events maxstep inialstep jacobian jpattern vectorized mass mstatedependence mvpattern masssingular initialslope maxorder bdf 相关优化选项 ode45 ode23 ode113 ode15s ode23s ode23t ode23tb √ √ √ √ √ √ √ √ √ √ √ × √ √ × × × × √ √ √ √ × √ √ × × × × √ √ √ √ × √ √ × × × × √ √* √ √ √ √ √ √ √ √ √ √ × √ √ √ √ × × × × × √ √ √* √ √ √ √ √ √ √ √ × √* √ √ √ √ √ √ × × × 注：√*表示只能应用于没有质量矩阵的问题 3

http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! 输入参数： odefun：微分方程的句柄，必须写成 Matlab 规范格式，这个具体在后面讲解 tspab=[t0 tf]或者[t0,t1,…tf]：微分变量的范围，两者都是根据 t0 和 tf 的值自动选择步长，后只是前者返回所有计算点的微分值，而后者只返回指定的点的微分值，一定要注意对于后者 tspan 必须严格单调，还有就是两者数据存储时使用的内存不同(明显前者多)，其它没有任何本质的区别 y0=[y(0),y’(0),y’’(0)…]：微分方程初值，依次输入所有状态变量的初值 options：微分优化参数，是一个结构体，使用 odeset 可以设置具体参数，详细内容查看帮助输出参数： T：时间列向量 Y：二维数组，第 i 列表示第 i 个状态变量的值，行数与 T 一致在求解 ODE 时，我们还会用到 deval()函数，deval 的作用就是通过结构体 solution 计算 t 对应 x 值，和 polyval 之类的很相似输入参数： sol：就是上次调用 ode**函数得道的结构体解 xint：需要计算的点，可以是标量或者向量，但是必须在 tspan 范围内该函数的好处就是如果我想知道 t=t0 时的 y 值，不需要重新使用 ode 计算，而直接使用上次计算的得道 solution 就可以 4

http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! 2.微分方程转换好，上面我们把 Matlab 中的常微分方程(ODE)的解算器讲解的差不多了，下面我们就具体开始介绍如何使用上面的知识吧！现实总是残酷的，要得到就必须先付出，不可能所有的 ODE 一拿来就可以直接使用，因此，在使用 ODE 解算器之前，我们需要做的第一步，也是最重要的一步就是将微分方程组化成 Matlab 可接受的标准形式！如果 ODEs 由一个或多个高阶微分方程给出，则我们应先将其变换成一阶显式常微分方程组！下面我们以两个高阶微分方程构成的 ODEs 为例介绍如何将之变换成一个一阶显式常微分方程组。 step1.将微分方程的最高阶变量移到等式的左边，其他移到右边，并按阶次从低到高排列，假如说两个高阶微分方程最后能够显式的表达成如下所示： y ', , ⎧ ⎪ ⎨ y , ', ( ⎪⎩ 然而现实总是残酷的，有时方程偏偏是隐式的，没法写成上面的样子，不用担心 Matlab 早就为我们想到了，这个留在后面的隐式微分方程数值求解中再详细讲解！ step2.为每一阶微分式选择状态变量，最高阶除外 f t x x x '', , ( , ', g t x x x , ( , '', ', y y , y y , x x ( = = x y ) ) , , , , n ( ) 1) − 1) − 1) − 1) − m m m n n ( ( ( ) ( ( 2 n + m , 1 + 1 + 1) − 1) − x y x = = '', ', = x m n + x x m , = x = 3 y ', x = m y '', x x , = 2 y x , = m x 1 x m 从上面的变换，我们注意到，ODEs中所有因变量的最高阶次之和就是需要的状态变量的个数，最高阶的微分式(比如上面的x-(m)和y(n))不需要给它一个状态变量 step3.根据上面选用的状态变量，写出所有状态变量的一阶微分的表达式 5

http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! x 2 x 3 x 4 x x x ' 1 ' ' 3 2 = = = = m x x ' ' m 1 + f = , , x m + n ) 1 , t x x x ( , , 3 x m 2 + 2 x ' m n + = g t x x x ( , , 3 , 1 2 , , x m n + ) 注意到，最高阶次的微分式的表达式直接就是 step1 中的微分方程好，到此为止，一阶显式常微分方程组，变化顺利结束，接下来就是 Matlab 编程了。请记住上面的变化很重要， Matla 中所有微分方程的求解都需要上面的变换下面通过一个实例演示 ODEs 的转换和求解已知 ⎧ ⎪ ⎪ ⎨ ⎪ ⎪⎩ 其中： x r ( = + 1 x (0) 1.2, = x y ) ( , 满足下面的微分方程组 x ( − r 3 2 x + r 3 1 y y * μ μ r r 3 3 2 1 x ) * 2 − = μ y (0) 0, '(0) 1 = − , , 1.04935751 r , ) μ 2 x y '(0) 0, y = * μ μ μ μ 卫星的运动轨迹 1/ 82.45 y + = − y '' 2 ' = = μμ Apoll + − y + − x x 2 ' = − ( = * μ y '' * ( 2 + − ) − x ) 2 2 【解】真是万幸，该 ODEs 已经帮我们完成了 step1，我们只需要完成 step2 和 step3 了 (1)选择一组状态变量 x 1 x x , 2 x 3 = = = x ', y x , 4 = y ' (2)写出所有状态变量的一阶微分表达式 6

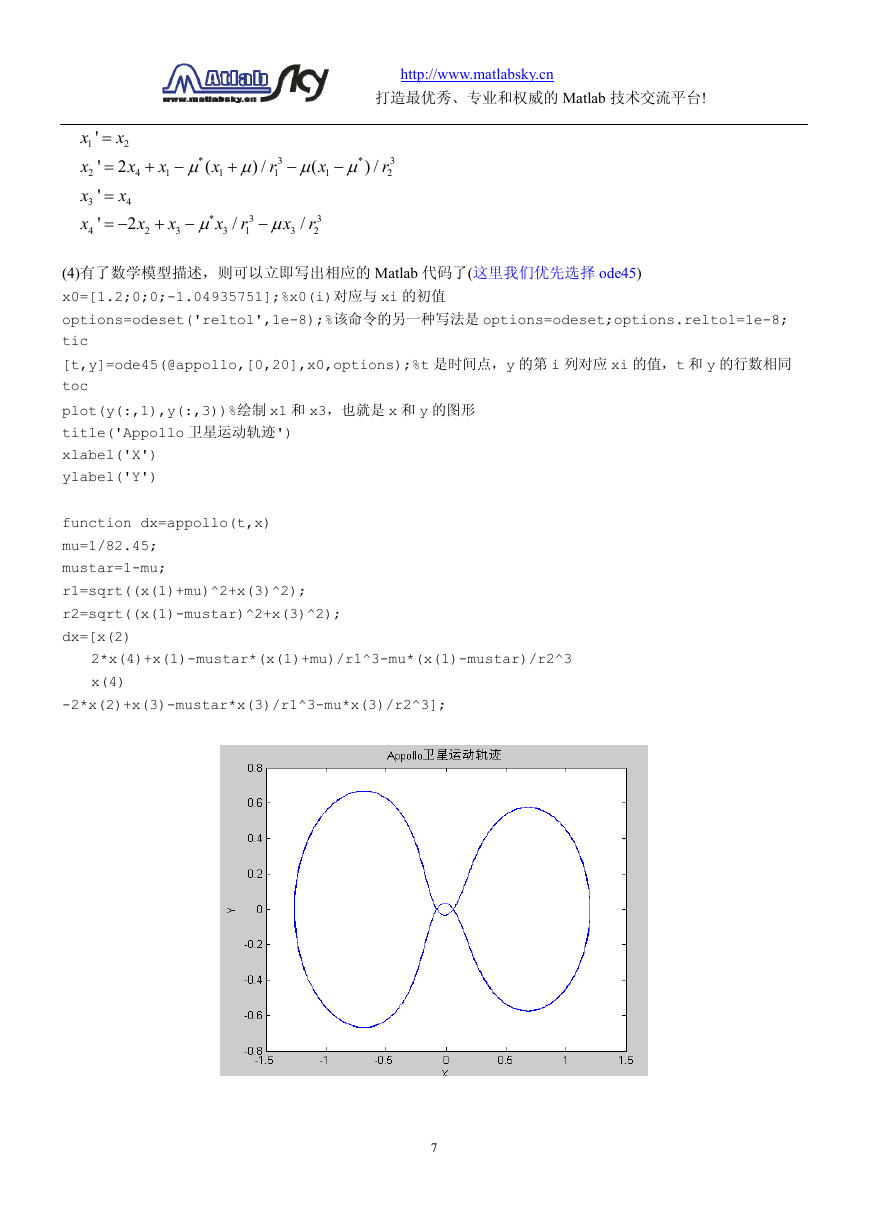
http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! + x 1 − * μ ( x 1 + ) / μ r 3 1 − * μ μ − ( x 1 ) / r 3 2 x 1 x 2 x 3 x 4 x ' = 2 x ' 2 = 4 x ' = 4 2 ' = − x 2 + x 3 − * μ x 3 / r 3 1 − x μ 3 / r 3 2 (4)有了数学模型描述，则可以立即写出相应的 Matlab 代码了(这里我们优先选择 ode45) x0=[1.2;0;0;-1.04935751];%x0(i)对应与 xi 的初值 options=odeset('reltol',1e-8);%该命令的另一种写法是 options=odeset;options.reltol=1e-8; tic [t,y]=ode45(@appollo,[0,20],x0,options);%t 是时间点，y 的第 i 列对应 xi 的值，t 和 y 的行数相同 toc plot(y(:,1),y(:,3))%绘制 x1 和 x3，也就是 x 和 y 的图形 title('Appollo 卫星运动轨迹') xlabel('X') ylabel('Y') function dx=appollo(t,x) mu=1/82.45; mustar=1-mu; r1=sqrt((x(1)+mu)^2+x(3)^2); r2=sqrt((x(1)-mustar)^2+x(3)^2); dx=[x(2) 2*x(4)+x(1)-mustar*(x(1)+mu)/r1^3-mu*(x(1)-mustar)/r2^3 x(4) -2*x(2)+x(3)-mustar*x(3)/r1^3-mu*x(3)/r2^3]; 7

http://www.matlabsky.cn 打造最优秀、专业和权威的 Matlab 技术交流平台! 3.刚性/非刚性问题在工程实践中，我们经常遇到一些 ODEs，其中某些解变换缓慢，另一些变化很快，且相差悬殊的微分方程，这就是所谓的刚性问题(Stiff)，对于所有解的变化相当我们则称为非刚性问题(Nonstiff)。对于刚性问题一般不适合使用 ode45 这类函数求解。由于非刚性问题我们使用的多比较多，我们就不多说，下面主要讲解下 Stiff 看一个例子，考虑下面的微分方程 2 − 10000 y ' 0.04(1 ⎧ = ⎪ 1 ⎨ y ' = − ⎪⎩ 其中 y (0) = y 1 y 1 y y ) (1 ) − − 2 1 y 3000(1 − + + ) 2 0.0001(1 2 − y 2 2 ) 2 y 1 (0) 1 = t ∈ [0,100] 【解】题目中已经帮我们完成了方程组转换，下面我们就直接编程了 (1)编写微分方程函数 odefun=@(t,x)[0.04*(1-x(1))-(1-x(2))*x(1)+0.0001*(1-x(2))^2 -1e4*x(1)+3000*(1-x(2))^2]; x0=[0 1]; tspan=[0 100]; options=odeset('reltol',1e-6,'abstol',1e-8); (2)使用 ode45 函数计算(反正我们是没有信心等待它，太慢了) tic;[t,y]=ode45(odefun,tspan,x0,options);toc disp(['ode45 计算的点数' num2str(length(t))]) (3)使用 ode15s 函数计算 tic;[t2,y2]=ode15s(odefun,tspan,x0,options);toc disp(['ode15s 计算的点数' num2str(length(t2))]) (4)绘图看看 figure('numbertitle','off','name','Stiff ODEs Demo—by Matlabsky') subplot(121) title('Using ode45') plot(t,y) subplot(122) plot(t2,y2) title('Using ode15s') 8

资料库

Matlab中常微分方程数值解法（ode45函数）.pdf

相关推荐

课程资源

热门标签

最新资料