预应力锚索的锚固机理与锚固效应影响因素的数值仿真试验 .pdf

发布时间：2022-06-14 发布人：admin 分类：说明书资料大小：0.60M 资料格式：pdf 举报版权申诉

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第1页.png

第1页 / 共10页

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第2页.png

第2页 / 共10页

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第3页.png

第3页 / 共10页

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第4页.png

第4页 / 共10页

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第5页.png

第5页 / 共10页

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第6页.png

第6页 / 共10页

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第7页.png

第7页 / 共10页

b1534922-f2e4-47ff-98bf-eea4699f8b5d.pdf-第8页.png

第8页 / 共10页

文本预览

中国科技论文在线 http://www.paper.edu.cn 预应力锚索的锚固机理与锚固效应影响因素的数值仿真试验1 张森 1,2，言志信*1,2，张学东 1,2，曹小红 1,2 1 兰州大学土木工程与力学学院，兰州 (730000) 2 西部灾害与环境力学教育部重点实验室，兰州 (730000) E-mail: zhangsen04@lzu.cn 摘要：本文采用连续介质快速拉格朗日计算程序，从荷载传递及锚固机理入手，且将传统的整体式锚固系统做锚杆体-砂浆-围岩分离式考虑，建立锚固系统各种破坏形式和判断方程。通过数值仿真试验模拟预应力、锚固段长度、锚索刚度、岩土体性质等对锚固效果的影响，并由拉拔试验动态模拟锚固系统的破坏过程，将所得结果和已有研究成果相比较，得出更严密准确的结论，为工程实际应用提供可靠的参考意见并指出下一步研究方向。关键词：预应力锚索；岩土工程；锚固系统；锚固机理；影响因素；中图分类号：TU452 前言随着岩土锚固技术应用的日趋广泛，岩土工程界通过物理模型试验、数值仿真模拟，现场观测试验等手段，研究锚索的锚固机理和锚索锚固段应力分布，例如加拿大的 Phillips[1] 用幂函数，蒋忠信[2]构造正态分布函数、张季如[3]用双曲函数、肖世国[4]和尤春安[5]用指数函数，朱玉[6]等用复合幂函数来描述锚固段剪应力分布曲线，也讨论锚固段的长度及其安全储备等。但是由于岩土工程自身的复杂性，影响锚固效果的因素众多，当前对岩土锚固技术的研究也存在着不少问题，主要有：理论研究仍然滞后于工程应用的需要；锚固体力的传递及应力的分布规律仅能定性的描述；在实际应用中大多采用粘结应力均匀分布的理想形式进行工程设计；对锚索加固机理没有统一的认识，缺乏行之有效的合理计算方法等[7]。随着李宁[8]提出“岩土工程数值仿真试验”的概念和思路，人们利用各种数值模拟软件对预应力锚索现场加载与破坏进行了大量研究。然而，现在许多数值模拟程序在其理论和所采用的算法上都或多或少存在缺陷[9]，例如有限元和边界元都是基于小变形的假设所提出的，而且运行需要大量的内存；国内所使用的离散元程序一般都是假定离散块体为刚体，本身不发生变形。本文用的连续介质快速拉格朗日程序，因其较好的吸取了上述方法的优点并准确模拟和全面表述岩土体锚固效果及其影响因素而在岩土工程领域得到了广泛的应用。总之，虽然国内外对预应力锚索锚固机理做了些研究，但对锚索的锚固机理和力学模型、锚固效果的影响因素及锚固的破坏形式等综合、系统分析比较少。本文采用连续介质快速拉格朗日计算程序，通过数值仿真试验方法，且将传统的整体式锚固系统做锚杆体-砂浆-围岩分离式考虑，从荷载传递及锚固机理入手，建立锚固系统各种破坏形式和判断方程，通过数值仿真试验方法模拟预应力、锚固段长度、锚索刚度、岩土体性质等对锚固效果的影响，并由通过拉拔试验动态模拟锚索的破坏过程，并将所得结果和已有成果相比较，最后给出结论并指出下一步研究方向。 1基金项目：高等学校博士学科点专项科研基金项目（20090211110016）、甘肃省科技计划资助项目（096RJZA048） -1-

中国科技论文在线 http://www.paper.edu.cn 1 锚索的荷载传递及锚固机理国内外应用最广的拉力型锚索的传力方式是荷载通过粘着力、机械连锁和摩擦力形式从锚索转移到灌浆体上，经由灌浆体传递到围岩。在整个锚固系统中包括三相两界面见图 1, 在采用 FLAC 计算时将该系统简化的力学模型见图 2。从受力分析来看，拉力型锚索依靠锚固段的不均匀拉伸来带动与锚固段结合的岩土体变形，以此来调节岩土体的抗剪强度[10,11]。锚索轴力与砂浆剪力是一对平衡力，任取锚索一微段，如图 3 所示，其两个截面上的轴力差就应该等于该微段上所有节点上的剪力之和，根据静力平衡有：图 1 锚固系统分离式物理模型图 2 基于浆体材料锚固段剪切强度的锚索力学模型锚索 τ 图 3 锚索轴力与剪应力关系 N πτ 2 r dx πτ + 2 r dx 即 d = − N （1） d + N N = 式中： N 为锚索轴力 r 为锚索半径 τ为砂浆剪应力从(1)式可以看出，剪力与轴力的增量呈负相关，若剪力增大较快则锚索的轴力减小越快，从后面的数值模拟计算中也可以看出。 2 锚固系统破坏的形式及数值模拟判断方式采用 FLAC2D6.0 程序进行数值模拟，它能形象地模拟出锚固机理。安装了预应力锚索的锚固系统包含锚索和锚孔中的灌注水泥浆（砂浆）几部分介质（图 1），而对锚索加固机理的数值仿真，最重要的是要正确模拟锚固体的各组成部分之间的界面及其介质破坏形式。在 FALC 软件里，锚索采用 cable 单元来模拟，其轴向刚度 K 可以通过 K = 得到， EA L 其中 E 为锚索单元的弹性模量，A 为锚索的横截面积，L 为锚索单元长度。锚索与周围岩石的接触具有粘结性和自然摩擦，在理想情况下（图 2 所示），节点轴向上采用弹簧-滑块来描述，当锚索－浆体界面和浆体－岩体界面之间产生相对位移时，灌浆环的剪切特性即可通过下列参数来进行数值描述：浆体的剪切刚度 Kbond ，浆体的粘结强度 Sbond ，浆体的摩擦角 S friction ，灌浆体的外围周长 Pg 和有效围压 mσ 。灌浆锚索系统的力学特性必须服从图 -2-

中国科技论文在线 4 所示的准则[11]。 http://www.paper.edu.cn 相对剪切位移（压力）（张力）水泥浆剪切强度准则 σm 水泥浆剪切力-位移关系图 4 Cable 单元的水泥浆材料强度破坏形式杆体的断裂砂浆体的压碎表 1 锚固系统破坏形式与数值判断方式数值模拟判断方式当 cable 轴力大于其赋予的拉伸\压缩强度时，显示锚索单元破砂浆能承受的最大剪力根据图 4 的强度准则判断坏沿着锚索与砂浆体的结合处破坏忽略摩擦力时该界面最大粘结力为： Dπ τ peak 沿着砂浆体与地层结合处破坏忽略摩擦力时该界面最大粘结力为： Dπ （ +2 ） t τ peak 地层岩土体破坏根据摩尔库伦准则判断 -为岩体和灌浆体单轴抗压强度中较小一个的一半注： D -锚索直径 t -灌浆厚度 peakτ 3 预应力锚索锚固机理的数值模拟分析 3.1 计算模型、边界条件及模拟方法计算模型沿 x,y 方向计算范围为 20m×20m,锚索所处的地方单元密度最大,网格生成如图 5,为了合理地面板模拟,采用 FLAC 自带的 liner 单元来模拟,预应力锚索不同于普通锚杆的加固机制在于对加固体应力场及加固体刚度的影响,特别被加固体较大时,锚索对加固体刚度贡献就大于应力贡献。为了研究锚索的加固机理,所以在模拟模型中对应力边界条件进行了一定的简化,模型中除了面板作用的侧面为自由面外，其余面法向约束，且不考虑其他外因的影响，同时也忽略介质的重力作用。图 5 计算模型与网格划分以前的常规算法通常是通过程序关键字 tens 指定预应力的大小，但由于该初始值无对应的外力与之平衡，因此必然会因为计算导致预应力损失，文中程序为了避免这种情况出现，采用一种施加方向相反的沿锚索轴向的预应力，模拟真实的锚索预张拉的全部过程，减小了 -3-

中国科技论文在线由于计算过程带来的预应力损失。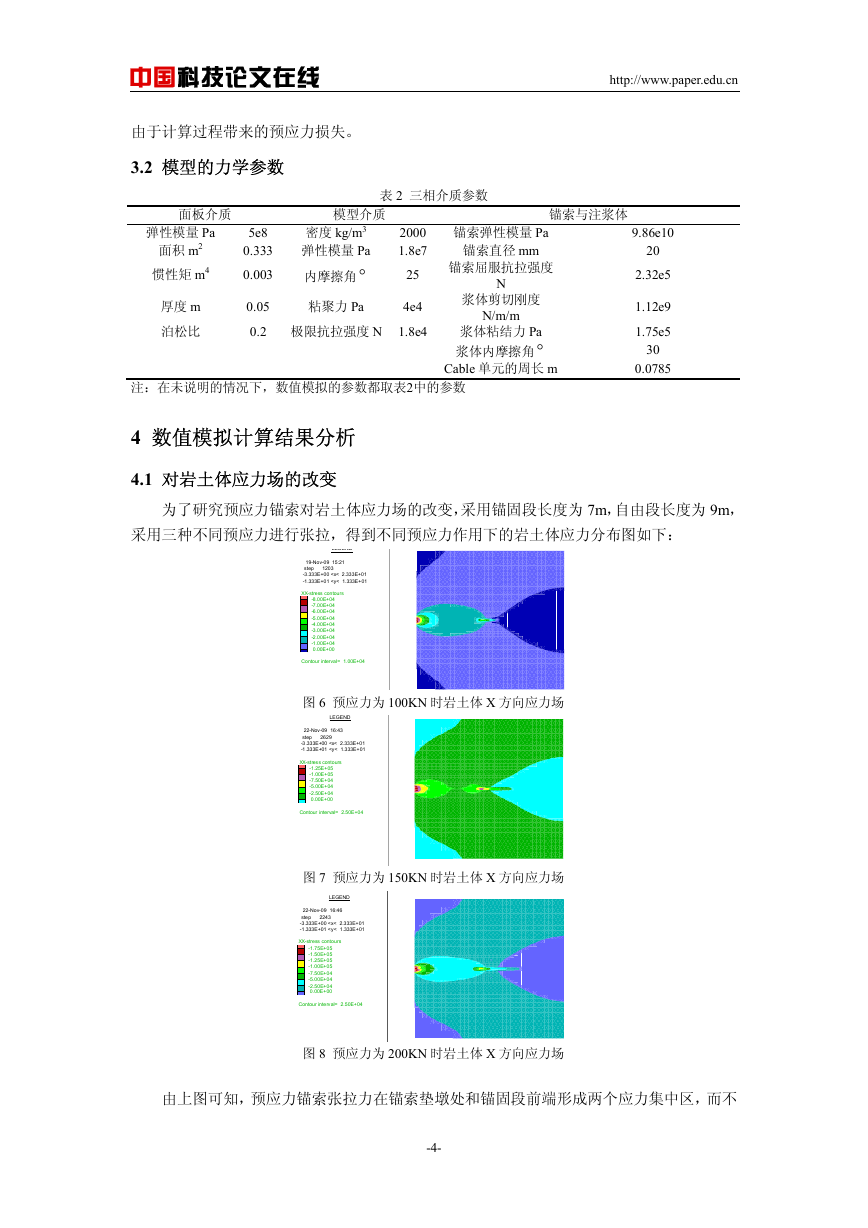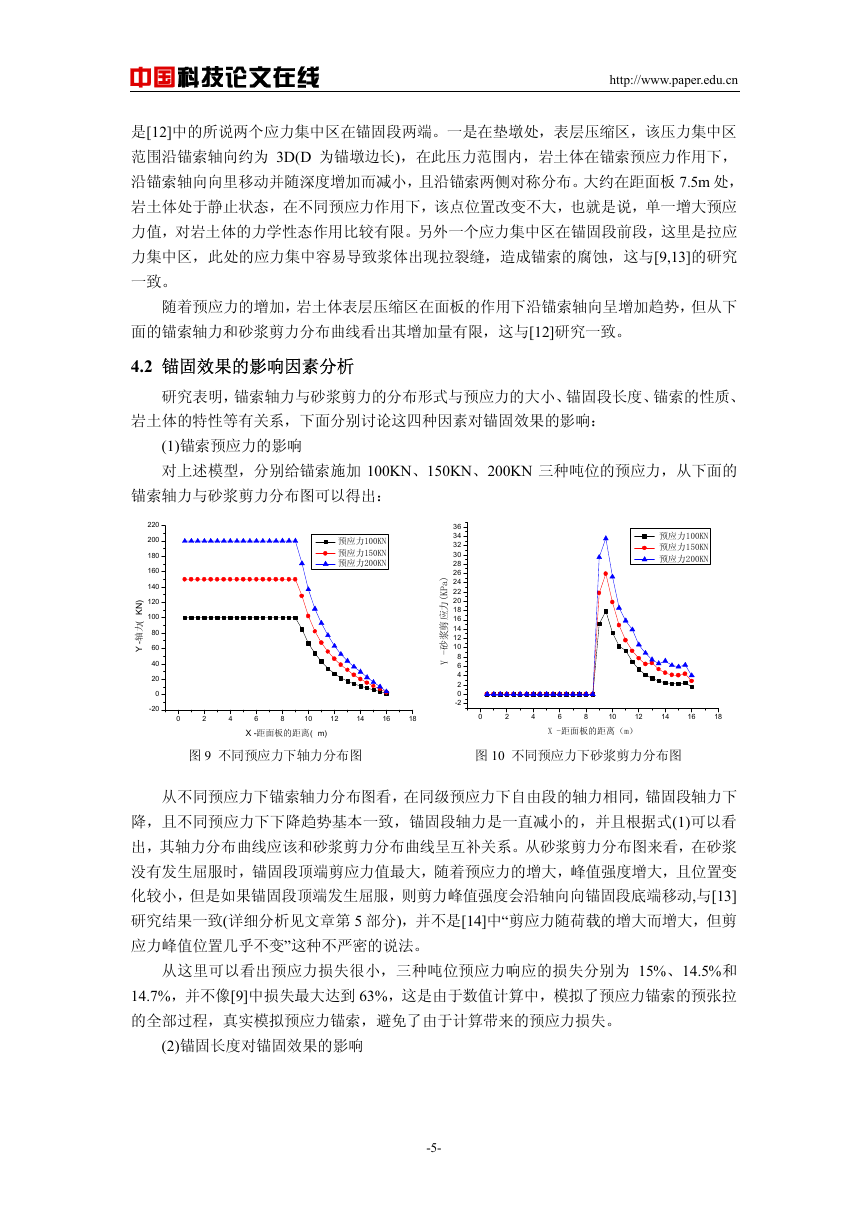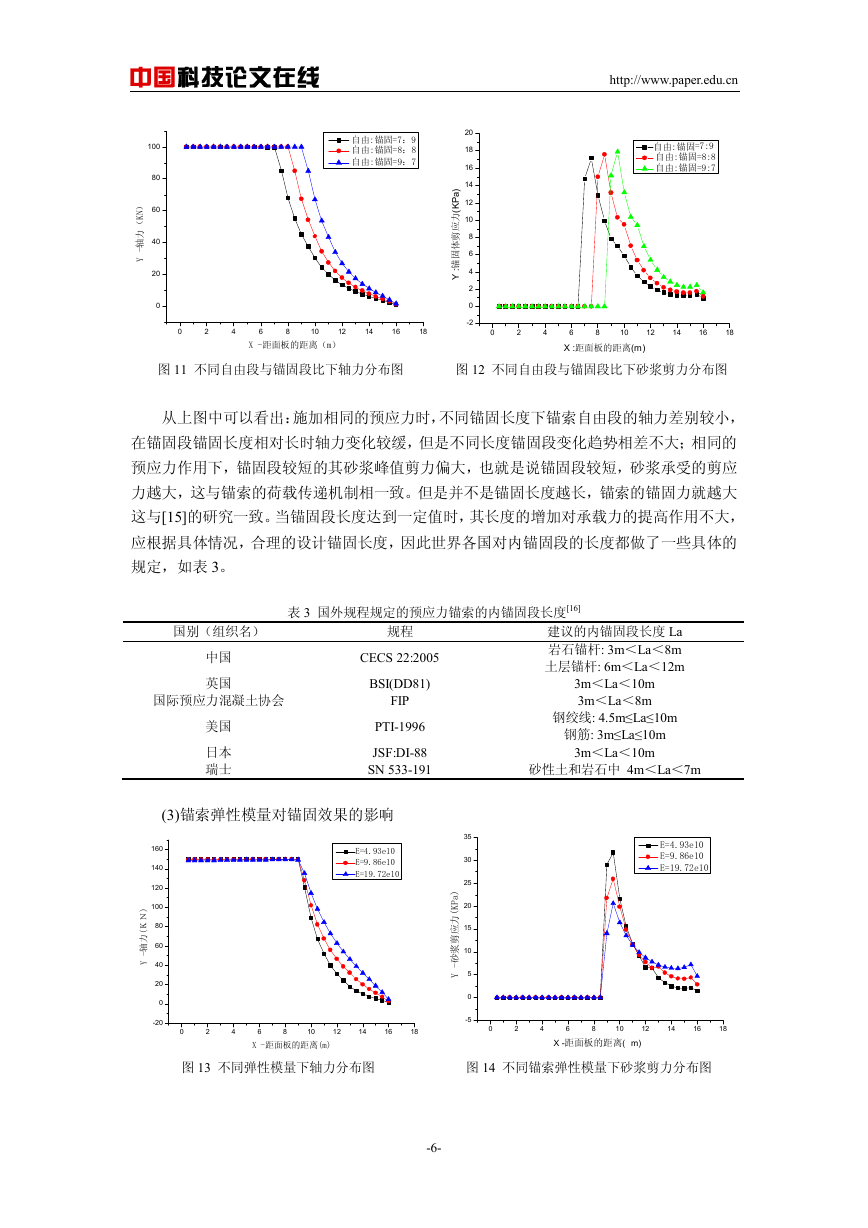 3.2 模型的力学参数表 2 三相介质参数 http://www.paper.edu.cn 锚索与注浆体 9.86e10 20 2.32e5 1.12e9 1.75e5 30 0.0785 面板介质弹性模量 Pa 面积 m2 惯性矩 m4 模型介质密度 kg/m3 5e8 0.333 弹性模量 Pa 内摩擦角° 0.003 锚索弹性模量 Pa 2000 1.8e7 25 锚索屈服抗拉强度锚索直径 mm N 厚度 m 泊松比粘聚力 Pa 0.05 4e4 0.2 极限抗拉强度 N 1.8e4 浆体剪切刚度 N/m/m 浆体粘结力 Pa 浆体内摩擦角° Cable 单元的周长 m 注：在未说明的情况下，数值模拟的参数都取表2中的参数 4 数值模拟计算结果分析 4.1 对岩土体应力场的改变为了研究预应力锚索对岩土体应力场的改变，采用锚固段长度为 7m，自由段长度为 9m，采用三种不同预应力进行张拉，得到不同预应力作用下的岩土体应力分布图如下： LEGEND 19-Nov-09 15:21 step 1203 -3.333E+00

中国科技论文在线 http://www.paper.edu.cn 是[12]中的所说两个应力集中区在锚固段两端。一是在垫墩处，表层压缩区，该压力集中区范围沿锚索轴向约为 3D(D 为锚墩边长)，在此压力范围内，岩土体在锚索预应力作用下，沿锚索轴向向里移动并随深度增加而减小，且沿锚索两侧对称分布。大约在距面板 7.5m 处，岩土体处于静止状态，在不同预应力作用下，该点位置改变不大，也就是说，单一增大预应力值，对岩土体的力学性态作用比较有限。另外一个应力集中区在锚固段前段，这里是拉应力集中区，此处的应力集中容易导致浆体出现拉裂缝，造成锚索的腐蚀，这与[9,13]的研究一致。随着预应力的增加，岩土体表层压缩区在面板的作用下沿锚索轴向呈增加趋势，但从下面的锚索轴力和砂浆剪力分布曲线看出其增加量有限，这与[12]研究一致。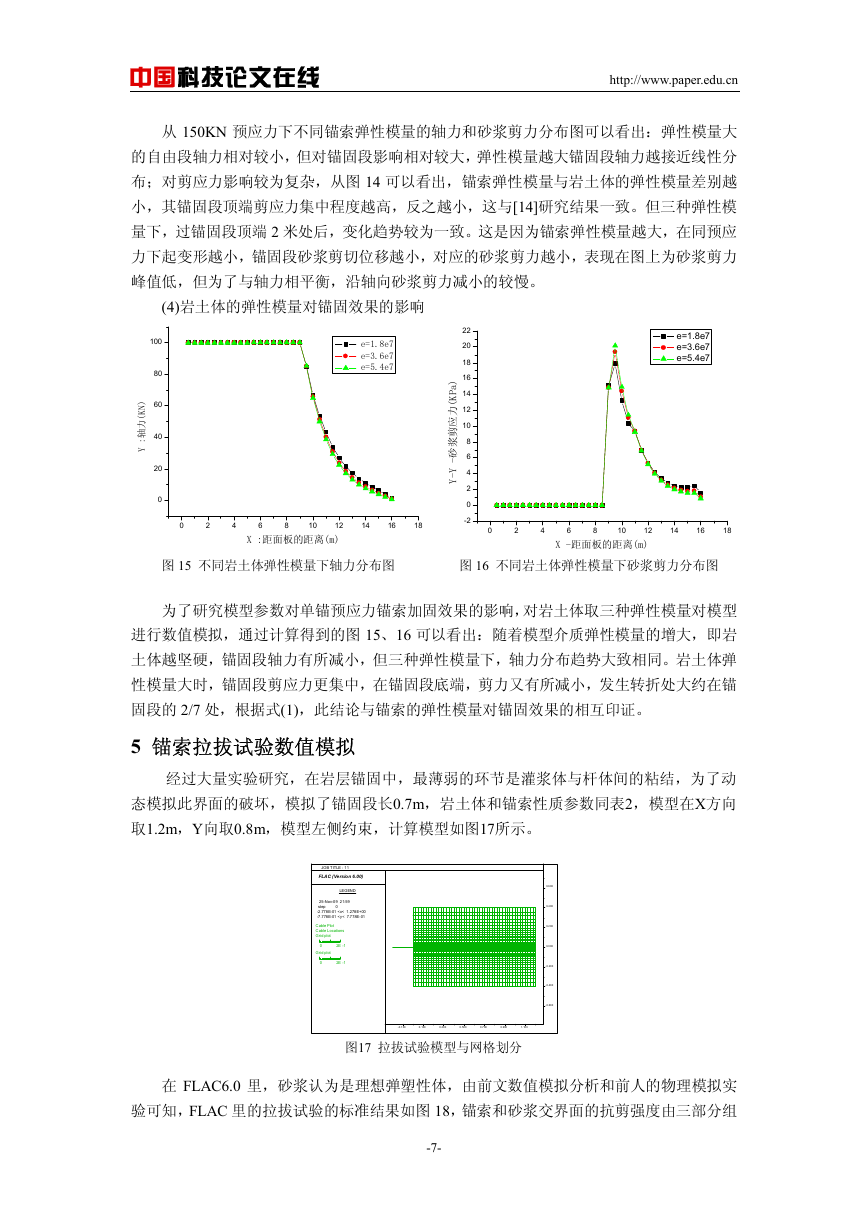 4.2 锚固效果的影响因素分析研究表明，锚索轴力与砂浆剪力的分布形式与预应力的大小、锚固段长度、锚索的性质、岩土体的特性等有关系，下面分别讨论这四种因素对锚固效果的影响： (1)锚索预应力的影响对上述模型，分别给锚索施加 100KN、150KN、200KN 三种吨位的预应力，从下面的锚索轴力与砂浆剪力分布图可以得出： 220 200 180 160 140 120 100 80 60 40 20 0 -20 ) N K ( 力轴 - Y 预应力100KN 预应力150KN 预应力200KN 预应力100KN 预应力150KN 预应力200KN 36 34 32 30 28 26 24 22 20 18 16 14 12 10 8 6 4 2 0 -2 ) a P K ( 力应剪浆砂 - Y 0 2 4 6 8 10 12 14 16 18 0 2 4 6 8 10 12 14 16 18 X -距面板的距离( m) X -距面板的距离（m）图 9 不同预应力下轴力分布图图 10 不同预应力下砂浆剪力分布图从不同预应力下锚索轴力分布图看，在同级预应力下自由段的轴力相同，锚固段轴力下降，且不同预应力下下降趋势基本一致，锚固段轴力是一直减小的，并且根据式(1)可以看出，其轴力分布曲线应该和砂浆剪力分布曲线呈互补关系。从砂浆剪力分布图来看，在砂浆没有发生屈服时，锚固段顶端剪应力值最大，随着预应力的增大，峰值强度增大，且位置变化较小，但是如果锚固段顶端发生屈服，则剪力峰值强度会沿轴向向锚固段底端移动,与[13] 研究结果一致(详细分析见文章第 5 部分)，并不是[14]中“剪应力随荷载的增大而增大，但剪应力峰值位置几乎不变”这种不严密的说法。从这里可以看出预应力损失很小，三种吨位预应力响应的损失分别为 15%、14.5%和 14.7%，并不像[9]中损失最大达到 63%，这是由于数值计算中，模拟了预应力锚索的预张拉的全部过程，真实模拟预应力锚索，避免了由于计算带来的预应力损失。 (2)锚固长度对锚固效果的影响 -5-

中国科技论文在线 http://www.paper.edu.cn ） N K （力轴 - Y 100 80 60 40 20 0 自由:锚固=7：9 自由:锚固=8：8 自由:锚固=9：7 ( ) a P K 力应剪体固锚 : Y 0 2 4 6 8 10 12 14 16 18 X -距面板的距离（m） 20 18 16 14 12 10 8 6 4 2 0 -2 0 2 4 自由:锚固=7:9 自由:锚固=8:8 自由:锚固=9:7 12 14 16 18 8 6 X :距面板的距离(m) 10 图 11 不同自由段与锚固段比下轴力分布图从上图中可以看出：施加相同的预应力时，不同锚固长度下锚索自由段的轴力差别较小，图 12 不同自由段与锚固段比下砂浆剪力分布图在锚固段锚固长度相对长时轴力变化较缓，但是不同长度锚固段变化趋势相差不大；相同的预应力作用下，锚固段较短的其砂浆峰值剪力偏大，也就是说锚固段较短，砂浆承受的剪应力越大，这与锚索的荷载传递机制相一致。但是并不是锚固长度越长，锚索的锚固力就越大这与[15]的研究一致。当锚固段长度达到一定值时，其长度的增加对承载力的提高作用不大，应根据具体情况，合理的设计锚固长度，因此世界各国对内锚固段的长度都做了一些具体的规定，如表 3。表 3 国外规程规定的预应力锚索的内锚固段长度[16] 国别（组织名）中国英国国际预应力混凝土协会规程 CECS 22:2005 BSI(DD81) FIP 美国日本瑞士 PTI-1996 JSF:DI-88 SN 533-191 (3)锚索弹性模量对锚固效果的影响建议的内锚固段长度 La 岩石锚杆: 3m＜La＜8m 土层锚杆: 6m＜La＜12m 3m＜La＜10m 3m＜La＜8m 钢绞线: 4.5m≤La≤10m 钢筋: 3m≤La≤10m 3m＜La＜10m 砂性土和岩石中 4m＜La＜7m ) ＮＫ ( 力轴 - Y 160 140 120 100 80 60 40 20 0 -20 E=4.93e10 E=9.86e10 E=19.72e10 E=4.93e10 E=9.86e10 E=19.72e10 35 30 25 20 15 10 5 0 -5 ) a P K ( 力应剪浆砂 - Y 0 2 4 6 8 10 12 14 16 18 0 2 4 6 8 10 12 14 16 18 X -距面板的距离(m) X -距面板的距离( m) 图 13 不同弹性模量下轴力分布图图 14 不同锚索弹性模量下砂浆剪力分布图 -6-

中国科技论文在线 http://www.paper.edu.cn 从 150KN 预应力下不同锚索弹性模量的轴力和砂浆剪力分布图可以看出：弹性模量大的自由段轴力相对较小，但对锚固段影响相对较大，弹性模量越大锚固段轴力越接近线性分布；对剪应力影响较为复杂，从图 14 可以看出，锚索弹性模量与岩土体的弹性模量差别越小，其锚固段顶端剪应力集中程度越高，反之越小，这与[14]研究结果一致。但三种弹性模量下，过锚固段顶端 2 米处后，变化趋势较为一致。这是因为锚索弹性模量越大，在同预应力下起变形越小，锚固段砂浆剪切位移越小，对应的砂浆剪力越小，表现在图上为砂浆剪力峰值低，但为了与轴力相平衡，沿轴向砂浆剪力减小的较慢。 (4)岩土体的弹性模量对锚固效果的影响 100 80 60 40 20 0 ) N K ( 力轴 : Y 0 2 4 e=1.8e7 e=3.6e7 e=5.4e7 14 16 18 8 6 12 X :距面板的距离(m) 10 ) a P K ( 力应剪浆砂 - Y - Y 22 20 18 16 14 12 10 8 6 4 2 0 -2 0 2 4 8 6 12 X -距面板的距离(m) 10 e=1.8e7 e=3.6e7 e=5.4e7 14 16 18 图 15 不同岩土体弹性模量下轴力分布图为了研究模型参数对单锚预应力锚索加固效果的影响，对岩土体取三种弹性模量对模型进行数值模拟，通过计算得到的图 15、16 可以看出：随着模型介质弹性模量的增大，即岩土体越坚硬，锚固段轴力有所减小，但三种弹性模量下，轴力分布趋势大致相同。岩土体弹图 16 不同岩土体弹性模量下砂浆剪力分布图性模量大时，锚固段剪应力更集中，在锚固段底端，剪力又有所减小，发生转折处大约在锚固段的 2/7 处，根据式(1)，此结论与锚索的弹性模量对锚固效果的相互印证。 5 锚索拉拔试验数值模拟经过大量实验研究，在岩层锚固中，最薄弱的环节是灌浆体与杆体间的粘结，为了动态模拟此界面的破坏，模拟了锚固段长0.7m，岩土体和锚索性质参数同表2，模型在X方向取1.2m，Y向取0.8m，模型左侧约束，计算模型如图17所示。 JOB TITLE : 11 FLAC (Version 6.00) LEGEND 25-Nov-09 21:59 step 0 -2.778E-01

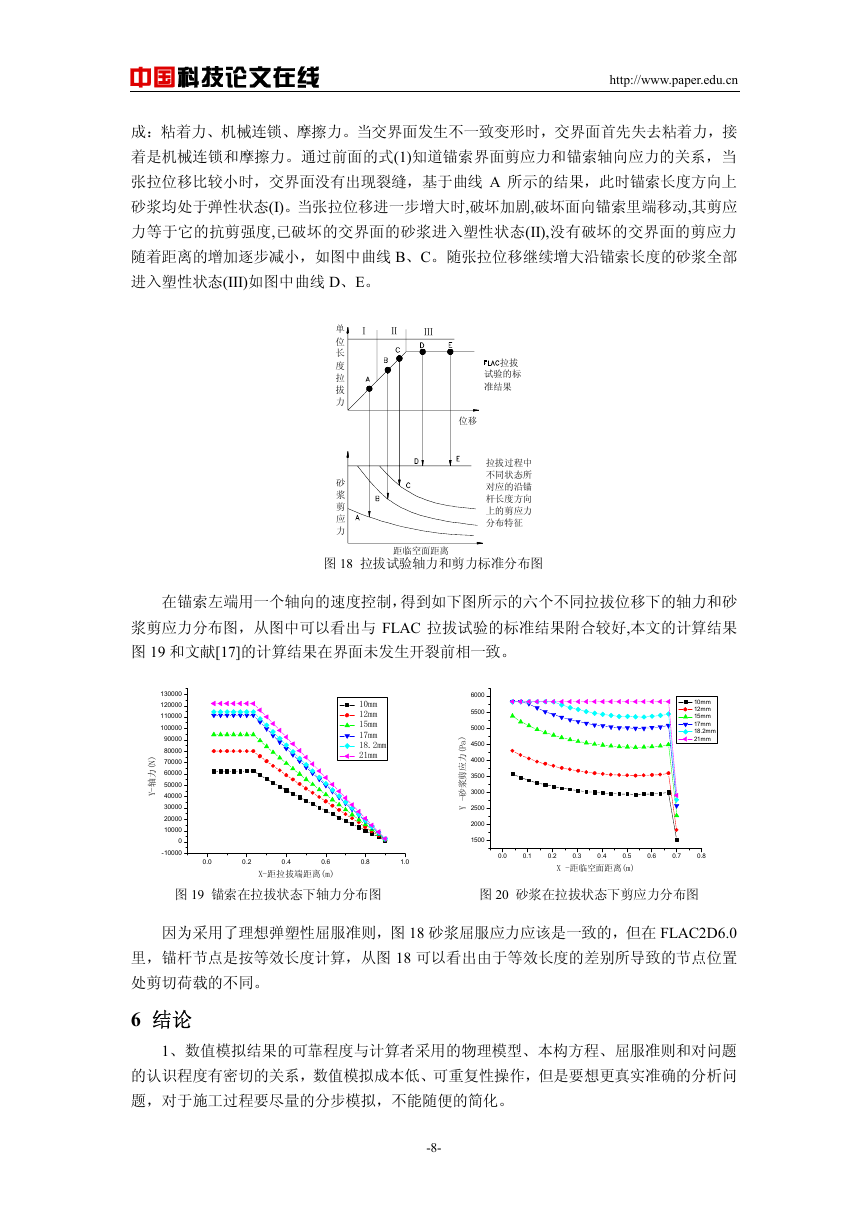
中国科技论文在线 http://www.paper.edu.cn 成：粘着力、机械连锁、摩擦力。当交界面发生不一致变形时，交界面首先失去粘着力，接着是机械连锁和摩擦力。通过前面的式(1)知道锚索界面剪应力和锚索轴向应力的关系，当张拉位移比较小时，交界面没有出现裂缝，基于曲线 A 所示的结果，此时锚索长度方向上砂浆均处于弹性状态(I)。当张拉位移进一步增大时,破坏加剧,破坏面向锚索里端移动,其剪应力等于它的抗剪强度,已破坏的交界面的砂浆进入塑性状态(II),没有破坏的交界面的剪应力随着距离的增加逐步减小，如图中曲线 B、C。随张拉位移继续增大沿锚索长度的砂浆全部进入塑性状态(III)如图中曲线 D、E。 Ⅰ Ⅱ Ⅲ 单位长度拉拔力砂浆剪应力拉拔试验的标准结果位移拉拔过程中不同状态所对应的沿锚杆长度方向上的剪应力分布特征图 18 拉拔试验轴力和剪力标准分布图距临空面距离在锚索左端用一个轴向的速度控制，得到如下图所示的六个不同拉拔位移下的轴力和砂浆剪应力分布图，从图中可以看出与 FLAC 拉拔试验的标准结果附合较好,本文的计算结果图 19 和文献[17]的计算结果在界面未发生开裂前相一致。 130000 120000 110000 100000 90000 80000 70000 60000 50000 40000 30000 20000 10000 0 -10000 ) N ( 力轴 - Y 10mm 12mm 15mm 17mm 18.2mm 21mm 0.0 0.2 0.4 0.6 X-距拉拔端距离(m) 0.8 1.0 图 19 锚索在拉拔状态下轴力分布图 6000 5500 5000 4500 4000 3500 3000 2500 2000 1500 ) a P ( 力应剪浆砂 - Y 0.0 0.1 10mm 12mm 15mm 17mm 18.2mm 21mm 0.6 0.7 0.8 0.2 0.3 0.5 X -距临空面距离(m) 0.4 图 20 砂浆在拉拔状态下剪应力分布图因为采用了理想弹塑性屈服准则，图 18 砂浆屈服应力应该是一致的，但在 FLAC2D6.0 里，锚杆节点是按等效长度计算，从图 18 可以看出由于等效长度的差别所导致的节点位置处剪切荷载的不同。 6 结论 1、数值模拟结果的可靠程度与计算者采用的物理模型、本构方程、屈服准则和对问题的认识程度有密切的关系，数值模拟成本低、可重复性操作，但是要想更真实准确的分析问题，对于施工过程要尽量的分步模拟，不能随便的简化。 -8-

分享到：

赞收藏

资料库

预应力锚索的锚固机理与锚固效应影响因素的数值仿真试验 .pdf

相关推荐

开发技术

热门标签

最新资料