logo资料库

2017年全国大学生数学建模竞赛论文(推荐国二)原版-供学习.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：1.20M 资料格式：docx 举报 版权申诉
第1页 / 共37页
第2页 / 共37页
第3页 / 共37页
第4页 / 共37页
第5页 / 共37页
第6页 / 共37页
第7页 / 共37页
第8页 / 共37页
资料共37页，剩余部分请下载后查看
    1引言
    1.1问题背景
    1.2问题重述
    2问题分析
    2.1问题一分析
    2.2问题二和问题三分析
    2.3问题四分析
    3模型假设
    4名词解释与符号说明
    4.1名词解释
    4.2符号说明
    5模型建立与求解
    5.1问题一的模型建立与求解
    5.1.1坐标系建立和CT系统旋转分析
    5.1.2附件数据处理和分析
    5.1.3问题一模型建立
    5.1.4问题一模型求解
    5.2问题二和问题三的模型建立与求解
    5.2.1滤波反投影法成像模型
    5.2.2卷积反投影法成像模型
    5.2.3未知介质的位置确定模型
    5.2.4问题二模型求解
    5.2.5问题三模型求解
    5.3问题四的模型建立与求解
    5.3.1新的标定模型
    6模型的检验
    6.1误差分析和改善
    7模型的评价与推广
    7.1模型的评价
    7.1.1模型优点
    7.1.2模型缺点
    7.2模型的推广
    8参考文献
    基于变换、滤波和反投影的 CT 系统参数标定及成像方法研究 摘要 由于二维 CT 系统在安装时存在误差，从而影响成像质量，因此，建立模型对安装 好的 CT 系统进行参数标定，以及利用 CT 系统获得的接收信息进行图像重建具有重要 意义。本文利用 matlab 软件对二维 CT 系统的参数标定进行研究，提出 CT 系统旋转中 心的确定方法、探测器单元之间的距离的确立模型、CT 系统使用的 X 射线的 180 个方 向的确立模型。同时，提供基于 CT 系统接收信息和标定参数的未知介质位置、几何形 状、吸收率等信息的确定方案，并给出优化后的标定模板。 D  针对问题一，从附件 1 中获取前 10 组数据，提取出固体介质圆柱的对应接收信息， 进而计算每组接收信息对应的有效探测器个数，结合圆的直径，计算探测器单元之间的 。，以正方形托盘中心为原点建立平面直角坐标系，比较 CT 系统旋 距离 0.2768mm 转中心处于正方形托盘中心的位置和处于实际安装位置时接收信息的差别，利用坐标变 换公式，求出 CT 系统旋转中心的位置坐标为(-9.2734,5.5363)(单位：mm)。分析椭圆在 探测器平面上的投影长度和接收信息组号的关系以及椭圆投影长度和 X 射线方向的关 系，联立求解得 X 射线方向和椭圆投影长度的函数关系，从而求得 X 射线的 180 个方 向。 针对问题二和问题三，本文提出一种基于滤波和反投影的 CT 系统成像方法。对每 个角度下的投影数据，求取一维傅里叶变换，然后滤波，接着求取滤波后的数据的一维 傅里叶逆变换，最后反投影，得到重建后的图像。和先卷积后反投影方法比较，发现该 基于滤波和反投影的 CT 系统成像方法更容易实现、更快捷。利用基于滤波和反投影的 CT 系统成像方法，可以得到未知介质的形状。结合问题一求解到的 CT 旋转中心的位 置坐标可以计算得到未知介质在正方形托盘中的位置，从而确定吸收率分布。 针对问题四，本文提出一种双圆组合标定模板，两个半径均为 4mm 的圆，圆心分 别位于正方形托盘中心以及(45,0)处，利用两个圆的圆心位置变化确定探测器单元之间 的距离、CT 系统旋转中心的位置坐标和 X 射线的 180 个方向，从而减少在问题一当中 处理数据所带来的误差并且把长度计算转化为一个点的位置计算，根据附件的数据特 点，减少了 X 射线方向相同的可能性，提高了模型的精度和准确度，对 CT 系统参数标 定具有重要意义。 关键词：CT 系统 参数标定 图像重建 傅里叶变换 滤波反投影(FBP) 1
    1 引言 1.1 问题背景 CT(Computed Tomography)是现代电子计算机控制技术和 X 射线摄影技术相结合的 产物，在医学诊断和工业无损检测上具有重要地位。CT 可以在不破坏样品的情况下， 依据辐射在被检测物体中的减弱和吸收特性以及探测器的扫描结果，对生物组织和工程 材料的样品进行断层成像，由此获取样品内部的结构信息。 现有一种典型的二维 CT 系统如图 1 所示，平行入射的 X 射线垂直于探测器平面， 每个等距的探测器单元（共 512 个）可看成一个接收点。X 射线的发射器和探测器相对 位置固定不变，而后整个发射--接收系统绕某固定的旋转中心逆时针旋转 180 次。对每 一个 X 射线方向，在探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线 能量，经过增益等处理后就能得到 180 组与未知介质相关的接收信息。 然而 CT 系统安装时往往存在误差，从而影响成像质量，因此需要对安装好的 CT 系统进行参数标定，即借助于已知结构的样品（称为模板）标定 CT 系统的参数，从而 并据此对未知结构的样品进行成像。 图 1 CT 系统示意图 1.2 问题重述 (1) 在正方形托盘上放置两个均匀固体介质组成的标定模板，模板的几何信息如图 2 所 示，相应的数据文件见附件 1，其中每一点的数值反映了该点的吸收强度，这里称 为“吸收率”。对应于该模板的接收信息见附件 2。请根据这一模板及其接收信息， 2
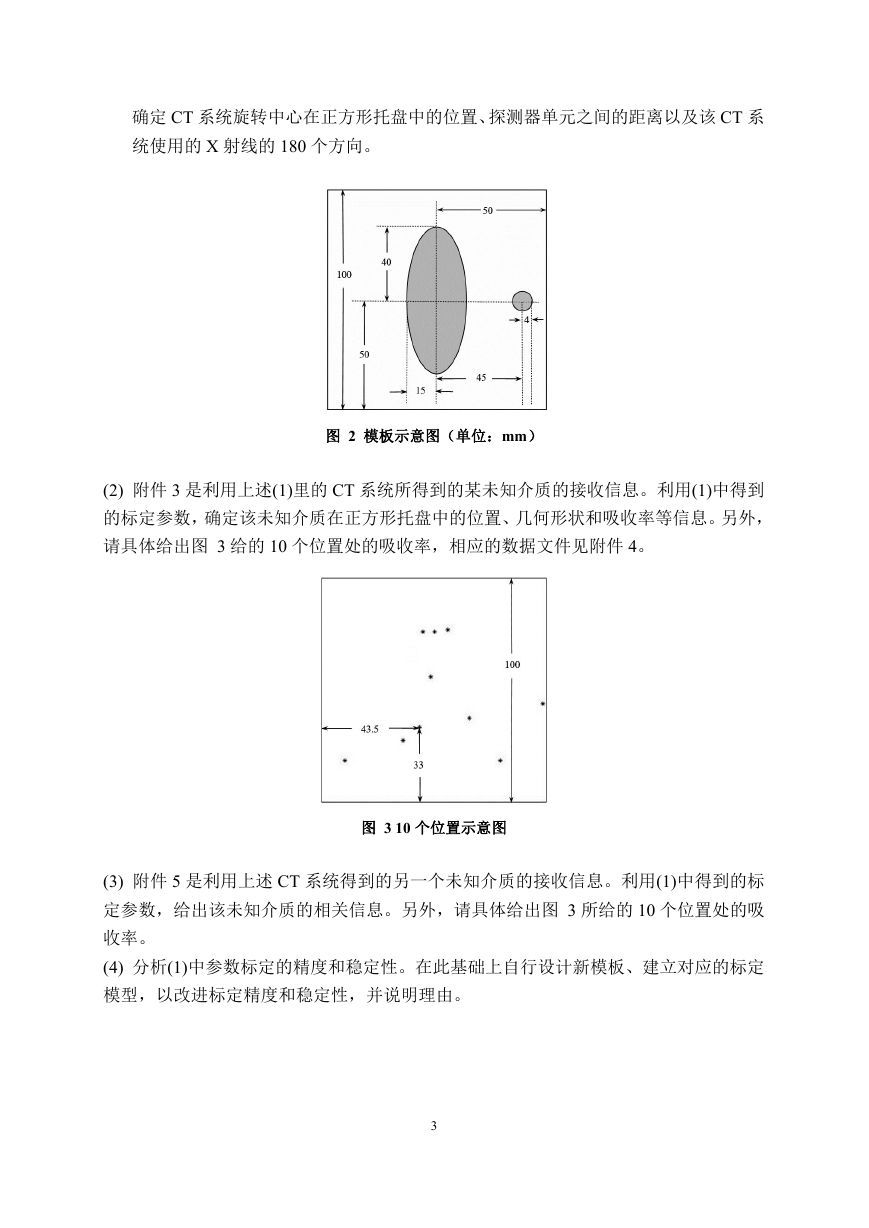
    确定 CT 系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该 CT 系 统使用的 X 射线的 180 个方向。 图 2 模板示意图（单位：mm） (2) 附件 3 是利用上述(1)里的 CT 系统所得到的某未知介质的接收信息。利用(1)中得到 的标定参数，确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息。另外， 请具体给出图 3 给的 10 个位置处的吸收率，相应的数据文件见附件 4。 图 3 10 个位置示意图 (3) 附件 5 是利用上述 CT 系统得到的另一个未知介质的接收信息。利用(1)中得到的标 定参数，给出该未知介质的相关信息。另外，请具体给出图 3 所给的 10 个位置处的吸 收率。 (4) 分析(1)中参数标定的精度和稳定性。在此基础上自行设计新模板、建立对应的标定 模型，以改进标定精度和稳定性，并说明理由。 3
    2 问题分析 2.1 问题一分析 问题一要求我们利用附件 1 和附件 2 的数据，确定 CT 系统旋转中心在正方形托盘 中的位置、探测器单元之间的距离以及该 CT 系统使用 X 射线的 180 个方向。利用 matlab 将附件 1 和附件 2 的数据可视化，然后根据图 2，结合附件 2，选取 10 组标定模板的接 收信息，获取均匀固体介质球(半径 4mm)对应的探测器单元数目，进而计算探测器单元 之间的距离。通过比较旋转中心和正方形托盘中心重合时，CT 系统被椭圆长轴所在直 线穿过的探测器编号、被椭圆短轴所在直线穿过的探测器编号和旋转中心处于实际位置 时，CT 系统被椭圆长轴所在直线穿过的探测器编号、被椭圆短轴所在直线穿过的探测 器编号，结合探测器单元之间的距离可以求出 CT 系统旋转中心在正方形托盘中的位置。 最后，利用两平行且与椭圆相切的动直线之间的距离和直线的倾斜角的关系，结合 180 组接收信息，可以计算出该 CT 系统使用的 X 射线的 180 个方向，利用一阶数据拟合可 对其进一步优化，以方便问题二和问题三的求解。 2.2 问题二和问题三分析 问题二要求我们利用问题一求解的 CT 系统旋转中心在正方形托盘中的位置、探测 器单元之间的距离以及该 CT 系统使用的 X 射线的 180 个方向，结合附件的数据给出的 接收信息，确定未知介质的位置、几何形状和吸收率。本文分别采用先滤波后反投影以 及先卷积后反投影两种方法实现图像重建。比较两者的难易程度和成像质量，从而选择 出更适合的图像重建模型。比较不滤波、Ram-Lak 滤波、Ram-Lak Cosine 滤波、Ram-Lak Hamming 滤波这几种情形的图像重建效果，进一步优化整个成像过程。利用 matlab 编 程求解。 2.3 问题四分析 问题四要求我们分析问题一中参数标定的精度和稳定性。在问题一的求解过程当中，影 响精度和稳定性的主要因素为有效接收探测器数目的波动性、最值的非唯一性以及角度 计算时投影长度的不准确性。而且这三个因素互相影响，其中一个的误差会致使其他两 个因素造成的误差累积放大。因此我们考虑用圆代替椭圆，用圆心轨迹变化代替投影长 度变化，从而提高该 CT 系统标定的精度和稳定性。 4
    3 模型假设  假设 1：假设均匀固体介质的每一点的吸收率只有 0 和 1 两种可能。  假设 2：假设沿任意角度，X 射线始终覆盖整个正方形托盘，不存在没有 X 射线经 过的区域。  假设 3：假设托盘以及在托盘上的介质没有自觉或不自觉的运动，探测器之间响应 一致且没有射束硬化以及采样频率合适，从而不会产生伪影。  假设 4：假设附件提供的数据能客观反映实际情况，没有错误数据，不考虑数据的 测量误差。  假设 5：假设整个发射接收系统在 180 次旋转过程中，不存在停留现象，也就是不 存在两组接收信息在同一个 X 射线方向下测量得到。  假设 6：确定 CT 系统的旋转中心和 X 射线的 180 个方向后，在以后的每一次测量 当中，CT 系统的旋转中心以及 X 射线的 180 个方向和标定的参数一致，也就是附 件 2、附件 3 和附件 5 是在完全相同的条件下得到的。 4 名词解释与符号说明 4.1 名词解释 1) 吸收率：均匀固体介质每一点对 X 射线吸收的强度。 2) 有效探测器：探测器检测到 X 射线，并且反映在接收信息当中为非 0 值，也就是对 应的接收信息为非 0 值的探测器。 3) 椭圆/圆的有效探测器：指接收到的信息是 X 射线穿过椭圆/圆部分固体介质得到的 探测器。 4) 椭圆/圆的投影长度：指在某次探测当中，椭圆/圆的有效探测器与探测器单元之间 的距离的乘积。 5) 滤波：将图像信号当中特定波段频率滤除，以使图像更加清晰。 6) 反投影[1]：反投影的基本思想是断层内该点的密度值就是经过该平面上的一点的 X 射线投影之和。 7) 中心切片定理[2]：二维函数图像  , f x y 在视角为时的投影   r P x 的一维傅里叶变 换,  , f x y 的二维傅里叶变换  F    2 , 1    F    , 与探测器平行的方向，而且过原点 的的一个切片。是切片与 1轴所成的夹角。 5
    4.2 符号说明 表 1 符号说明 符号 说明 Ab 1Ab 3Ab 5Ab Re Re 2 Re3 Re5 x y id g Xc Yc D g Co gL ,g cL ,g eL g 吸收率（Absorptivity）/吸收强度 附件 1 对应的吸收率（Absorptivity）/吸收强度 附件 3 对应的吸收率（Absorptivity）/吸收强度 附件 5 对应的吸收率（Absorptivity）/吸收强度 接收信息（Receive information） 附件 2 的接收信息（Receive information） 附件 3 的接收信息（Receive information） 附件 5 的接收信息（Receive information） 正方形托盘横坐标 正方形托盘纵坐标 探测器的标号 i detector 接收信息组号（group） CT 系统旋转中心横坐标 CT 系统旋转中心纵坐标 探测器单元之间的距离 D（Distance） 第 g 组接收信息对应的 X 射线和 x 轴正方向的夹角 附件 4 给定的位置（Coordinate） 第 g 组接收信息指定介质的投影长度 第 g 组接收信息对应标定模板中圆的投影长度 第 g 组接收信息对应标定模板中椭圆的投影长度 第 g 组接收信息对应的探测器平面 x 轴正方向的夹角 6
    5 模型建立与求解 5.1 问题一的模型建立与求解 对于问题一，我们采用算术平均值和坐标变换公式求解探测器单元之间的距离、CT 系统旋转中心坐标，然后建立椭圆投影长度和表示 X 射线方向的 g 之间的函数关系，进 而通过求解 180 组椭圆投影长度获得 X 射线的 180 个方向。 5.1.1 坐标系建立和 CT 系统旋转分析 为了方便问题的求解，我们以正方形托盘的中心为原点，水平向右为 x 轴正方向， 建立平面直角坐标系，如图 4(a)图所示。 图 4 坐标建立和旋转分析示意图 整个 CT 系统在旋转过程中，可以分为三种情况：X 射线穿过椭圆、圆后在探测器 平面上的投影不重合、X 射线穿过椭圆、圆后在探测器平面上的投影重合、X 射线与椭 圆、圆的内公切线平行(临界条件)，见图 4 中的(b)、(c)、(d)。 7
    这样，根据起始的投影情况以及旋转方向(逆时针)就可以确定初始的 X 射线方向。 5.1.2 附件数据处理和分析 附件 1 给出了标定模板的吸收率，附件 2 给出了对应标定模板的 180 组接收信息， 为了方便问题一的分析和求解。我们利用 matlab 对附件 1 和附件 2 进行了数据的可视化 处理。 对附件 1，可以用 matlab 得到图 5 所示的标定模板吸收率分布图。从图中可以看到， 吸收率只有 0 和 1 两种状态。 (a) 吸收率分布图(立体) (b) 沿 x 轴正方向和 y 轴正方向观测 图 5 标定模板吸收率分布图 对附件 2，我们分别进行接收信息的三维可视化和二维可视化，得到图 6 所示的分 布图。从图 6(a)可以知道，接收信息最大值点只有一个，对应于 X 射线沿 y 轴的情形； 从图 6(b)可以看到投影长度只存在一个最大值和一个最小值，利用该点信息可以唯一确 定 CT 系统的旋转中心，且前 10 组接收信息当中，圆和椭圆没有重合，因此可以利用前 10 组接收信息求解探测器单元之间的宽度。 (a) 接收信息分布图(立体) (b) 接收信息分布图(平面) 图 6 标定模板接收信息与组号、探测器的关系图 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料