第1页 / 共18页
第2页 / 共18页
第3页 / 共18页
第4页 / 共18页
第5页 / 共18页
第6页 / 共18页
第7页 / 共18页
第8页 / 共18页
最速下降法的改进和程序演示.docx
一、引言
二、最速下降法的基本原理
（一）无约束问题的最优性条件
（二）最速下降法的基本思想和迭代步骤
（三）负梯度方向使目标函数值下降最快的原因
（四）最速下降法的收敛性以及收敛速度
三、最速下降法程序流程图
四、例题
五、最速下降法的不足
（一）最速下降法中锯齿现象的成因分析：
（二）最速下降法的改进措施
六、结论与分析
七、总结与体会
八、参考文献
目录
一、引言
二、最速下降法的基本原理.....................................................................................................3
（一）无约束问题的最优性条件.......................................................................................3
（二）最速下降法的基本思想和迭代步骤.................................................................... 4
（三）负梯度方向使目标函数值下降最快的原因...................................................... 4
（四）最速下降法的收敛性以及收敛速度.................................................................... 5
三、最速下降法程序流程图.....................................................................................................6
四、例题..........................................................................................................................................6
五、最速下降法的不足........................................................................................................... 10
（一）最速下降法中锯齿现象的成因分析：............................................................. 10
（二）最速下降法的改进措施.........................................................................................11
六、结论与分析......................................................................................................................... 16
七、总结与体会......................................................................................................................... 17
八、参考文献..............................................................................................................................18
摘要
最速下降法又称为梯度法，是求解无约束优化问题的一种基本而重要的方法。其优点在
于程序简单、计算量小，并且对初始点没有特别的要求，因此广泛应用于军事、经济、管理
等方面。缺点则在于收敛慢，效率不高，有时达不到最优解，容易产生“锯齿现象”。于是
研究和优化最速下降法及其算法实现有着及其重要的意义。本文主要介绍了最速下降法的基
本原理、“锯齿现象”的成因分析和改善措施，以及 BB 最速下降法的原理介绍。目的是了解
最速下降法的核心内容，分析其优缺点并给出改善措施。
关键词：最速下降法，锯齿现象，BB 最速下降法
Abstract
The steepest descent method, also called gradient method, is a basic and important method
for solving unconstrained optimization problems. Its advantages are simple procedures, small
amount of calculation, and no special requirements for the initial point, so it is widely used in
military, economic, management and other aspects. The disadvantage is that the convergence is
slow, the efficiency is not high, sometimes the optimal solution is not achieved, and the “sawtooth
phenomenon” is easily generated. Therefore, it is of great significance to study and optimize the
steepest descent method and its algorithm implementation. This article mainly introduces the basic
principle of the steepest descent method, the causes of the "sawtooth phenomenon" analysis and
improvement measures, and the introduction of the principle of the BB （ Barzilar, Borwein ）
descent method. The purpose is to understand the core content of the steepest descent method,
analyze its advantages and disadvantages, and give improvement measures.
Key words：Steepest descent method，Sawtooth phenomenon，BB（Barzilar, Borwein）
descent method
一、引言
最速下降法又称为梯度法，是 1847 年由著名数学家 Cauchy 给出的，它是解析法中最古
老的一种，其他解析方法或事它的变形，或是受它的启发而得到的，因此它是最优化方法的
基础。作为一种基础的算法，它在最优化方法中占有重要地位。非线性规划研究的对象是非
线性函数的数值优化问题，它的理论和方法渗透到许多方面，特别是军事、经济、管理、生
产过程自动化、工程设计和产品优化设计等方面有着重要的应用。而最速下降法正是 n 元函
数的无约束非线性问题 min ( )f x 的一种重要解析法，研究最速下降法原理及其算法实现有
着及其重要的意义。
在本次实验中，我们首先分析了最速下降法的基本原理和主要操作步骤，运用基于最速
下降法进行无约束问题的求解。最速下降法的核心是将 n 维问题转化为一系列沿负梯度方向
用一维搜索方法寻优的问题。但在实际应用过程中，由于收敛慢，容易产生“锯齿现象”，
由此我们进行了对“锯齿现象”的成因分析，利用 Matlab 软件，在 BB 最速下降法的原理
基础上，提出了对最速下降法的改进措施。
二、最速下降法的基本原理
（一）无约束问题的最优性条件
无约束问题的最优解所要满足的必要条件和充分条件是我们设计算法的依据，为此我
们有以下几个定理[1]：
定理 1 设
: n
f R
R 在点
1
x R
n
处可微，若存在
p R
n
则向量 p 是 f 在点 x 处的下降方向。
，使 ( )
Tf x p
，
0
定理 2 设
: n
f R
R 在点 x
1
nR
处可微，若x 是无约束问题的局部最优解，
x
则 f( )
。
0
x
由数学分析中我们已经知道，使 f( )
的点 x 为函数 f 的驻点或平稳点。函数 f
0
的一个驻点可以是极小点；也可以是极大点；甚至也可能既不是极小点也不是极大点，此时
称它为函数 f 的鞍点。以上定理告诉我们，x 是无约束问题的局部最优解的必要条件是：x
是其目标函数 f 的驻点。
: n
f R
R 在点 x
1
nR 处的 Hesse 矩阵 2 ( )f x
存在。若 2 ( )=0
f x
，
定理 3 设
并且 2 ( )f x
正定，则 x 是无约束问题的严格局部最优解。
一般而言，无约束问题的目标函数的驻点不一定是无约束问题的最优解。但对于其目标
函数是凸函数的无约束凸规划，下面定理证明了它的目标函数的驻点就是它的整体最优解。
定理 4 设
: n
f R
R ，x
1
x
nR ，f 是 nR 上的可微凸函数。若有 f( )
，
0
则x 是无约束问题的整体最优解。
（二）最速下降法的基本思想和迭代步骤
设无约束问题中的目标函数
: n
f R
R 一阶连续可微。
1
最速下降法的基本思想是：从当前点 kx 出发，取函数 f( )x 在点 kx 处下降最快的方
向最为搜索方向 pk 。由 f( )x 的 Taylor 展式知
k
f x
(
)
k
f x
(
k
p
)
k T k
)
f x p
(
k
(
p
)
k
略去 t 的告诫无穷小项不计，可见取 p
们可以构造出最速下降法的迭代步骤。
解无约束问题的最速下降法计算步骤
kf x
)
(
时，函数值下降得最多。于是，我
第 1 步 选取初始点 0x ，给定终止误差
0 ，令 k： 0 ；
第 2 步 计算 (
)kf x
，若 f(
)kx
，停止迭代，输出 kx ，否则进行第 3 步；
k
第 3 步 取 p
kf x
)
；
(
第 4 步 进 行 一 维 搜 索 ， 求 k ， 使 得
f(
k
x
k
p
k
)
k
f x
min (
0
k
p
)
， 令
k
1 x
k
x
k
p
k
，
k k
，转第 2 步。
1
由以上计算步骤可知，最速下降法迭代终止时，求得的是目标函数驻点的一个近似点。
确定最优步长 k 的方法如下：
方法一：采用任一种一维寻优法
此时的 f(
k
x
f x
(
k
))
已成为步长 的一元函数，故可用任何一种一维寻优法求
出 k ，即
f(
k
x
1
)
k
f x
(
k
k
f x
(
))
min (
k
f x
k
f x
(
))
（三）负梯度方向使目标函数值下降最快的原因
为什么是负梯度方向使目标函数值下降最快，我们讨论 n 维空间中的一个点移动到另一个点
之后，目标函数的改变情况，首先，直接写出代表最终目标函数值的数学表达式：
kf(
x
k
p f x
)
)
(
f x p
k
)
(
xk ：代表第 k 个点的自变量（一个向量）；
p ：单位方向（一个向量），即：
1p ；
：步长（一个实数）；
)kx
f(
： 的高阶无穷小
：目标函数在 xk 这一点的梯度（一个向量）；
显然，这个数学表达式是用泰勒公式展开得到的，对比自变量为一维的情况下的泰勒展开式：
f x k
f x f' x hoh
在目标函数值的数学表达式中，高阶无穷小可以忽略，因此，要使该式取到最小值，应使
取最小。 a
， b
)k T k
f x p
(
的夹角 的余弦定义为：
cos =
a
b
a b
假设向量 p 与负梯度 f(
)kx
的夹角是 ，我们便可求出点积 (
)k T k
f x p
的值为：
k
f x p f x
k T
) =-
(
(
)p cos
k
f x
(
) cos
可见， 为 0 时，上式取得最小值，也就是说，p 取 (
)kf x
时，目标函数下降得最快，
这就是称负梯度方向为“最速下降”方向的由来。
（四）最速下降法的收敛性以及收敛速度
最速下降法的收敛性：对一般的目标函数是整体收敛的，所谓整体收敛，是指不会非要在某
些点附近的范围内，才会有好的收敛性。最速下降法的收敛速度：至少是线性收敛的。
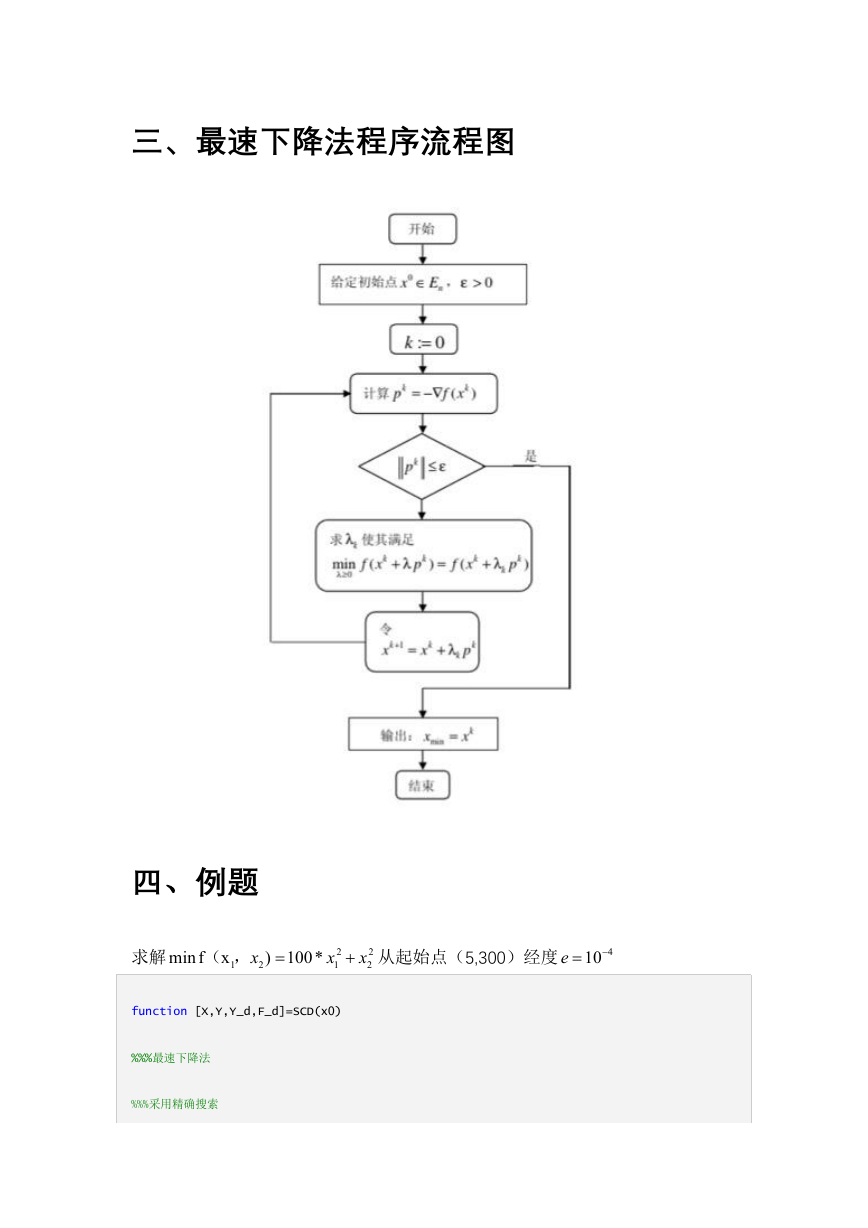
三、最速下降法程序流程图
四、例题
求解
minf x
（ ，
1
x
2
) 100*
2
x
1
x
2
2
从起始点（5,300）经度
e
410
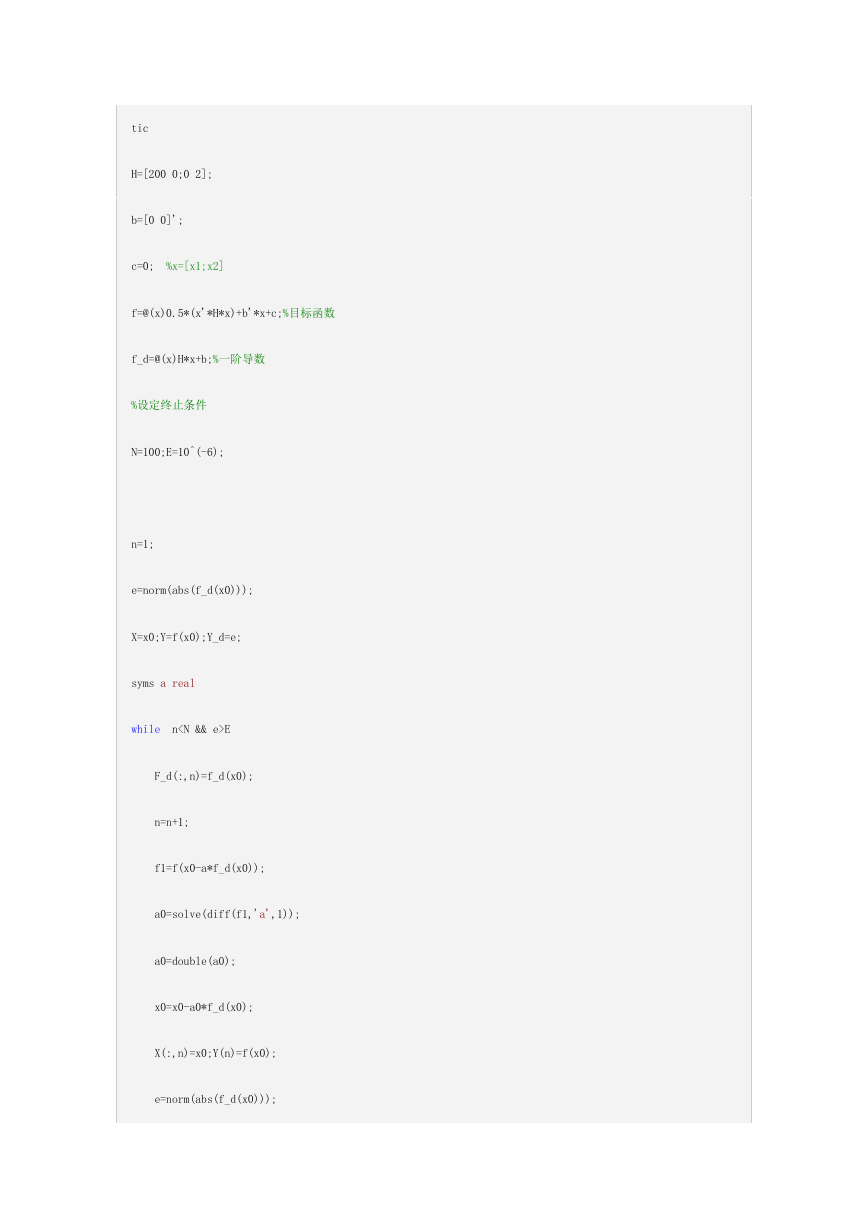
function [X,Y,Y_d,F_d]=SCD(x0)
%%%最速下降法
%%%采用精确搜索
tic
H=[200 0;0 2];
b=[0 0]';
c=0; %x=[x1;x2]
f=@(x)0.5*(x'*H*x)+b'*x+c;%目标函数
f_d=@(x)H*x+b;%一阶导数
%设定终止条件
N=100;E=10^(-6);
n=1;
e=norm(abs(f_d(x0)));
X=x0;Y=f(x0);Y_d=e;
syms a real
while nE
F_d(:,n)=f_d(x0);
n=n+1;
f1=f(x0-a*f_d(x0));
a0=solve(diff(f1,'a',1));
a0=double(a0);
x0=x0-a0*f_d(x0);
X(:,n)=x0;Y(n)=f(x0);
e=norm(abs(f_d(x0)));
Y_d(n)=e;
%F_d(:,n)=f_d(x0);
end
toc
figure(1)
subplot(2,1,1)
semilogy(Y,'r*')
title('best f(x)' )
ylabel('f(x)')
xlabel('iteration')
subplot(2,1,2)
semilogy(Y_d,'g<')
ylabel('f''(x)')
xlabel('iteration')
title(['beast fd' num2str(Y_d(n))])
figure(2)
x1=-20:1:20;y1=x1;
[X1 Y1]=meshgrid(x1,y1);
nn=length(x1);
Z1=zeros(nn,nn);
for i=1:nn
for j=1:nn
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
