logo资料库

常用弹塑性材料模型-常用弹塑性材料模型.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.09M 资料格式：doc 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    7.2.1.1各向同性弹性模型
    各向同性弹性模型。使用MP命令输入所需参数：
    此部分例题参看B.2.1，Isotropic Elastic Example:High Carbon
    B.2.1. Isotropic Elastic Example: High Carbon Stee
    B.2.7. Bilinear Isotropic Plasticity Example: Nick
    B.2.10. Bilinear Kinematic Plasticity Example: Tit
    B.2.11. Plastic Kinematic Example: 1018 Steel
    B.2.16. Piecewise Linear Plasticity Example: High
    B.2.25. Rigid Material Example: Steel
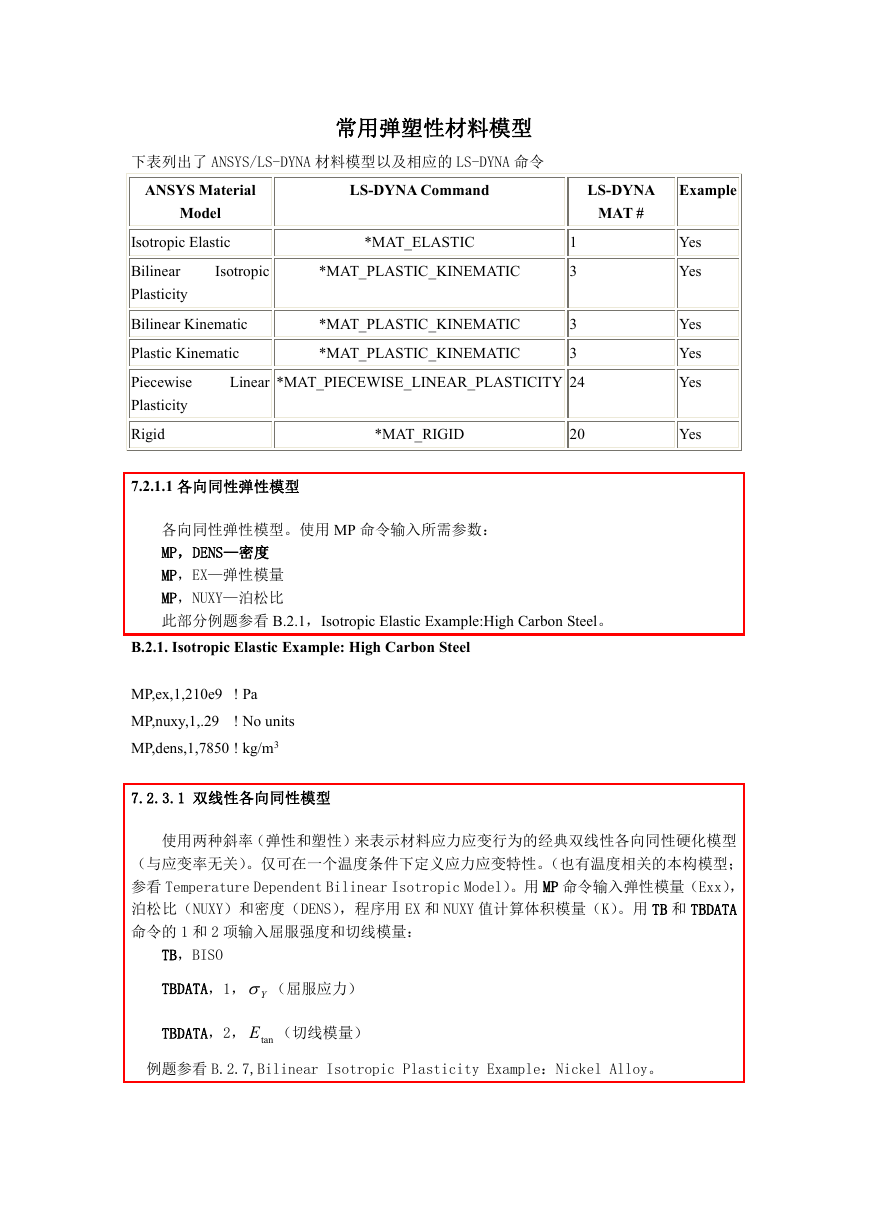
    常用弹塑性材料模型 下表列出了 ANSYS/LS-DYNA 材料模型以及相应的 LS-DYNA 命令 ANSYS Material LS-DYNA Command LS-DYNA Example Isotropic Model Isotropic Elastic Bilinear Plasticity Bilinear Kinematic Plastic Kinematic Piecewise Plasticity Rigid Linear *MAT_ELASTIC *MAT_PLASTIC_KINEMATIC 1 3 MAT # *MAT_PLASTIC_KINEMATIC *MAT_PLASTIC_KINEMATIC 3 3 *MAT_PIECEWISE_LINEAR_PLASTICITY 24 *MAT_RIGID 20 Yes Yes Yes Yes Yes Yes 7.2.1.1 各向同性弹性模型 各向同性弹性模型。使用 MP 命令输入所需参数： MP，DENS—密度 MP，EX—弹性模量 MP，NUXY—泊松比 此部分例题参看 B.2.1，Isotropic Elastic Example:High Carbon Steel。 B.2.1. Isotropic Elastic Example: High Carbon Steel MP,ex,1,210e9 ! Pa MP,nuxy,1,.29 ! No units MP,dens,1,7850 ! kg/m3 7.2.3.1 双线性各向同性模型 使用两种斜率（弹性和塑性）来表示材料应力应变行为的经典双线性各向同性硬化模型 （与应变率无关）。仅可在一个温度条件下定义应力应变特性。（也有温度相关的本构模型； 参看 Temperature Dependent Bilinear Isotropic Model）。用 MP 命令输入弹性模量（Exx）， 泊松比（NUXY）和密度（DENS），程序用 EX 和 NUXY 值计算体积模量（K）。用 TB 和 TBDATA 命令的 1 和 2 项输入屈服强度和切线模量： TB，BISO TBDATA，1， Y （屈服应力） TBDATA，2， tanE （切线模量） 例题参看 B.2.7,Bilinear Isotropic Plasticity Example：Nickel Alloy。
    B.2.7. Bilinear Isotropic Plasticity Example: Nickel Alloy ! Pa ! No units ! kg/m3 MP,ex,1,180e9 MP,nuxy,1,.31 MP,dens,1,8490 TB,BISO,1 TBDATA,1,900e6 ! Yield stress (Pa) TBDATA,2,445e6 ! Tangent modulus (Pa) 7.2.3.5 双线性随动模型 （与应变率无关）经典的双线性随动硬化模型，用两个斜率（弹性和塑性）来表示材料 的应力应变特性。用 MP 命令输入弹性模量（Exx），密度（DENS）和泊松比（NUXY）。可以用 TB，BKIN 和 TBDATA 命令中的 1-2 项输入屈服强度和切线模量： TB，BKIN TBDATA，1， Y （屈服应力） TBDATA，2， tanE （切线模量） 例题参看 B.2.10，Bilinear Kinematic Plasticity Example ：Titanium Alloy。 B.2.10. Bilinear Kinematic Plasticity Example: Titanium Alloy ! Pa ! No units ! kg/m3 MP,ex,1,100e9 MP,nuxy,1,.36 MP,dens,1,4650 TB,BKIN,1 TBDATA,1,70e6 ! Yield stress (Pa) TBDATA,2,112e6 ! Tangent modulus (Pa) 7.2.3.6 塑性随动模型 各向同性、随动硬化或各向同性和随动硬化的混合模型，与应变率相关，可考虑失效。 通过在 0（仅随动硬化）和 1（仅各向同性硬化）间调整硬化参数β来选择各向同性或随动 硬化。应变率用 Cowper-Symonds 模型来考虑，用与应变率有关的因数表示屈服应力，如下 所示：  Y    1            C     1 P       eff (  PP E  0 )
    这里 0 —初始屈服应力，  —应变率，C 和 P-Cowper Symonds 为应变率参数。 eff P — 有效塑性应变， PE —塑性硬化模量，由下式给出： EP  EE tan EE  tan 应力应变特性只能在一个温度条件下给定。用 MP 命令输入弹性模量（Exx），密度（DENS） 和泊松比（NUXY）。用 TB，PLAW，，，，1 和 TBDATA 命令中的 1-6 项输入屈服应力，切线斜率， 硬化参数，应变率参数 C 和 P 以及失效应变： 如下所示，可以用 TB，PLAW，，，，10 和 TBDATA 命令中的 1-5 项定义其它参数。 TB，PLAW，，，，1 TBDATA，1， Y （屈服应力） TBDATA，2， tanE （切线模量） TBDATA，3，β（硬化参数） TBDATA，4， C（应变率参数） TBDATA，5，P（应变率参数） TBDATA，6， f （失效应变） 例题参看 B.2.11，Plastic Kinematic Example：1018 Steel。 B.2.11. Plastic Kinematic Example: 1018 Steel ! Pa ! No units ! kg/m3 MP,ex,1,200e9 MP,nuxy,1,.27 MP,dens,1,7865 TB,PLAW,,,,1 TBDATA,1,310e6 ! Yield stress (Pa) TBDATA,2,763e6 ! Tangent modulus (Pa) TBDATA,4,40.0 ! C (s-1) TBDATA,5,5.0 TBDATA,6,.75 ! P ! Failure strain 7.2.3.13 分段线性塑性模型 多线性弹塑性材料模型，可输入与应变率相关的应力应变曲线。它是一个很常用的塑性 准则，特别用于钢。采用这个材料模型，也可根据塑性应变定义失效。采用 Cowper-Symbols 模型考虑应变率的影响，它与屈服应力的关系为：
     Y    1      &   C         1 P         0   P  eff f n   这里 ——有效应变率，C 和 P——应变率参数， 0 ——常应变率处的屈服应力，而 ( P nf  eff ) 是基于有效塑性应变的硬化函数。用 MP 命令输入弹性模量（Exx），密度(DENS)和泊松比 (NUXY)。用 TB，PLAW，，，，8 和 TBDATA 命令的 1-7 项输入屈服应力、切线模量、失效的有效 真实塑性应变、应变率参数 C、应变率参数 P、定义有效全应力相对于有效塑性真应变的载 荷曲线 ID 以及定义应变率缩放的载荷曲线 ID。 TB,PLAW,,,, 8 TBDATA,1, y （屈服应力） TBDATA,2, tanE （切线模量） TBDATA,3, F （失效时的有效塑性真应变） TBDATA,4,C（应变率参数） TBDATA,5,P（应变率参数） TBDATA,6,LCID1（定义全真应力相对于塑性真实应变的载荷曲线） TBDATA,7,LCID2（关于应变率缩放的载荷曲线） 注--如果采用载荷曲线 LCID1，则用 TBDATA 命令输入的屈服应力和切线模量将被忽略。 另外，如果 C 和 P 设为 0，则略去应变率影响。如果使用 LCID2，用 TBDATA 命令输入的应变 率参数 C 和 P 将被覆盖。只考虑真实应力和真实应变数据。在数据曲线一节中讲述了此种类 型的例题。 注--例题参看 B.2.16，Piecewise Linear Plasticity Example：High Carbon Steel。 B.2.16. Piecewise Linear Plasticity Example: High Carbon Steel ! Pa ! No units ! kg/m3 MP,ex,1,207e9 MP,nuxy,1,.30 MP,dens,1,7830 TB,PLAW,,,,8 TBDATA,1,207e6 ! Yield stress (Pa) TBDATA,3,.75 TBDATA,4,40.0 ! C (strain rate parameter) TBDATA,5,5.0 ! P (strain rate parameter) TBDATA,6,1 ! LCID for true stress vs. true strain (see EDCURVE below) *DIM,TruStran,,5 *DIM,TruStres,,5 TruStran(1)=0,.08,.16,.4,.75 ! Failure strain
    TruStres(1)=207e6,250e6,275e6,290e6,3000e6 EDCURVE,ADD,1,TruStran (1),TruStres(1) 7.2.8.1 刚性体模型 用 EDMP 命令定义刚性体，例如，定义材料 2 为刚性体，执行：EDMP，RIGIS，2。用指 定材料号定义的所有单元都认为是刚性体的一部分。材料号以及单元的单元类型和实常数类 型号用来定义刚体的 PART ID。这些 PART ID 用于定义刚性体的载荷和约束（如第 4 章所述， Loading）。刚体内的单元不必用连接性网格连接。因此，为了在模型中表示多个独立的刚性 体。必须定义多个刚体类型。但是，两个独立刚体不能共同使用一个节点。 使用 EDMP 命令的同时，必须用 MP 命令定义刚体材料类型的杨氏模量（Ex），泊松比（NUXY） 和密度（DENS）。必须指定实际的材料特性值，从而使程序能计算接触表面的刚度。基于此 原因，在显动态分析中，刚性体不要用不切实际的杨氏模量或密度，刚体不能再变硬因为它 已是完全刚硬的。 因为刚性体的质量中心的运动传递到节点上，所以不能用 D 命令在刚体上施加约束。刚 体的一个节点上的约束和初始速度将转换到物体的质心。但是，如果约束了多个节点，就很 难确定使用哪种约束。要正确在刚体上施加约束，使用 EDMP 命令的平移（VAL1）和转动（VAL2） 约束参数域，表示如下： VAL1-平移约束参数（相对于整体笛卡尔坐标系） 0 没有约束（缺省） 1 约束 X 方向的位移 2 约束 Y 方向的位移 3 约束 Z 方向的位移 4 约束 X 和 Y 方向的位移 5 约束 Y 和 Z 方向的位移 6 约束 Z 和 X 方向的位移 7 约束 X，Y，Z 方向的位移 VAL2-转动约束参数（相对于整体笛卡尔坐标系） 0 没有约束（缺省） 1 约束 X 方向的旋转 2 约束 Y 方向的旋转 3 约束 Z 方向的旋转 4 约束 X，Y 方向的旋转 5 约束 Y 和 Z 方向的旋转 6 约束 Z 和 X 方向的旋转 7 约束 X，Y 和 Z 方向的旋转 例如，命令 EDMP,IGID,2,7,7 将约束材料的刚体单元的所有自由度。 在定义刚体之后，可以用 EDIPART 命令指定惯性特性、质量和初始速度矢量。如果没有 定义刚性体的惯性特性，程序将会依据有限元模型计算它们。 例题参看 B.2.25,Rigid Material Example：Steel。 B.2.25. Rigid Material Example: Steel MP,ex,1,207e9 ! Pa
    ! No units MP,nuxy,1,.3 MP,dens,1,7580 ! kg/m3 EDMP,rigid,1,7,7
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料