第 30 卷第 11 期 　　　　　　　　　应 　　　用 　　　科 　　　技 　　　　　　　　　Vol. 30 , №. 11 2003 年 11 月 　　　　　　　　　Applied 　Science 　and 　Technology 　　　　　　　 　　Nov. 2003 文章编号 :1009 - 671X(2003) 11 - 0031 - 03 m 序列优选对及平衡 Gold 序列的产生与搜索 闫保中 , 何联俊 , 洪 　艳 (哈尔滨工程大学 自动化学院 ,黑龙江 哈尔滨 　150001) 摘 　　　要 :扩频通信系统需要相关性好的扩频码 ,因此 ,在分析 m 序列优选对 ,平衡 Gold 序列的产生方法和 相关特性基础上 ,提出了一种采用 C 语言搜索 m 优选对和平衡 Gold 序列的计算机实现方法 ,给出了搜索程序 流程图. 该方法可以正确 、快速地完成平衡 Gold 码的搜索 ,对扩频码的优选具有参考价值. 关 　键 　词 :扩频通信 ;m 序列 ; Gold 序列 ;程序流程图 中图分类号 : TN914. 4 　文献标识码 :A Generation and selection of m sequence pairs and balanced Gold sequence YAN Bao-zhong ,HE Lian-jun ,HON G Yan (School of Automation , Harbin Engineering University , Harbin 150001 , China) Abstract :Spread spectrum communication system needs spread sequences wit h good correlation. On t he ba sis of analyzing t he generating ways and t he correlation performance of m sequences optimum pairs and bal anced Gold sequences ,t he computer realization of how to get t hem wit h C language was presented , and t he program flow charts were provided. A correct balanced Gold sequence can be accomplished quickly by t his means. The paper is a useful reference for surveying spread sequences. Key words :spread spectrum communication ; m sequence ; Gold sequence ; program flow chart 　　扩频通信的抗干扰 、抗噪声 、信息数据保密 、 多址通信 、捕获与跟踪都与扩频码的设计密切相 关 ,因此对扩频码的研究就变得十分重要. m 序列 具有良好的自相关特性 ,但可用的地址数较少 ,容 易被窃获 ,因而其应用受到一定的限制. 由 2 个 m 序列优选对复合而成的 Gold 码具有优越的相关 特性 ,而且两两互相关函数小的序列数量较多 ,因 此被广泛采用. 但在 Gold 序列族中 ,往往只有平 衡 Gold 序列被采纳 ,因此需采取有效措施搜索平 衡 Gold 序列. 文献[ 4 ]从理论上给出了一种平衡 Gold 序列 的搜索算法 ,但比较复杂. 本文在分析了 Gold 序 列产生方法的基础上 ,提出了一种利用 C 语言搜 索 m 序列优选对及平衡 Gold 序列的计算机实现 方法. 该算法简单 ,运算速度快 ,在无线电导航系 统测距地址码的优选中发挥重要作用. 1 　m 序列及 m 序列优选对 m 序列由 n 级线性反馈移位寄存器构成 ,如 图 1 所示. 图 1 　n 级线性反馈移位寄存器原理图 m 序列的周期 P 必须满足 P = 2 n - 1 ,其结构 中的第一级与第 n 级必须有反馈作用 ,即反馈系 数 c0 = cn = 1. 线性移位寄存器的反馈系数可用特 征多项式来描述 ,即 f ( x ) = c0 + c1 x + ……+ cn x n ,其中 x i 存在表明 ci = 1 ,否则 ci = 0 , ci 的取 值决定了移位寄存器的反馈连线. 也可利用八进制 数形式来描述 ,比如(5411) 8 描述的是 11 级线性移 位寄存器的特征多项式 : f ( x ) = x11 + x9 + x8 + x3 + 1. 已经证明只有不可约多项式中的本原多项 式才能够产生 m 序列. 详细内容参阅文献[2 ]. m 序列具有良好的自相关特性. 序列的自相 关和互相关是当两个序列逐位比较时 ,一致的数 目( A ) 减去不一致的数目 ( D) ,即 R (τ) = A - 收稿日期 :2002 - 12 - 25. 作者简介 :闫保中 (1966 - ) ,男 ,副研究员 ,主要研究方向 :导航、制导与控制. © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

Π Π Π Π ·23· 应 　　　用 　　　科 　　　技 　　　　　　　　　　　　第 30 卷 D . 在 0 位移和比特位移之间的区域 ,相关值是线 性增加的 ,所以 m 序列的自相关函数是如图 2 所 示的三角形. 一个新的 Gold 序列. Gold 序列继承了 m 序列优选对的相关特性 , 也具有三值性 ,而且可以用作地址码的数量比 m 序列要多得多. 对于 2 个 n 级线性移位寄存器 , 当相对位移 ( 2 n - 1) 比特时 , 就可以得到一族 (2 n - 1)个 Gold 序列 ,再加上两个 m 序列 ,共有 (2 n + 1) 个 Gold 序列. Gold 序列已经不再是 m 序 列 ,也就不满足 m 序列在每一个周期内“1”出现 的次数比“0”多一次的特性 ,因此在应用 Gold 码 作为扩频序列时 ,必须研究 Gold 码的平衡性. 因 为在扩频系统中 ,对系统性能的影响之一就是码 的平衡性 ,不平衡码将使扩频系统载波泄露增大 , 破坏扩频系统的保密 、抗干扰和抗侦破能力. 平衡 Gold 序列中“1”的个数比“0”的个数多 一个. 由文献 [ 3 ]获知 ,当 n 为奇数时 ,平衡码和 非平衡码出现的概率各占 50 % ;当 n 为偶数 (但 不为 4 的倍数) 时 ,平衡码出现的概率为 75 % ,非 平衡码为 25 %. 3 　程序搜索实现 3. 1 　m 序列优选对 n 级线性移位寄存器要产生 m 序列 ,其连接 多项式必须是本原多项式. 以 11 级线性移位寄存 器为例 ,其一个八进制本原多项式为 (5411) 8 ,用 二进制表示为 (101100001001) 2 ,通过位移的方式 可将该本原多项式转存到数组 C[ 12 ]中 ,存放的 格式为 C[ 12 ] = {1 ,0 ,1 ,1 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,1} ,其 中元素 C[ i ]代表反馈系数 ci ,元素 C[ i ]为 1 则 表示对应的反馈系数 ci 为 1. 移位寄存器中的状 态也用数组表示 ,如 11 级移位寄存器的状态为 “11011111001”时 ,其数组表示形式为 a [ 11 ] = {1 ,1 ,0 ,1 ,1 ,1 ,1 ,1 ,0 ,0 ,1}. 根据反馈系数 ,采用 逐步移位模二加算法来寻找 m 序列优选对. 逐步 移位模二加算法是将要计算的 m 序列族中某 2 个序列之一固定 ,另一 m 序列逐步循环移位 ,每 移动一步将得到一个新的 m 序列. 移动 τ( 0 < τ≤2 n - 1) 位后 ,将此被移位后的序列与固定序 列各码元对应位做比较 ,计算 A 和 D ,进而得到 m 序列延迟 τ位时的互相关函数. 若此相关函数 值满足公式 (1) 的理论界限值 ,则这两个 m 序列 就是 m 序列优选对 ,否则就不是 m 序列优选对. 图 4 给出了 m 序列优选对程序流程. 3. 2 　平衡 Gold 序列 m 序列优选对的初始状态不同 ,得到的 Gold 序列也不同 ,因此需确定移位寄存器哪些初始状态 图 2 　m 序列自相关函数 m 序列具有下列性质 : (1) 在序列中“1”的数 目和“0”的数目只相差一个比特 ; (2) m 序列相移 后和 m 序列本身做模二加所得到的序列还是 m 序列 ,只不过与原来的两个 m 序列相移不同而 已 ; (3) 游程分布的随机性 ,长度为 K 的游程个数 占游程总数的 1 2 k ,其中 1 ≤k ≤( n - 2) . 而且 , 在长度为 K 的游程中 ,连 1 游程与连 0 游程各占 一半 ,长为 ( n - 1) 的游程是连 0 游程 ,长为 n 的 游程是连 1 游程. m 序列优选对的定义为 :设 A 是对应于 n 级 本原多项式 f ( x ) 所产生的 m 序列 , B 是对应于 n 级本原多项式 g ( x ) 所产生的 m 序列 ,当它们的 互相关函数| R a , b ( k) | 满足 : n+1 n+2 2 2 = Ra , b ( k) 2 + 1 , n 为奇数 2 + 1 , n 为偶数 ,且 n 不为 4 的倍数 (1) 则 f ( x) 和 g ( x) 所产生的 m 序列 A 和 B 构成一 对优选对. m 序列优选对的互相关和自相关函数 具有三值性 :当 n 为奇数时 ,互相关函数 R (τ) 取 值为 - 1 、- (2 ( n + 1) 2 - 1) ;当 n 为偶 数 ,且不为 4 的倍数时 ,互相关函数 R (τ) 取值为 - 1 、- (2 ( n + 2) 2 - 1) . 2 　Gold 码及平衡 Gold 码 2 + 1) 、(2 ( n + 1) 2 + 1) 、(2 ( n + 2) Gold 码是由 2 个码长相等 、码时钟速率相同 的 m 序列优选对模二加和构成 ,其产生方法如图 3 所示. 每改变 2 个 m 序列相对位移就可以得到 图 3 　Gold 码产生器原理图 © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

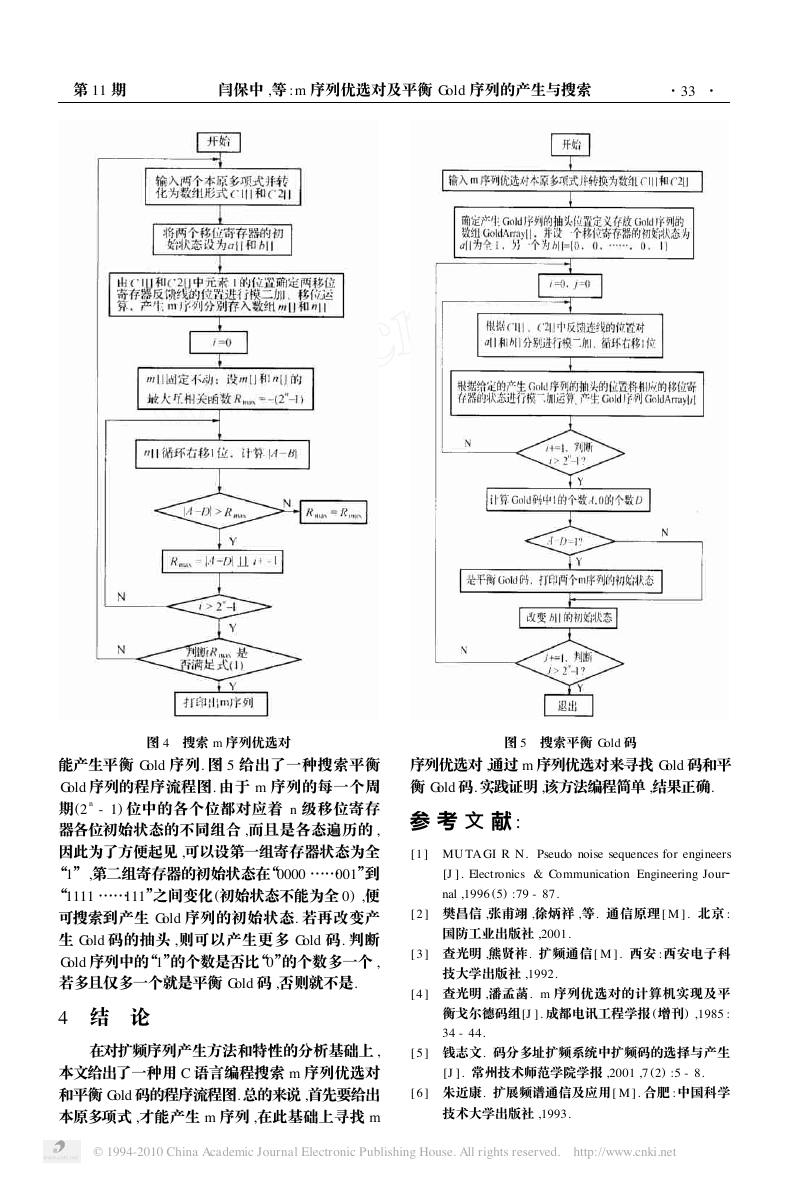
2 第 11 期 　　　　　　闫保中 ,等 :m 序列优选对及平衡 Gold 序列的产生与搜索 ·33· 图 4 　搜索 m 序列优选对 图 5 　搜索平衡 Gold 码 能产生平衡 Gold 序列. 图 5 给出了一种搜索平衡 Gold 序列的程序流程图. 由于 m 序列的每一个周 期(2 n - 1) 位中的各个位都对应着 n 级移位寄存 器各位初始状态的不同组合 ,而且是各态遍历的 , 因此为了方便起见 ,可以设第一组寄存器状态为全 “1”,第二组寄存器的初始状态在“0000 ……001”到 “1111 ……111”之间变化(初始状态不能为全 0) ,便 可搜索到产生 Gold 序列的初始状态. 若再改变产 生 Gold 码的抽头 ,则可以产生更多 Gold 码. 判断 Gold 序列中的“1”的个数是否比“0”的个数多一个 , 若多且仅多一个就是平衡 Gold 码 ,否则就不是. 4 　结 　论 在对扩频序列产生方法和特性的分析基础上 , 本文给出了一种用 C 语言编程搜索 m 序列优选对 和平衡 Gold 码的程序流程图. 总的来说 ,首先要给出 本原多项式 ,才能产生 m 序列 ,在此基础上寻找 m 序列优选对 ,通过 m 序列优选对来寻找 Gold 码和平 衡 Gold 码. 实践证明 ,该方法编程简单 ,结果正确. 参 考 文 献 : [1 ] 　MU TA GI R N. Pseudo noise sequences for engineers [J ]. Electronics & Communication Engineering Jour nal ,1996 (5) :79 - 87. [2 ] 　樊昌信 ,张甫翊 ,徐炳祥 ,等. 通信原理 [ M ]. 北京 : 国防工业出版社 ,2001. [3 ] 　查光明 ,熊贤祚. 扩频通信 [ M ]. 西安 :西安电子科 技大学出版社 ,1992. [4 ] 　查光明 ,潘孟菡. m 序列优选对的计算机实现及平 衡戈尔德码组[J ]. 成都电讯工程学报 (增刊) ,1985 : 34 - 44. [5 ] 　钱志文. 码分多址扩频系统中扩频码的选择与产生 [J ]. 常州技术师范学院学报 ,2001 ,7 (2) :5 - 8. [6 ] 　朱近康. 扩展频谱通信及应用 [ M ]. 合肥 :中国科学 技术大学出版社 ,1993. © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net