http://www.paper.edu.cn 基于 MATLAB 的线性二次型最优控制设计 王国星 西北工业大学自动化学院，陕西西安(710129) E-mail: wangguoxing@mail.nwpu.edu.cn 摘 要： 本文介绍了线性二次型最优控制的基本原理，并给定了一个具体的控制系统，利 用 MATLAB 软件对其最优控制矩阵进行了求解，最后用 SIMULINK 对所给定的系统进行 了仿真，通过仿真实验，设计所得到的线性二次型最优控制效果比较好，达到了设计的目的。 关键词：MATLAB; 线型二次型；最优控制；SIMULINK 中图分类号：TP391 1. 引 言 文献标识码：A 最优控制问题就是寻找一个控制系统的最优控制方案或最优控制规律，使系统能最优地 达到预期的目标。以状态空间理论为基础的最优控制算法是当前振动控制中采用最为普遍的 控制器设计方法。本文所讨论的系统是完全可观测的，所以可以用线性二次型最优控制。 2. 最优控制理论介绍 假设线性时不变系统的状态方程模型为[1] x‘(t)=Ax(t)+Bu(t) y(t)=Cx(t)+Du(t) 引入一个最优控制的性能指标，即设计一个输入量 u,使得 J = 为最小。其中Q和R分别为对状态变量和输入变量的加权矩阵; tf为控制作用的终止时间。矩 阵S对控制系统的终值也给出某种约束，这样的控制问题称为线性二次型（Linear Quadratic， 简称LQ）最优控制问题。 为了求解 LQ 问题，我们取 Hamilton 函数[1] ( )) ( ), H t x t u t t  ( ) ( ) ( ) t Q t x t  并应用变分原理推导出 问题解满足的必要条件： ( )( ( ) ( ) t A t x t ( ) t R t u t LQ B t u t ( ) ( )); ( , 0.5( ( ) ( )) ( ), x T  T    T u  ( ) t   H     ( ( ) ( ) Q t x t  ( ) A t  ( )); t H  u  ' ( ) x t  0( ( ) ( ) Q t x t  ( ) A t  ( ))); t  ( ) ( ) A t x t  B t u t ( ) ( ); 其中一种较为简便的解法为： 令(t)=P(t)x(t) 而将对(t)的求解转化到对函数矩阵 P(t)的求解`，特别的，将(t)=P(t)x(t)代入上述式子 - 1 - 

http://www.paper.edu.cn  中可得函数矩阵 P(t)因满足的微分方程是 '( ) ( ) ( ) P t A t P t   ) . ( S P tf  对它的求解可应用成熟的Euler方法。假定方程(1)的唯一对称半正定解P(t),则LQ问题的解u(t) 由下式给出： ( ) ( ); P t B t R t B t P t Q t T ( ) A t P t ( ) ( ) ( ) ( ) ( ) (1)   1  T 1 ( ) ( ).  R t B t P t x t ^ ( ) u t 上述 问题的一个特例是动态方程为定常的情形，即 ( ) ( )   LQ T 相应的控制向量取为 （ u t)=-Kx(t). 其中， 为才是矩阵，而二次性能指标为 K   J= ( 0 T ( ) x t Qx t ( )  T u t Ru t dt ( )) ( ) . 这里 和 是给定的实对称正定 或半正定 矩阵 ，它们规定了误差和控制信号能量 ( ) ` Q R 消耗的模式，在这特别的情形，我们可求出 -1 T K=R B P 这里 满足方程： 1 T  A P PA PBR B P Q 的唯一对称半正定矩阵解 P  0;    T 3. 问题的阐述与解决 3.1.问题的阐述： 0 2 2 2 [ x   x 1 )( t )( t )] dt 2 ( tu   J 极小[1]，并运用 SIMULINK 仿真，输出 x1、x2、J 的波形。 3.2.问题的求解： 根据系统的状态空间方程，可以看出 A=[0 1;0 0], B=[0;1], Q=[1 0;0 1], R=[1]。 控制系统工具箱供了 lqr( )函数[4]，用来依照给定的加权矩阵设计 LQ 最优控制器,该函 数的调用格式为 : [K,P]=lqr(A,B,Q,R) 式中：（A,B）为给定的的对象状态方程模型；（Q,R）分别为加权矩阵 Q 和 R;返回的 向量 K 为状态反馈向量,也就是控制器,P 为 Riccati 代数方程的解。 在本题中，可用下面的 MATLAB 代码求解 K 和 P: clear A=[0 1;0 0]; B=[0;1]; - 2 - 

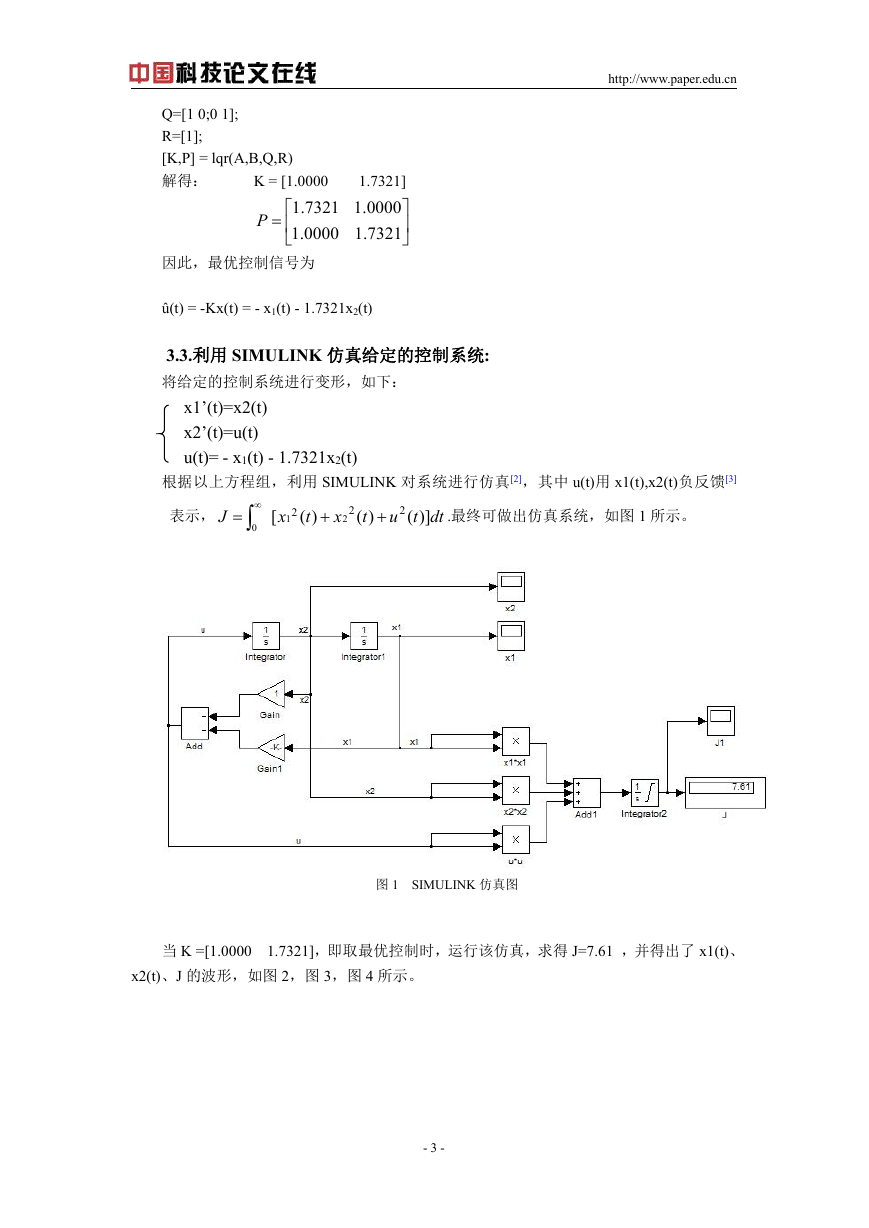
Q=[1 0;0 1]; R=[1]; [K,P] = lqr(A,B,Q,R) 解得： K = [1.0000 7321 0000 P .1   .1  因此，最优控制信号为  http://www.paper.edu.cn 1.7321] .1 0000   .1 7321  û(t) = -Kx(t) = - x1(t) - 1.7321x2(t) 3.3.利用 SIMULINK 仿真给定的控制系统: 将给定的控制系统进行变形，如下： x1’(t)=x2(t) x2’(t)=u(t) u(t)= - x1(t) - 1.7321x2(t) 根据以上方程组，利用 SIMULINK 对系统进行仿真[2]，其中 u(t)用 x1(t),x2(t)负反馈[3] 表示， J   0 [ x 1 2 )( t  x 2 2 )( t  2 ( tu )] dt .最终可做出仿真系统，如图 1 所示。 根据状态空间方程，利用 SIMULINK 可画出如图 1 所示的仿真图。 图 1 SIMULINK 仿真图 当 K =[1.0000 1.7321]，即取最优控制时，运行该仿真，求得 J=7.61 ，并得出了 x1(t)、 x2(t)、J 的波形，如图 2，图 3，图 4 所示。 - 3 - 

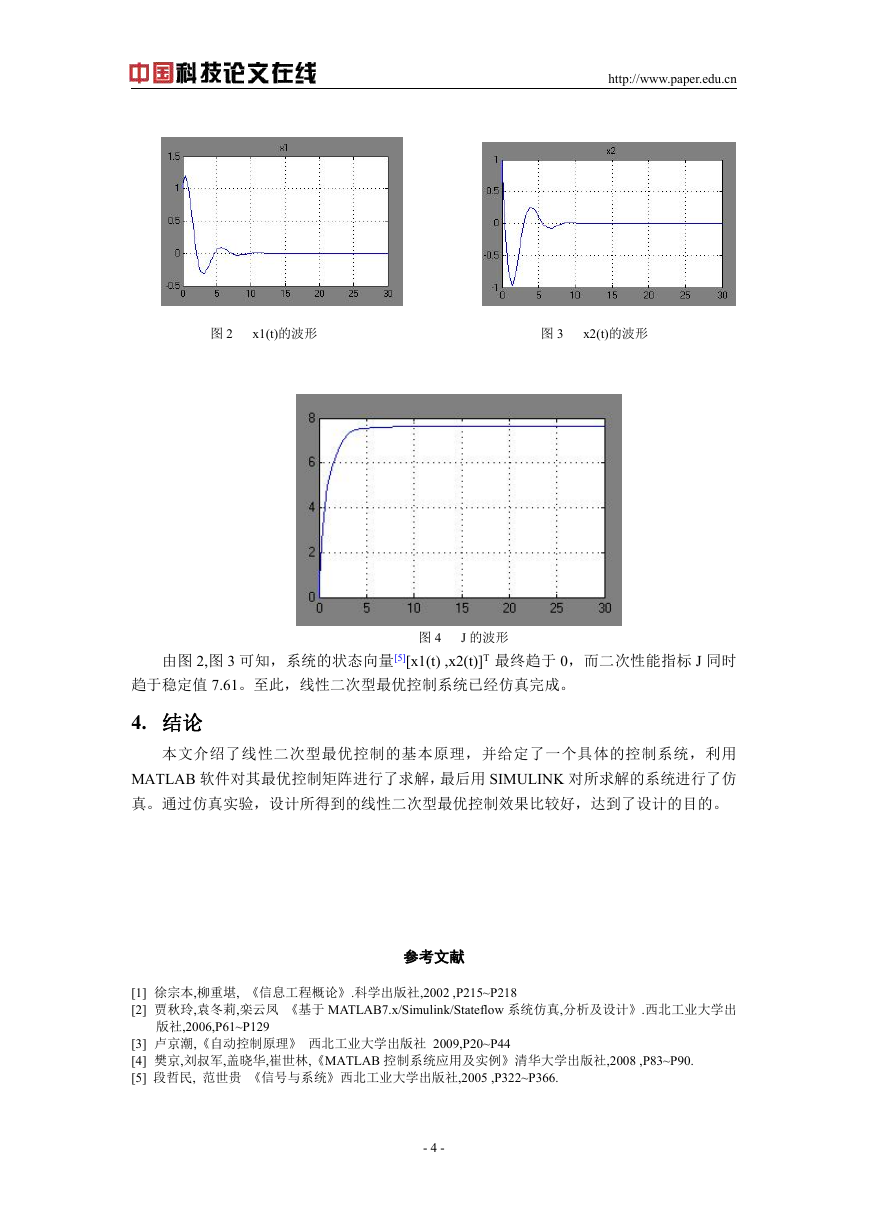
http://www.paper.edu.cn 图 2 x1(t)的波形 图 3 x2(t)的波形 由图 2,图 3 可知，系统的状态向量[5][x1(t) ,x2(t)]T 最终趋于 0，而二次性能指标 J 同时 图 4 J 的波形 趋于稳定值 7.61。至此，线性二次型最优控制系统已经仿真完成。 4. 结论 本文介绍了线性二次型最优控制的基本原理，并给定了一个具体的控制系统，利用 MATLAB 软件对其最优控制矩阵进行了求解，最后用 SIMULINK 对所求解的系统进行了仿 真。通过仿真实验，设计所得到的线性二次型最优控制效果比较好，达到了设计的目的。 参考文献 [1] 徐宗本,柳重堪, 《信息工程概论》.科学出版社,2002 ,P215~P218 [2] 贾秋玲,袁冬莉,栾云凤 《基于 MATLAB7.x/Simulink/Stateflow 系统仿真,分析及设计》.西北工业大学出 版社,2006,P61~P129 [3] 卢京潮,《自动控制原理》 西北工业大学出版社 2009,P20~P44 [4] 樊京,刘叔军,盖晓华,崔世林,《MATLAB 控制系统应用及实例》清华大学出版社,2008 ,P83~P90. [5] 段哲民, 范世贵 《信号与系统》西北工业大学出版社,2005 ,P322~P366. - 4 - 

http://www.paper.edu.cn Linear Quadratic Optimal Control Design Based On MATLAB Wang Guoxing College of Automation, Northwestern Polytechnical University, Xi 'an, PRC(710129) Abstract This paper describes the basic principles of the linear quadratic optimal control, and gives a specific control system, then solves the matrix of optimal control with MATLAB, and finally simulate the system with SIMULINK. Through simulation, the effect of the linear quadratic optimal control we designed is good, achieving the design objective. Keywords: MATLAB; Linear quadratic; Optimal Control; SIMULINK - 5 -