第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
关键词唤醒卷积神经网络算法.docx
本文中我们将探寻使用卷积神经网络（CNNs）来进行短句的关键字识别（KWS）的方
法。CNNs 在 KWS 的应用中很有前景，因为它的参数要比 DNNs 好得多。在接下来的工作
中引入了两种不同的方式，一种是限制 KWS 系统的乘法数量，另一种是限制参数的数量。
我们提供新的 CNN 架构来解决每个应用程序的约束。我们发现，与 DNN 相比，CNN 的架
构提供了 27%-44%的错误拒绝率，同时也适应了每个应用程序的约束条件。
1. 概述
随着移动设备的快速发展，语音相关技术正变得越来越流行。例如，谷歌提供了在
Android 手机上使用语音[1]进行搜索的功能，而谷歌的 Now、苹果的 Siri、微软的 Cortana
和亚马逊的 Alexa 等个人助理都利用语音识别技术与这些系统进行互动。谷歌已经启用了完
全免提语音识别体验，即“Ok Google”2，它不断地监听特定的关键词来启动语音输入。这
个关键字识别（KWS）系统在移动设备上运行，因此必须有一个小的内存占用和低的计算
能力。
Google [2]的 KWS 系统使用了一个深度神经网络（DNN），它被训练来预测子关键字目
标。事实证明，DNN 的表现优于 KWD/Filler 的 HMM 系统，这是一种常用的关键字识别技
术。此外，DNN 在设备上运行是有吸引力的，因为可以通过改变网络中参数的数量来轻松
地调整模型的大小。
然而，我们相信替代的神经网络体系结构可能为我们的 KWS 任务提供进一步的改进。
具体地说，卷积神经网络（CNNs）[3]在过去的几年中已经很流行了，它显示了在各种各样
的小而大的词汇任务[4,5,6]中对 DNNs 的改进。
由于各种原因，CNNs 与 DNNs 相比具有吸引力。首先，DNNs 忽略输入拓扑，因为输
入可以在任何（固定）顺序中显示，而不会影响网络[3]的性能。然而，语音的光谱表示在
时间和频率上具有很强的相关性，并且通过在输入空间的局部区域中共享的权重来建模与
CNNs 的局部相关性，在其他领域中已经被证明是有益的。其次，DNNs 并没有明确地设计
成在语音信号中对平动方差进行建模，因为不同的说话方式可以存在。更具体地说，不同的
说话方式导致了在频域内发生位移。这些演讲风格要求我们应用各种各样的说话者适应技术
来减少特征的变化。虽然足够大小的 DNNs 确实能够捕获平移不变性，但这需要有大量训
练样本的大型网络。另一方面，CNNs 通过在不同的本地时间和频率区域中平均输出隐藏单
元的输出来捕获转化的不变性。
我们有动力去看 CNNs 的 KWS，因为 CNNs 在改进性能和减少模型尺寸[4,5,6]的情况
下，已经显示出了 CNNs 的好处。在本文中，我们讨论了 CNNs 的两个应用程序。首先，我
们考虑的问题是，我们必须限制我们的 KWS 系统的总体计算，即参数和乘法。有了这个限
制，典型的体系结构在频率上只有 8 个，在这里是不能用的。因此，我们引入了一种新颖的
CNN 架构，它不需要池，而是在频率上大步前进，以在计算约束问题中。其次，我们考虑
限制我们的 KWS 系统的参数总数。对于这个问题，我们展示了我们可以通过在时间和频率
上的聚集来提高性能，第一次在没有使用多个卷积块[5、9]的情况下，这已经被证明是有效
的。
我们在 KWS 任务中评估我们提出的 CNN 架构，它包含 14 个不同的短语。性能是通过
在每小时 1 个假警报（FA）的操作阈值中观察错误的拒绝（FR）率来衡量的。在我们限制
乘法的任务中，我们发现一个在频率上跨步的 CNN，在相对于 DNN 的基础上，提供了超过
27%的相对改进。此外，在限制参数的任务中，我们发现 CNN 在时间上的缓冲时间比传统
的 CNN 和传统的 CNN 只在频率上增加了 41%，而传统的 CNN 只有 6%。
本文的其余部分如下所列。在第 2 部分中，我们概述了本文中使用的 KWS 系统。第 3
部分介绍了我们在限制计算和参数时探索的不同的 CNN 架构。第 4 节描述了实验设置，而
比较 CNN 和 DNN 的结果则在第 5 部分中介绍。最后，第 6 节总结了这篇论文，并讨论了
未来的工作。
2. 关键词唤醒
图 1 展示了在这个工作中使用的 DNN KWS 系统[2]的框图。从概念上讲，我们的系统
由三个组件组成。首先，在特征提取模块中，40 维的 log-mel filterbank 特性每 25 毫秒计算
一次，并有 10 ms 的帧频移。接下来，在每一帧中，我们将 23 帧叠加到左边，右边是 8 帧，
然后将其输入到 DNN 中。
基线 DNN 架构由 3 个隐藏层组成，其中有 128 个隐藏单元/层和一个 softmax 层。每个
隐藏层使用一个整流的线性单元（ReLU）非线性。将 softmax 输出层包含一个输出目标为
每个关键词组中的词被探测到,加上一个额外的输出目标代表的所有帧，不属于任何关键字
中的词(表示为图 1 中“填料”)。训练网络权值优化熵准则使用分布式异步梯度下降[10]。
最后，在后处理模块中，来自 DNN 的单个帧级后分数被组合成一个与关键字对应的分数。
关于这三个模块的更多细节，我们请读者参阅[2]。
图 1：深度 KWS 系统的框架，从左到右的：(i)特征提取(ii)深度神经网络(iii)后置处理
3. CNN 架构
在本节中，我们将 CNN 架构描述为第二节中描述的 DNN 的替代方案。特征提取和后
处理阶段与第 2 部分相同。
3.1 CNN 概述
典型的 CNN 架构如图 2 所示。首先，我们得到一个输入信号
，其中 t 和 f 分
别是时间和频率的输入特性维度。一个权重矩阵
与完整的输入 V 进行卷积。
权重矩阵跨越了一个小的本地时间频率的小块 m×r，在这个小范围内，m<=t 和 r<=f。这个
权重的分享有助于在输入信号中模拟局部相关性。权重矩阵有 n 个隐藏单元（如特征图谱)。
这个过滤器可以在时间和频率上以非零的速度前进。因此，总的来说，卷积操作产生了大小
的 n 个特征图。
在执行卷积之后，一个 max-池层有助于消除由于说话方式、通道失真等原因而存在的
时间频率空间的可变性。考虑到 p×q 的池大小，池执行一个次采样操作来减少时间频率空
间。出于本文的目的，我们考虑的是不重叠的池，因为它没有显示对语音[8]有帮助。在池
之后，时间频率空间有维度
。
图 2：图展示了一个典型的卷积网络体系结构，由卷积和 max-合用层组成。
3.2 典型的卷积架构
一个典型的卷积架构，经过了严格的测试，并显示在许多 LVCSR 任务中很好地工作
[6,11]，是使用两个卷积层。假设 log-mel 在 CNN 的输入是 t×f=32×40，那么通常第一层的
频率是 r=9 的频率。该体系结构对滤波器的大小不太敏感，尽管通常的做法是在时间内选择
一个过滤大小，它的时间跨度为 2/3，即 m=20。卷积运算是通过在时间和频率上跨越 s=1
和 v=1 来完成的。其次，在频率上只执行不重叠的 max-pooling，并带有 q=3 的池区域。第
二个卷积滤波器的频率是 r=4 的过滤器大小，并且不执行任何 max-pooling。
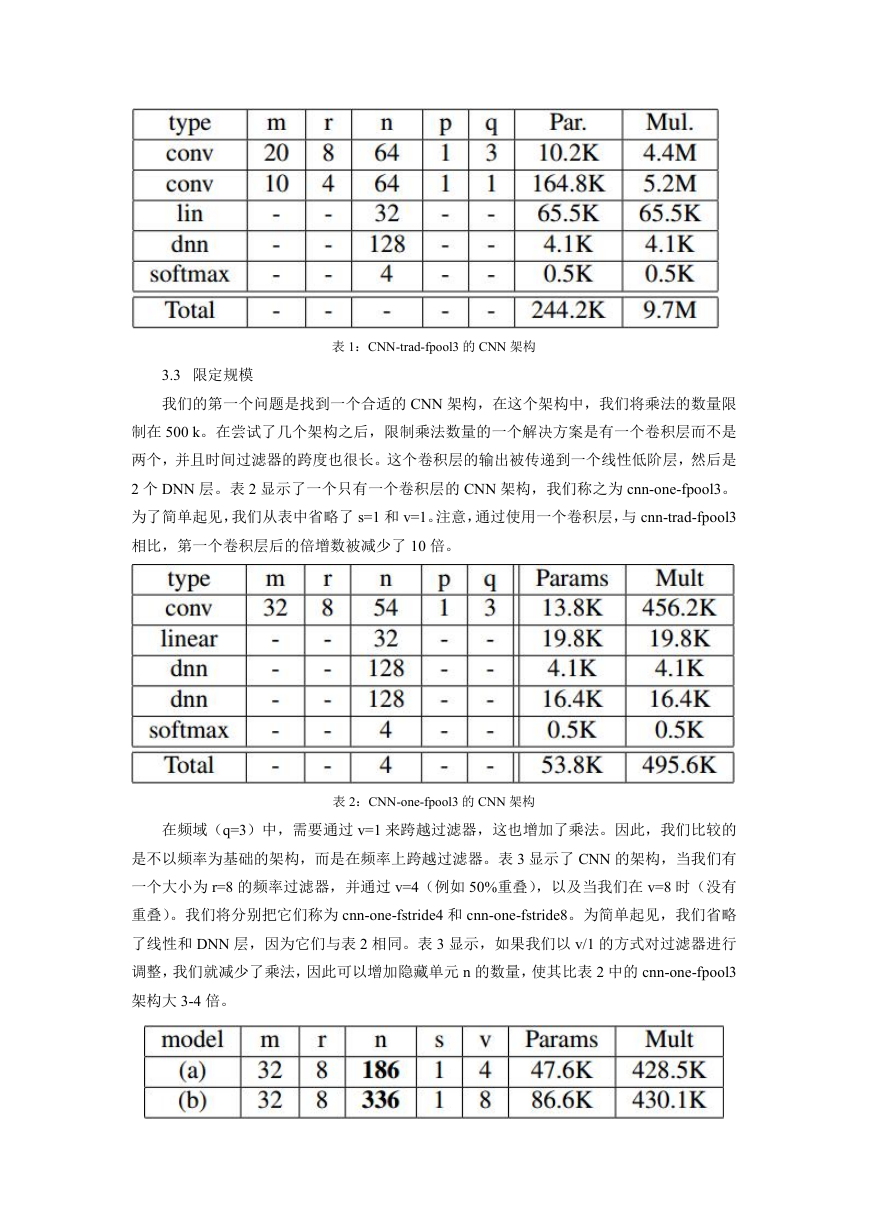
例如，在我们的任务中，如果我们想要将参数的数量保持在 250 K 以下，那么一个典型
的 CNN 架构就如表 1 所示。在本文中，我们将把这个体系结构称为 cnn-trad-fpool3。这个
体系结构有两个卷积，一个线性低阶和一个 DNN 层。在第 5 部分中，我们将向 KWS 展示
这种体系结构的好处，特别是在频率上的池，与 DNN 相比。
然而，这个体系结构的一个主要问题是在卷积层中有大量的乘法，由于三维的输入，跨
越时间、频率和特征映射，在第二层中会加剧。这种类型的体系结构不适合在有限的情况下，
在有限的情况下，小型的 KWS 任务是有限的。此外，即使我们的应用程序受到参数的限制，
也不会被复制，但是其他的架构在时间上可能更适合 KWS。下面我们介绍了可选择的 CNN
架构，以解决限制参数或相乘的任务。
表 1：CNN-trad-fpool3 的 CNN 架构
3.3 限定规模
我们的第一个问题是找到一个合适的 CNN 架构，在这个架构中，我们将乘法的数量限
制在 500 k。在尝试了几个架构之后，限制乘法数量的一个解决方案是有一个卷积层而不是
两个，并且时间过滤器的跨度也很长。这个卷积层的输出被传递到一个线性低阶层，然后是
2 个 DNN 层。表 2 显示了一个只有一个卷积层的 CNN 架构，我们称之为 cnn-one-fpool3。
为了简单起见，我们从表中省略了 s=1 和 v=1。注意，通过使用一个卷积层，与 cnn-trad-fpool3
相比，第一个卷积层后的倍增数被减少了 10 倍。
表 2：CNN-one-fpool3 的 CNN 架构
在频域（q=3）中，需要通过 v=1 来跨越过滤器，这也增加了乘法。因此，我们比较的
是不以频率为基础的架构，而是在频率上跨越过滤器。表 3 显示了 CNN 的架构，当我们有
一个大小为 r=8 的频率过滤器，并通过 v=4（例如 50%重叠），以及当我们在 v=8 时（没有
重叠）。我们将分别把它们称为 cnn-one-fstride4 和 cnn-one-fstride8。为简单起见，我们省略
了线性和 DNN 层，因为它们与表 2 相同。表 3 显示，如果我们以 v/1 的方式对过滤器进行
调整，我们就减少了乘法，因此可以增加隐藏单元 n 的数量，使其比表 2 中的 cnn-one-fpool3
架构大 3-4 倍。
表 3：(a) cnn-one-fstride4 以及(b) cnn-for-fstride8 的 cnn
3.4 极限参数
在上一节中介绍的模型的一个问题是，当保持不变时，模型的参数数量仍然比 250 k 小
得多。然而，增加 CNN 的参数通常会带来进一步的改进。在其他应用程序中，我们希望设
计一个模型，在这个模型中，我们保留了参数的数量，但是允许乘法的变化。在本节中，我
们将探索 CNN 的架构，与 cnn-trad-fpool3 不同，我们将模型大小限制为 250 K，但不限制
乘法。
为了提高 CNN 的性能，我们将增加功能地图。如果我们想要增加功能图，但要保持参
数不变，我们必须在时间和频率上探索采样。考虑到我们已经在 cnn-trad-fpool3 中使用了频
率，在本节中我们将探索次采样。
以前，传统的聚在一起已经被用于声学建模[4,8]，但还没有显示出希望。我们的基本原
理是，在声学建模中，子词单元（即我们想要在很短的时间内对其进行分类（例如：10-30ms)。
因此，在时间上共享是有害的。然而，在 KWS 中，关键字单元出现的时间要长得多（例如,50
- 100 ms)。因此，我们将探索是否可以通过跨步或池的方式对信号进行采样，从而改进
cnn-trad-fpool3。应该注意的是，在使用多个卷积子网络[5,9]时，及时地池是有帮助的。然
而，这种方法增加了参数的数量，对于我们的 KWS 任务来说，计算开销很大。据我们所知，
这是第一次用较长的声学单元来探索常规的次采样。
3.4.1 时间跨度
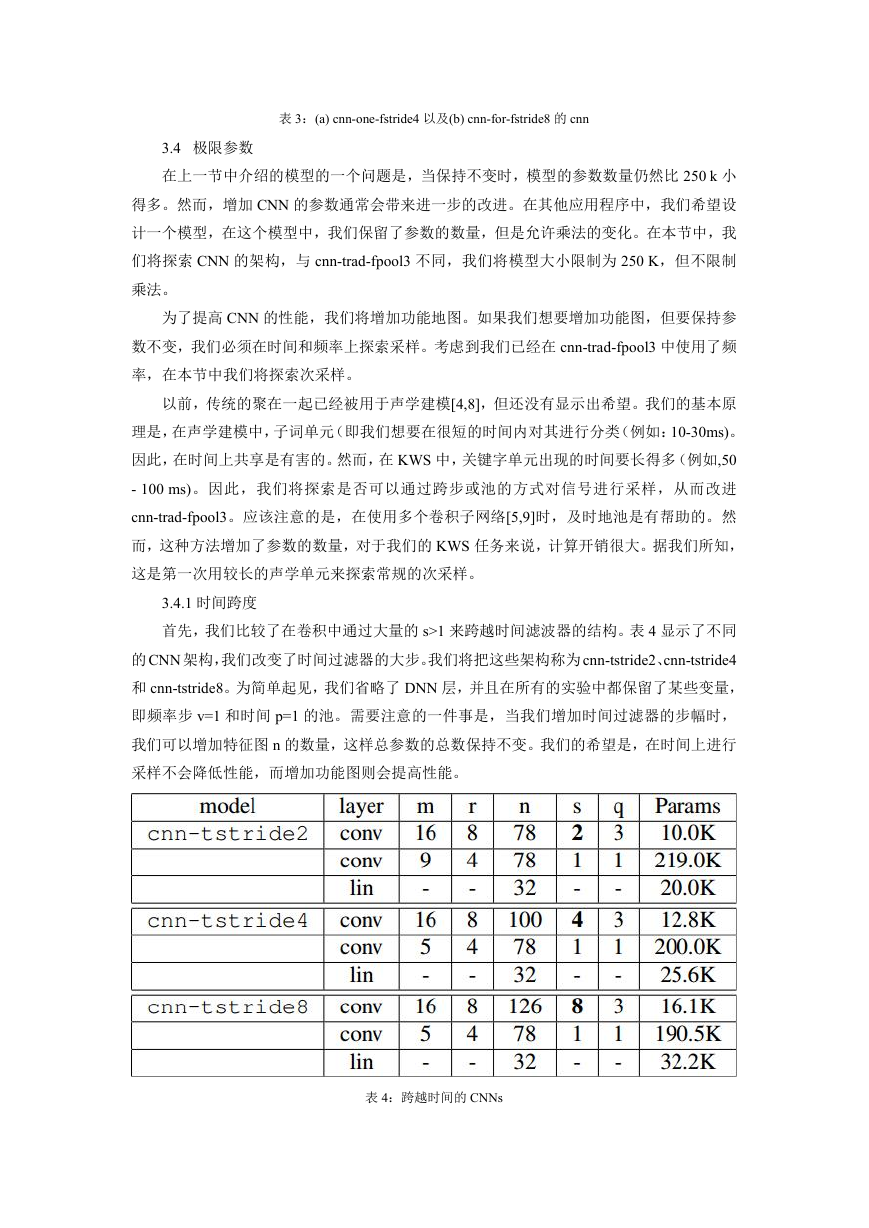
首先，我们比较了在卷积中通过大量的 s>1 来跨越时间滤波器的结构。表 4 显示了不同
的 CNN 架构，我们改变了时间过滤器的大步。我们将把这些架构称为 cnn-tstride2、cnn-tstride4
和 cnn-tstride8。为简单起见，我们省略了 DNN 层，并且在所有的实验中都保留了某些变量，
即频率步 v=1 和时间 p=1 的池。需要注意的一件事是，当我们增加时间过滤器的步幅时，
我们可以增加特征图 n 的数量，这样总参数的总数保持不变。我们的希望是，在时间上进行
采样不会降低性能，而增加功能图则会提高性能。
表 4：跨越时间的 CNNs
3.4.2 池的时间
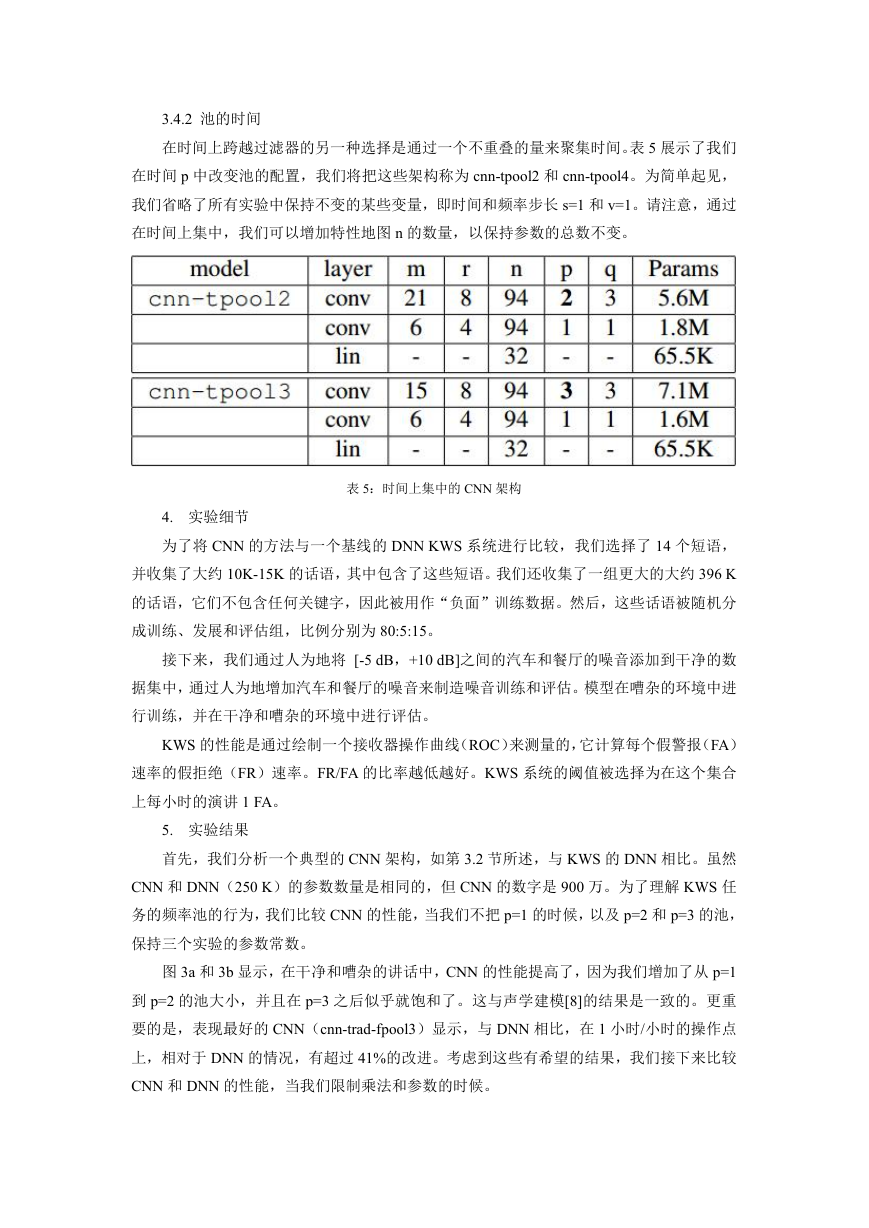
在时间上跨越过滤器的另一种选择是通过一个不重叠的量来聚集时间。表 5 展示了我们
在时间 p 中改变池的配置，我们将把这些架构称为 cnn-tpool2 和 cnn-tpool4。为简单起见，
我们省略了所有实验中保持不变的某些变量，即时间和频率步长 s=1 和 v=1。请注意，通过
在时间上集中，我们可以增加特性地图 n 的数量，以保持参数的总数不变。
表 5：时间上集中的 CNN 架构
4. 实验细节
为了将 CNN 的方法与一个基线的 DNN KWS 系统进行比较，我们选择了 14 个短语，
并收集了大约 10K-15K 的话语，其中包含了这些短语。我们还收集了一组更大的大约 396 K
的话语，它们不包含任何关键字，因此被用作“负面”训练数据。然后，这些话语被随机分
成训练、发展和评估组，比例分别为 80:5:15。
接下来，我们通过人为地将 [-5 dB，+10 dB]之间的汽车和餐厅的噪音添加到干净的数
据集中，通过人为地增加汽车和餐厅的噪音来制造噪音训练和评估。模型在嘈杂的环境中进
行训练，并在干净和嘈杂的环境中进行评估。
KWS 的性能是通过绘制一个接收器操作曲线（ROC）来测量的，它计算每个假警报（FA）
速率的假拒绝（FR）速率。FR/FA 的比率越低越好。KWS 系统的阈值被选择为在这个集合
上每小时的演讲 1 FA。
5. 实验结果
首先，我们分析一个典型的 CNN 架构，如第 3.2 节所述，与 KWS 的 DNN 相比。虽然
CNN 和 DNN（250 K）的参数数量是相同的，但 CNN 的数字是 900 万。为了理解 KWS 任
务的频率池的行为，我们比较 CNN 的性能，当我们不把 p=1 的时候，以及 p=2 和 p=3 的池，
保持三个实验的参数常数。
图 3a 和 3b 显示，在干净和嘈杂的讲话中，CNN 的性能提高了，因为我们增加了从 p=1
到 p=2 的池大小，并且在 p=3 之后似乎就饱和了。这与声学建模[8]的结果是一致的。更重
要的是，表现最好的 CNN（cnn-trad-fpool3）显示，与 DNN 相比，在 1 小时/小时的操作点
上，相对于 DNN 的情况，有超过 41%的改进。考虑到这些有希望的结果，我们接下来比较
CNN 和 DNN 的性能，当我们限制乘法和参数的时候。
在这一节中，我们比较了在第 3 节中描述的各种 CNN 架构，当我们将乘法的数量限制
为 500 k 时。图 4a 和 4b 显示了干净和嘈杂的讲话的结果。性能最好的系统是 cnn-one-fstride4，
在 这 个 系 统 中 ， 我 们 在 频 率 滤 波 器 上 有 50%的 重 叠 ， 但 不 经 常 在 频 率 上 聚 集 。 这 比
cnn-one-fstride8 的性能要好得多，它有一个非重叠的过滤器步。此外，如果对 cnn-1-fpool3
的改进提供了改进，它会在频率上聚集。正如第 5.1 节所演示的那样，在频率上共享是很有
帮助的，因为它的计算开销很大，因此我们必须大幅减少功能图来限制计算。因此，如果我
们处在一个被限制的情况下，首选的 CNN 架构是用重叠的方式来跨越过滤器。
在 1FA/hr 的操作点上，最好的性能系统 cnn-1-fstride4 提供了 27%的相对改进，而在 DNN
上的噪声相对提高了 29%。
在本节中，我们比较了 CNN 的架构，其中我们将乘法的数量与第 5.1 节中表现最好的
系统相匹配，即 cnn-trad-fpool3。图 5a 和 5b 显示了不同架构的性能，当我们在频率上跨卷
积滤波器时，如第 3.4.1 节所述。在时间上跨越过滤器的所有架构都比不跨时间过滤器的
cnn-trad-fpool3 的性能稍差。
与之相比，图 6a 和 6b 在我们将卷积滤波器与时间进行比较时，比较了性能。系统
cnn-tpool2，以 p=2 的时间池，是性能最好的系统。这些结果表明，在次采样前，及时地将
相邻帧之间的关系进行建模，比预先选择相邻帧要过滤的时间更有效。此外，在预测长关键
字单元时，及时地将其与 cnn-trad-fpool3 相比有 6%的相对改进，但在噪声中与 cnn-trad-fpool3
有相似的性能。此外，cnn-tpool2 显示了相对于 DNN 的相对改善 44%，噪音相对提高了 41%。
据我们所知，这是第一次在没有子网络的情况下，在没有子网络的情况下，对语音任务有帮
助。
6. 总结
在本文中，我们探索了基于 CNNs 的 KWS 任务。当我们限制相乘或参数的数量时，我
们将 cnn 与 dnn 进行比较。当限制相乘时，我们发现在频率上移动卷积滤波器在干净和嘈杂
的条件下，在性能上的相对改善超过了 27%。当限制参数时，我们发现在干净和嘈杂的环
境中，在时间上的共享会导致超过 41%的相对改善。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
