logo资料库

求解无线传感器网络定位问题的线性规划算法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.93M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    ISSN 1000 1239 CN 11 TP 46 (5) : 705 - 712 , 2009 1777 计算机研究与发展 Journal of Computer Research and Development 求解无线传感器网络定位问题的线性规划算法 王珊珊1 ,2 　殷建平1 　张国敏1 　蔡志平1 1 (国防科学技术大学计算机学院 　长沙 　410073) 2 (中国人民解放军 66356 部队自动化工作站 　天津 　300182) (diamond_shan @yahoo . com. cn) A Linear Programming Algorithm for Wireless Sensor Net works Localization Wang Shanshan1 ,2 , Yin Jianping1 , Zhang Guo min1 , and Cai Zhiping1 1 ( Colle ge of Com p uter , N ational Uni versit y of De f ense Technolog y , Chan gsha 410073) 2 ( W orkstation of A utom atiz ation , Unit 66356 , People s L iberation A rm y , Ti anj i n 300182) Abstract 　Wireless sensor networks are widely applied in many fields. Sensor node localization p roblem is t he basis and p rerequisite for mo st applications. A linear p rogramming algorit hm is p resented for wireless sensor networks localization. The received signal st rengt h indications ( RSSI) and empirical radio p ropagatio n model are used to deduce t he relationship s of t he distances between co mmunicable node pairs in a wireless sensor network. And t he communicatio n range is used to estimate t he distances between communicable paired nodes. These estimated distances are modeled as a set of square const raint s by app roximating circle to square. And a linear p rogramming p roblem for t hese const raint s is employed to substit ute t he p rogramming p roblem wit h quadric const raint s. A global solution of t he linear p rogramming p roblem yields estimations for t he unknown node po sitions. Then t he node ordinatet s are obtained. Simulatio n result s show t hat p referable localization accuracy can be achieved when anchors are dist ributed near t he f ringe of t he networks. Some analyses are made to validate t he influences of anchor dist ribution , t he number of anchors , and t he connectivity on t he localization error. Furt hermore , compared wit h t he convex po sition estimation for sensor node localization , t he linear p rogramming localization algorit hm enormously declines t he times for solving p rogramming p ro blems , and has smaller localization error when wit h t he same simulation conditions. Key words 　wireless sensor networks ; localizatio n ; linear p rogramming ; RSSI ; anchor nodes 摘 　要 　传感器节点的定位问题是无线传感器网络中的基础性问题之一. 提出了一种线性规划算法用于 求解无线传感器网络定位问题. 该算法利用 RSSI 值和经验的无线信号传播模型推导出所有可通信节 点间距离的相对关系 ,利用节点的通信半径估算出可通信节点间的距离 ,并以此为约束条件利用矩形近 似圆形 ,将二次约束的规划问题转化为线性规划问题 ;求解该线性规划问题便可得未知节点坐标. 通过 仿真实验 ,证明了当锚节点分布在网络边缘时该算法能得到较好的定位效果 ,分析了锚节点分布 、锚节 点个数 、网络连通度等实验参数对定位结果的影响. 相比凸规划定位算法 ,该算法大大降低了求解规划 问题的次数 ,且在相同的实验条件下定位误差更小. 关键词 　无线传感器网络 ;定位 ;线性规划 ; RSSI ;锚节点 中图法分类号 　TP393 　收稿日期 :2007 - 09 - 07 ;修回日期 :2008 - 11 - 25 　基金项目 :国家自然科学基金项目 (60603062 ,60373023) ; 国家“九七三”重点基础研究发展计划基金项目 (2007CB310901) ; 湖南省自然科 学基金项目 (06JJ 3035)
    2 < 607 计算机研究与发展 　2009 , 46 (5) 　　无线传感器网络 ( wireless sensor networks , WSN) 是一种具有感知能力 、计算能力和无线通信 能力的全新的信息处理平台 ,被广泛应用于国防军 事 、环境监测 、交通管理 、医疗卫生等诸多领域 ,实现 复杂的大范围监测和追踪任务. 由于某些情况下传 感器节点部署时的不可控制性 (例如通过飞机抛 撒) ,网络中大多数节点的位置不能事先确定 ,而对 大多数应用来说 ,只有结合了节点的位置信息传感 器获取的数据才有实际意义. 此外 ,节点的自身定位 还可以应用于 WSN 协议的研究 ,例如设计基于节 点位置信息的路由算法以提高路由效率等. 因此 ,节 点自身定位已成为无线传感器网络中一个重要的研 究方向. 本文提出一种求解无线传感器网络定位问题的 线性规划算法. 收集网络中所有节点间的 RSSI 值 , 利用经验的无线信号传播模型 ,推导出所有可通信 节点间距离的相对关系 ,并给出距离的估算方法 ,然 后以这些距离为约束条件 ,用线性规划的方法求解 出节点的位置信息. 本算法对于二维的各向同性的 WSN ,将节点的圆形通信区域近似为矩形 ,可将二 次的约束条件转化为线性的 ,从而用线性规划的方 法求解 ,降低了计算复杂性. 另外 ,本算法消除了路径长度和路径损耗之间 的比例因子对距离估算的影响 ,使算法可以在各种 不同的环境中适用 ,甚至可以利用距离估算的结果 推导出这个与环境相关的比例因子 ,从而实现对未 知环境的认知. 1 　相关研究工作 根据定位过程中是否测量实际节点间的距离 , based) 定 把定位算法分为两类 :基于测距的 ( range f ree) 定位算法. range 位算法和无需测距的 ( range based 定位算法需要测量节点间的绝对距离或角度 信息 ,使用三边测量 、三角测量或极大似然估计定位 法计算节点位置. 这类方法在获得较高的定位精度 的同时 ,也需要额外的硬件支持 ,而且测距技术本身 也存在着测距误差 ,需要多次测量和循环求精的方 法进行精化 ,会产生大量计算和通信开销 ,因此不适 用于低功耗 、低成本的应用领域. range f ree 定位算 法无需测量节点间的绝对距离和角度信息 ,而是利 用网络连通性等信息计算节点的位置. 这类算法不 需要额外的硬件支持 ,通信开销小 ,更适用于 WSN . 虽然获得的定位精度较低 ,但是对于 WSN 大多数 应用 ,粗精度定位已经足够 ,文献[ 1 ]指出 ,当定位误 差小于传感器节点无线通信半径的 40 %时 ,定位误 差对路由性能和目标追踪精确度的影响不会很大. 因此 ,range f ree 定位算法已经越来越受到研究者 的关注. 典型的 range f ree 定位算法如质心算法[ 2 ] 、凸 规划定位算法[ 3 ] 、DV Hop 算法[ 4 ] 只利用了节点间 的连通信息. 而文献[ 1 ]提出的 A PIT 算法除利用连 通信息外 ,还利用了节点接收到的邻居节点发送的 无线信号强度值 RSSI 来判断节点间的相对距离. RSSI 值是与距离相关的信息 ,它可以由传感器节点 自身测量得到 ,不需要额外的硬件支持. 与单纯利用 连通信息的算法相比 ,RSSI 增添了额外的有价值的 信息 ,因此 ,必然会提高定位的精度. 利用网络的连 通信息 和 RSSI 两 者 共 同 完 成 定 位 似 乎 已 经 为 WSN 节点自身定位的研究开辟了一条新的思路 , 有许 多 新 颖 的 算 法 相 继 产 生 , 例 如 ROCRSSI[5 ] , RSSQ[6 ] 和 SRangeQ[ 7 ] 等. 虽然在室内环境下 RSSI 方 法的性能较弱 ,但是在室外条件下 ,在粗粒度定位允 许的范围内 ,RSSI 依然是一种廉价有效的解决方案. 目前的算法中已有一些采用规划的方法进行定 位 ,如凸规划定位算法[ 3 ] 、半定规划定位算法[ 8 ] . 凸 规划定位算法将节点间点到点的通信连接视为节点 位置的几何约束 ,将节点定位问题转化为凸约束优 化问题 ,但是该算法的缺点在于计算每个未知节点 的坐标都要求解 4 次规划 ,求解规划的次数与网络 的规模成正比 ,因此计算量过大. 半定规划定位算法 除了将节点间的通信连接作为约束条件外 ,还增加 了两点间的距离大于等于某个下限值的约束 ,使得 定位的结果更加精确 ,但是由于约束条件的增加也 造成了较大的计算量. 2 　RSSI LP 定位算法 2. 1 　算法模型 将 WSN 看做一个无向图 G = (V , E) ,V 为网络 中传感器节点的集合 , E 为相连接的节点组成的边 的集合. G 中共有 n 个节点 ,其中 m 个锚节点 (位置 已知的节点) ,若点 u , v ∈V 间可以通信 , 则存在一 条边 e( u , v) ∈E. 对每一条边 e( u , v) ∈E 都有一个 相关联的值 c( u , v) ∈C ,在本算法中 c 为节点间的 RSSI 值. 设 A V 为锚节点的集合 , 那么定位问题 就可以描述为求解每个未知节点 u ∈V \ A 的坐标 值 ( x , y) 的问题.
    王珊珊等 :求解无线传感器网络定位问题的线性规划算法 707 若 G 中存在边 e ( u , v) ∈E ,则说明节点 u , v 之 间可以通信 ,设 u , v 间的距离为 d ( u , v) ,我们利用 c( u , v) 与 d ( u , v) 之间的关系 ,找到所有的边与边 之间的距离相对关系 , 由此估算可通信节点间的距 离 ,进而用线性规划算法进行定位. 2. 2 　利用 RSSI 值估算距离 设 Pi j 为由节点 j 发送信号到节点 i 后节点 i 所 Δ0 ) , 测得的接收能量. Pi j 可以表示为[9 ] Pi j = Π0 - 10 np log10 ( di j (1) 其中 , Pi j 的单位为 dBm , di j 为 i , j 两点间的实际距 离 ,Π0 ( dBm) 为相对于参考距离 Δ0 的接收能量 , 典 型的取Δ0 = 1m ,Π0 由自由空间路径损耗公式计算 得到[9 ] , np是一个与环境相关的路径损耗指数 ,典型 的取 2～4. 这个 Pi j 对应图 G 中的一条边 e ( i , j) ,再 考虑另一条边 e( k , l) ,则有 : Pkl = Π0 - 10 np log10 ( dkl Δ0 ) . 　　联立式 (1) (2) ,取Δ0 = 1m ,得到 : Π0 - Pi j Π0 - Pkl = log10 di j log10 dkl , (2) (3) 于是 ,就可以得到 e( i , 关系 ,如式 (4) : j) 和 e( k , l) 两条边的距离的 di j = dkl (4) 其中 , Pi j , Pkl 为测量得到 ,Π0 为已知量 ,这样就找到 了每段距离与距离之间的可计算关系. Pi j - Π0 Pkl - Π0 , 在理想情况下 ,两点间的距离越长所接收到的信 号强度就越小 ,那么最小的接收信号强度所对应的两 点间的距离就是最长的. 当收集到整个网络全部的 RSSI 值后 ,在 RSSI 值的集合 C 中找到最小值 : c ( i , j) , cmin = Pmin = min e( i , j) ∈E (5) 那么 Pmin 所对应的两点间距离就是最长的 , 记为 dmax . 于是根据式 (4) , 便可以得到 G 中任意一条边 e ( i , j) 所对应的两点间距离 di j ,表示为 Pi j - Π0 Pmin - Π0 . di j = dmax (6) 　　因为 dmax 为网络中可通信节点间距离的最大 值 ,当两节点间距离大到一定程度时 ,两节点将不再 能通信 , dmax也更加趋近于传感器节点的通信半径 R ,因此 ,在算法中近似地取 dmax = R , 代入式 ( 6) 中 即可得边 e( i , j) 的估计距离 : Pi j - Π0 Pmin - Π0 . dij ES T = R (7) 　　通过式 (7) 便可以求得图中所有边的估计距离. 需要指出的是 ,虽然近似地取 dmax = R , 但实际情况 下 R ≥dmax , 因此得到的可通信节点间的估计距离 应大于等于两点间的实际距离 ,即 dij ES T ≥di j , 这样 的近似会给算法带来一定的误差. 另外 ,算法通过式 (4) 在找到节点间距离相对关 系的同时 ,消除了式 (1) 中的 np . np 是无线信号传播 模型中路径长度和路径损耗之间的比例因子 , 在不 同的环境下 np的取值不同. 消除了这个因子之后带 来的好处是使得观察者在不知道 np 值的情况下也 可以估算节点间的距离 ,因此 ,该算法可适用于各种 不同的环境 ,成为一个普遍意义上的距离估算方法. 而且 ,通过该算法我们甚至可以反过来推导出估算 np的公式 : np = Π0 - Pi j 10 log10 di j = Π0 - Pmin 10 log10 R , (8) 其中 , R 为传感器节点的通信半径. 当传感器抛洒在 未知环境中时 ,这个结果也可以作为对未知环境观 测的一个角度. 2. 3 　线性规划定位算法 设节点 i , j 的坐标分别为 ( x i , y i ) ( x j , y j ) , 则 两点间的距离 di j 为 di j = ( x i - x j ) 2 + ( y i - y j ) 2 . (9) 　　设向量 x = [ x1 y1 … x m y m x m + 1 y m + 1 … x n y n ] T ,前 2 m 项为已知的锚节点的坐标 , 后 2 n - 2 m 项为未知节点的坐标. 由于第 2. 2 节中估算得到的 可通信两点间距离 dij ES T ≥di j , 因此用 dij ES T 代替式 (9) 中的 di j 后可得 : ( x i - x j ) 2 + ( y i - y j ) 2 ≤ dij ES T . (10) 　　假设传感器节点在感知区域内随机均匀分布 , 锚节点是人工均匀部署的 ,那么理想情况下 ,所有节 点的质心与所有锚节点的质心应该是重合的. 因此 , 我们以所有传感器节点的质心和所有锚节点的质心 之间距离向量的范数作为目标函数 , 以式 (10) 表示 的可通信节点间距离为约束条件 , 可将未知节点的 定位问题描述为二次约束的规划问题 : min ‖xn - xm ‖2 s. t . ( x i - x j ) 2 + ( y i - y j ) 2 ≤ d2 　1 ≤i , j ≤ n 且 e ( i , j) ∈ E , x i = x iA nchor , ij ES T , 1 ≤i ≤ m , y i = y iA nchor , 其中 , xn = ∑ xi n i = 1 n n ∑ yi i = 1 n , , xm = ∑ xi m i = 1 m m ∑ yi i = 1 m , , xn 为所有传感器节点的质心 , xm 为所有锚节点的质 心. 对于该二次约束的规划问题 ,可以将其转化为二 次锥规划进行求解. 虽然求解二次锥规划问题有多 项式时间内的算法 ,但仍然具有一定的计算量.
    807 计算机研究与发展 　2009 , 46 (5) 别以 x , - x , y , - y 作为目标函数求解四次规划问 题 ,这样进行一次定位共需要进行 4 ( n - m) 次规划 问题的求解 , m 为锚节点个数 , n - m 为未知节点的 个数. 而本文的算法找到了一个合理有效的目标函 数 ,只需要进行一次线性规划问题的求解就可以实 现全部节点的定位 , 大大降低了计算量. 如表 1 所 示. 也就是说 ,在相同的条件下 , 如果用同样的方法 求解规划问题 ,凸规划定位算法所需的时间和计算 量是线性规划定位算法的 4 ( n - m) 倍. Table 1 　Comparison of Solving Times for Convex Position Estimation and Linear Programming Localization Algorithm 表 1 　线性规划定位算法与凸规划定位算法求解规划问题 的次数 Localization Algorit hm Convex Position L P Localization Estimation Algorit hm Times of Solving Programming 4 ( n - m) 1 3 　实验结果 实验在 Matlab7.0 的环境下进行 ,采用 Matlab Optimization Toolbox 求解上述线性规划问题. 设 传感器节点的通信半径 R = 10 ,实验首先在 5 R ×5 R 的感知区域内均匀分布 100 个传感器节点 ,图 2 表 示为由节点间的连通信息获得的传感器节点的连接 图. 节点间的 RSSI 值使用经验的无线信号传播模 型进行模拟[ 9 ] : Pi j = Π0 - 10 np log10 ( di j Δ0 ) + Xσ. 　　在公式中加入 Xσ表示均值为 0 、方差为σ的高 斯随机变量. 在实际环境中 ,无线信道受环境影响存 在反射 、多径传播 、背景干扰等问题 , 会产生不同的 传播损耗 ,为模拟真实性引入高斯噪声 Xσ. 在本实 验中 ,取 Π0 = - 30dBm ,Δ0 = 1m , np = 3 ,σ= 2. Fig. 2 　Connection graph of sensor nodes. 图 2 　传感器节点间的连接图 Fig. 1 　Approximating the circle connection area to it s circumsquare. 图 1 　用圆的外接矩形近似传感器节点的圆形连通区域 在各向同性的 WSN 中 ,若节点 i , j 间的距离有 约束 ( x i - x j ) 2 + ( y i - y j ) 2 ≤d2 ij ES T ,那么节点 j 就在 以节点 i 为圆心 d ij ES T 为半径的圆形区域内 , 如图 1 中圆形区域部分所示. 我们用这个圆形区域的外接 矩形来近似这个圆形区域 , 这时两节点间的距离约 束就 可 以 表 示 为 x i - x j ≤dij ES T 和 y i - y j ≤ dij ES T ,于是 ,上述具有二次约束的规划问题就可以 近似为 min ∑ x i n i = 1 n m ∑ x i i = 1 m - n + ∑ y i i = 1 n m ∑ y i i = 1 m - , s. t . | x i - x j | ≤ dij ES T , | y i - y j | ≤ dij ES T , 　1 ≤i , j ≤ n 且 e ( i , j) ∈ E , x i = x iA nchor , 1 ≤i ≤ m , y i = y iA nchor , 这样就把二次约束的规划问题转化成了线性规划问 题. 求解二次锥规划问题的计算复杂性优于 O ( k3 ) , 而求解线性规划问题的计算复杂性优于 O ( k2 ) , k 网络中可连通的边数. 因此 , 转化为线性规划 , 降低 了计算复杂性 ,减小了计算量. 但同时 , 这样的转化 也给定位带来了一定的误差 ,如图 1 所示 ,本该属于 圆形区域内的节点通过线性规划模型求解后的坐标 有可能落在图中的阴影部分的区域内. 在精度允许 的范围内 ,由于更小的计算量 ,本算法更加使用于低 功耗的无线传感器网络. 但由于本文算法为集中式 定位算法 ,在前期收集约束条件的过程中会带来一 定的时间和能量开销 ,因此 ,本算法并不适用于高密 度部署的传感器网络. 在高密度部署的网络中可以 采取分层或分簇的方式先将网络进行划分 , 然后在 子网中利用线性规划定位算法进行定位. 现有的一种集中式定位算法凸规划定位算法[3 ] 同样以网络中的可通信节点间的距离范围作为约束 条件 ,但该算法对每一个未知节点 x ( x , y) ,需要分
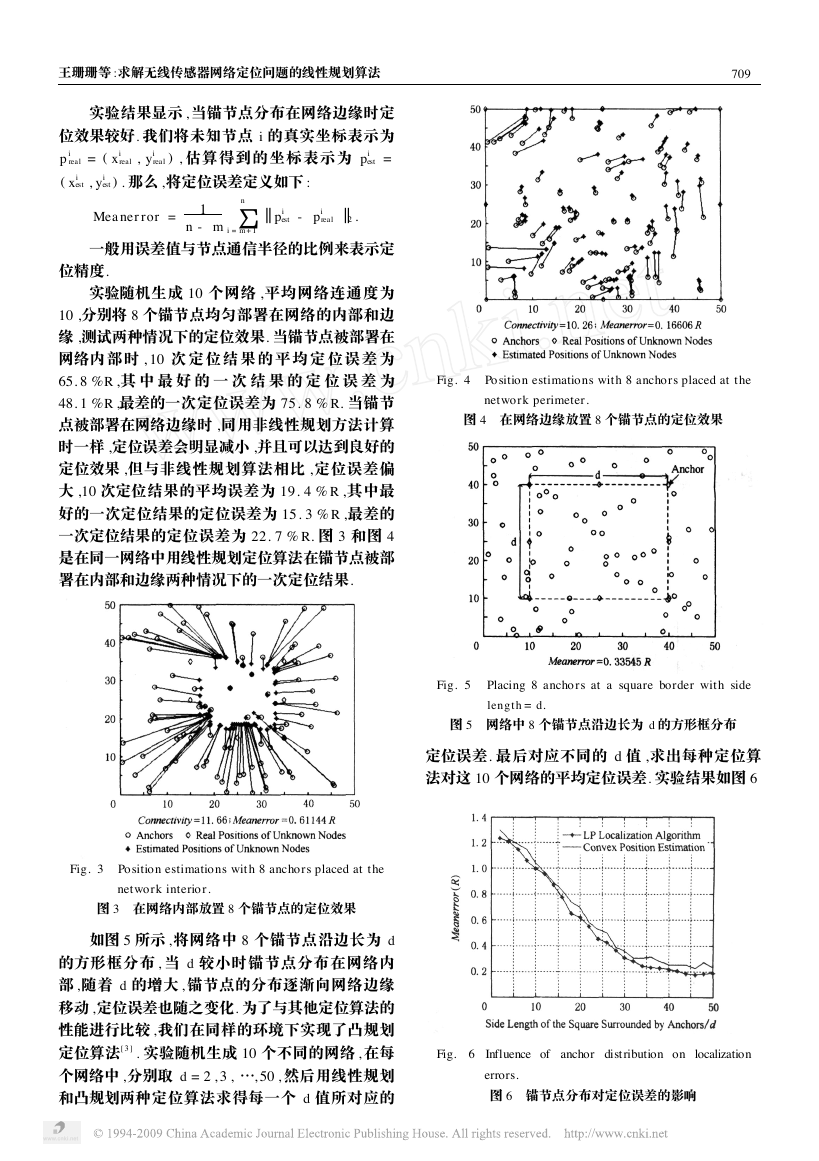
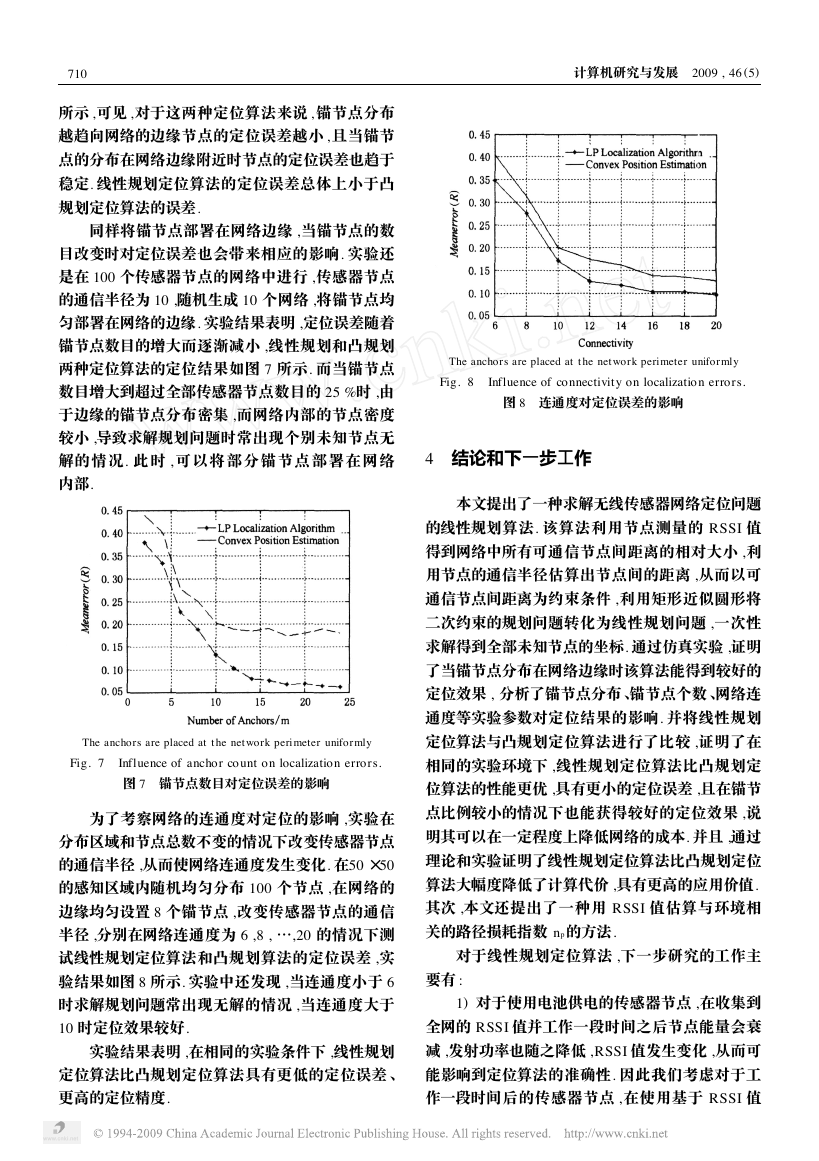
    王珊珊等 :求解无线传感器网络定位问题的线性规划算法 907 实验结果显示 , 当锚节点分布在网络边缘时定 位效果较好. 我们将未知节点 i 的真实坐标表示为 real = ( x i p i est = ( x i est , y i real ) , 估算得到的坐标表示为 pi est ) . 那么 ,将定位误差定义如下 : real , y i Meanerror = n 1 n - m ∑ i = m +1 ‖pi est - pi real ‖2 . 　　一般用误差值与节点通信半径的比例来表示定 位精度. 实验随机生成 10 个网络 ,平均网络连通度为 10 ,分别将 8 个锚节点均匀部署在网络的内部和边 缘 ,测试两种情况下的定位效果. 当锚节点被部署在 网络内 部 时 , 10 次 定 位 结 果 的 平 均 定 位 误 差 为 65. 8 %R ,其 中 最 好 的 一 次 结 果 的 定 位 误 差 为 48. 1 %R ,最差的一次定位误差为 75. 8 % R. 当锚节 点被部署在网络边缘时 ,同用非线性规划方法计算 时一样 ,定位误差会明显减小 ,并且可以达到良好的 定位效果 ,但与非线性规划算法相比 ,定位误差偏 大 ,10 次定位结果的平均误差为 19. 4 % R ,其中最 好的一次定位结果的定位误差为 15. 3 % R ,最差的 一次定位结果的定位误差为 22. 7 % R. 图 3 和图 4 是在同一网络中用线性规划定位算法在锚节点被部 署在内部和边缘两种情况下的一次定位结果. Fig. 4 　Po sition estimations with 8 anchors placed at the network perimeter. 图 4 　在网络边缘放置 8 个锚节点的定位效果 Fig. 5 　Placing 8 anchors at a square border with side lengt h = d. 图 5 　网络中 8 个锚节点沿边长为 d 的方形框分布 定位误差. 最后对应不同的 d 值 ,求出每种定位算 法对这 10 个网络的平均定位误差. 实验结果如图 6 Fig. 3 　Position estimations with 8 anchors placed at the network interior. 图 3 　在网络内部放置 8 个锚节点的定位效果 如图 5 所示 ,将网络中 8 个锚节点沿边长为 d 的方形框分布 , 当 d 较小时锚节点分布在网络内 部 ,随着 d 的增大 , 锚节点的分布逐渐向网络边缘 移动 ,定位误差也随之变化. 为了与其他定位算法的 性能进行比较 ,我们在同样的环境下实现了凸规划 定位算法[3 ] . 实验随机生成 10 个不同的网络 , 在每 个网络中 ,分别取 d = 2 , 3 , …, 50 , 然后用线性规划 和凸规划两种定位算法求得每一个 d 值所对应的 Fig. 6 Influence of anchor distribution on localization errors. 图 6 　锚节点分布对定位误差的影响
    017 计算机研究与发展 　2009 , 46 (5) 所示 ,可见 ,对于这两种定位算法来说 , 锚节点分布 越趋向网络的边缘节点的定位误差越小 , 且当锚节 点的分布在网络边缘附近时节点的定位误差也趋于 稳定. 线性规划定位算法的定位误差总体上小于凸 规划定位算法的误差. 同样将锚节点部署在网络边缘 ,当锚节点的数 目改变时对定位误差也会带来相应的影响. 实验还 是在 100 个传感器节点的网络中进行 ,传感器节点 的通信半径为 10 ,随机生成 10 个网络 ,将锚节点均 匀部署在网络的边缘. 实验结果表明 ,定位误差随着 锚节点数目的增大而逐渐减小 ,线性规划和凸规划 两种定位算法的定位结果如图 7 所示. 而当锚节点 数目增大到超过全部传感器节点数目的 25 %时 ,由 于边缘的锚节点分布密集 ,而网络内部的节点密度 较小 ,导致求解规划问题时常出现个别未知节点无 解的情况. 此 时 , 可 以将 部分 锚节点 部署 在网 络 内部. The anchors are placed at t he network perimeter uniformly Fig. 7 　Influence of anchor count on localization errors. 图 7 　锚节点数目对定位误差的影响 为了考察网络的连通度对定位的影响 ,实验在 分布区域和节点总数不变的情况下改变传感器节点 的通信半径 ,从而使网络连通度发生变化. 在50 ×50 的感知区域内随机均匀分布 100 个节点 ,在网络的 边缘均匀设置 8 个锚节点 ,改变传感器节点的通信 半径 ,分别在网络连通度为 6 ,8 , …,20 的情况下测 试线性规划定位算法和凸规划算法的定位误差 ,实 验结果如图 8 所示. 实验中还发现 ,当连通度小于 6 时求解规划问题常出现无解的情况 ,当连通度大于 10 时定位效果较好. 实验结果表明 ,在相同的实验条件下 ,线性规划 定位算法比凸规划定位算法具有更低的定位误差 、 更高的定位精度. The anchors are placed at t he network perimeter uniformly Fig. 8 　Influence of connectivity on localization errors. 图 8 　连通度对定位误差的影响 4 　结论和下一步工作 本文提出了一种求解无线传感器网络定位问题 的线性规划算法. 该算法利用节点测量的 RSSI 值 得到网络中所有可通信节点间距离的相对大小 ,利 用节点的通信半径估算出节点间的距离 ,从而以可 通信节点间距离为约束条件 ,利用矩形近似圆形将 二次约束的规划问题转化为线性规划问题 ,一次性 求解得到全部未知节点的坐标. 通过仿真实验 ,证明 了当锚节点分布在网络边缘时该算法能得到较好的 定位效果 , 分析了锚节点分布 、锚节点个数 、网络连 通度等实验参数对定位结果的影响. 并将线性规划 定位算法与凸规划定位算法进行了比较 ,证明了在 相同的实验环境下 ,线性规划定位算法比凸规划定 位算法的性能更优 ,具有更小的定位误差 ,且在锚节 点比例较小的情况下也能获得较好的定位效果 ,说 明其可以在一定程度上降低网络的成本. 并且 ,通过 理论和实验证明了线性规划定位算法比凸规划定位 算法大幅度降低了计算代价 ,具有更高的应用价值. 其次 ,本文还提出了一种用 RSSI 值估算与环境相 关的路径损耗指数 np的方法. 对于线性规划定位算法 ,下一步研究的工作主 要有 : 1) 对于使用电池供电的传感器节点 ,在收集到 全网的 RSSI 值并工作一段时间之后节点能量会衰 减 ,发射功率也随之降低 ,RSSI 值发生变化 ,从而可 能影响到定位算法的准确性. 因此我们考虑对于工 作一段时间后的传感器节点 ,在使用基于 RSSI 值
    ΠΠ ΠΠ 2 王珊珊等 :求解无线传感器网络定位问题的线性规划算法 117 [ 8 ] Biswas P , Ye Y Y. Semidefinite programming for Ad Hoc wireless sensor network localization [ C] Proc of t he 3rd Int Conf on Information Processing in Sensor Networks ( IPSN 04) . New York : ACM , 2004 : 46 - 54 [ 9 ] Rappaport T. Wireless Communications : Principles and Practice [ M ] . Englewood Cliff s , NJ : Prentice Hall , 2002 Wang Shanshan , born in 1982. M. S. candidate in the School of Computer Science at the National University of Defense Technology. Her main research interest is wireless sensor network localization. 王珊珊 ,1982 年生 ,硕士研究生 ,主要研究方向为无线传感 器网络定位算法. Yin Jianping , born in 1963. He received his M. S. degree and Ph. D. degree in computer science f rom the National University of Defense Technology in 1986 and 1990 , respectively. He is p rofessor 的线性规划定位算法时 ,可以根据使用时间的长短 在约束条件中加入权值 ,对可通信节点间距离进行 校正 ,从而提高定位算法的准确性. 2) 对于超大规模或高密度部署的网络 ,用规划 方法进行集中式的定位 ,收集约束条件的过程会产 生很高的计算量. 因此 ,我们考虑将集中式的算法改 进为分布式的算法 ,例如用分层或分簇的方法来实 现在子网内进行局部的集中式定位 ,最终实现整个 网络的定位. 参 考 文 献 [ 1 ] He T , Huang C D , Blum B M. Range f ree localization schemes in large scale sensor networks [ C] Proc of t he 9t h Annual Int Conf on Mobile Computing and Network ( MobiCom 03) . New York : ACM , 2003 : 81 - 95 [ 2 ] Bulusu N , Heidemann J , Est rin D. GPS less low cost outdoor localization for very small devices [J ] . IEEE Personal Communications , 2000 , 7 (5) : 28 - 34 [ 3 ] Dohert y L , Pister K S , Ghaoui L E. Convex position estimation in wireless sensor networks [ C] Proc of t he and Ph. D. supervisor in the School of Comp uter Science at IEEE IN FOCOM 2001. Anchorage : IEEE Computer and the National University of Defense Technology. His main Communications Societies , 2001 : 1655 - 1663 [ 4 ] Nicolescu D , Nat h B. Ad Hoc positioning systems ( APS) [ C] Proc of t he 2001 IEEE Global Telecommunications Conf . San Antonio : IEEE Communications Society , 2001 : research interest s involve artificial intelligence , pattern recognition , algorithm design , and information security. 殷建平 ,1963 年生 ,教授 ,博士生导师 ,主要研究方向为人工 智能 、模式识别 、算法设计 、信息安全等. 2926 - 2931 [ 5 ] Liu C , Wu K , He T. Sensor localization wit h ring overlapping based on comparison of received signal st rengt h indicator [ C] Proc of t he 1st IEEE Int Conf on Mobile Ad hoc and Sensor Systems ( MASS 04 ) . Los Alamitos , CA : IEEE Computer Society , 2004 : 516 - 518 [ 6 ] Patwari N , Hero A. Using proximity and quantized RSS for sensor localization in wireless net works [ C] Proc of t he 2nd ACM Int Workshop on Wireless Sensor Networks and Applications. New York : ACM , 2003 : 20 - 29 [ 7 ] Li X , Shi H C , Shang Y. A sorted RSSI quantization based algorit hm for sensor network localization [ C] Proc of t he 11t h Int Conf on Parallel and Dist ributed Systems. Los Alamitos , CA : IEEE Computer Society. 2005 : 557 - 563 Zhang Guomin , born in 1980. Ph. D. candidate in the School of Computer Science at the National University of Defense Technology. His main research interest is image p rocessing. 张国敏 ,1980 年生 ,博士研究生 ,主要研究方向为图像处理. Cai Zhiping , born in 1975. Ph. D. . His main research interest s include computational complexity , app roximation algorithms and network measurement . 蔡志平 ,1975 年生 ,博士 ,主要研究方向为 计算复杂性 、近似算法 、信息安全. Research Background Wireless sensor networks have been applied in a wide variety of applications. Sensor node localization is the basis and prerequisite for mo st applications. In recent years , many academies and industries have been making an in depth research on sensor node localization technologies. In this paper , a linear programming algorithm is presented for wireless sensor networks localization. The received signal strength indications ( RSSI) and empirical radio propagation model are used to deduce the
    ΠΠ Π ΠΠ 2 2 Π 2 2 217 计算机研究与发展 　2009 , 46 (5) relationship s of the distances between communicable node pairs. And the communication range is used to estimate the distances between communicable paired nodes. These estimated distances are modeled as a set of square constraint s by app roximating circle to square. And a linear programming problem for these constraint s is employed to substitute the p rogramming problem with quadric constraint s. A global solution of the linear p rogramming problem yields estimations for the unknown node positions. Our work is supported by the National Natural Science Foundation of China ( Nos. 60603062 , 60373023) , the Natural Science Foundation of Hunan Province (No . 06JJ 30035) and the National 973 Basic Research Program of China (No . 2007CB310901) . 研发动态 Wi Fi 联盟制定新一代设备间通信标准 WL AN 业界团体美国 Wi Fi 联盟日前宣布 ,目前正在制定无线 L AN 用于设备连接的标准. 除了电视及数码相机等数字 家电设备之外 ,还设想用于产业设备. Wi Fi 联盟的相关人士表示 ,设想用于数码相机向电视等传送拍摄的照片时 ,无需用户 操作便可自动无线传送的用途等. 希望现有的硬件可以采用这一新标准 ,为此该联盟以无需软件升级便可实现新一代标准为 目标 (摘自 :http : www. cnw. com. cn 09 ,网界网) . ,2009 04 微软报告称全球邮件的 97 %是垃圾邮件 据报道 ,日前微软公司的一份一年两次发布的计算机安全报告指出 ,去年下半年 ,全球电子邮件流量中 97. 3 %是垃圾邮 件. 根据微软同一份报告 ,去年上半年 ,垃圾邮件占据了邮件流量的 98. 4 %. 微软这份报告长达 184 页 ,描述了网络和计算机 领域到去年年底的安全状况. 在垃圾邮件的内容上 ,药物和其他产品广告占据了 72 % ,只有一成的垃圾邮件和性功能药物有 关 ,和过去相比有明显的下降. 其他内容包括金融诈骗 、假学历 、约会邀请 ,还有一些是纯图片的垃圾邮件. 面对垃圾邮件肆 虐 ,各路厂商也在加强邮件过滤能力. 比如微软的 Exchange 系统 ,现在每 40 封邮件中就要过滤掉 39 封. Gmail , Hotmail 等免 费邮箱提供商也具备过滤能力 (摘自 :http : 09 ,搜狐 IT) . it . sohu. com ,2009 04 微软被判侵犯专利将赔偿 3. 88 亿美元 据报道 ,美国一家法庭判决微软侵犯了其他公司有关反盗版技术上的专利 ,这是罕见的小公司扳倒微软的案例. 原告是 位于加州的 Uniloc 美国公司和 Uniloc 新加坡公司. 法庭判决认为 ,微软侵权成立 ,必须赔偿原告 3. 88 亿美元. Uniloc 公司主 要研发用于软件和视频游戏的反盗版工具和组件. 该公司表示 ,微软在 Windows 和 Office 软件中的产品激活功能侵犯了他们 的专利. 在产品激活过程中 ,用户首先需要注册成为合法正式用户 ,这一功能的目的是阻止一个软件许可证用于多台电脑. 原 告称 ,他们在 1992 年就获得了专利权. 2003 年 ,该公司就起诉了微软公司 ,最初的判决有利于微软 ,去年联邦上诉法庭推翻了 最初判决 ,要求罗德岛州普罗维德斯地区的法庭重审此案. 最终结论有利于原告 (摘自 : http : 09 ,搜狐 IT) . it. sohu. com ,2009 04 贝瑞特任期最后一次访华 日前 ,英特尔董事长贝瑞特在北京举办的英特尔信息技术峰会 ( IDF2009) 上呼吁 ,应通过技术革新应对全球经济危机. 他 还指出 ,摩尔定律将在未来 15 年内继续有效 ,英特尔不断创新的理念未来也不会改变. 根据公开信息显示 ,贝瑞特将于今年 5 月卸任英特尔公司董事长职务 ,退出该公司的管理事务. 此次在北京举办的 IDF 可能是贝瑞特最后一次以董事长身份访华. 贝瑞特还指出 ,摩尔定律将在未来 15 年内继续发挥作用. 谈及经济危机对全球的影响 ,贝瑞特表示自己也非常关注 ,全球各界 应该通过技术革新应对经济放缓与危机 (摘自 :http : tech. sina. com. cn 08 ,新浪科技) . ,2009 04 国产超百万亿次计算机命名魔方 中国首款超百万亿次超级计算机曙光 5000A 有了名字 ———“魔方”. 日前 ,曙光公司透露 ,将于今年 5 月落户上海超级计 算中心的“魔方”,除了拥有超强计算能力外 ,还拥有全自主 、超高密度 、超高性价比 、超低功耗以及超广泛应用等特点. 2008 年 9 月 16 日 ,曙光 5000A 在曙光天津产业基地正式下线 ,这标志着中国成为继美国后世界上第二个自主设计并制造百万亿次高 性能计算机的国家 (摘自 :http : paper. people. com. cn 07 ,京华时报) . jhsb ,2009 04
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料