Desk Calculator.pdf-资料库

Project 1 Desk Calculator Chapter 1: Introduction This time our task is to write a program that imitates a simple desk calculator .Our calculator can accept an infix expression which includes (, ), +, -, *, /, % and ^(exp exponentiation operator, a^b= a b ). Our program reads test cases from a file “input.txt”. In the file there are several test cases, each occupies one line that contains an infix expression. Proceed until the end of the file. And for each test case, output to a file “output.txt” in one line the value of that expression (accurate up to two decimal places), or an error message “ERROR IN INFIX NOTATION”. Chapter 2: Algorithm Specification Main Frame Begin Try { } End Input (input: string); Infix to Postfix (input: string, output: array of double); Calculate (input: array of double, output: double); Output (output: double);

Infix to Postfix Begin Try { Switch (one char of the string) { Case ‘0’-‘9’or ‘.’: double); Write into output Break; Case operator except ‘)’: Check next until get a char is not in {‘0’-9’,’.’}; String to Double (input: all the chars read, output: Check the stack, if it’s not empty; pop all the operators of the high priority and write into output; Break; Pop and write until meets a ‘(‘ Case ‘)’: Default: throw error; } Pop all the operators left in the stack and write into output; Calculate Begin Try { Switch (one char of the string) { Case operand: Push into stack; Break; Case operator: Calculate and push the result into stack; Break; Default: throw error; } Return the top of the stack (result); } } End Error Processing Caught (Error) Begin End Process (Error);

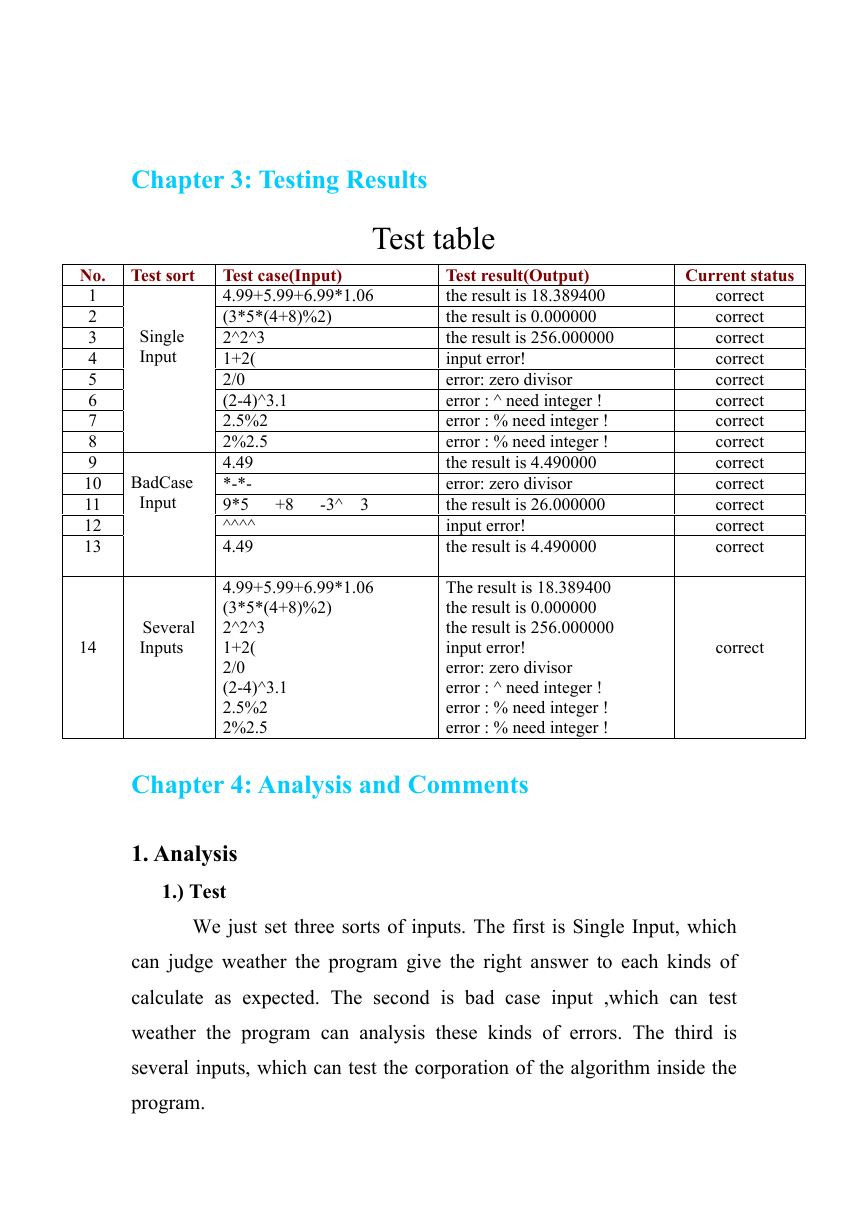
Chapter 3: Testing Results Test table Single Input No. Test sort 1 2 3 4 5 6 7 8 9 10 11 12 13 BadCase Input 14 Several Inputs Test case(Input) 4.99+5.99+6.99*1.06 (3*5*(4+8)%2) 2^2^3 1+2( 2/0 (2-4)^3.1 2.5%2 2%2.5 4.49 *-*- 9*5 +8 -3^ 3 ^^^^ 4.49 4.99+5.99+6.99*1.06 (3*5*(4+8)%2) 2^2^3 1+2( 2/0 (2-4)^3.1 2.5%2 2%2.5 Current status correct correct correct correct correct correct correct correct correct correct correct correct correct correct Test result(Output) the result is 18.389400 the result is 0.000000 the result is 256.000000 input error! error: zero divisor error : ^ need integer ! error : % need integer ! error : % need integer ! the result is 4.490000 error: zero divisor the result is 26.000000 input error! the result is 4.490000 The result is 18.389400 the result is 0.000000 the result is 256.000000 input error! error: zero divisor error : ^ need integer ! error : % need integer ! error : % need integer ! Chapter 4: Analysis and Comments 1. Analysis 1.) Test We just set three sorts of inputs. The first is Single Input, which can judge weather the program give the right answer to each kinds of calculate as expected. The second is bad case input ,which can test weather the program can analysis these kinds of errors. The third is several inputs, which can test the corporation of the algorithm inside the program.

2.)Running time a.) Input (iuput: string) This Algorithm runs in O (N) time. It reads N characters or digitals from “input.txt”. This algorithm only count b times per character or digital into “input.txt”. (b is a constant interger.)This algorithm only count one time per character or digital and a total of bN units. Adding some constant units k that takes time at the beginning and the end of the algorithm, it counts for a total of bN+k units. Above all, the function runs in O (N) time. b.)Calculate (input: array of double, output: double) This Algorithm runs in O (N) time. This algorithm counts b times for each character or digital stored in array by Input (iuput: string) and a tatal of bN units. Adding k units of constant common use, it counts for a total of bN+k units. Above all, the function runs in O (N) time. c.) output (output: string) This Algorithm runs in O (N) time. It outputs N characters or digitals into “output.txt”. This algorithm only count b times per character or digital into “input.txt”. (b is a constant interger.)This algorithm only count one time per character or digital and a total of bN units. Adding some constant units k that takes time at the beginning and the end of the algorithm, it counts for a total of bN+k units. Above all, the function runs in O (N) time. In a word, the total program runs in O (N) time. 2. Comments After some tests and improvement, this program runs well as expected. It gives the proper data that are required in the document. So the program is correct after all. However，there were still some problems . We also have many things to be improved such as the

wrong judge when we type an “enter” at the last line in the “input .txt” .(Fortunately, this bug has been removed from the final program.) And we can add complex number to be calculated to make this project more useful and perfect later. Also , this program can be optimized . If we have more time, I think we can make it much better. From this project, we can have a deep understanding about how to write a file by a c program. Also ,we have seen the importance of a good type of data structure, which can make the program more clearly and can be helpful for debugging and reading. It is quiet important for us to choose the best algorithm in any situation.

----------------------------------------------------------------------------------- Appendix: Source Code (in C) /* Build with Visual C++ */ 1.main.c # include "del.h" void push (double element, double v[]); double pop(double v[]); int sp = 0; double val[MAXVAL]; int main() { char type; double numb; double op2, op3, sum; int i,k; FILE *fpw2; fpw2=fopen("output.txt","w+"); if((k = itop())==-1) /*judge wheter it's an correct return*/ { fprintf(fpw2,"input error!\n"); } do{ /*do-while loop move the calculations to the next line*/ for(i = 0; i

{ fprintf(fpw2,"error: zero divisor\n"); goto tmpend; } break; case '%' : op2 = pop(val); op3 = pop(val); push( ((int)op3 %(int) op2), val); else { fprintf(fpw2,"error : %% need integer !\n"); goto tmpend; } break; case '^' : op2 = pop(val); if(isint(op2) && isint(op3)) op3 = pop(val); if(isint(op2)) { sum = pow(op3,op2); push(sum, val); } else { fprintf(fpw2,"error : ^ need integer !\n"); goto tmpend; } break; } fprintf(fpw2,"the result is %.2f\n",pop(val)); tmpend:; /*if input error or calc error has occured,it jumps here*/ if(!feof(fp)) { goto tmpend; } else break; /*input file ends*/ }while(1); fclose(fp); fclose(fpw2); return 0; } void push(double element, double v[]) { if (sp < MAXVAL) v[sp++] = element; else default : fprintf( fpw2 , "input error!\n"); goto tmpend; } } if((k = itop())==-1) /*and move to the next line*/ { fprintf(fpw2,"input error!\n"); } if(k==0) return 0; /*the input is nothing*/

printf( "error: stack full, can't push %g\n", element); } double pop(double v[]) { if ( sp > 0) return v[--sp]; else { printf( "error: stack empty\n" ); return 0.0; } } 2. ItoP.H # ifndef del_h # define del_h #include #include #include #include # define MAXLEN 100 # define MAXVAL 100 FILE *fp; /*fp point to input.txt*/ int flagfp=1; /*a flag to avoid reopening the input.txt*/ struct Node { int flag; /*1 indicates the type is number,and 2 sign*/ double Number; char Sign; } Data[MAXLEN]; /*to save all datas*/ int isint(double a) /*to judge whether the original input is interger*/ { if(fabs(a-(int)a)<1.0e-5) return 1; return 0; } int itop() /*hanle the input.txt,get its data of line in Data[]*/ { char ch; int i = 0 , t = 0, top = 0; char stack[MAXLEN];/*temporary stack,save signs like + - / and * ^ */ char v[MAXLEN]; /*save the data one by one from input.txt*/ if(flagfp && (fp=fopen("input.txt","r"))==NULL) { goto end; } flagfp=0;/*indicates that input.txt has been opened*/ ch=fgetc(fp); do { if( isdigit(ch) || ch == '.') { /*handle digits*/ do {

资料库

Desk Calculator.pdf

相关推荐

课程资源

热门标签

最新资料