logo资料库

带恢复策略的复杂网络级联失效机理及鲁棒性研究.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：1.73M 资料格式：pdf 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    第 33 卷 第 10 期 2018 年 10月 控 制 与 决 策 and Decision Control Vol.33 No.10 Oct. 2018 文章编号: 1001-0920(2018)10-1841-10 DOI: 10.13195/j.kzyjc.2017.0728 带恢复策略的复杂网络级联失效机理及鲁棒性研究 唐 亮1y, 焦 鹏2, 李纪康2, 靖 可3, 靳志宏1 (1. 大连海事大学 交通运输工程学院，辽宁 大连 116026；2. 沈阳航空航天大学 机电工程学院，沈阳 110136； 3. 大连海事大学 航运经济与管理学院，辽宁 大连 116026) 文献标志码: A 摘 要: 为研究复杂网络在遭遇随机故障或蓄意攻击时的鲁棒性, 考虑节点具有恢复和重复失效等特征, 构建故 障节点概率传播模式下的级联失效模型. 构建节点故障概率随故障次数增加而逐渐降低的故障概率函数, 设计概 率恢复(R) 和阶段恢复(T ) 两种故障节点恢复策略, 并针对ER、WS、NC 和BA 四类网络研究其恢复鲁棒性. 仿真 实验考虑模型中相关参数变化, 揭示其对复杂网络级联失效过程中的鲁棒性影响, 综合分析边鲁棒性和节点鲁棒 性的性能权衡. 仿真结果表明, 在概率恢复策略下, 随着恢复率的增大, 4 类网络级联失效的规模均能够实现有效 降低；而在阶段恢复策略下, 随着参数 T 值增加到不同阈值, 4 类网络鲁棒性指标在级联失效过程中均能够呈现出 突变现象. 关键词: 复杂网络；级联失效；概率恢复策略；阶段恢复策略；鲁棒性；重复失效 中图分类号: N94 Cascading failure mechanism and robustness of complex networks with recovery strategy TANG Liang1y, JIAO Peng2, LI Ji-kang2, JING Ke3, JIN Zhi-hong1 (1. College of Transportation Engineering，Dalian Maritime University，Dalian 116026，China；2. School of Mechatronics Engineering，Shenyang Aerospace University，Shenyang 110136，China；3. School of Shipping Economic and Management，Dalian Maritime University，Dalian 116026，China) Abstract: To study the robustness of complex networks while encountering random failure or deliberate attack, the cascading failure model based on probability propagation is constructed by considering the characteristics of repeated failures and recovery of nodes. In particular, we consider that the failure probability of node decreases with the increase of number of failures and the failure probability function is constructed accordingly. Then, two kinds of node recovery strategies (i.e., probability R and stage T ) are proposed and implemented on ER random network, WS small-world network, nearest-neighbor coupled network and BA scale-free network, respectively, to test the network robustness of cascading failure model. Finally, simulation experiments are carried out and the parameters changes are considered to reveal their effects on robustness during cascading failure process. Additionally, performance tradeoff between edge robustness and node robustness is analyzed as well. The simulation results show that cascading failure scale of four types of network decreases with the increase of recovery rate. Under the stage recovery strategy, the network robustness index of four types of network shows a mutation phenomenon when the parameter T increases to a threshold. Keywords: complex network；cascading failure；probability recovery strategy；stage recovery strategy；robustness； repeated failure 0 引 言 随着对复杂网络的深入研究, 网络级联失效行 为[1-3] 及鲁棒性[4-5] 问题由于其现实意义越来越受到 研究者的广泛关注. 现实生活中, 许多复杂系统都可 以抽象为由节点和边所构成的复杂网络[6], 如病毒网 络、电网、Internet、交通网络、生物网络、供应链网络 等. 当复杂网络节点发生故障时, 通常由于其具有的 传播效应特征而引发大规模故障,甚至会导致整个网 络崩溃. 例如在病毒网络中, 流行性传染病 SARS 的 传播造成全国的恐慌; 在电网中, 电站故障会引起一 收稿日期: 2017-06-10；修回日期: 2017-12-05. 基金项目: 国家自然科学基金项目(71301108, 71201106). 责任编委: 姜斌. 作者简介: 唐亮 (1980), 男, 副教授, 博士, 从事供应链优化、复杂网络级联失效、网络化制造等研究；焦鹏(1993), 男, 硕士生, 从事复杂网络级联失效的研究. 通讯作者. E-mail: erictangliang@163.com y
    1842 控 制 与 决 策 第33卷 定规模和时间的停电事故; 在Internet 网络中, 某路由 器发生故障则会对经过该路由器的数据包进行重新 路由, 从而导致网络出现大规模的堵塞等[7-10]. 通常, 在复杂网络中某个节点发生故障时, 该节点在网络 中正常承担的功能、负载等都会通过节点间的耦合 关系分配给其邻居节点来额外承担,从而可能引起其 他节点发生新的故障甚至会导致整个网络崩溃,这种 现象称为级联失效. 对于大多数的实际网络而言, 网 络节点都具有一定的抵御风险故障能力和恢复的能 力, 当节点发生故障时, 其在网络中的部分邻居节点 会因自身拥有较强抵御风险的能力而保持正常运作 状态,其余部分邻居节点则会受到风险故障的影响而 发生级联失效,但发生故障的节点通过自我或人为修 复会使该节点恢复正常功能,并且在恢复后自身抵御 风险故障的能力会得到加强,从而使得再次发生失效 的概率降低. 目前,复杂网络级联失效方面的研究主要包括级 联失效模型[11-14]、带有应急恢复机制的级联动力学 特性[2,15] 和鲁棒性[8,16-21] 等方面. 李钊等[2] 提出了带 有应急恢复机制的网络级联失效模型, 对网络效率 和网络节点故障率进行仿真分析,发现网络效率与网 络的拓扑中节点度分布的异化程度与节点故障率有 关. 肖延东等[22] 提出了复杂网络节点负荷失效下的 可控性模型, 采用介数和 Weibull 失效模型进行仿真 分析,结果表明随机网络较之无标度网络具有较好的 可控性,同时也发现高度数节点在网络中起到了极其 重要的作用. 丁超等[23] 提出了社团划分下复杂网络 级联抗毁攻击策略, 采用介数定义节点初始负荷, 考 虑节点信息和局部择优策略对故障节点负荷重新分 配的影响,揭示了社团划分策略下对网络攻击可造成 大规模破坏的现象. 王建伟等[24] 针对复杂网络遭遇 蓄意攻击引发的级联失效问题构建了模型,对比无标 度网络和小世界网络上的全局级联失效现象,并探讨 了网络拓扑结构对边袭击策略的影响. 段东立等[25] 提出了一种可调负载重分配范围与负载重分配异质 性的复杂网络级联失效模型,并分析了该模型在无标 度网络上的级联失效条件. 王健等[26] 分析了Internet 网络级联动力学特性, 研究了不同拓扑结构、延迟时 间、处理能力、规模等的影响,从而揭示了级联失效分 为3 个阶段及影响传播的主要原因. Gao 等[27] 研究了 层间随机连接关系下关联网络之间的级联失效问题, 并解析了在随机攻击下关联网络处于稳态时其渗流 巨片的关键阈值. 邓宏钟等[28] 研究了双层小世界网 络中的级联失效行为,提出了一种带有过载函数的复 杂负载网络级联失效模型,模型给每个节点定义了一 个过载函数,用节点权值演化代替网络拓扑结构的演 化. 上述研究中,大部分研究并未考虑节点恢复这一 实际特性, 此外现实网络节点失效恢复后仍然可能 再次失效, 只是再次失效概率会有所降低, 而这些现 实特征也未体现在现有研究成果中. 为此, 本文对网 络节点设计了随故障次数增多发生故障概率逐渐降 低的故障率函数,并在概率失效的级联失效传播模式 下提出概率恢复和阶段恢复策略机制,研究级联失效 过程中不同恢复策略机制下参数的变化对网络鲁棒 性的影响. 仿真结果表明, 在概率恢复策略下, 随着恢 复率的增大, 4 类网络级联失效的规模均实现有效降 低; 而在阶段恢复策略下, 随着参数 T 值增加到不同 阈值, 4 类网络鲁棒性指标在级联失效过程中均呈现 出突变现象. 1 复杂网络级联失效模型 网络节点遭受随机故障或蓄意攻击时会以一定 的概率影响其邻居节点,实际网络中当节点发生故障 后会对其进行修复,使得节点在级联失效过程中会以 一定的概率或在一定的时刻得以恢复. 网络中发生 故障的节点恢复后,可能还会受到邻居故障节点的影 响再次发生故障. 考虑到实际网络, 如Internet、病毒 网、电网等, 当网络故障节点被修复时都会对节点抵 御风险故障的能力进行加强,所以假设在级联失效模 型中网络节点的故障率随着节点发生故障次数的增 加而降低. 因此,当模型的迭代次数达到某个临界值t 时,整个网络最终将会恢复到初始正常状态. 本文对概率恢复和阶段恢复机制下级联失效迭 代过程中网络节点和边的状态进行描述,依此研究整 个网络的综合鲁棒性. 模型中复杂网络可用一个含 有N 个节点和M 条边的图G表示,即 G = (V; E): (1) 其中: V = fv1; v2; ; vNg 为网络中节点的集合, E = f(vi; vj)jeij = 0或1g 为网络中边的集合, 当节点 vi 和节点 vj 有关联时 eij = 1, 否则 eij = 0. 根据文献 [1,27] 等对级联失效过程中迭代 (网络阶段) 的描述, 网络中故障节点 vi 向邻居节点 vj 进行概率传递即为 一次迭代(网络阶段1), 如导致邻居节点 vj 失效从而 对节点 vj 的邻居节点 vs 进行二次概率传递即为第二 次迭代(网络阶段2), 依此类推, 即为 t 次迭代(网络阶 段 t). 为了对级联失效过程进行描述, 首先对相关参 数进行如下定义: i 表示节点 vi 发生故障概率, 其中 f 为故障 f φ(xi)
    第10期 唐 亮 等: 带恢复策略的复杂网络级联失效机理及鲁棒性研究 1843 率参数(所有节点相同, 0 < f < 1); φ(xi) = xi + 1为 节点vi 发生故障次数xi 的函数; R 表示故障节点的恢复率; T 表示故障节点恢复所需阶段数目的参数; N 表示初始正常状态时网络中节点总数; M 表示初始正常状态时网络中边总数; Vt 表示 t 阶段网络中未采取恢复策略时故障节 点的总数; ′ t 表示t阶段网络中恢复节点个数; V Et 表示 t 阶段网络中未采取恢复策略时移除边 的总数; ′ t 表示t阶段网络中恢复边个数; E RIVt 表示 t 阶段网络故障节点数占原网络节点 数的比例,即节点鲁棒性指标; RIEt 表示 t 阶段网络故障边数占原网络边数的 比例,即边鲁棒性指标; RIt 表 示 t 阶 段 网 络 综 合 鲁 棒 性 指 标, RIt = RIVt + (1 )RIEt,其中 为可调参数, 0 ⩽ ⩽ 1. 1.1 概率R 恢复策略模型 网络中的节点可以分为3 种状态, 即正常运作状 态、故障状态和待恢复状态. 当网络中的节点发生故 障时, 将其正常运作状态时所承担的功能、负荷等以 一定的概率传递给其邻居节点,然后便会处于待恢复 状态不再影响其邻居节点,直至被修复到正常运作状 态,即节点每发生一次故障只会对其邻居节点造成一 次影响. 由此, 概率恢复策略下的级联失效过程描述 如下: 初始阶段, 设置故障节点, 移除与故障节点相关 联的边. 此时可知,网络节点鲁棒性指标值为 RIV1(R) = V1/N; 网络边鲁棒性指标值为 RIE1(R) = E1/M; 网络综合鲁棒性指标值为 RI1(R) = RIV1(R) + (1 )RIE1(R): 该阶段的故障节点在下阶段对其邻居节点产生影响 后会处于恢复状态,不会在之后的阶段对邻居节点产 生影响,直至其恢复到正常运作状态. 在进行 t + 1 次失效传递时, 网络节点只受到 t 次 迭代时已发生故障节点的影响,而网络节点恢复则是 面向t+1次迭代前所有的故障节点. 因此, t阶段网络 中发生故障的节点会影响其邻居节点, 并以 f φ(xi) i 的 概率致使邻居节点发生故障,同时移除与故障节点相 关联的边. 此外, t + 1 阶段之前的所有故障节点以概 率 R 恢复, 并恢复相应关联边, 此时未恢复的网络节 点仍处于待恢复状态. 因此, 该阶段网络节点鲁棒性 指标值为 RIV2(R) = (V2 V ′ 2 )/N; 边鲁棒性指标值为 RIE2(R) = (E2 E ′ 2)/M; 网络综合鲁棒性指标值为 RI2(R) = RIV2(R) + (1 )RIE2(R): 重复迭代,直至整个网络恢复到初始正常状态. 1.2 阶段T 恢复策略模型 考虑到另外一些实际的网络, 如交通网络、供应 链网络等,当网络节点发生故障后需要在规定的时刻 恢复正常运作功能,此时采用概率恢复策略无法体现 网络节点限时恢复这一特性. 因此, 考虑网络节点发 生故障后经过一定阶段的恢复策略, 采用参数 T 表征 节点恢复的阶段数(即任意节点发生故障后需经过 T 个阶段才能恢复). 该恢复策略下的级联失效过程描 述如下: 在初始阶段, 针对初始故障节点, 移除与其相关 联的边. 此时可知,网络节点鲁棒性指标值为 RIV1(T ) = V1/N; 边鲁棒性指标值为 RIE1(T ) = E1/M; 网络综合鲁棒性指标值为 RI1(T ) = RIV1(T ) + (1 )RIE1(T ): 同时, 该阶段发生故障的节点需要经过 T 个阶段后在 T + 1阶段时恢复正常运作功能. 初始阶段后, 与概率 R 恢复策略类似, 前一阶段 中发生故障的节点会影响其邻居节点, 并以 f φ(xi) i 的 概率致使邻居节点发生故障,同时移除与故障节点相 关联的边. 另外, 恢复在当前阶段达到所需恢复阶段 数 T 的待恢复节点, 此时与恢复节点相关联的边也随 之恢复, 而未恢复的节点将仍将处于待恢复状态. 此 时,网络节点鲁棒性指标值为 RIV2(T ) = (V2−V ′ 2 )/N; 边鲁棒性指标值为 RIE2(T ) = (E2−E ′ 2)/M; 网络综合鲁棒性指标值为 RI2(T ) = RIV2(T ) + (1 )RIE2(T ): 重复执行该迭代过程,直至整个网络恢复到初始正常 状态.
    1844 2 数值仿真 控 制 与 决 策 第33卷 为使研究结果更具普适性, 本文构建4 类网络进 行级联失效过程中网络鲁棒性的仿真分析: ER 随机 网络、WS 小世界网络、NC 最近邻耦合网络和BA 无 标度网络. 每类网络采用1 000 个节点, 平均度⟨k⟩ = 6, 参数 取值0.8, 对模型综合鲁棒性进行100 次仿真 取平均值. 2.1 概率恢复策略仿真分析 对级联失效模型采用概率恢复策略机制,研究恢 复率 R 值变化和故障率参数 f 变化时网络综合鲁棒 性指标RIt 的相应变化情况. 2.1.1 恢复率R 值变化 设定参数 f 初始值为0.8, 恢复率 R 值按0.1、0.3、 0.5、0.7、0.9 变化, 对4 类网络级联失效模型的综合恢 复鲁棒性指标值进行仿真. 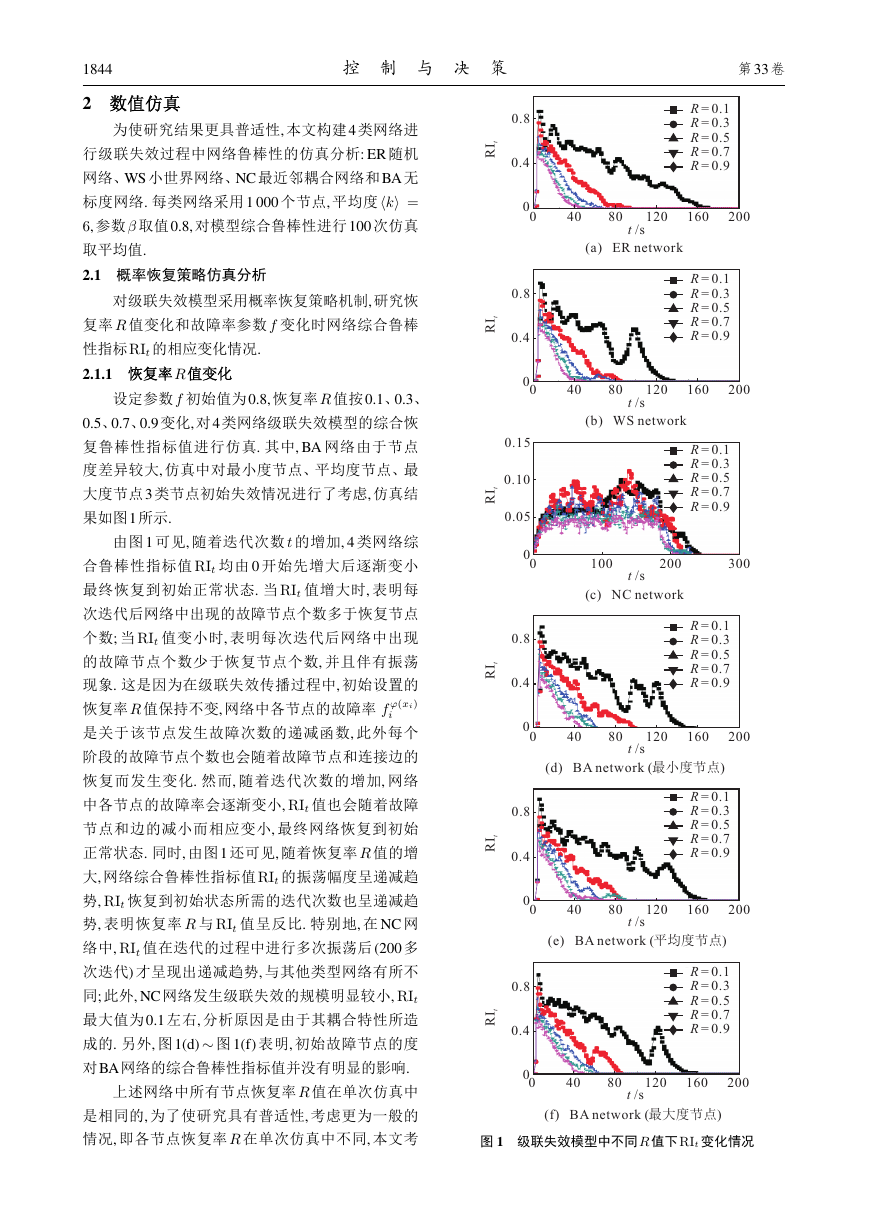其中, BA 网络由于节点 度差异较大, 仿真中对最小度节点、平均度节点、最 大度节点3 类节点初始失效情况进行了考虑, 仿真结 果如图1所示. i 由图 1 可见, 随着迭代次数 t 的增加, 4 类网络综 合鲁棒性指标值 RIt 均由 0 开始先增大后逐渐变小 最终恢复到初始正常状态. 当 RIt 值增大时, 表明每 次迭代后网络中出现的故障节点个数多于恢复节点 个数; 当 RIt 值变小时, 表明每次迭代后网络中出现 的故障节点个数少于恢复节点个数, 并且伴有振荡 现象. 这是因为在级联失效传播过程中, 初始设置的 恢复率 R 值保持不变, 网络中各节点的故障率 f φ(xi) 是关于该节点发生故障次数的递减函数, 此外每个 阶段的故障节点个数也会随着故障节点和连接边的 恢复而发生变化. 然而, 随着迭代次数的增加, 网络 中各节点的故障率会逐渐变小, RIt 值也会随着故障 节点和边的减小而相应变小, 最终网络恢复到初始 正常状态. 同时, 由图1 还可见, 随着恢复率 R 值的增 大, 网络综合鲁棒性指标值RIt 的振荡幅度呈递减趋 势, RIt 恢复到初始状态所需的迭代次数也呈递减趋 势, 表明恢复率 R 与 RIt 值呈反比. 特别地, 在 NC 网 络中, RIt 值在迭代的过程中进行多次振荡后(200 多 次迭代) 才呈现出递减趋势, 与其他类型网络有所不 同; 此外, NC 网络发生级联失效的规模明显较小, RIt 最大值为0.1 左右, 分析原因是由于其耦合特性所造 成的. 另外, 图 1(d) 图 1(f) 表明, 初始故障节点的度 对BA网络的综合鲁棒性指标值并没有明显的影响. 上述网络中所有节点恢复率 R 值在单次仿真中 是相同的, 为了使研究具有普适性, 考虑更为一般的 情况, 即各节点恢复率 R 在单次仿真中不同, 本文考 图 1 级联失效模型中不同 R 值下RIt 变化情况 04080120160200t/s(a) ER network04080120160200t/s(b)WS network0100200300t/s(c) NC network04080120160200t/s(d) BAnetwork ()ᨬ⁚F04080120160200t/s(e)BAnetwork ()ᙳ⁚F04080120160200t/s(f)BAnetwork ()ᨬᜧ⁚F00.40.8RIt00.40.8RIt00.050.100.15RIt00.40.8RIt00.40.8RIt00.40.8RItR=0.1R=0.3R=0.5R=0.7R=0.9R=0.1R=0.3R=0.5R=0.7R=0.9R=0.1R=0.3R=0.5R=0.7R=0.9R=0.1R=0.3R=0.5R=0.7R=0.9R=0.1R=0.3R=0.5R=0.7R=0.9R=0.1R=0.3R=0.5R=0.7R=0.9
    第10期 唐 亮 等: 带恢复策略的复杂网络级联失效机理及鲁棒性研究 1845 虑两种恢复率策略: 所有节点随机概率恢复; 节点恢 复率与其初始度相关. 两种策略下的4 类网络综合鲁 棒性仿真结果如图2所示. 图 2 不同概率恢复策略下4 种网络RIt 变化情况 由图 2(a) 可见, 当所有节点恢复率为随机时, 除 了 NC 网络因其网络结构特性其鲁棒指标值与其他 网络表现有所不同, 其他3 类网络的鲁棒性指标在级 联失效过程中差异并不是特别大,表明该种策略下网 络结构对于综合鲁棒性的影响不大. 而在节点恢复 率与其初始度 K 呈 RK 关系时(度大的故障节点通常 由于连接关系的复杂性其恢复率会相应较低), 4类网 络的鲁棒性指标在级联失效过程中呈现出较大的差 异. 相对而言, 初始故障点为最小度节点的 BA 网络 在初始迭代过程中呈现更好的鲁棒性, 而WS 网络则 在迭代的后期更快地恢复到正常网络状态,表明该策 略下,网络结构对鲁棒性有较大影响. 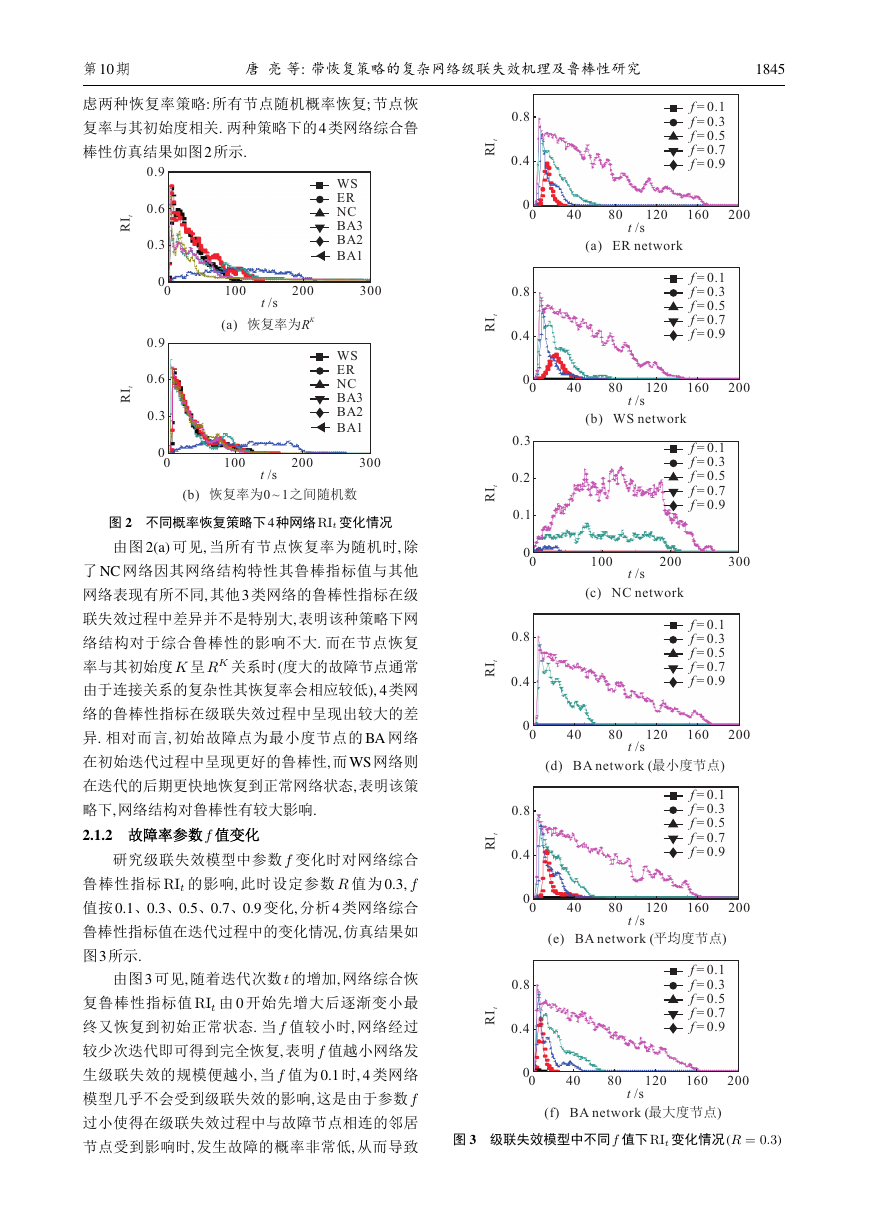2.1.2 故障率参数f 值变化 研究级联失效模型中参数 f 变化时对网络综合 鲁棒性指标 RIt 的影响, 此时设定参数 R 值为 0.3, f 值按0.1、0.3、0.5、0.7、0.9 变化, 分析4 类网络综合 鲁棒性指标值在迭代过程中的变化情况,仿真结果如 图3所示. 由图3 可见, 随着迭代次数 t 的增加, 网络综合恢 复鲁棒性指标值 RIt 由 0 开始先增大后逐渐变小最 终又恢复到初始正常状态. 当 f 值较小时, 网络经过 较少次迭代即可得到完全恢复, 表明 f 值越小网络发 生级联失效的规模便越小, 当 f 值为 0.1 时, 4 类网络 模型几乎不会受到级联失效的影响, 这是由于参数 f 过小使得在级联失效过程中与故障节点相连的邻居 节点受到影响时, 发生故障的概率非常低, 从而导致 图 3 级联失效模型中不同 f 值下RIt 变化情况(R = 0:3) 0100200300t/s(a)ឮɎ᳛KR0100200300t/s(b)ឮɎ᳛0~1_ψʡᦪ00.30.60.9RIt00.30.60.9RItWSERNCBA3BA2BA1WSERNCBA3BA2BA104080120160200t/s(a) ER network04080120160200t/s(b)WS network0100200300t/s(c) NC network04080120160200t/s(d) BAnetwork ()ᨬ⁚F04080120160200t/s(e)BAnetwork ()ᙳ⁚F04080120160200t/s(f)BAnetwork ()ᨬᜧ⁚F00.40.8RIt00.40.8RIt00.10.20.3RIt00.40.8RIt00.40.8RIt00.40.8RItf=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9
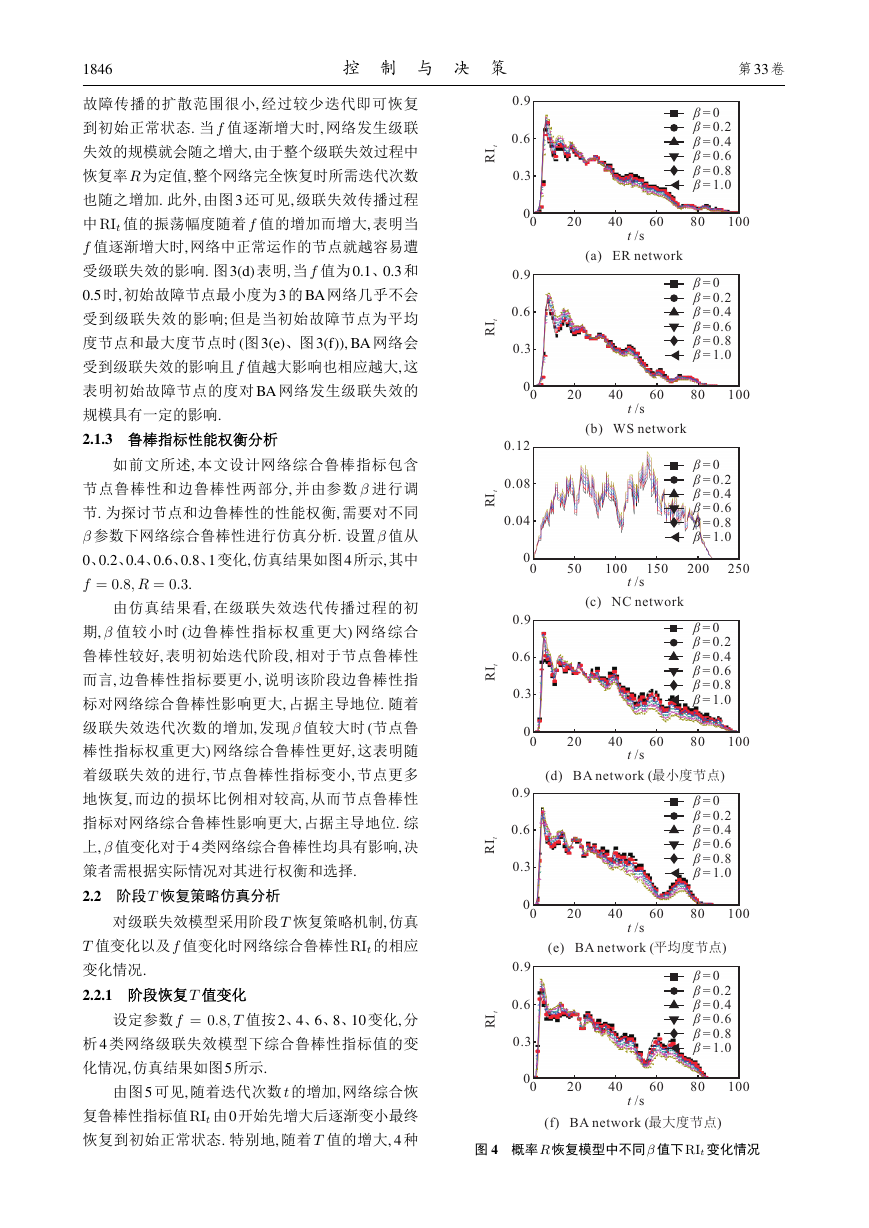
    1846 控 制 与 决 策 第33卷 故障传播的扩散范围很小, 经过较少迭代即可恢复 到初始正常状态. 当 f 值逐渐增大时, 网络发生级联 失效的规模就会随之增大,由于整个级联失效过程中 恢复率 R 为定值,整个网络完全恢复时所需迭代次数 也随之增加. 此外, 由图3 还可见, 级联失效传播过程 中RIt 值的振荡幅度随着 f 值的增加而增大, 表明当 f 值逐渐增大时, 网络中正常运作的节点就越容易遭 受级联失效的影响. 图3(d) 表明, 当 f 值为0.1、0.3 和 0.5 时, 初始故障节点最小度为3 的BA 网络几乎不会 受到级联失效的影响; 但是当初始故障节点为平均 度节点和最大度节点时(图3(e)、图3(f)), BA 网络会 受到级联失效的影响且 f 值越大影响也相应越大, 这 表明初始故障节点的度对 BA 网络发生级联失效的 规模具有一定的影响. 2.1.3 鲁棒指标性能权衡分析 如前文所述, 本文设计网络综合鲁棒指标包含 节点鲁棒性和边鲁棒性两部分, 并由参数 进行调 节. 为探讨节点和边鲁棒性的性能权衡, 需要对不同 参数下网络综合鲁棒性进行仿真分析. 设置 值从 0、0.2、0.4、0.6、0.8、1变化,仿真结果如图4所示,其中 f = 0:8; R = 0:3. 由仿真结果看, 在级联失效迭代传播过程的初 期, 值较小时 (边鲁棒性指标权重更大) 网络综合 鲁棒性较好, 表明初始迭代阶段, 相对于节点鲁棒性 而言, 边鲁棒性指标要更小, 说明该阶段边鲁棒性指 标对网络综合鲁棒性影响更大, 占据主导地位. 随着 级联失效迭代次数的增加, 发现 值较大时 (节点鲁 棒性指标权重更大) 网络综合鲁棒性更好, 这表明随 着级联失效的进行, 节点鲁棒性指标变小, 节点更多 地恢复, 而边的损坏比例相对较高, 从而节点鲁棒性 指标对网络综合鲁棒性影响更大, 占据主导地位. 综 上, 值变化对于4 类网络综合鲁棒性均具有影响, 决 策者需根据实际情况对其进行权衡和选择. 2.2 阶段T 恢复策略仿真分析 对级联失效模型采用阶段 T 恢复策略机制, 仿真 T 值变化以及 f 值变化时网络综合鲁棒性RIt 的相应 变化情况. 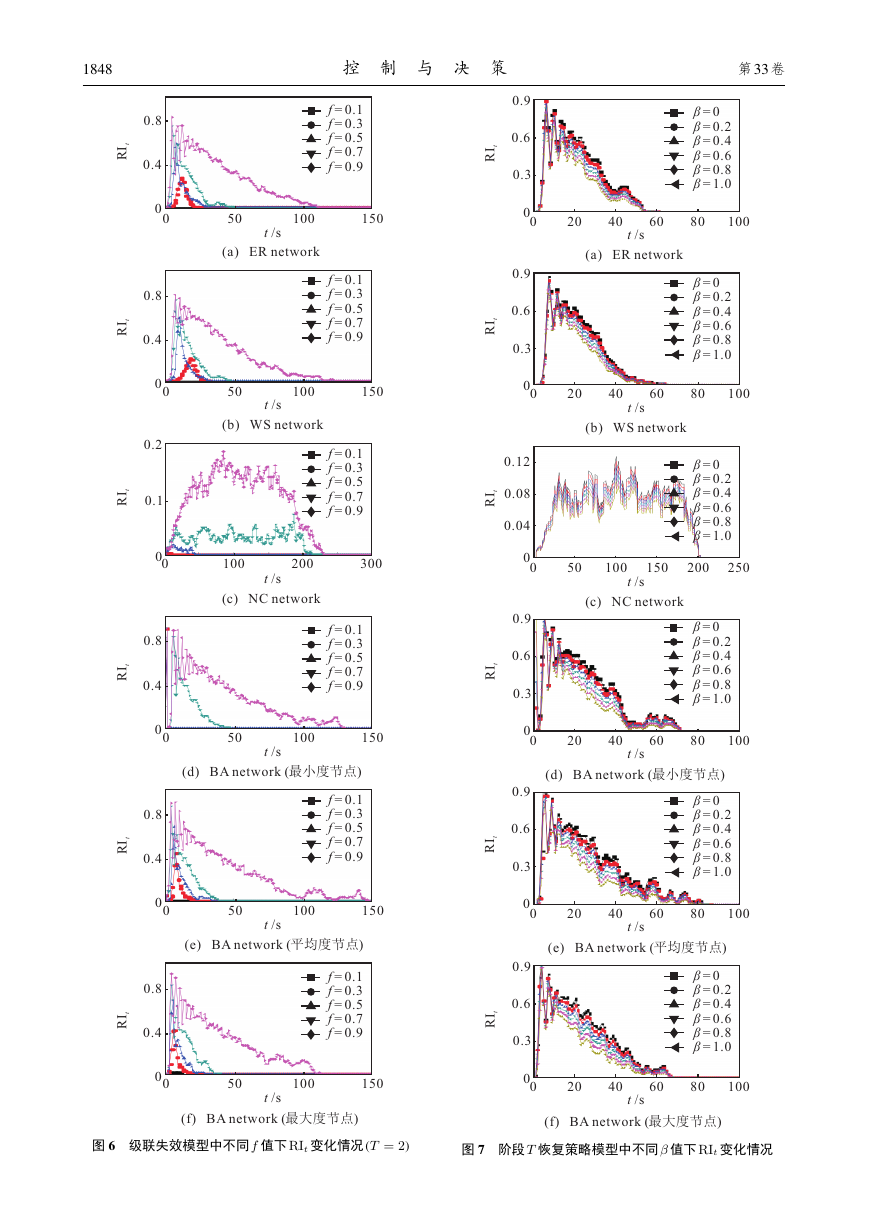2.2.1 阶段恢复T 值变化 设定参数 f = 0:8; T 值按2、4、6、8、10 变化, 分 析 4 类网络级联失效模型下综合鲁棒性指标值的变 化情况,仿真结果如图5所示. 由图5 可见, 随着迭代次数 t 的增加, 网络综合恢 复鲁棒性指标值RIt 由0开始先增大后逐渐变小最终 恢复到初始正常状态. 特别地, 随着 T 值的增大, 4 种 图 4 概率 R 恢复模型中不同 值下RIt 变化情况 020406080100t/s(a) ER network(b)WS network(c) NC network(d) BAnetwork ()ᨬ⁚F(e)BAnetwork ()ᙳ⁚F(f)BAnetwork ()ᨬᜧ⁚F020406080100t/s020406080100t/s020406080100t/s020406080100t/s050100150200250t/s00.30.60.9RIt00.30.60.9RIt00.30.60.9RIt00.30.60.9RIt00.30.60.9RIt00.040.080.12RItβ=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4
    第10期 唐 亮 等: 带恢复策略的复杂网络级联失效机理及鲁棒性研究 1847 网络模型中的RIt 值均呈现有突变现象, 在ER 和NC 网络模型中发现, 当 T 值由 4 变为 6 时, 图像中的 RIt 值呈现有突变现象. 这表明, 当 T = 6 时, 由于恢复阶 段数较长,这两类网络中待恢复状态节点无法及时恢 复, 经过几次迭代网络中节点几乎全部损坏. 然而, 刚 开始恢复时网络中大部分节点处于待恢复状态, 无 法产生更大规模的故障, 从而使网络快速恢复到初 始状态. 而当 T > 6 时, 随着 T 值的增加, 网络综合 鲁棒性指标自拐点后也相应逐渐增大, 但增幅很小, 这是由于此时网络中节点几乎全部损坏的特性所导 致. 类似地, 在WS 网络模型中发现, 当 T 值由6 变为8 时, 图像中的RIt 值呈现有突变现象; 在BA 网络模型 中发现当 T 值由2 变为4 时, 图像中的RIt 值呈现有突 变现象. 这些突变现象是由于采用阶段 T 恢复策略 时, 起初小于 T 值的迭代过程中故障节点不能及时恢 复所造成. 另外可知, NC 网络模型中的RIt 值在级联 失效过程中的振荡频率和持续时间远大于其他 3 种 网络, 且级联失效规模远小于其他 3 种网络, 这是由 于NC 网络的耦合特性所造成的. 同时由图5 还可见, 随着迭代次数 t 的增加, 网络综合恢复鲁棒性指标值 RIt 的振荡频率呈递减趋势, 表明网络节点及连接边 在级联失效过程中逐渐趋于稳定. 此外, 图 5(d) 图 5(f) 表明, 当阶段恢复 T 值变化时, 初始故障节点的度 对BA网络综合鲁棒性指标值并没有明显的影响. 2.2.2 故障率参数f 值变化 设定参数 T = 2; f 值按0.1、0.3、0.5、0.7、0.9 变 化,分析各网络级联失效模型下综合鲁棒性指标值的 变化情况,仿真结果如图6所示. 由图6 可见, 随着迭代次数 t 的增加, 网络综合鲁 棒性指标值RIt 呈现先增后减的变化趋势. 与概率恢 复策略下的情况类似, 随着 t 值的增加, 网络发生级联 失效的规模逐渐增大, 且网络综合鲁棒性指标值RIt 的振荡频率和幅度也在增大; 当 f 值较小时,RIt 值经 过较少次的迭代即可恢复到初始状态. 此外, 由图 6 还可见, 当 f 值等于0.1 和0.3 时, 4 种网络模型受到级 联失效的影响非常小,其原因与概率恢复策略下的仿 真结果分析类似. 而图 6(d) 图 6(f) 表明, 阶段 T 恢 复策略下, 初始故障节点的度对BA 网络发生级联失 效的规模具有一定的影响. 2.2.3 鲁棒指标性能权衡分析 考虑阶段 T 恢复策略下参数 值变化时, 节点和 边鲁棒性的性能权衡. 设置 值从0、0.2、0.4、0.6、0.8、 1 变化, 网络综合鲁棒性指标仿真结果如图7 所示, 其 中f = 0:8; T = 2. 图 5 级联失效模型中不同 T 值下RIt 变化情况 050100150(a) ER network(b)WS network(c) NC network(d) BAnetwork ()ᨬ⁚F(e)BAnetwork ()ᙳ⁚F(f)BAnetwork ()ᨬᜧ⁚Ft/st/st/st/st/st/s050100150010020030002040608010002040608010002040608010000.40.8RIt00.40.8RIt00.050.10RIt00.40.8RIt00.40.8RIt00.40.8RItT=2T=4T=6T=8T=10T=2T=4T=6T=8T=10T=2T=4T=6T=8T=10T=2T=4T=6T=8T=10T=2T=4T=6T=8T=10T=2T=4T=6T=8T=10
    1848 控 制 与 决 策 第33卷 图 6 级联失效模型中不同 f 值下RIt 变化情况(T = 2) 图 7 阶段 T 恢复策略模型中不同 值下RIt 变化情况 050100150(a) ER network(b)WS network(c) NC network(d) BAnetwork ()ᨬ⁚F(e)BAnetwork ()ᙳ⁚F(f)BAnetwork ()ᨬᜧ⁚Ft/st/st/st/st/st/s050100150050100150050100150050100150010020030000.40.8RIt00.40.8RIt00.10.2RIt00.40.8RIt00.40.8RIt00.40.8RItf=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9f=0.1f=0.3f=0.5f=0.7f=0.9020406080100t/s(a) ER network(b)WS network(c) NC network(d) BAnetwork ()ᨬ⁚F(e)BAnetwork ()ᙳ⁚F(f)BAnetwork ()ᨬᜧ⁚F020406080100t/s020406080100t/s020406080100t/s020406080100t/s050100150200250t/s00.30.60.9RIt00.30.60.9RIt00.30.60.9RIt00.30.60.9RIt00.30.60.9RIt00.040.080.12RItβ=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4β=0β=0.2β=0.8β=0.6β=1.0β=0.4
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料