logo资料库

SVD推荐算法教程.pptx

发布时间：2022-06-16 发布人：admin 分类：说明书 资料大小：0.45M 资料格式：pptx 举报 版权申诉
第1页 / 共35页
第2页 / 共35页
第3页 / 共35页
第4页 / 共35页
第5页 / 共35页
第6页 / 共35页
第7页 / 共35页
第8页 / 共35页
资料共35页，剩余部分请下载后查看
    SVD 特征值 奇异值
    Netflix Prize背景介绍  目标：  数据结构：  训练数据： ³ 悬赏100万美元，将Netflix的推荐算法预测准确度提高10%。 ³ 用户ID、电影名称、日期、分数（1-5之间的整数） ³48万用户对两万部电影的上亿条评分 ³ 包括一个与测试数据集分布相同的probe数据集，包含06年附近140多万条的 数据点，每个用户至少对9部电影进行了打分，服从正态分布。 ³280万个数据点（隐藏的，参赛选手不能获得，并且参赛选手自己也不能获得 CineMatch精度：0.951 自己模型作用在测试数据集上的最终效果）  评测标准：均方误差根  测试数据：
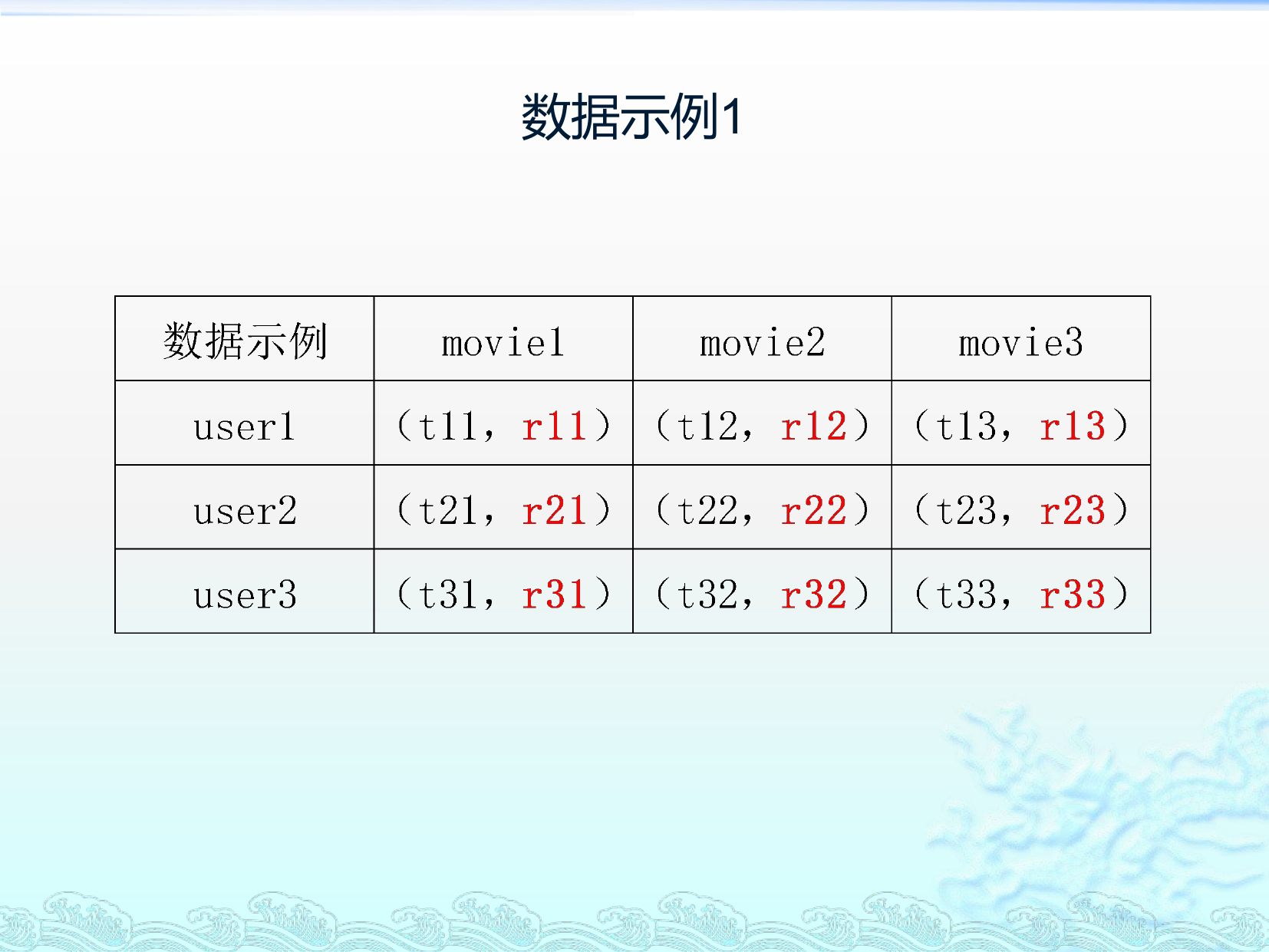
    数据示例1
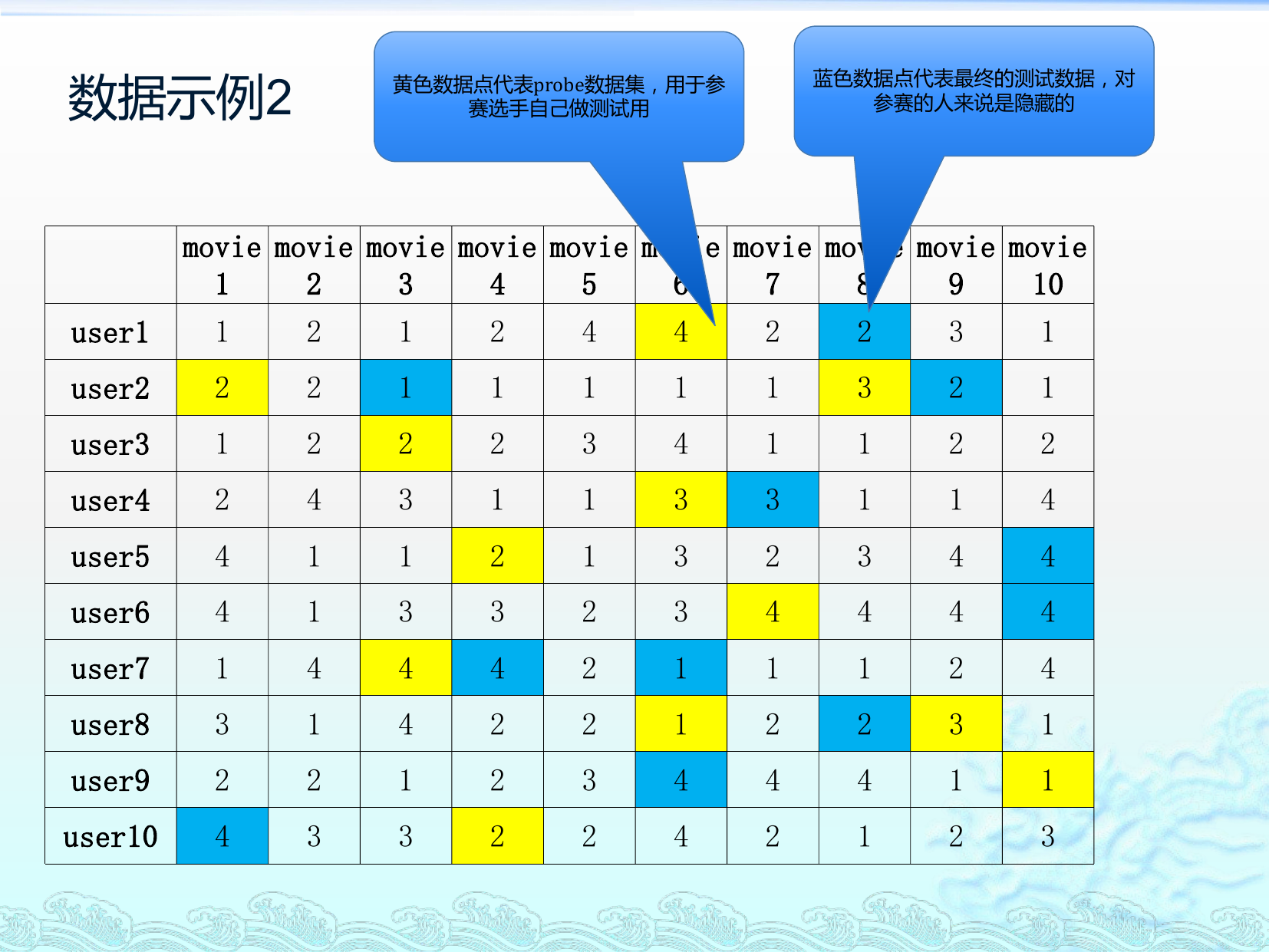
    数据示例2 黄色数据点代表probe数据集，用于参 赛选手自己做测试用 蓝色数据点代表最终的测试数据，对 参赛的人来说是隐藏的 　 movie 1 user1 user2 user3 user4 user5 user6 user7 user8 user9 user10 1 2 1 2 4 4 1 3 2 4 movie movie movie movie movie movie movie movie movie 2 2 2 2 4 1 1 4 1 2 3 3 1 1 2 3 1 3 4 4 1 3 4 2 1 2 1 2 3 4 2 2 2 5 4 1 3 1 1 2 2 2 3 2 6 4 1 4 3 3 3 1 1 4 4 7 2 1 1 3 2 4 1 2 4 2 8 2 3 1 1 3 4 1 2 4 1 9 3 2 2 1 4 4 2 3 1 2 10 1 1 2 4 4 4 4 1 1 3
     矩阵运算（1） a a  11 1 n    a a 1 mn m ka ka 11 1 n    ka ka 1 m        mn =           k 数乘：      +            b b 11 1 n    b b 1 mn m  =           a 11 a 1 m +  + b 11 b 1 m    a 1 n a mn +  + b 1 n b mn      加法： a a   11 1 n       a a   1 mn m 乘法： a a  12 11  a a  22 21  a a  32 31         b 1 1 b 21 b 12 b 22 b 13 b 23    =      c 11 c 21 c 31 c 12 c 22 c 32 c 13 c 23 c 33      , = c ij a b 1 1 i + a b 2 i j j 2
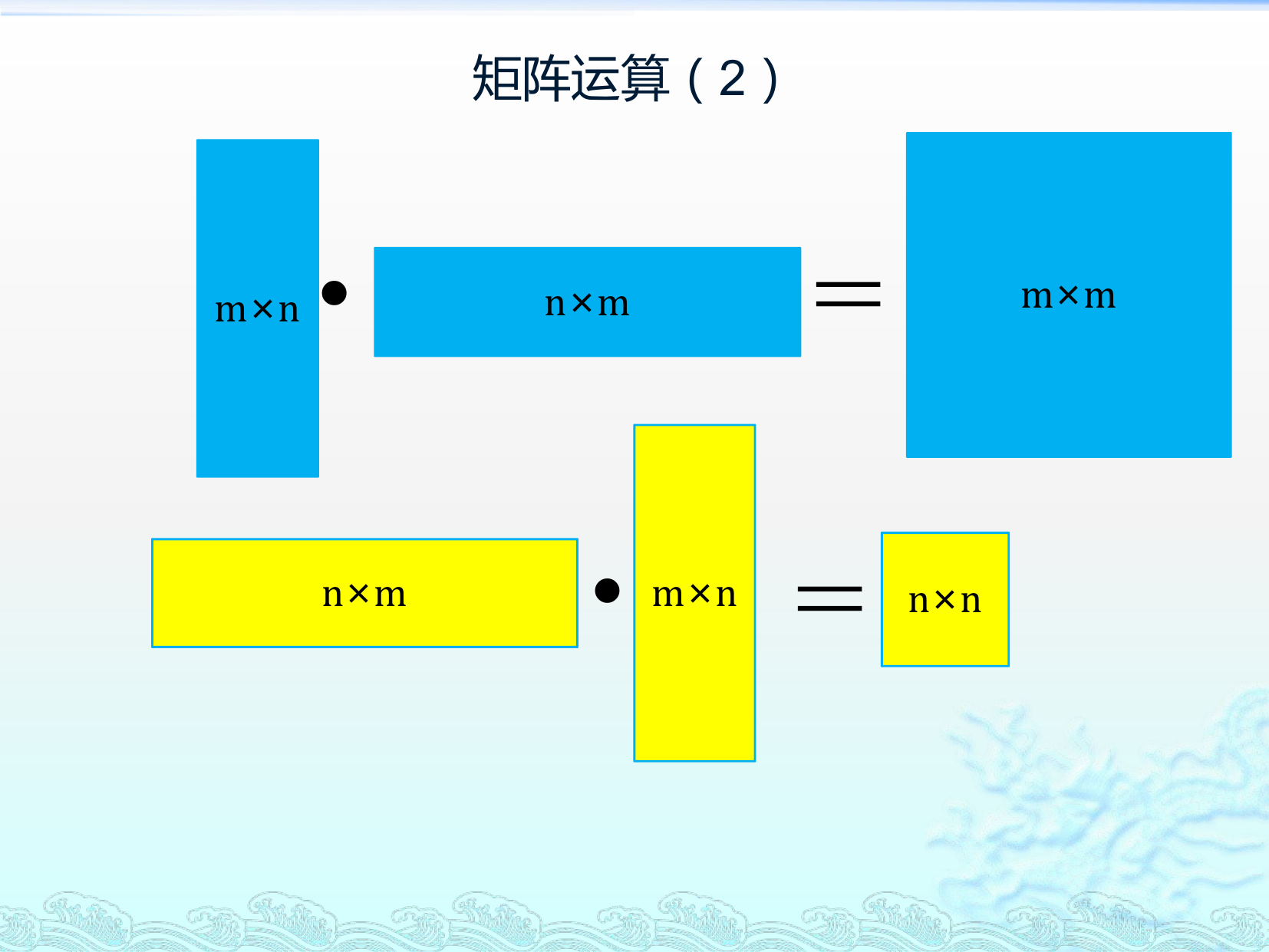
    矩阵运算（2）  m×n n×m = m×m n×m  m×n = n×n
    矩阵运算（3） a       b   c    x y z = ax ay az bx by bz cx cy cz             a b c x     y     z   = + + ax by cz
    线性空间  线性空间：“客观”存在的一种空间，对加法和数乘具 有封闭性。  向量：既有大小又有方向的量，同时没有起点  线性空间的基：描述空间内向量的一组“特殊”的向量， 空间内的所有向量都能被一组基的线性组合表示。  举例：直线就是一维的线性空间，平面就是二维线性空 间，三维立体空间就是三维线性空间。
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料