logo资料库

密码学实验4 RSA加密算法实现报告.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：1.19M 资料格式：doc 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    School of Software, Yunnan University
    云南大学软件学院 School of Software, Yunnan University 成绩 学 期: 2011 秋季学期 课程名称: 密码技术 任课教师: 学生姓名: 学 号: 实验项目: 实验四实现 RSA 算法的加解密 联系电话: 电子邮件: 完成提交时间： 年 月 日
    密码技术实验报告 实验项目：实验四，实现 RSA 对任意文件的加解密 实现 RSA 对任意文件的加解密（命令行方式） 加解密形式如下： 实验要求 （内容） RSA -e/-d keyfile inputfile outputfile 说明：产生 rsa 的公私钥，可以分别放入 keyfile 中，n 至少为 32bit，构建 rsa 加密算法。对于加密来说，输入文件名就是明文文件，对于解密来说，输入文 件名就是密文文件，注意加密对应公钥，解密对应私钥，注意文件读取方式和控 制文件结束 控制台编程： int main(int argc, char *argv[ ]) 操作系统：win7 实验环境 编译环境：Microsoft Visual Studio 2010 本次实验达到了题目的要求： 实现功能 实现用 RSA 算法利用控制台对任意文件的加解密，用键盘接收明文（密文） 文件路径和密钥，然后再输入需要保存的密文（明文）文件路径，然后就可以把 加解密后得到的密明文文件保存该路径下。另外还实现了 RSA 密钥对的生成其中 N 的长度为 32bit，并能够将生成的密钥对保存在文件，还能够把文件中的密钥对 导入到程序中。 主函数的操作也充分体现了程序的可操作性和健壮性，能够让用户自己选择 相应的操作，比如生成密钥对、导入密钥对、加密、解密以及对程序的一些基本 情况说明。 但是对文件的路径的输入有比较严格的格式约束。如：盘符名：\\文件名.txt 格 式错误则会导致文件打开失败，不能进行加解密操作。另外生成的密钥对长度较 小，安全性不是很理想。 数据结构 本次实验的算法实现比较简单，在实验过程中用到的主要数据结构为数组和 文件型指针，在实验中我定义了2个文件型指针FILE *fp1,*fp2，其中一个指向明 文文件，一个指向密文文件。另外还定义了多个字符数组，如char Plainfpath[260] 声明字符数组存储明文文件的文件路径，char Cipherfpath[260]声明字符数组存储 密文文件的文件路径。在程序中声明了unsigned long long类型的数据用于存储生 成的随机大素数。还声明了unsigned long long Plain[2]的数组用于存储明文字符。
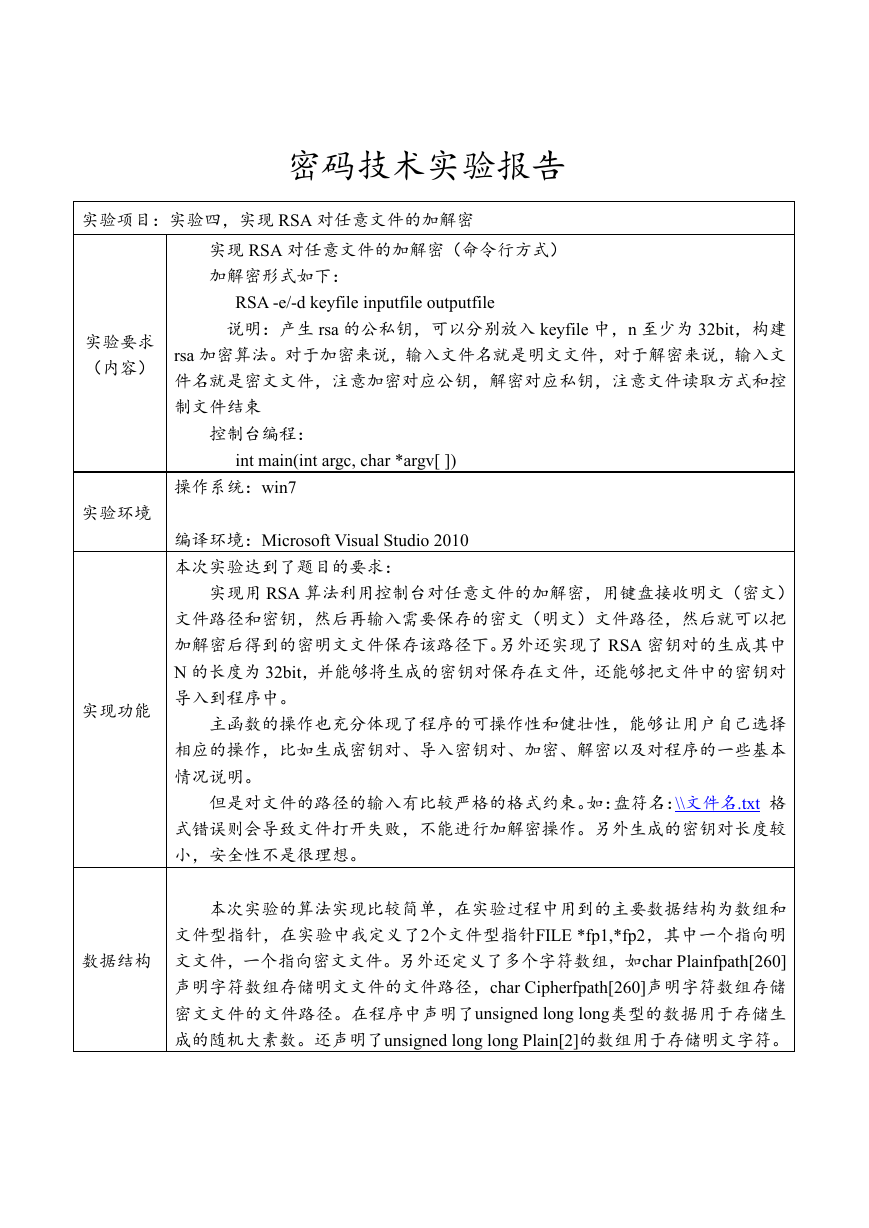
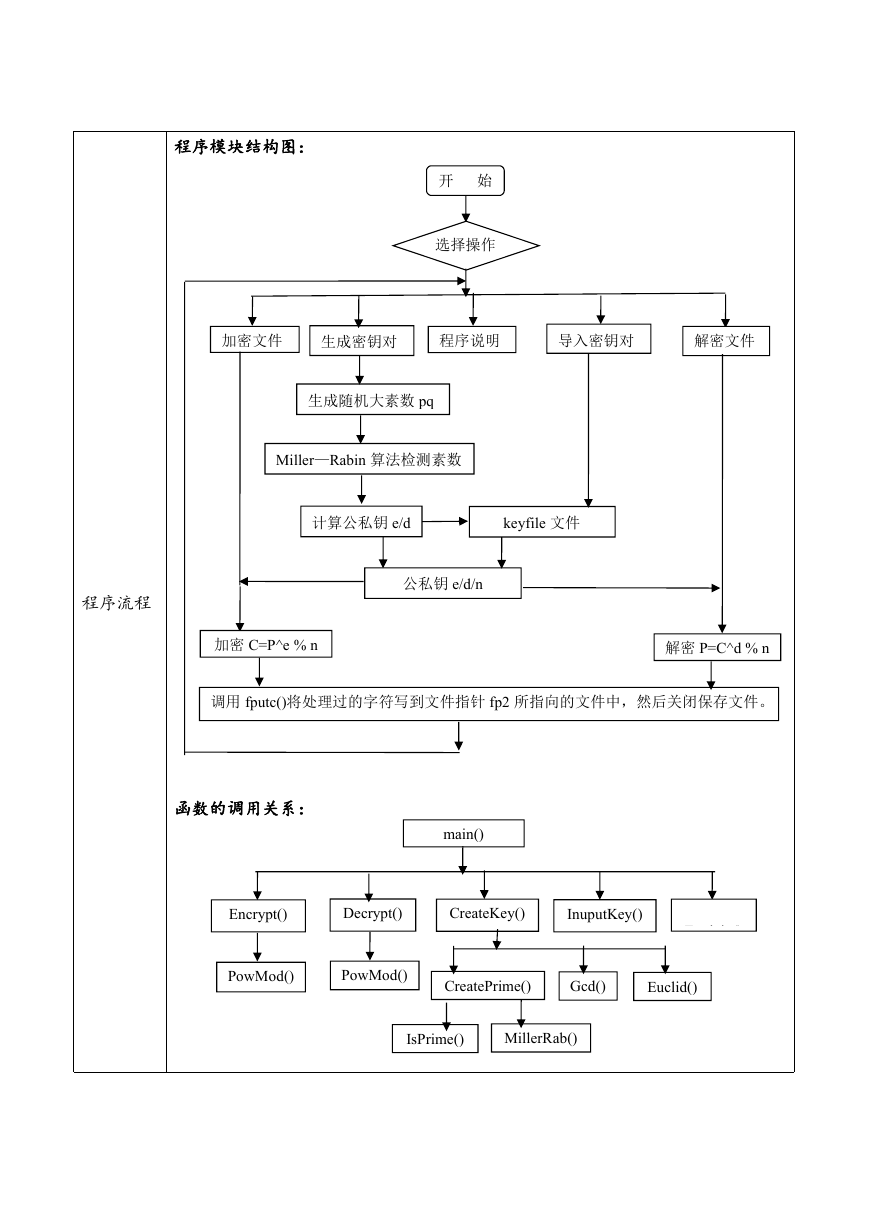
    程序模块结构图： 开 始 start 选择操作 加密文件 生成密钥对 程序说明 导入密钥对 解密文件 生成随机大素数 pq Miller—Rabin 算法检测素数 计算公私钥 e/d keyfile 文件 程序流程 公私钥 e/d/n 加密 C=P^e % n 解密 P=C^d % n 调用 fputc()将处理过的字符写到文件指针 fp2 所指向的文件中，然后关闭保存文件。 函数的调用关系： main() Encrypt() Decrypt() CreateKey() InuputKey() Explain() PowMod() PowMod() CreatePrime() Gcd() Euclid() IsPrime() MillerRab()
    函数的接口： unsigned long long PowMod(unsigned long long a,unsigned long x,unsigned long n);// 模幂运算 unsigned long CreatePrime();//生成大素数 unsigned long MillerRab(int n);//Miller—Rabin 算法 int IsPrime(int n);//检测大素数 unsigned long Gcd(unsigned long e, unsigned long n);//欧拉定理求 e unsigned long Euclid( unsigned long e,unsigned long fn,unsigned long 展的欧几里得算法求 d unsigned long CreateKey();//生成密钥对 unsigned long InputKey();//导入密钥对 void Encrypt(unsigned long e, unsigned long n);//RSA 加密算法 void Decrypt(unsigned long d, unsigned long n);//RSA 解密算法 void Explain(); //程序说明函数 *result);//扩
    主要函数的接口、调用与被调用函数、所实现的功能和实现的主要思路： int main(char ch) ： Function: Calls: 为用户提供基本操作，调用函数生成密钥对和加解密文件。 CreateKey()、InputKey()、Encrypt()、Decrypt 和 Explain() Called By: 无 Input(type) 字符型（char） Output(type): 无，只是输出“”中的字符串。 Return(type): 整型 Others: Bug: 无 测试尚未发现 void CreateKey() Function: 实现的功能是：生成公私密钥对并保存在文件中。 代 码 与 代 码分析 实现的主要思路：随机生成大素数 p 和 q，然后根据欧拉函数求得 n=（p-1） *（q-1），再根据欧拉定理，gcd(e,n)=1 求得公钥 e；然后根据扩展欧几里得算法求 私钥 d，组成公私密钥对。 Calls: CreatePrime()、Gcd()和 Euclid() Called By: main() Input(type) unsigned long 类型的随机大素数 p/q Output(type): unsigned long 类型的数 e/d/n Return(type): unsigned long Others: Bug: 无 测试中尚未发现 void InputKey() Function: 实现的功能是：将 Keyfile 文件中的公私密钥导入到程序中。 Calls: 无
    Called By: main() Input(type) char 类型的字符数组 Output(type): unsigned long 类型的数 e/d/n Return(type): unsigned long Others: Bug: 无 测试中尚未发现 void Encrypt(unsigned long e, unsigned long n); Function: 实现的功能是：接受明密文文件的文件路径输入，然后根据 RSA 加密算法 C=P^e mod n 生成密文并保存在文件中。 实现的主要思路：根据生成的密钥对 e/d/n 的值，然后根据加密算法 C=P^e mod n 求得密文字符并保存在文件中。 Calls: PowMod() Called By: main() Input(type) char 类型的数组和 unsigned long 类型的字符 Output(type): unsigned long 类型的字符 Return(type): 无 Others: Bug: 无 测试中尚未发现 void Decrypt(unsigned long d, unsigned long n); Function: 实现的功能是：接受明密文文件的文件路径输入，然后根据 RSA 解密算法 P=C^d mod n 生成明文并保存在文件中。 实现的主要思路：根据生成的密钥对 e/d/n 的值，然后根据加密算法 P=C^d mod n 求得密文字符并保存在文件中。 Calls: PowMod() Called By: main()
    Input(type) char 类型的数组和 unsigned long 类型的字符 Output(type): unsigned long 类型的字符 Return(type): 无 Others: Bug: 无 测试中尚未发现 unsigned long CreatePrime() Function: 实现的功能是：生成一个长度为 16bit 的大素数。 实现的主要思路：随机产生一个大数，在进行后面的素数判别时会比较耗时， 所以，在把大数送入到素数判别程序前，将一些容易判别出的合数过滤掉。这里 采用大数除以小素数过滤掉一部分合数 ，选取 50 个小素数进行对大数的过滤。 Calls: 无 Called By: CreateKey() Input(type) 无 Output(type): 无 Return(type): unsigned long Others: Bug: 无 测试中尚未发现 unsigned long MillerRab(int n) Function: 实现的功能是：利用 Miller-Rabin 算法检测生成的大素数的素性。 实现的主要思路：先计算出 m、j，使得 n-1=m*2^j，其中 m 是正奇数，j 是 非负整数，然后随机取一个 a，2<=a，再计算 v=a^m mod n，如果 v==1，通过测 试，返回；令 i=1；如果 v=n-1，通过测试，返回；如果 i==j，非素数，结束；v=v^2 mod n，i=i+1 一直循环取 5 个值。 Calls: 无 Called By: IsPrime()
    Input(type) unsigned long 的随机大素数 Output(type): 无 Return(type): unsigned long 1 或 0 Others: Bug: 无 测试中尚未发现 unsigned long Gcd(unsigned long e, unsigned long n) Function: 实现的功能是：计算出一个与 n 互素的素数 e 作为公钥 实现的主要思路：根据欧拉定律，对任意互素的 e 和 n，有 e^Φ(n) =1(mod n)， 求出的 e 就可以作为私钥，具体的实现算法如下： if(e < n){ unsigned long t=n; n=e; e=t;} if(n == 0) return e; else Gcd(n,e%n); Calls: 无 Called By: CreateKey() Input(type) unsigned long Output(type): unsigned long Return(type): unsigned long Others: Bug: 无 测试中尚未发现 unsigned long Euclid( unsigned long e,unsigned long fn,unsigned long *result) Function: 实现的功能是：根据扩展的欧几里得定律求出私钥 d 实现的主要思路：根据扩展的欧几里得定律，对任意互素的 e 和 d，有 e*d =1(mod Φ(n) )，求出的 d 作为私钥。具体算法如下：
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料