卷积神经网络CNN学习笔记 pdf.pdf-资料库

0b96cd44-797b-4311-8367-5a32fce2a79d.pdf-第1页.png

第1页 / 共7页

0b96cd44-797b-4311-8367-5a32fce2a79d.pdf-第2页.png

第2页 / 共7页

0b96cd44-797b-4311-8367-5a32fce2a79d.pdf-第3页.png

第3页 / 共7页

0b96cd44-797b-4311-8367-5a32fce2a79d.pdf-第4页.png

第4页 / 共7页

0b96cd44-797b-4311-8367-5a32fce2a79d.pdf-第5页.png

第5页 / 共7页

0b96cd44-797b-4311-8367-5a32fce2a79d.pdf-第6页.png

第6页 / 共7页

0b96cd44-797b-4311-8367-5a32fce2a79d.pdf-第7页.png

第7页 / 共7页

CNN学习笔记学习笔记个人整理的CNN学习笔记，所有素材均来自于互联网，版权归作者所有，感谢各位作者的无私分享。我个人仅作了整理便于学习之用。 http://www.cnblogs.com/charleshuang/p/3651843.html http://www.68idc.cn/help/buildlang/ask/20150705417730.html（CNN的背景介绍） http://www.68idc.cn/help/mobilesys/other/20160516616446.html（全面的综合讲解）先解释一下：什么是卷积？先解释一下：什么是卷积？翻转和平移的重叠部分的面积。在泛函分析中，卷积、旋积或摺积(英语：Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子，表征函数f 与 g经过翻转和平移如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“滑动平均卷积的基本内涵公式：滑动平均”的推广。设:f(x),g(x)是R1上的两个可积函数，作积分：上面公式继而解释为： 1.如果卷积的变量是序列x(n)和h(n)，则卷积的结果： 2.如果卷积的变量是函数x(t)和h(t)，则卷积的计算变为：物理意义：加权叠加加权叠加图示见这个网址： http://www.zhihu.com/question/22298352?rf=21686447 1. 2. 3.x[n]乘以y[n]的过程（1）x[n]乘以y[0]并平移到位置0：（2）x[n]乘以y[1]并平移到位置1：（3）x[n]乘以y[2]并平移到位置2：（4）最后把上面三个图叠加，就得到了x[n]乘以y[n]：重复一遍，这就是卷积的意义：加权叠加。重复一遍，这就是卷积的意义：加权叠加。 1.概述概述 CNN有两点：非全连接、权重共享非全连接非全连接：并不是所有上、下层的神经元都直接相连权重共享权重共享：同一层中某些神经元之间的连接权重是共享的（即相同的），降低了复杂度。 2.CNN结构结构特征提取：提取局部特征局部特征。一旦一个特征被提取出来，只要它相对于其他特征的位置被近似地保留下来，它的精确位置就变得没有那么重要了。特征映射：网络的每一个计算层都是由多个特征映射组成多个特征映射组成的，每个特征映射都是平面形式的。平面中单独的神经元在约束共享相同的突触权值集，这种结构形式具有如下的有益效果：a.平移不变性。b.自由参数数量的缩减(通过权值共享实下共享相同的突触权值集现)。子抽样：每个卷积层跟着一个实现局部平均和子抽样的计算层，由此特征映射的分辨率降低。这种操作具有使特征映射的

输出对平移和其他形式的变形的敏感度下降的作用。 2.1 稀疏连接稀疏连接可以看到是局部连接，m层只连接m-1层的3个，而不是5个设第m-1层为视网膜输入层，第m层的接受域的宽度为3，也就是说该层的每个单元与且仅与输入层的3个相邻的神经元相连，第m层与第m+1层具有类似的链接规则 m-1层为视网膜输入层（接受自然图像）。根据上图的描述，在m-1层上面的m层的神经元节点都具有宽度为3的感受野，m 层每一个节点连接下面的视网膜层的3个相邻的节点。多层堆积形成了滤波器（不再是线性的了），它也变得更具有全局性了（如包含了一大片的像素空间）。比如，在上图中，第m+1层能够对宽度为5的非线性特征进行编码（就像素空间而言）。 2.2 权值共享（权值共享（Shared Weights））在CNNs中，每一个稀疏滤波器hi在整个感受野中是重复叠加的，这些重复的节点形式了一种特征图（feature map）,这个特种图可以共享相同的参数，比如相同的权值矩阵和偏置向量。在图中，三个隐层节点属于同一个特征图因为颜色相同，所以权重相同权值为什么要共享？因为1.重复单元在感受野的什么位置，他们都可以检测到特征。（想象一下一只猫在你面前走，特征会随之移动，眼睛都可以检测到）2.减少参数数，降低训练难度，避免过拟合。图示权值共享：除了增加卷积层和采样层，在传统人工神经网络的基础上，卷积神经网络还通过感受野和权值共享大大地减少了参数，降低了训练难度，也避免了参数过多引起过拟合(overfitting)。卷积神经网络的输入是一幅幅的图像，根据传统的人工神经网络，在第2层的每个unit都要和输入层图像的每个像素连接，这里我们假设第2层有1M个hidden units，输入图像大小1000*1000，那么这一层要训练的权值w就是1M 10001000=10^12 个，如下图左：而人们发现人是通过一个局部的感受野去感受图像的，且图像的空间联系是局部的，每一个神经元并不需要对全局图像感受，每个神经元只用感受局部的图像区域，然后在更高层将这些神经元的信息综合起来得到全局信息。这样，我们就可以减少连接数目了，，假设感受野是1010大小，那么第2层的每个unit只用和一个1010的感受野连接，这样的感受野有100100个，那么这一层要训练的权值w是1M1010=10^8个，如上图右。可以看到，通过感受野，隐层的权值个数已经从10^12降到了10^8个，每个hidden unit有1010=100个参数。人们认为对于不同的感受野区域，要提取的特征是相似的，比如边缘，颜色变化等等，这样，我们可以在不同的感受野用同样的方式去感受特征，也就是说，用一个卷积核去卷积全部的感受野。这就是权值共享，就是让这1M个hidden units共享同一组参数(100个权值)，那么隐层权值个数就降到了100个。下图左中的红色，黑色，绿色，蓝色的感受野区域使用相同的参数来做卷积。

下面的分析来源于： http://blog.csdn.net/zouxy09/article/details/8781543 我们知道，隐含层的每一个神经元都连接10x10个图像区域，也就是说每一个神经元存在10x10=100个连接权值参数。那如果我们每个神经元这100个参数是相同的呢？也就是说每个神经元用的是同一个卷积核去卷积图像。这样我们就只有多少个参数？？只有100个参数啊！！！亲！不管你隐层的神经元个数有多少，两层间的连接我只有100个参数啊！亲！这就是权值共享啊！亲！这就是卷积神经网络的主打卖点啊！亲！（有点烦了，呵呵）也许你会问，这样做靠谱吗？为什么可行呢？好了，你就会想，这样提取特征也忒不靠谱吧，这样你只提取了一种特征啊？对了，真聪明，我们需要提取多种特征对不？假如一种滤波器，也就是一种卷积核就是提出图像的一种特征，例如某个方向的边缘。那么我们需要提取不同的特征，怎么办，加多几种滤波器不就行了吗？对了。所以假设我们加到100种滤波器，每种滤波器的参数不一样，表示它提出输入图像的不同特征，例如不同的边缘。这样每种滤波器去卷积图像就得到对图像的不同特征的放映，我们称之为Feature Map。所以100种卷积核就有100个Feature Map。这100个Feature Map就组成了一层神经元。到这个时候明了了吧。我们这一层有多少个参数了？ 100种卷积核x每种卷积核共享100个参数=100x100=10K，也就是1万个参数。才1万个参数啊！亲！（又来了，受不了了！）见上图右：不同的颜色表达不同的滤波器。嘿哟，遗漏一个问题了。刚才说隐层的参数个数和隐层的神经元个数无关，只和滤波器的大小和滤波器种类的多少有关。那么隐层的神经元个数怎么确定呢？它和原图像，也就是输入的大小（神经元个数）、滤波器的大小和滤波器在图像中的滑动步长都有关！例如，我的图像是1000x1000像素，而滤波器大小是10x10，假设滤波器没有重叠，也就是步长为10，这样隐层的神经元个数就是(1000x1000 )/ (10x10)=100x100个神经元了，假设步长是8，也就是卷积核会重叠两个像素，那么……我就不算了，思想懂了就好。注意了，这只是一种滤波器，也就是一个Feature Map的神经元个数哦，如果100个Feature Map就是100倍了。由此可见，图像越大，神经元个数和需要训练的权值参数个数的贫富差距就越大。总之，卷积网络的核心思想是将：局部感受野、权值共享（或者权值复制）以及时间或空间亚采样这三种结构思想结合总之，卷积网络的核心思想是将：局部感受野、权值共享（或者权值复制）以及时间或空间亚采样这三种结构思想结合起来获得了某种程度的位移、尺度、形变不变性。起来获得了某种程度的位移、尺度、形变不变性。 2.3 实例实例视觉皮层存在两类相关的细胞，S细胞（Simple Cell）和C（Complex Cell）细胞。S细胞在自身的感受野内最大限度地对图像中类似边缘模式的刺激做出响应，而C细胞具有更大的感受野，它可以对图像中产生刺激的模式的空间位置进行精准地定位。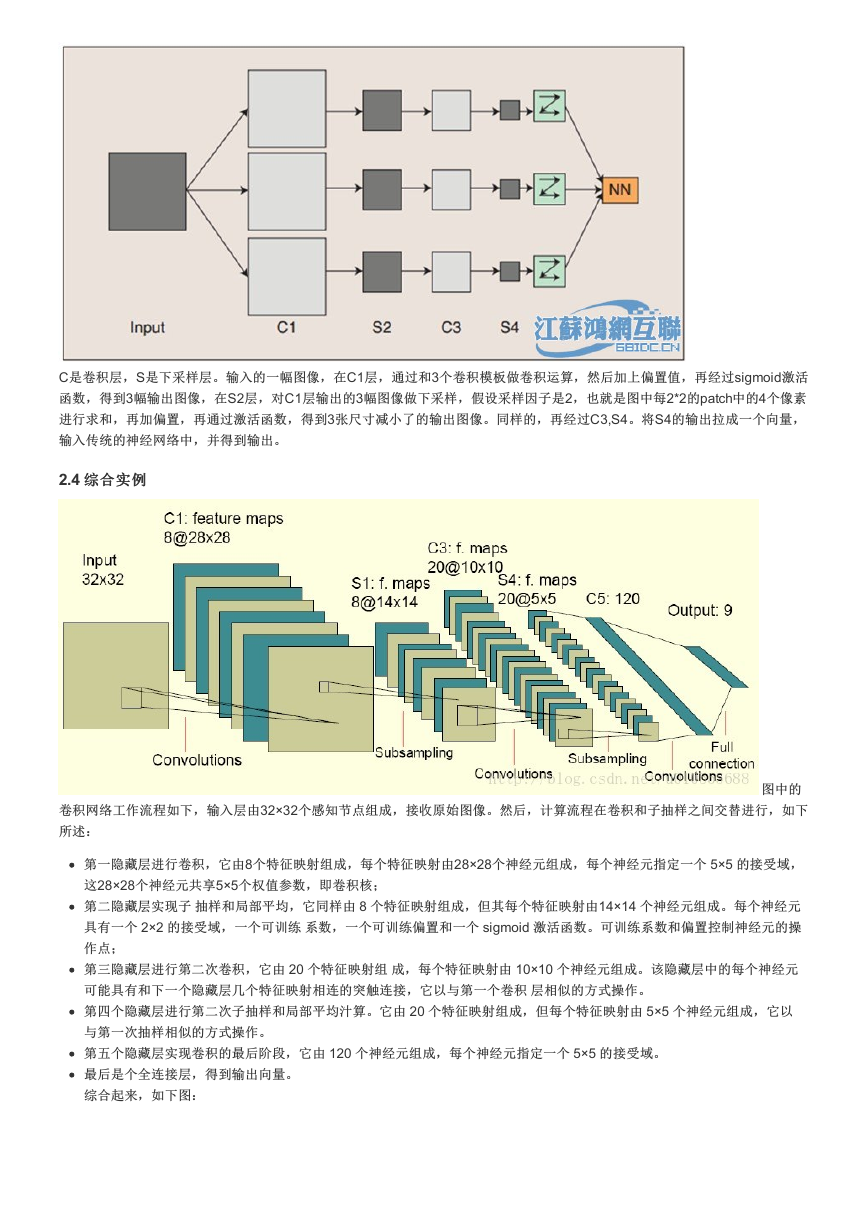 C是卷积层，S是下采样层。参看这个两个网址，对理解CNN非常有帮助： http://www.68idc.cn/help/buildlang/ask/20150705417730.html http://www.68idc.cn/help/buildlang/ask/20150705419299.html

C是卷积层，S是下采样层。输入的一幅图像，在C1层，通过和3个卷积模板做卷积运算，然后加上偏置值，再经过sigmoid激活函数，得到3幅输出图像，在S2层，对C1层输出的3幅图像做下采样，假设采样因子是2，也就是图中每2*2的patch中的4个像素进行求和，再加偏置，再通过激活函数，得到3张尺寸减小了的输出图像。同样的，再经过C3,S4。将S4的输出拉成一个向量，输入传统的神经网络中，并得到输出。 2.4 综合实例综合实例图中的卷积网络工作流程如下，输入层由32×32个感知节点组成，接收原始图像。然后，计算流程在卷积和子抽样之间交替进行，如下所述：第一隐藏层进行卷积，它由8个特征映射组成，每个特征映射由28×28个神经元组成，每个神经元指定一个 5×5 的接受域，这28×28个神经元共享5×5个权值参数，即卷积核；第二隐藏层实现子抽样和局部平均，它同样由 8 个特征映射组成，但其每个特征映射由14×14 个神经元组成。每个神经元具有一个 2×2 的接受域，一个可训练系数，一个可训练偏置和一个 sigmoid 激活函数。可训练系数和偏置控制神经元的操作点；第三隐藏层进行第二次卷积，它由 20 个特征映射组成，每个特征映射由 10×10 个神经元组成。该隐藏层中的每个神经元可能具有和下一个隐藏层几个特征映射相连的突触连接，它以与第一个卷积层相似的方式操作。第四个隐藏层进行第二次子抽样和局部平均汁算。它由 20 个特征映射组成，但每个特征映射由 5×5 个神经元组成，它以与第一次抽样相似的方式操作。第五个隐藏层实现卷积的最后阶段，它由 120 个神经元组成，每个神经元指定一个 5×5 的接受域。最后是个全连接层，得到输出向量。综合起来，如下图：

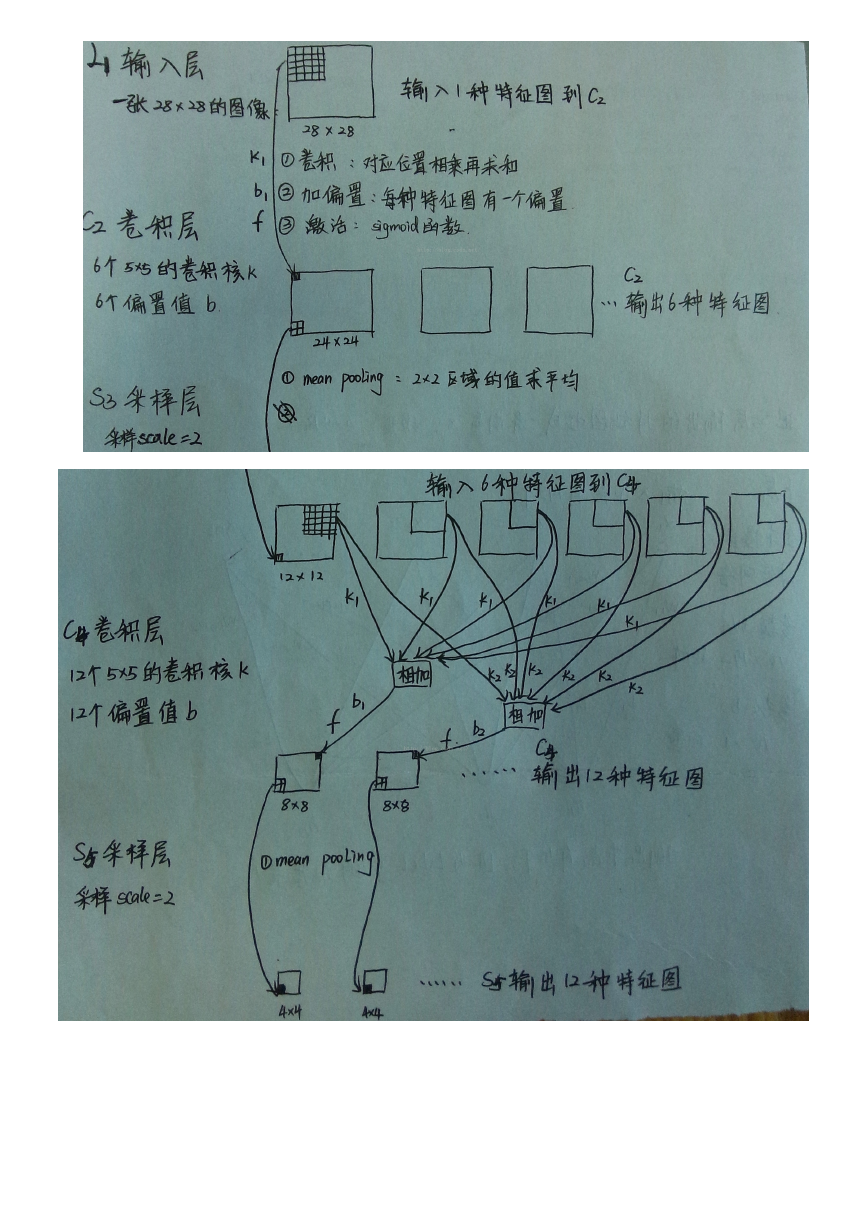
上图中28如何变成24的？ 12如何变成8的？详情见这个网址：http://ufldl.stanford.edu/wiki/index.php/Featureextractionusing_convolution 这个过程中，有这么几个参数： * a. 深度depth：神经元个数，决定输出的depth厚度。同时代表滤波器个数。 * b. 步长stride：决定滑动多少步可以到边缘。 * c. 填充值zero-padding：在外围边缘补充若干圈0，方便从初始位置以步长为单位可以刚好滑倒末尾位置，通俗地讲就是为了总长能被步长整除。最左边一列是输入层，第二列是第一个滤波器（W0），第三列是第二个滤波器（W1），第四列是输出层。 * 该图有两个神经元，即depth=2，意味着有两个滤波器。 * 数据窗口每次移动两个步长取3*3的局部数据，即stride=2。 * zero-padding=1。 3.CNN的激励层与池化层的激励层与池化层 ReLU激励层

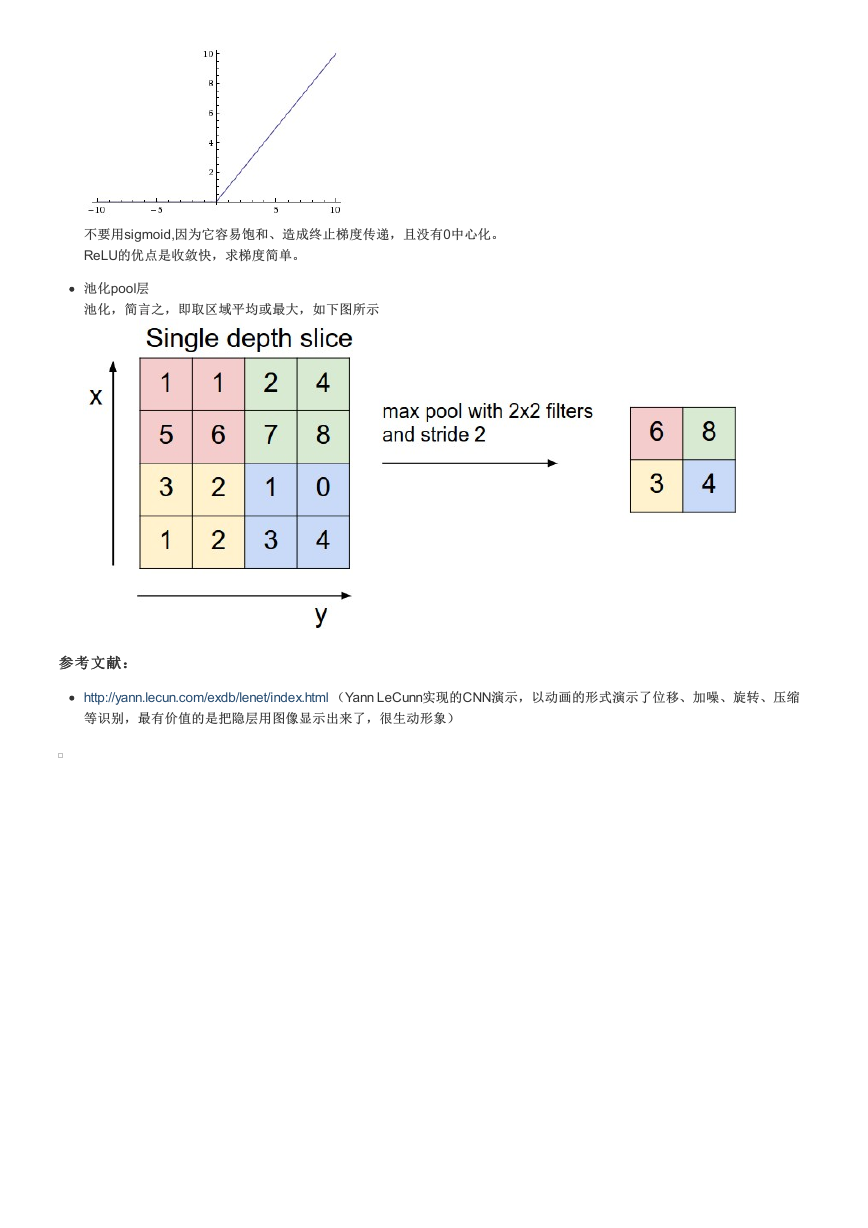
不要用sigmoid,因为它容易饱和、造成终止梯度传递，且没有0中心化。 ReLU的优点是收敛快，求梯度简单。池化pool层池化，简言之，即取区域平均或最大，如下图所示参考文献：参考文献： http://yann.lecun.com/exdb/lenet/index.html （Yann LeCunn实现的CNN演示，以动画的形式演示了位移、加噪、旋转、压缩等识别，最有价值的是把隐层用图像显示出来了，很生动形象）

资料库

卷积神经网络CNN学习笔记 pdf.pdf

相关推荐

课程资源

热门标签

最新资料