一、实验目的 通过同学自己用 MATLAB 等软件编程计算电磁场问题，使学生掌握电磁场数 值计算的基本思想和方法，掌握 MATLAB 等软件编程技巧，学会用 MATLAB 等 软件应用于有限差分法的数值解。 二、实验内容 一个二维静电场，电位函数为  yx, ，边界条件如题 4.29 图所示，将正方 形场域分成 20 个正方形网格。有 16 个内部网格点。假定 16 个网格点的初 始 值 都 定 为 零 ， 试 用 超 松 弛 法 确 定 16 个 内 网 格 点 的 电 位 值 。  设所有内节点的相邻两次迭代值之间的误差不超过 10-5，根据超松弛法公式 u2(i,j)=u1(i,j)+(u1(i,j+1)+u1(i+1,j)+u2(i-1,j)+u2(i,j-1)-4*u1(i,j) )*a/4 计算出各内网格点的电位值。本实验使用 MATLAB 进行仿真。 三、实验程序 %设置网格节点数 6*6=36 个 %设置行列二位数组 >> x=6;y=6; u1=ones(y,x); m=5;n=5; u1(y,:)=ones(1,x)*50; u1(1,:)=ones(1,x)*100; for i=1:y %横纵向网格数 u1(i,1)=0; u1(i,x)=100; %上下两行条件边界值 %左右两列条件边界值 end t1=(cos(pi/m)+cos(pi/n))/2; a=2/(1+sqrt(1-t1*t1)); u2=u1; w=1; t=0; k=0; %初始化 while(w>1e-5) %计算迭代次数 k=k+1 w=0; %计算松弛因子 a %由 u1 迭代，算出 u2，迭代精度 w 为 10-5 

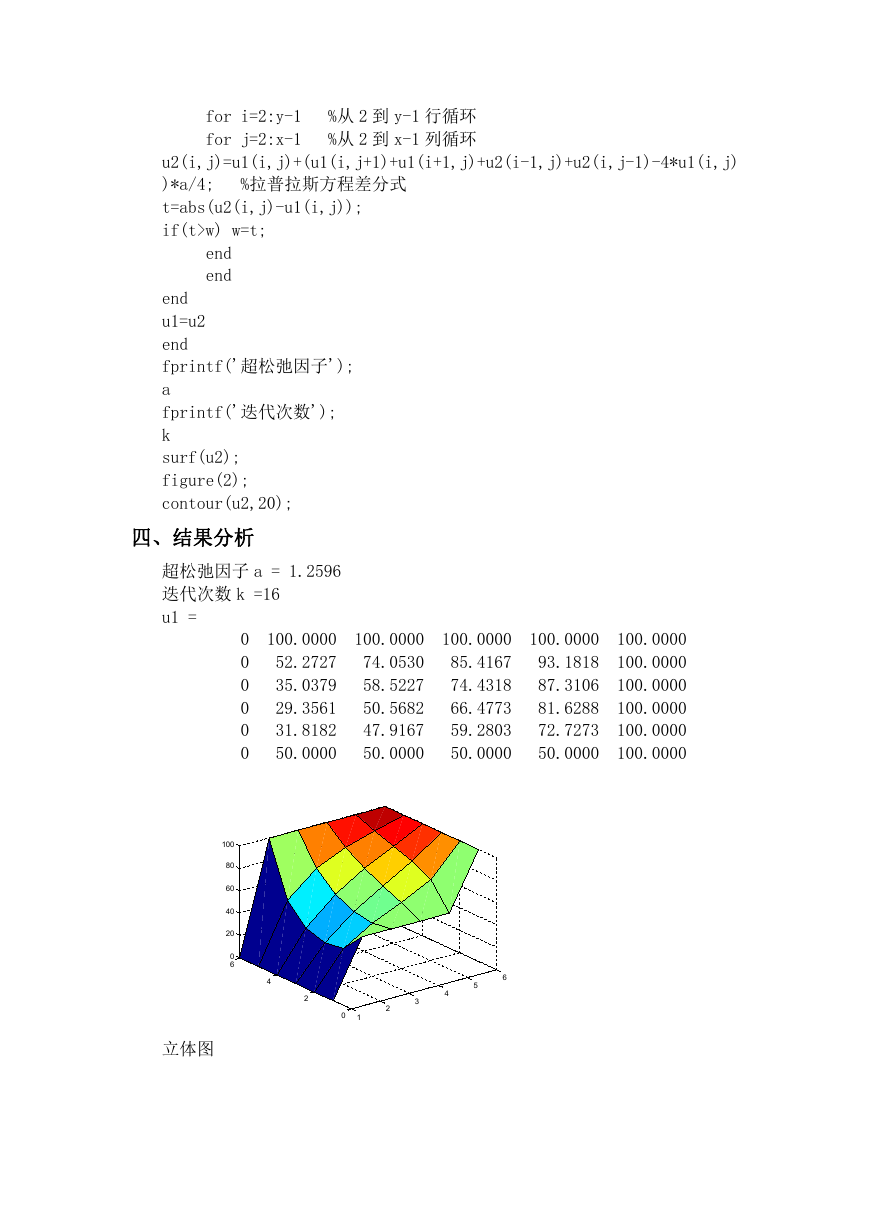
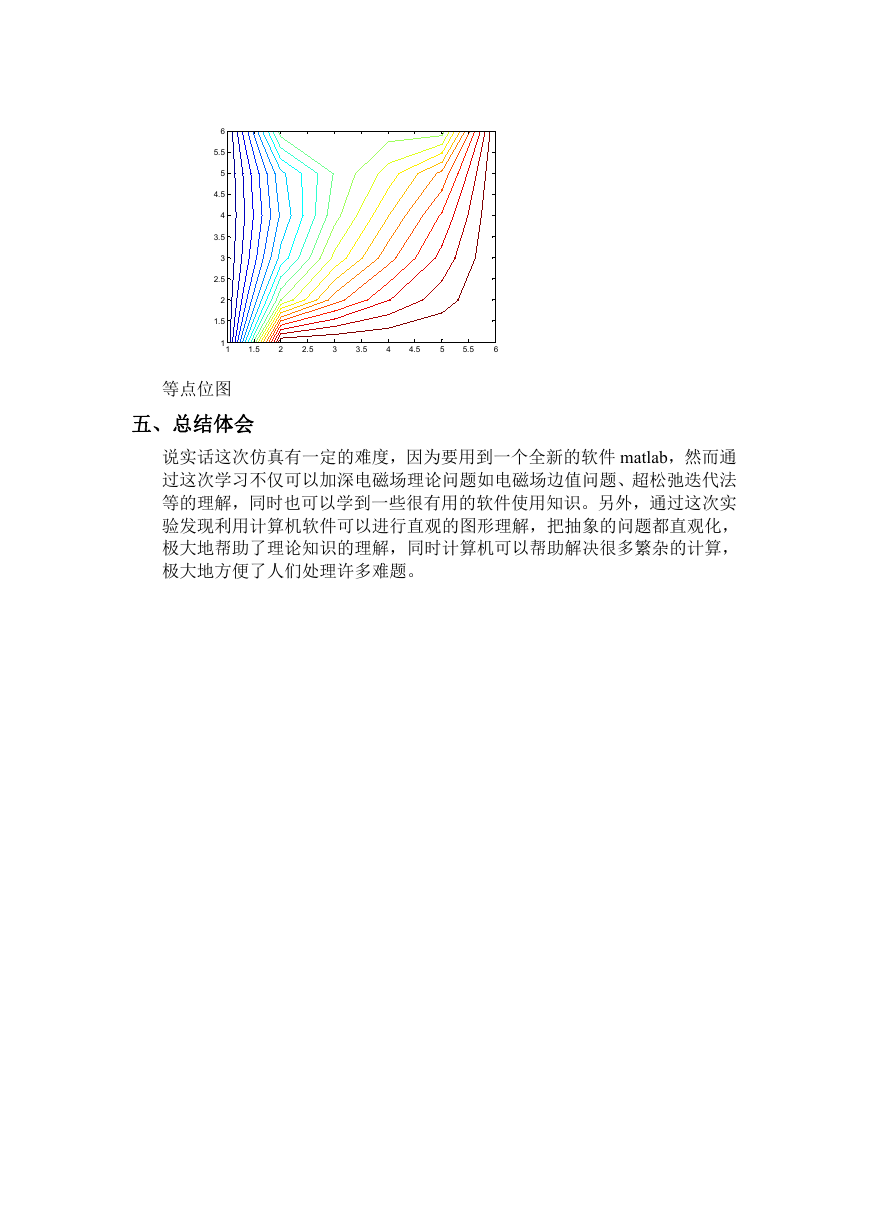
for i=2:y-1 for j=2:x-1 %从 2 到 y-1 行循环 %从 2 到 x-1 列循环 u2(i,j)=u1(i,j)+(u1(i,j+1)+u1(i+1,j)+u2(i-1,j)+u2(i,j-1)-4*u1(i,j) )*a/4; t=abs(u2(i,j)-u1(i,j)); if(t>w) w=t; %拉普拉斯方程差分式 end end end u1=u2 end fprintf('超松弛因子'); a fprintf('迭代次数'); k surf(u2); figure(2); contour(u2,20); 四、结果分析 超松弛因子 a = 1.2596 迭代次数 k =16 u1 = 0 0 0 0 0 0 100.0000 52.2727 35.0379 29.3561 31.8182 50.0000 100.0000 74.0530 58.5227 50.5682 47.9167 50.0000 100.0000 85.4167 74.4318 66.4773 59.2803 50.0000 100.0000 93.1818 87.3106 81.6288 72.7273 50.0000 100.0000 100.0000 100.0000 100.0000 100.0000 100.0000 100 80 60 40 20 0 6 立体图 4 2 3 2 0 1 6 5 4 

6 5.5 5 4.5 4 3.5 3 2.5 2 1.5 1 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 等点位图 五、总结体会 说实话这次仿真有一定的难度，因为要用到一个全新的软件 matlab，然而通 过这次学习不仅可以加深电磁场理论问题如电磁场边值问题、超松弛迭代法 等的理解，同时也可以学到一些很有用的软件使用知识。另外，通过这次实 验发现利用计算机软件可以进行直观的图形理解，把抽象的问题都直观化， 极大地帮助了理论知识的理解，同时计算机可以帮助解决很多繁杂的计算， 极大地方便了人们处理许多难题。