第1页 / 共16页
第2页 / 共16页
第3页 / 共16页
第4页 / 共16页
第5页 / 共16页
第6页 / 共16页
第7页 / 共16页
第8页 / 共16页
数值计算课后习题答案.doc
实用数值计算方法习题参考答案
1．1 因为
dx
k
x
k
x
*
k
故
第一章 引 论
(
，（k=1，2，…，n），所以
x
)
k
y
*
y
)(
y
n
k
1
f
x
k
x
k
x
*
k
f
n
x
1
k
k
(
x
k
)
S
1．2 由于矩形面积
1.0
d
而
)(
sE
dl
。所以，面积的绝对误差限和相对误差限分别可以估计为
S
S
，利用全微分近似有
l
dl
,2.0
110
1.0
2.0
27
80
。
d
l
l
dl
S
S
d
27
110
80
)(
sEr
.0
0031
%31.0
1．3 由于相对误差满足：
)(
xE
有
3
10
.0
125
10
3
3
10
%1.0
1
8
1
2
a
1
1
n
10
，而
20
.4
4721
。由 a1= 4，取 n=4 时，
1．4 由 Taylor 中值定理
x
sin
1
!3
x
1
!5
而
S
x
R
1． 6
1
!3
3
x
1
!5
5
x
1
!7
7
x
cos
，（介于 0 和 x 之间）
5
x
，所以截断误差限为
S
sin
x
X1
0.1
X2
0.3
x
7
x
1
cos
1
!7
5040
5 七个零件的标定值
X3
0.1
X4
0.1
X5
1.5
7
.1
9841
x
7
4
10
X6
16
X7
0.7488
不同等级的零件参数取值范围如下：
下限
0.0990
0.2970
0.0990
0.0990
x1
X2
X3
X4
A 等零件相对误差不超过 1%
下限
1.4850
15.8400
0.7413
X5
X6
X7
上限
0.1010
0.3030
0.1010
0.1010
上限
1.5150
16.1600
0.7562
1
下限
0.0950
0.2850
0.0950
0.0950
下限
0.0900
0.2700
0.0900
0.0900
X1
X2
X3
X4
X1
X2
X3
X4
B 等零件相对误差不超过 5%
下限
1.4250
15.2000
0.7113
X5
X6
X7
上限
0.1050
0.3150
0.1050
0.1050
上限
1.5750
16.8000
0.7862
C 等零件相对误差不超过 10%
上限
0.1100
0.3300
0.1100
0.1100
下限
1.3500
14.4000
0.6739
上限
1.6500
17.6000
0.8236
X5
X6
X7
1.7 算法如下：
(1).将 100 个小数按由小到大排序
(2).将排序后的 100 个小数依次相加
(3).将 100 个小数相加结果与 1012 相加
(4).输出计算结果，结束。
1． 8 一个八位二进制数为 (10111101)2
（1）用秦九韶算法将其转化为 10 进制数只需六次乘法
189
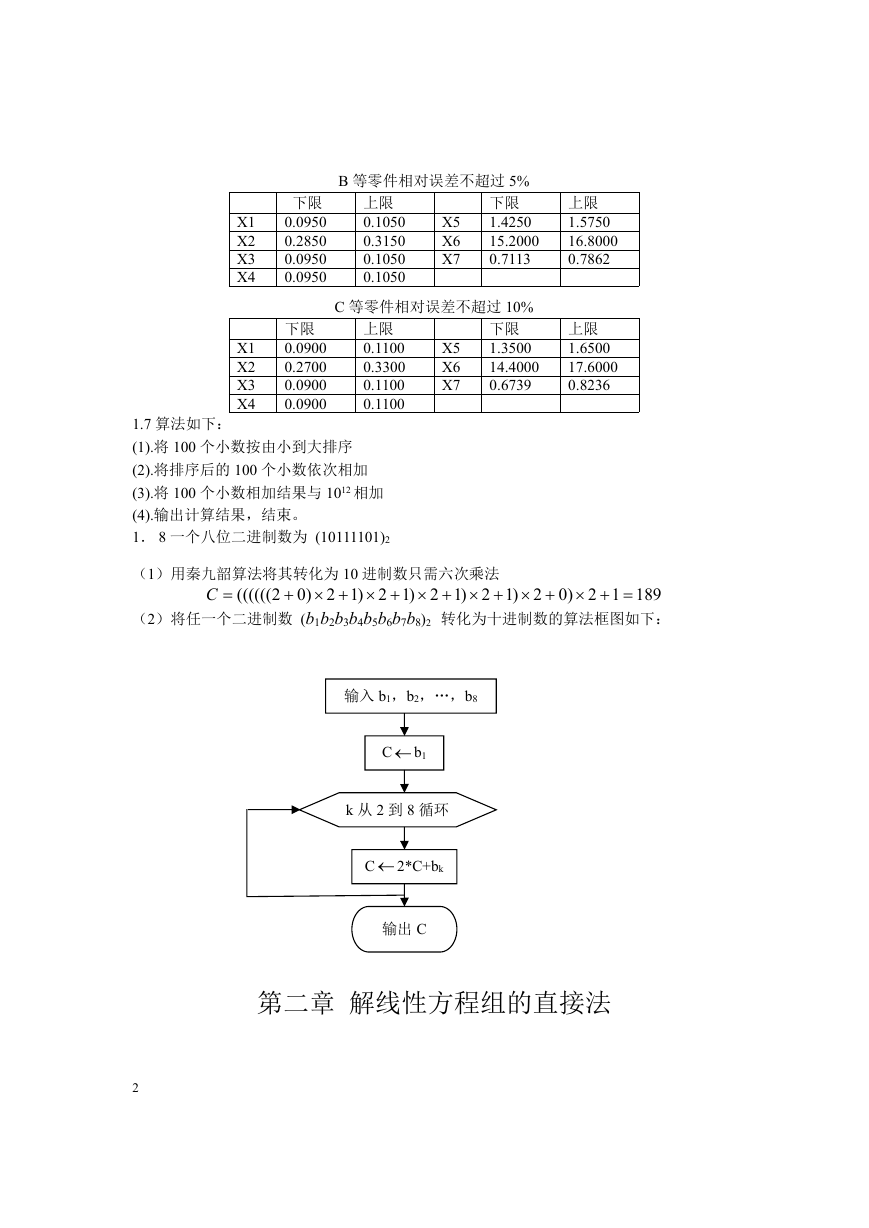
（2）将任一个二进制数 (b1b2b3b4b5b6b7b8)2 转化为十进制数的算法框图如下：
12)02)12)12)12)12)02
C
((((((
输入 b1，b2，…，b8
C b1
k 从 2 到 8 循环
C 2*C+bk
输出 C
第二章 解线性方程组的直接法
2
2，1
x1 = 1
为
x1 = 2
x1 = 3 。m21 = 1，m31 = 2，m32 = -2。消元过程所得增广矩阵
B
11
20
00
1
3
7
6
5
21
996
.5
x
1
.2
0028
5625
4
x
x
2
.2
002
x
x
3705
.0
x
2
3
3
3
4178
.7
.0
4037
3516
.0
2． 2
.3
2．3 令
L
1
1
m
m
m
1
1
21
31
41
则，由矩阵乘法得
1
m
m
m
21
31
41
1
1
而
1
L
1
所以
显然，有
1
1
，
L
2
1
1
m
m
32
42
1
1
L3 L2 L1 A = U
，
1
L
2
1
1
m
m
32
42
1
1
，
L
3
1
1
1
m
43
1
，
1
L
3
1
1
1
m
43
1
。
。
ULLLA
1
1
1
3
2
1
1
1
LLL
1
3
2
1
1
m
m
m
21
31
41
U
1
m
43
1
1
m
m
32
42
2．5 当 n=2 时，由于
ca
12
件的 n-1 阶三对角矩阵行列式不为零。现考虑 n 阶三对角矩阵的情形。
b ，显然，
2
b ，
1
bb
21
A
2
c
1
a
2
0
。假设满足条
3
A
n
根据行列式性质，将第 n 列乘
2
2
2
c
b
1
a
c
1
b
a 加到第(n-1)列，然后按第 n 行展开行列式，得
b
b
1
n
a
1
n
b
a
c
1
n
n
n
n
n
b
1
a
2
A
n
b
n
c
c
1
b
2
~
b
n
a
1
2
n
1
由于右边行列式是 n-1 阶三对角矩阵行列式，现在只须证明 n-1 阶三对角矩阵的元素满足
题目所给条件，则由数学归纳法可得 n 阶三对角矩阵行列式不为零。证明如下
由于
b ，
n
a
n
b
n
1
a
n
1
c
n
1
，所以有
~
b
n
1
b
n
1
a
b
n
n
c
n
1
b
n
1
a
b
n
n
a
b
n
n
1
，
b
n
1
c
n
1
a
n
1
。而
c
n
1
b
n
1
c
n
1
a
n
1
所以，n-1 阶三对角矩阵的元素满足题目所给条件（主对角占优）。
第三章 插值方法
3．1 整理已有数据构造函数表
X
f(x)
1
793
31
861
61
880
令 h = 30，由拉格朗日插值基函数求导数,得
2
x
)
2
l
0
x
x
2
)(
x
(
x
1
2
2
h
( )
代入二次插值函数 L x
2
(
x
1
2
x
2
*
)(
,
xl
1
( )
( )
l x y
l x y
1
0
1
)
(2
x
x
yx
2
1
2
y
y
1
0
0
0
)
0
x
2
0
2
( )
x y
(
x
1
(
x
h
l
2
y
1
y
2
,)
2
x
l
2
)(
x
，并令
2
x
y
)
0
2
xL
)(2
=57.6327
)
x
1
(
x
0
2
2
h
0
，求解得
所以，从 5 月 1 日到 6 月 30 日这些天中，可以认为 6 月 27 日这一天日照时间最长。
3．2 构造函数表
4
猪肉产量 X
猪肉价格 Y
28
6.8
27.28
7.09
27.02
7.19
如果 1999 年猪肉产量为 27.5 万吨，则由二次拉格朗日插值函数
y
)5.27(
)5.27(
)5.27(
)5.27(
l
y
1
l
1
2
.7
0034
2
L
y
0
推测 1999 年猪肉价格为：7.00（元）。
3．3 确定函数如下：
l
0
2
y
,80
x
,8
0
x
100
x
100
由于
y
100(
8)
，所以一个新手需要织 100 匹布以后才能成为一名技术熟练的纺织女工。
3.4 (1) 取 f(x)=1，则 f (n)(x) = 0 (n > 0)。以 f(x)为被插值函数，它的 n 次拉格朗日插值函数
为
Ln(x) = l0(x)f(x0)+ l1(x) f(x1) +……+ ln(x) f(xn) = l0(x) + l1(x) +……+ ln(x)
由插值误差余项公式，知插值误差为零。所以
Ln(x) = f(x) = 1
即：l0(x) + l1(x) +……+ ln(x)=1。
(2) 取 f(x)= xk
次拉格朗日插值函数为
(k =1，2，……，n)，则 f (n)(x) = 0 (n > 0)。以 f(x)为被插值函数，它的 n
Ln(x) = l0(x)f(x0)+ l1(x) f(x1) +……+ ln(x) f(xn)
= l0(x)x0k + l1(x)x1k +……+ ln(x)xnk
由插值误差余项公式，知插值误差为零。所以
即：l0(x)x0k + l1(x)x1k +……+ ln(x)xnk=xk。
Ln(x) = f(x) = xk
(k =1，2，……，n)
3．5
*
x
(
x
1
2
2
(
2
x
2
x
1
2
)
y
0
)
yx
1
(
0
x
2
(
x
2
2
2
)
y
x
1
0
(
)
yx
1
0
2
(
x
1
x
1
2
x
0
)
yx
0
2
)
y
2
3．6 设 f(x，y)是被插值函数，z(x，y)=ax+by+c 为插值函数。
（1）由插值条件 z(x1，y1)=u1，z(x2，y2)=u2，z(x3，y3)=u3。得
u
1
u
u
ax
1
ax
2
ax
by
1
by
by
1
1
1
u
1
u
u
y
1
y
y
x
1
x
x
a
b
c
c
c
c
或
3
3
2
3
2
3
2
3
2
3
2
（2）二元线性插值函数存在唯一的条件为
x
1
x
x
2
3
y
1
y
y
2
3
1
1
1
0
，根据行列式的几何意义可
5
知，要求三个插值结点所形成的三角形面积不为零。即三点不共线。
（3）设
,(
yxz
)
,(
)
uyxl
1
1
l
2
)
,(
uyx
2
)
uyxl
3
,(
3
，三个线性插值基函数为
,(
yxl
1
)
ybxa
1
1
c
1
，
l
2
,(
yx
)
ybxa
2
2
c
2
，
yxl
3
,(
)
ybxa
3
3
c
3
它们应满足的插值条件见下表
（x, y）
l 1(x, y)
l 2(x, y)
l 3(x, y)
则由插值条件列出线性方程组
1
0
0
c
1
c
1
c
1
xa
11
xa
21
xa
31
yb
11
yb
1
yb
1
2
3
分别求解三个线性方程组可得
，
(x1, y1)
1
0
0
(x2, y2)
0
1
0
(x3, y3)
0
0
1
xa
12
xa
2
xa
2
3
2
yb
1
2
yb
2
yb
2
3
2
c
2
c
c
2
2
0
1
0
，
xa
13
xa
3
xa
33
2
yb
1
3
yb
3
yb
3
3
2
c
3
c
c
3
3
0
0
1
2
x
x
x
3
x
1
x
x
2
3
0
,(
yxl
1
)
3．7 （1）
1
(1
(1
(1
A
x
1
x
x
2
3
2
3
y
y
y
y
1
y
y
2
3
1
1
1
1
1
1
，
l
2
,(
yx
)
x
1
x
x
3
x
1
x
x
2
3
y
2
y
y
3
y
1
y
y
2
3
1
1
1
1
1
1
，
yxl
3
,(
)
x
1
x
2
x
x
1
x
x
2
3
0
0
)(
)(
)
)
)
(
(
x
x
2
3
x
x
0
0
0
0
0
)(
0
x
x
2
3
x
1
x
1
)
)
(
x
3
x
x
3
x
1
)(
x
3
x
2
)
x
0
x
x
0
0
（2）
A
001
010
100
000
0
0
0
1
所以，
a
0
( 0
xf
)
，
a
1
,
[
xxf
1
0
]
，
a
2
6
0
)
(
xf
0
[
]
,
xxf
1
[
,
,
xxxf
1
[
,
,
xxxf
0
1
0
2
2
]
,
x
]
3
[
,
xxxf
,
1
0
]
2
，
a
3
[
,
xxxf
,
1
0
y
1
y
2
y
y
1
y
y
2
3
1
1
1
1
1
1
。
(
xf
0
(
xf
1
(
xf
(
xf
3
)
)
)
2
)
,
x
3
]
2
。
第四章 数据拟合方法
4．1 超定方程组的矩阵形式为
将方程两端同乘以系数矩阵的转置矩阵，可得正规方程组
4
5
2
2
11
3
6
14
2
3
1
4
x
y
30
3
解之，得 x = 2.9774，y = 1.2259。
4．2
3
49
x
y
93
69
时间 t
距离 S
0
0
0.9
10
1.9
30
3.0
50
3.9
80
5.0
110
设物体运动的初速度和加速度分别为 v0 和 a，初始时刻距离为 0，则距离函数为
用后 5 个点的数据作曲线拟合
)(
tS
tv
0
1
2
2
at
t
S
0.9
10
可得，v0 = 10.6576，a = 4.6269
Bx
4．3 令
ln
ln
，则
A
y
z
z
1.9
30
3.0
50
3.9
80
5.0
110
。处理数据如下
x
z = ln y
1
4.0943
2
3.4012
3
2.9957
4
2.7081
由最小二乘法作线性拟合得，ln A = 4.4409，B = -0.4564。所以 A =84.8528。故，所求经
难公式为
y
25.84
e
.0
4564
x
。
第五章 数值积分方法
5．1 椭圆周长公式为：
L
2/
4
a
0
1
e
2 cos
2
t
dt
由于
1
11
2
x
x
，所以被积函数
7
积分，得
L
4
a
5．2
（1）令
)(1
xF
x
a
利用泰勒中值定理
f
)(
t
1
e
2
2
cos
t
11
2
2
e
2
cos
t
2/
11(
2
2
e
2
cos
t
)
dt
[4
a
2
1
2
2
e
]
4
2
a
1(
2
e
4
)
0
f
)(
t
dt
，则
)(1
aF
0
，
)('1
xF
)(
xf
，
)(''1
x
F
f
)('
x
)(
bF
1
)(
aF
1
(
)('
aFab
)
1
2
)
(
Fab
)(''
2
1
所以，有
（2）令
)(2
xF
b
x
利用泰勒中值定理
所以，有
xfb
)(
a
dx
)(
(
afab
)
2
)
(
ab
2
)('
f
f
)(
t
dt
，则
)(2
bF
0
，
)('2
xF
)(
xf
，
)(''2
F
x
f
)('
x
)(
aF
2
)(
bF
2
(
)('
bFba
)
2
(
2
)
Fba
)(''
2
2
xfb
)(
a
dx
)(
(
bfab
)
2
)
(
ab
2
)('
f
（3）由泰勒中值定理
)(
xf
baf
(
2
)
(
x
fba
)
2
('
ba
2
)
1
2
(
x
ba
2
2
)
)(''
f
积分，可得
b
a
)(
xf
dx
bafab
(
2
)
(
)
1
2
b
a
(
x
ba
2
2
)
f
)(''
dx
由积分第二中值定理，可得
b
a
(
x
xfb
)(
a
ba
2
dx
2
dx
)(''
)
f
bafab
(
2
(
)
故，
8
2
)
dx
1
12
f
(''
)(
ab
3
)
f
)(''
f
)
ba
2
3)
(
ab
b
(
x
a
)(''
24
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
