2 2 第 26卷 　第 3期 2005年 9月 太 原 科 技 大 学 学 报 JOURNAL OF TA IYUAN UN IVERSITY OF SC IENCE AND TECHNOLOGY Vol. 26　No. 3 Sep. 2005 文章编号 : 1673 - 2057 (2005) 03 - 0172 - 04 曲柄滑块机构的 MATLAB仿真 陈德为 (福州大学机械工程及自动化学院 ,福州 350002) 　　摘 　要 :研究了基于 MATLAB ( Simulink)的曲柄滑块机构仿真 。内容包括曲柄滑块 机构中连杆的角速度仿真 ,滑块的位移 、速度以及加速度仿真 。 　　关键词 :曲柄滑块机构 ; MATLAB ( Simulink)仿真 中图分类号 : TH13　　文献标识码 : A 　　曲柄滑块机构是单缸四冲程发动机的关键机 构 。对曲柄滑块机构进行运动学仿真意义重大 ,通 过仿真可以揭示曲柄滑块机构连杆 、滑块的运动规 律 。文献 [ 1 ]运用平面曲柄滑块机构函数综合的混 沌方法编写了 MATLAB程序 ,对平面曲柄滑块机构 的函数综合问题进行研究 ,得出了 Jocobi矩阵的通 用表达式 ,找到了实现最大精确点时该问题的全部 解 ,为实际的平面曲柄滑块机构的设计提供了多种 选择方案 ;文献 [ 2 ]在对饲草压捆机压缩机构进行 动态仿真的同时 ,研究了压缩机构内部的曲柄滑块 机构 ;文献 [ 3 ]应用 MATLAB ( Simulink)软件对人造 板工业中多层热压机的重要装置之一的杠杆式同 时闭合机构进行了研究 ,对该机构外框部分以滑块 为主动件的曲柄滑块机构进行了运动学仿真 ;文献 [ 4 ]应用 MATLAB 对自动售货机的送出机构进行优 化设计 。本文以 MATLAB 和 Simulink为研究平台 , 在系统地建立曲柄滑块机构数学模型的基础上 ,进 行了计算机仿真 。主要研究曲柄以匀角速度和匀 角加速度旋转两种情况下 ,曲柄滑块机构中连杆的 旋转角速度的变化规律以及滑块的位移 、速度 、加 速度的变化规律 。仿真结果应用曲线的形式形象 地表达曲柄滑块机构各部位的运动规律 。 1　1曲柄滑块机构运动学方程 [ 5 ] 1 1　曲柄滑块机构的机构组成 曲柄滑块机构的向量图如图 1所示 。曲柄 l1的 长度为 l1 ( l1 = 30mm ) ,旋转角位移为 θ1 ,旋转角速 度为 ω1 ,旋转角加速度为 α1;连杆 l2 的长度为 l2 ( l2 = 120mm ) ,旋转角位移为 θ2 , 旋转角速度为 ω2;滑 块 m 的位移量为 0,速度为 l0 ,加速度为 l 0。 . . 图 1　曲柄滑块机构的向量图 F ig. 1 The vector chart of brace slip block organ iza tion 2　曲柄滑块机构的速度方程 1 根据曲柄滑块机构的向量图 ,把曲柄滑块机构 的向量按 x和 y坐标轴方向分解可以得出 : 收稿日期 : 2005 作者简介 :陈德为 (1962 - 09 01 ) ,男 ,副教授 ,在职博士生 ,研究领域 :机电控制 。 

第 26卷第 3期 　　　　　　　　陈德为 :曲柄滑块机构的 MATLAB仿真 371 l1 co sθ1 + 2co sθ2 = 0 l1 sinθ1 + 2 sinθ2 = 0 式 (1) 、(2)对时间求导 ,并注意到 ω2得 : θ1 =ω1 和 - l1ω1 sinθ1 - 2ω2 sinθ2 = l0 l1ω1 co sθ1 + 2ω2 co sθ2 = 0 写成如下矩阵的形式得 : ω2 1 l2 sinθ2 l2 co sθ2 - 0 l0 = - l1ω1 sinθ1 l1 co sθ1 这就是曲柄滑块机构的速度方程 。 1 3　曲柄滑块机构的加速度方程 (1) (2) θ2 = (3) (4) (5) θ1 = 　　曲柄连杆机构曲柄以 ω1 = 188. 5 rad / s作匀角 速度运动 (这是除草机单缸发动机的正常工作速 度 ) ,主要研究在这一输入作用下的曲柄连杆机构 连杆的运动角速度变化规律以及滑块的位移 、速度 的变化规律 。应用 MATLAB 算法建立计算曲柄滑 块机构的速度方程 ( 5)的 MATLAB 函数模块 slip d l0 block_speed (该模块 in: ω1、θ1、θ2 ; out: ω2、 d t ) 。应 用该 MATLAB Function模块建立了 Simulink仿真模 型如图 2所示 。仿真初始条件 : θ1 = 0 rad、θ2 = 0 rad、l0 = 150 mm (仿真模型符号对应 : alpha1 - α1 ; om ega1 - ω1 ; om ega_2 - ω2 ; theta1 - θ1 ; theta2 - θ2 ; 以下同 ) 。 式 (3) 、( 4)对时间再次求导 ,并注意到 : θ= ω2 和 ω2 =α2得 : ω1 =α1、 ω1、 - l1α1 sinθ1 - l1ω2 1 cosθ1 - l2α2 sinθ2 + - l2ω2 2 cosθ2 = l0 l2ω2 (6) 2 sinθ2 = 0 (7) l1α1 co sθ1 - l1ω2 1 sinθ1 + l2α2 co sθ2 + - 写成如下矩阵形式得 : l2 sinθ2 l2 co sθ2 - 1 0 α2 . . l 0 = - ( l1α1 sinθ1 + l1ω2 l1α1 co sθ1 l1ω2 1 co sθ1 + l2ω2 1 sinθ1 l2ω2 这就是曲柄滑块机构的加速度方程 。 - - 2 co sθ2 ) 2 sinθ2 (8) 2　曲柄滑块机构的匀角速度运动学仿 真 [ 6 - 9 ] 1　匀角速度输入时曲柄滑块机构的 Simulink仿 2 真模型 图 2　曲柄匀角速运动时 S im ulink仿真模型 F ig. 2 S im ulink sim ula tion m odel of the brace hom ogeneous angle speed sport 2　匀角速度输入时曲柄滑块机构的 Simulink仿 2 真曲线分析 　　曲柄连杆机构的曲柄以 ω1 = 188. 5 rad / s作匀 角速度运动时 (对应图 2的仿真模型 ) , 连杆的运动 角速度 ω2 (om ega_2) 的仿真曲线如图 3 ( a) 所示 。 滑块 m 的位移仿真曲线如图 3 ( b) 所示 ,速度仿真 曲线如图 3 ( c) 所示 。 ( a) ( b) ( c) 图 3　匀角速度运动时曲柄连杆机构的 S im ulink仿真曲线 F ig. 3 Brace b ind iny m echan ism sim ulink sim ula tion curve of the hom ogeneus angle speed sport 

471 　　　　　太 原 科 技 大 学 学 报 　　 　　　　　　　　　2005年 　　从仿真曲线可以看出 ,当曲柄以 ω1 = 188. 5 rad / s作匀角速度运动时 , 连杆的角速度 ω2 ≈ 48 rad / s(图 3 ( a) 所示 ) ;滑块 m 的位移变化范围是 90 150 mm (图 3 ( b) 所示 ) ;滑块 m 的速度变化范 mm 围大约是 ±0. 6 ×104 mm / s (图 3 ( c) 所示 ) 。而且 它们在 0. 07 s内变化了 2个周期 。 3　曲柄滑块机构的匀角加速度运动学 仿真 [ 6 - 9 ] 1　匀角加速度输入时曲柄滑块机构的 Simulink 3 仿真模型 　　曲柄连杆机构的曲柄以 α1 = 8 rad / s2作匀角加 速度运动 。研究在这一输入作用下的曲柄连杆机构 连杆的运动角速度变化规律以及滑块的位移 、加速 图 4　曲柄匀角加速运动时的仿真模型 F ig. 4 S im ula tion m odel of the brace hom ogeneous angle accelera tion sport 度的变化规律 。应用图 4曲柄匀角加速运动时的仿 真模型 MATLAB 算法建立计算曲柄滑块机构的加 速度方程 (8)的 MATLAB 函数模块 slipblock_accel d2 l0 d t2 ) 。应用该 MATLAB Function模块建立的 Simulink 仿真模型如图 4所示 。仿真初始条件 : θ1 =θ2 = 0 l0 = 0 mm / s、ω1 =ω2 = 0 rad / s。 rad、l0 = 150 mm、 eration (该模块 in: α1、ω1、ω2、θ1、θ2 ; out: α2、 2　匀角加速度输入时曲柄滑块机构 Simulink仿 3 真曲线分析 　　曲柄连杆机构的曲柄以 α1 = 8 rad / s2作匀角加 速度运动时 (对应图 4的仿真模型 ) ,连杆的运动 　　角速度 ω2 的仿真曲线如图 5 ( a) 所示 。滑块 m 的位移仿真曲线如图 5 ( b) 所示 ,加速度仿真曲线如 图 5 ( c) 所示 。 从 仿 真 曲 线 可 以 看 出 , 当 曲 柄 以 α1 = 8 rad / s2 (仿真初始条件 :θ1 = θ2 = 0 rad、l0 = 150 mm、ω1 =ω2 = 0 rad / s、 l0 = 0 mm / s。) 作匀角加速 度运动时 ,连杆的 ω2 从 0开始按图 5 ( a) 规律变化 增加 ,大约 4秒时其绝对值达到 7 rad / s ;滑块 m 的 位移范围也是 90 mm 150 mm,只是位移变化先慢后 快 (图 5 ( b) 所示 ) ;滑块 m 的加速度按图 5 ( c) 的规 律变化增加 , 大约 4 秒时其绝对值达到 3. 6 ×104 mm / s2。 ( a) ( b) ( c) 图 5　匀角加速运动时曲柄连杆机构的 Simulink仿真曲线 F ig. 5 Brace b ind iny m echan ism sim ulink sim ula tion curve of the hom ogeneous angle accelera tion sport 4　利用匀角加速度输入 Simulink仿真 模型进行曲柄滑块机构在匀角速度作 用下的仿真 [ 6 - 9 ] 　　应用图 4所示的“曲柄匀角加速运动时的仿真 模型 ”对曲柄滑块机构在匀角速度作用下进行仿 真 ,需要对图 4作一局部调整 ,令图 4中的 MATLAB Function模块的第一个输入 alpha1 (α1 )为 0,第二个 输入 omega1 (ω1 ) 等于 188. 5 rad / s ,得到如图 6所 示的新模型 。应用新模型进行仿真 ,得到仿真曲线 如图 7所示 ,其中图 7 ( a) 、图 7 ( b)分别表示匀角速 度运动时曲柄连杆机构连杆的角速度 ω3 和滑块位 移 l0 的仿真曲线波形 ,这与图 3 ( b) 、图 3 ( a) 波形完 

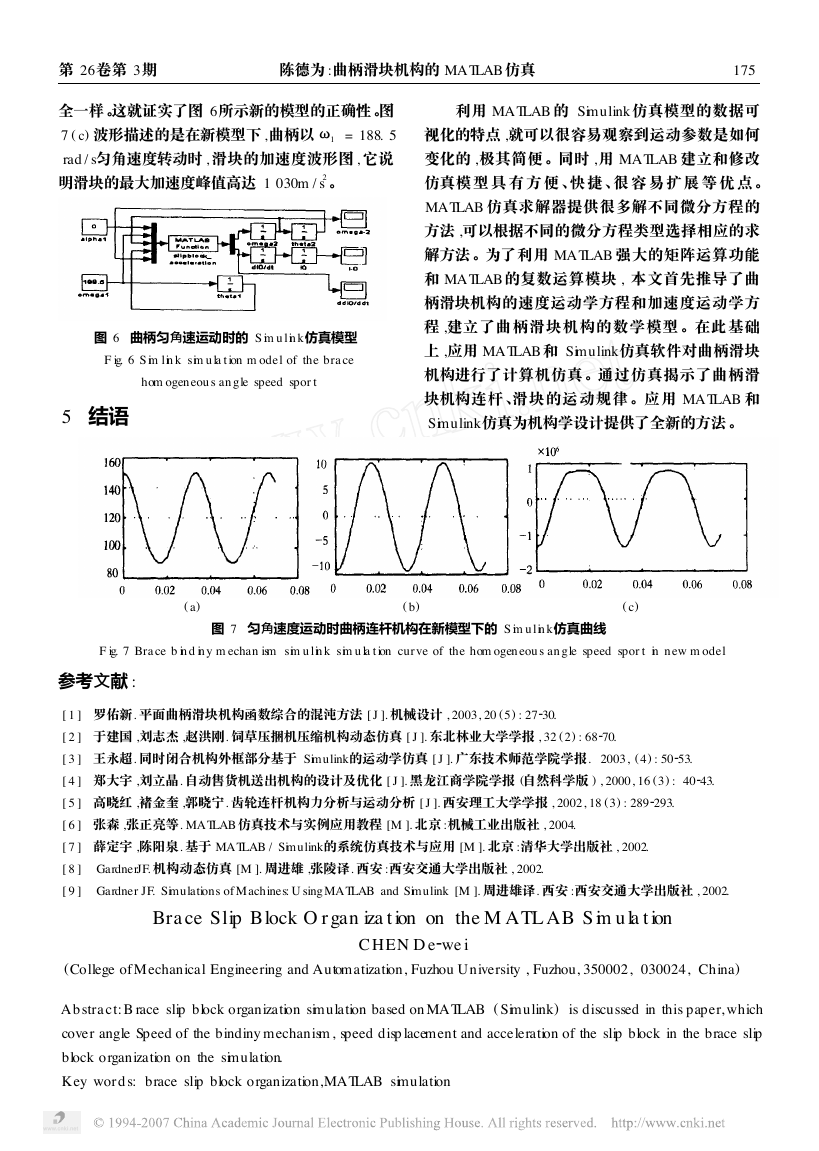
第 26卷第 3期 　　　　　　　　陈德为 :曲柄滑块机构的 MATLAB仿真 571 全一样 。这就证实了图 6所示新的模型的正确性 。图 7 ( c) 波形描述的是在新模型下 ,曲柄以 ω1 = 188. 5 rad / s匀角速度转动时 , 滑块的加速度波形图 , 它说 明滑块的最大加速度峰值高达 1 030m / s2。 图 6　曲柄匀角速运动时的 S im ulink仿真模型 F ig. 6 S im link sim ula tion m odel of the brace hom ogeneous angle speed sport 5　结语 　　利用 MATLAB 的 Simulink仿真模型的数据可 视化的特点 ,就可以很容易观察到运动参数是如何 变化的 ,极其简便 。同时 ,用 MATLAB 建立和修改 仿真模 型 具 有 方 便 、快 捷 、很 容 易 扩 展 等 优 点 。 MATLAB 仿真求解器提供很多解不同微分方程的 方法 ,可以根据不同的微分方程类型选择相应的求 解方法 。为了利用 MATLAB 强大的矩阵运算功能 和 MATLAB的复数运算模块 , 本文首先推导了曲 柄滑块机构的速度运动学方程和加速度运动学方 程 ,建立了曲柄滑块机构的数学模型 。在此基础 上 ,应用 MATLAB和 Simulink仿真软件对曲柄滑块 机构进行了计算机仿真 。通过仿真揭示了曲柄滑 块机构连杆 、滑块的运动规律 。应用 MATLAB 和 Simulink仿真为机构学设计提供了全新的方法 。 ( a) ( b) ( c) 图 7　匀角速度运动时曲柄连杆机构在新模型下的 S im ulink仿真曲线 F ig. 7 Brace b ind iny m echan ism sim ulink sim ula tion curve of the hom ogeneous angle speed sport in new m odel 参考文献 : [ 1 ] 　罗佑新. 平面曲柄滑块机构函数综合的混沌方法 [ J ]. 机械设计 , 2003, 20 (5) : 27 [ 2 ] 　于建国 ,刘志杰 ,赵洪刚. 饲草压捆机压缩机构动态仿真 [ J ]. 东北林业大学学报 , 32 (2) : 68 [ 3 ] 　王永超. 同时闭合机构外框部分基于 Simulink的运动学仿真 [ J ]. 广东技术师范学院学报. 2003, (4) : 50 53. [ 4 ] 　郑大宇 ,刘立晶. 自动售货机送出机构的设计及优化 [ J ]. 黑龙江商学院学报 (自然科学版 ) , 2000, 16 (3) : 40 [ 5 ] 　高晓红 ,褚金奎 ,郭晓宁. 齿轮连杆机构力分析与运动分析 [ J ]. 西安理工大学学报 , 2002, 18 (3) : 289 [ 6 ] 　张森 ,张正亮等. MATLAB仿真技术与实例应用教程 [M ]. 北京 :机械工业出版社 , 2004. [ 7 ] 　薛定宇 ,陈阳泉. 基于 MATLAB / Simulink的系统仿真技术与应用 [M ]. 北京 :清华大学出版社 , 2002. [ 8 ] 　GardnerJF. 机构动态仿真 [M ]. 周进雄 ,张陵译. 西安 :西安交通大学出版社 , 2002. [ 9 ] 　Gardner JF. Simulations of Machines: U sing MATLAB and Simulink [M ]. 周进雄译. 西安 :西安交通大学出版社 , 2002. 293. 43. 30. 70. Brace Slip Block O rgan iza tion on the M ATLAB S im ula tion CHEN D e we i (College of Mechanical Engineering and Automatization, Fuzhou University , Fuzhou, 350002, 030024, China) Abstract:B race slip block organization simulation based on MATLAB ( Simulink) is discussed in this paper, which cover angle Speed of the bindiny mechanism , speed disp lacement and acceleration of the slip block in the brace slip block organization on the simulation. Key words: brace slip block organization,MATLAB simulation