logo资料库

交直流电力系统区域振荡混合控制策略.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：1.03M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    第 34 卷第 8 期 ２０14 年 8 月 电 力 自 动 化 设 备 Ｅｌｅｃｔｒｉｃ Ｐｏｗｅｒ Ａｕｔｏｍａｔｉｏｎ Ｅｑｕｉｐｍｅｎｔ Ｖｏｌ．34 Ｎｏ．8 Aug. ２０14 交直流电力系统区域振荡混合控制策略 马燕峰 1，杜江龙 1，2，赵书强 1 （1. 华北电力大学 电力工程系，河北 保定 071003；2. 天津市电力公司，天津 300072） 摘要： 通过计算模式阻尼比对机组有功出力和直流线路有功功率的灵敏度，得到参与振荡模式的关键机组和 直流线路。 提出基于阻尼比灵敏度的由机组出力调整和直流传输功率调整两部分组成的混合控制策略，以此 抑制大区域电网的区域功率振荡。 在软件 DIgSILENT 中搭建了 8 机交直流电力系统，通过策略实施前后的结 果对比，表明所提控制策略能够有效地抑制交直流电力系统的区域振荡，提高了系统的稳定性。 关键词： 交直流电力系统； 阻尼比； 灵敏度分析； 振荡； 控制； DIgSILENT； 稳定性； 遗传算法 中图分类号： TM ７１２ DOI： 10.3969 ／ j.issn.1006－6047.2014.08.010 文献标识码： A 0 引言 随着全国联网的战略规划持续推行，直流输电 在长距离输电中扮演着重要角色，但大区域交直流 电力系统的安全稳定问题非常复杂，而低频振荡不仅 成为严重危及互联系统安全运行的重要因素，还制约 着系统间功率传输。 因此，对交直流电力系统功率 振荡进行研究，并采取相应的控制策略具有重要的理 论价值和现实意义。 目前，PSS 仍是增强系统阻尼、抑制电网低频振 荡的首选，但 PSS 对区域模式阻尼效果不明显，大量 安装问题复杂，而基于广域信号的 PSS 仍处于理论 研究阶段 ［1鄄2］；此外，STATCOM、TCSC 等 FACTS 设备 也具有抑制低频振荡的作用 ［3］，但现场安装不普遍。 对于交直流电力系统 ，PSS 和直流调制等附加控 制 的协调也是难点 ［4］。 文献［5鄄7］提出在大电网的区域 振荡中，采用降低关键机组出力（包括解列机组）、提 高直流功率、降低交流通道功率等一次侧措施抑制 系统低频振荡。 作为阻尼控制器的补充，合理调整 系统运行方式将使振荡获得良好的阻尼。 文献［1，8］ 以参与因子作为求取与振荡模式强相关机组的性能 指标，并提出相应的调出力策略，但参与因子不能明 确机组参与的方向信息。 文献［9］从特征值灵敏度的 角度阐述了运行方式与小干扰稳定的关系，并给出了 灵敏度的计算方法；文献［10］提出了特征值对运行 参数的灵敏度；文献［11鄄12］计算了特征值对运行参 数的灵敏度，分析了它们对系统小干扰稳定的影响； 收稿日期：2013-07-17；修回日期：2014－06－03 基金项目：中央高校基本科研业务费专项资金资助项目（2014鄄 MS88） ； 国家电网公司大电网重大专项资助项目（SGCC- MPLG鄄 019-2012）；河北省自然科学基金资助项目（E2011502014） Project supported by the Fundamental Research Funds for the Central Universities （2014MS88） ，State Grid Corporation of China，Major Projects on Planning and Operation Control of Large Scale Grid（SGCC鄄MPLG019鄄2012） and the Natural Science Foundation of Hebei Province（E2011502014） 文献［13鄄14］在特征值灵敏度基础上计算了阻尼比灵 敏度，并通过合理地安排机组的出力以改善小干扰稳 定性影响的功率传输能力。 目前，特征值对运行灵敏 度的研究多集中在交流系统和调整机组出力，而应用 于交直流系统、将调整机组出力和直流线路功率相结 合制定控制策略的相关研究并不多见。 本文提出基 于 阻 尼 比 灵 敏 度 的 混 合 控 制 策 略 ， 利用调整机组出力抑制振 荡 的 快 速 有 效 性 ，以 及 直 流输电的高度可控、短时过负荷、快速改变潮流等特 点，将 ２ 种方式配合来提高模式阻尼。 在阻尼比对发 电机有功出力和直流有功 潮 流 的 灵 敏 度 的 基 础 上 ， 采用优化算法得出机组出 力 和 直 流 功 率 的 调 整 值 ， 将阻尼比提高至安全阈值 ，当 所 有 模 式 的 阻 尼 比 均 在安全范围内 ，则系统达 到 稳 定 要 求 。 最 后 以 8 机 交 直流电力系统为例 ，仿真验证 该 控 制 策 略 的 合 理 性和有效性。 1 交直流系统的灵敏度计算 1.1 交直流系统模型 发电机采用考虑凸极效应和机械阻尼时的二阶 模型，如式（1）所示 ［15］。 Ud= XqIq Uq= E′q- X′dId Δ                 MΔω觶 = ΔPm- ΔPe- ＤΔω ＝ - ΔPe- ＤΔω Δδ觶 ＝ Δ ω （1） 其 中 ，Ud、Uq、Id、Iq、Xq、X′d、E′q 依 次 为 发 电 机 的 d 轴 电 压、q 轴电压、d 轴电流、q 轴电流、q 轴同步电抗、d 轴 暂 态 电 抗 、q 轴 暂 态 电 势 ；Ｍ 为 转 子 惯 性 时 间 常 数 ； ΔPe ＝ ＫΔδ，Ｋ 为 同 步 力 矩 系 数 ；D 为 阻 尼 转 矩 系 数 ； Δω、Δδ 分别为转子角速度和功角的微增量。 忽略分布电容，整流侧采取定电流控制，逆变侧 采取定电压控制，考虑简化的惯性放大调节器以及控 制器的调节时间常数，直流系统模型为 ［16］：
    第 8 期 马燕峰，等：交直流电力系统区域振荡混合控制策略 i                           Udr = 3 Udi = 3 ２姨 nr Ur cos α ／ π－ 3Xcr Id ／ π ２姨 ni Ui cos β ／ π+ 3Xci Id ／ π Id= Ur nr［cos α - cos（α ＋ γ）］ ／ （ T1Δα觶 = -Δα + Ｋ1ΔId+ Ｋ1ΔUsr T2Δ β觶 = -Δ β -Ｋ2Udi + Ｋ2ΔUsi Ｘd I觶 d= -RdId+ Udr - Udi ２姨 Ｘcr） （2） 其中，Udr、Ur、Usr 分别为整流器直流侧、交流侧电压和电 压设定值；Udi、Ui、Usi 为逆变器直流侧、交流侧电压和电 压设定值；nr、ni、Ｘcr、Ｘci 为换流变压器的变比和换相 电抗 ；Id 为直流线路电流 ；Rd、Xd 分别为直流线路电 阻 和 电 抗 ，Xd 中 包 含 平 波 电 抗 ；α、β、γ 分 别 为 触 发 角、触发超前角、换相角；Ｋ１、Ｋ２ 分别为定电流和定电 压控制的惯性环节放大系数；Ｔ1、Ｔ2 为时间常数。 交流网络采用准稳态模型，只保留发电机节点 和直流节点，消去联络节点后的线性化模型为 ［17］： 取。 于是，第 k 个特征值对第 i 个参数 Ｐi 的灵敏度可 表示为： λk Ｐi 2n λk Um = 鄱 m＝1 Um Ｐi 2n λk Im + 鄱 m＝1 Im Ｐi （6） 其中，n 为网络节点数。 阻尼比灵敏度在特征值灵敏度基础上计算 ［13］： ξk Ｐi ＝ 1 α２ k＋ ω２ k 1 k＋ ω２ α２ k 姨 姨 - ω２ k α２ k＋ ω２ k αk Ｐi + α kωk α２ k＋ ω２ k ωk Ｐi （7） 其 中 ， αk Ｐi 、 ωk Ｐi 虚部。 分 别 为 相 应 特 征 值 灵 敏 度 实 部 和 特征值灵敏度能反映参数 Ｐi 变化引起的特征值 变化；阻尼比反映系统振荡模式衰减的快慢，其灵敏 度更直观地反映了运行参数对系统稳定的影响程度 和方向，可明确需要调整的机组和直流线路。 ΔUxyF ΔUxyy = ZFL ΔIxyF ΔIxyy y （3） 2 基于阻尼比灵敏度的控制策略 其 中 ，ΔUxyF、ΔIxyF、ΔUxy、ΔIxy 分 别 为 各 发 电 机 和 各 换 流站电压、电流的偏差量在系统公共 x - y 坐标系中 的分量；ZFL 为实部和虚部分开的阻抗矩阵。 对发电机和直流换流器模型的代数方程进行线 性化，并将发电机方程转化为同步坐标，则建立交直 流电力系统标准的状态方程为 X觶 = AX，其中，A 为状 态系数矩阵，内含各机组和换流站节点直角坐标形 式的电压和电流。 X 为： X ＝ ［Δδ１ … Δδn Δω1 … Δωn Δα1 Δβ1 ΔId1 … Δαl Δβl ΔIdl］ T （4） 1.2 阻尼比灵敏度计算 对于状态矩阵 A，特征值为 λk=αk+jωk，αk 为衰减 α２ k＋ ω２ k 姨 kA = vT 系数，ωk 为振荡角频率，阻尼比为 ζk=-αk ／ ， 有 Auk= λkuk 和 vT kλk，其中 vk、uk 分别为 λk 的左、 右特征向量。 设矩阵 A 是运行参数 σ 的函数，则有 A （α）uk = λkuk，则 λk、uk 为 σ 的隐函数 ，等式两边对 σ 求偏导数 ，然后左乘 vT k ，整理可 得 特 征 值 λk 对 σ 的灵敏度为 ［15］： uk vT k Ａ（σ） σ vT k uk λk σ ＝ （5） λk σ 是复数，反映 σ 微小变化时 λk 的移动方向 （相位）和大小。 Ａ（σ） σ 取稳态工况下的 σ 值计算。 当 σ 取 为 发 电 机 节 点 和 换 流 站 节 点 的 有 功 功 率 Ｐi 时，由于 Ｐi 不直接显含在 Ａ 中， λk Ｐi 不能直接得到， 需借助节点 i 处的电压和电流作为中间变量进行求 模式的阻尼比反映了模式的稳定性，通过计算阻 尼比对机组出力和直流有功潮流的灵敏度 ，调 整 灵 敏度高的机组或直流线路传输功率 ，可以快速提高 相应模式的阻尼比。 当模式的阻尼比不低于可接受 的安全值 ζ1im 时，系统的小干扰稳定性得以保证 ，文 中取 ζ1im= 3%。 2.1 控制策略求解 根据低频振荡产生机理、灵敏度分析方法和交直 流混合电力系统的客观条件，控制策略求解步骤如下。 a. 潮流计算。 通过潮流计算，求得各发电机、换 流站节点的电压、电流等数据。 b. 特征分析。 计算矩阵 A 的特征根、阻尼比、参 与因子等，确定弱阻尼振荡模式及主要参与机组。 c. 阻尼比灵敏度计算。 针对区域弱阻尼模式，通 过式（5）—（7）求解该模式下对机组有功出力 ＰG1、ＰG2、 …、ＰGm 和直流传输功率 ＰD1、ＰD2、…、ＰDl 的阻尼比灵敏 度。 设 Ski = ζk Ｐi ，则 SkGi 和 SkDi 分别为第 k 个振荡模 式 阻尼比对发电机 i 的有功出力和直流线路 i 的有 功输送的灵敏度。 d. 灵敏度排序。 提取弱阻尼振荡模式 k 的阻尼 比灵敏度，并分别对 SkG1、SkG2、…、SkGm 和 SkD1、SkD2、…、 SkDl 进行排序。 当 Ski ＞ 0 时，即该元件与阻尼比正相 关，增加 Ｐi，可以提高模式阻尼；同理，当 Ski ＜ 0 时，则 减小 Ｐi。 e. 策略制定。 根据步骤 d 的灵敏度，为了使所有 模式阻尼均满足小干扰稳定性的要求，在调节代价最 小的情况下，以阻尼比灵敏度为指标，采用优化算法 求取各发电机和直流线路的调整量。 目标函数为：
    电 力 自 动 化 设 备 第 34 卷 C = min（鄱 ΔＰGi + 鄱 ΔＰDi ） （8） 其中， ΔＰGi 为发电机 i 调整量的绝对值； ΔＰDi 为 直流线路 i 调整量的绝对值。 研究表明，系统结构不变和运行方式变化不大时， 阻尼比灵敏度 Ｓki 与 Pi 呈近似线性关系 ［14］，因此系统 调整后的阻尼比应满足如下关系： ζ1im-ζj0≤鄱（SjGiΔPGi）+鄱（SjDiΔPDi ） j=1，…，m1 （9） 其中，ζj0 为第 j 个弱阻尼振荡模式的阻尼比初值；m1 为系统中需要提高的弱阻尼振荡模式数。 除此之外，还应考虑发电机发出功率和直流线路 输送功率的限值以及系统的功率平衡： ＰGimin-ＰGi0≤ΔPGi≤ ＰGimax-ＰGi0 ＰDimin-ＰDi0≤ΔPDi≤ ＰDimax-ＰDi0 鄱PGi-鄱PLi= 0 （10） （11） （12） 其中，ＰGimax 和 ＰGimin 分别为发电机 i 的有功出力上、下 限值； ＰDimax 和 ＰDimin 分别为直流输电线 i 的输送容量 上、下限值；下标 0 表示相应变量稳态值；PLi 为节点 i 负荷。 上述控制策略可以采用优化方法求取。 f. 策略校验。 通过自动发电控制（AGC）或调度 人员命令实施上述控制策略后，校验是否产生新的弱 阻 尼 振 荡 模 式 。 若 产 生 ，则 转 步 骤 a；否则，优化结 果即为最终控制策略。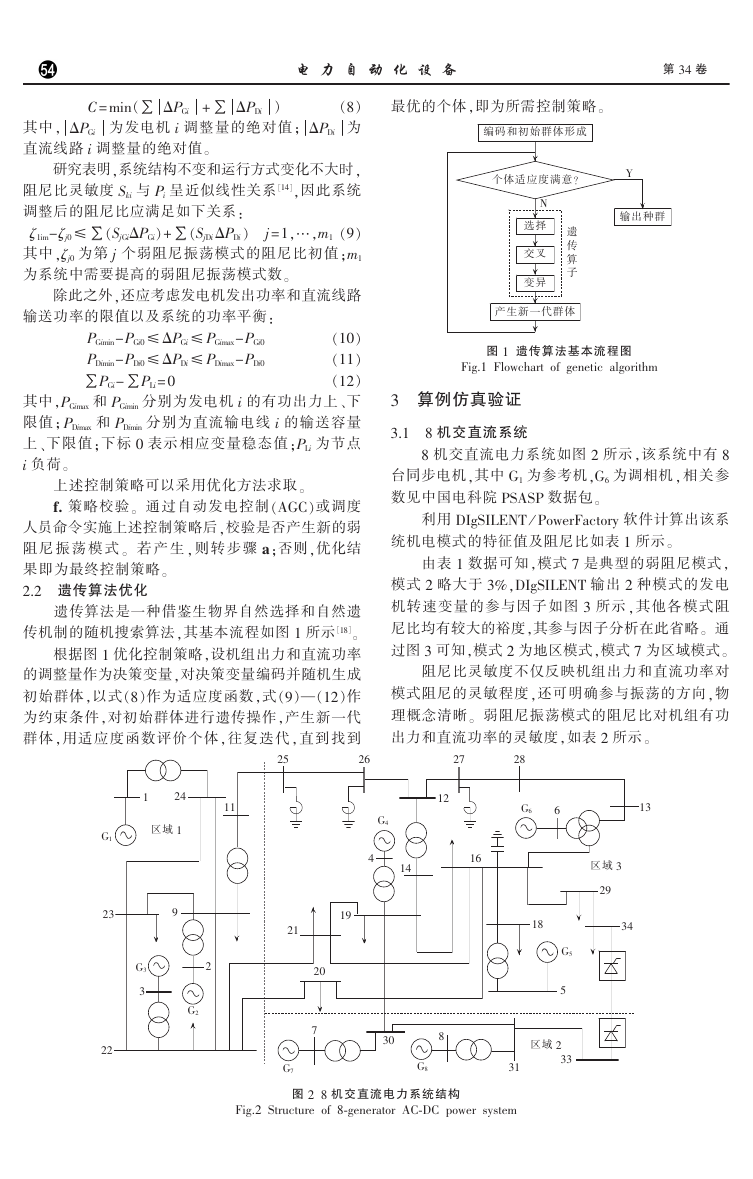 2.2 遗传算法优化 遗传算法是一种借鉴生物界自然选择和自然遗 传机制的随机搜索算法，其基本流程如图 1 所示 ［18］。 根据图 1 优化控制策略，设机组出力和直流功率 的调整量作为决策变量，对决策变量编码并随机生成 初始群体，以式（8）作为适应度函数，式（9）—（12）作 为约束条件，对初始群体进行遗传操作，产生新一代 群体，用适应度函数评价个体，往复迭代 ，直到找到 最优的个体，即为所需控制策略。 编码和初始群体形成 个体适应度满意？ Ｙ 输出种群 Ｎ 选择 交叉 变异 遗 传 算 子 产生新一代群体 图 1 遗传算法基本流程图 Fig.1 Flowchart of genetic algorithm 3 算例仿真验证 3.1 8 机交直流系统 8 机交直流电力系统如图 2 所示，该系统中有 8 台同步电机，其中 Ｇ1 为参考机，Ｇ6 为调相机 ，相 关 参 数见中国电科院 PSASP 数据包。 利用 DIgSILENT ／ PowerFactory 软件计算出该系 统机电模式的特征值及阻尼比如表 1 所示。 由表 1 数据可知，模式 7 是典型的弱阻尼模式， 模式 2 略大于 3%，DIgSILENT 输出 ２ 种模式的发电 机转速变量的参与因子如图 3 所示 ，其他各模式阻 尼比均有较大的裕度，其参与因子分析在此省略。 通 过图 3 可知，模式 2 为地区模式，模式 7 为区域模式。 阻尼比灵敏度不仅反映机组出力和直流功率对 模式阻尼的灵敏程度，还可明确参与振荡的方向，物 理概念清晰。 弱阻尼振荡模式的阻尼比对机组有功 出力和直流功率的灵敏度，如表 2 所示。 25 26 27 28 1 24 11 G1 区域 １ 12 G4 4 14 16 ２３ 9 19 21 G3 3 2 G2 22 20 7 G7 G6 6 13 区域 3 29 18 34 G5 5 30 8 G8 区域 ２ 33 31 图 2 8 机交直流电力系统结构 Fig.2 Structure of 8鄄generator AC鄄DC power system
    第 8 期 马燕峰，等：交直流电力系统区域振荡混合控制策略 表 1 机电模式特征值及阻尼比 Tab.1 Eigenvalue and damping ratio of electromechanical mode 机电振荡模式 特征值 阻尼比 1 2 3 4 5 6 7 １.00 0.50 -6.473 ± j15.237 0.391 000 -0.425 ± j13.966 0.030 417 -0.391 ± j10.258 0.038 089 -0.435 ± j9.100 -1.507 ± j8.524 -0.272 ± j6.297 -0.095 2 ± j5.021 0.047 748 0.174 100 0.043 155 0.018 957 1.00 0.50 -1.00 -0.50 0.50 1.00 -1.00 -0.50 0.50 1.00 -0.50 -1.00 -0.50 -1.00 （a） 模式 ２ （b） 模式 ７ 图 3 模式 2 和模式 7 转速变量参与因子 Fig.3 Participation factor of speed in mode 2 and mode 7 表 2 模式 2 和模式 7 的阻尼比灵敏度 Tab.2 Damping ratio sensitivity of mode 2 and mode 7 有功功率 PG1 PG2 PG3 PG4 PG5 PG7 PG8 PD1 阻尼比灵敏度 模式 2 -0.000 462 0.000 374 0.000 186 -0.000 085 -0.000 063 -0.000 076 -0.000 051 -0.000 045 模式 7 0.000 098 0.000 159 0.000 247 0.000 508 0.000 392 -0.000 523 -0.000 415 0.000 397 设初始群体为 20，交叉概率为 0.8，每代优选子 辈为 2。 利用遗传算法计算出考虑直流调整和不考 虑直流调整 2 种情况下的控制策略 ，以及实施控制 策略之后系统的阻尼比分别如表 3 和表 4 所示。 表 3 不考虑直流调整时系统有功调节量及 调整后的阻尼比 Tab.3 Amount of active power regulation and corres鄄 ponding damping ratio，without DC adjustment ΔPG4 ／ MW ΔPG７ ／ MW 10.75 -10.75 机电模式阻尼比 模式 2 0.030 320 模式 7 0.030 040 表 4 考虑直流调整时系统有功调节量及调整后的阻尼比 Tab.4 Amount of active power regulation and corres鄄 ponding damping ratio，with DC adjustment ΔPG4 ／ MW ΔPG７ ／ MW ΔPD1 ／ MW 机电模式阻尼比 模式 2 模式 7 3.2.1 设定负荷扰动 在 51 s 时，节点 19 的负荷突增 40 MW，持续 2 s 后恢复，节点 19 与节点 30 的联络线 19-30 的振荡 曲线如图 4 中实线所示。 Ｗ Ｍ ／ 率 功 300 280 260 240 220 调整前 调机组 Ｇ４、G7 调机组 Ｇ４、G7 和直流 50.00 57.75 65.50 时间 ／ s 73.25 81.00 图 4 节点 19 的负荷突增扰动，调控前后的振荡曲线 Fig.4 Tie鄄line oscillation curve responding to sudden load increase of bus19，comparison between with and without control measures 对系统实施同样扰动，在 58 s 时，实施表 3 控制 策略，振荡曲线如图 4 中虚线所示；实施表 4 控制策 略，振荡曲线如图 4 中点划线所示。 仿真结果表明， 实施策略后，振荡曲线快速收敛，阻尼振荡效果明显。 3.2.2 设定断线扰动 当 51 s 时，交流联络线 19-30 发生单相断线扰 动，1.5 s 后重合，联络线 19-30 上发生大幅度的功率 振荡，如图 5 中实线所示。 Ｗ Ｍ ／ 率 功 300 260 220 180 140 调整前 调机组 Ｇ４、G7 调机组 Ｇ４、G7 和直流 50.00 57.75 65.50 时间 ／ s 73.25 81.00 图 5 线路 19-30 单相断线扰动，调控前后的振荡曲线 Fig.5 Tie鄄line oscillation curve responding to single鄄 phase break and reclose，comparison between with and without control measures 对系统实施同样扰动 ，分别实施表 3 和表 4 的 控制策略，振荡曲线分别如图 5 中虚线和点划线所 示。 仿真结果表明，区域功率振荡收敛效果明显，有 力说明该策略对提高系统稳定性和抑制区域振荡的 有效性。 同时，通过图 4 和图 5 不同控制策略的比较可 知，当控制策略考虑直流线路输送功率时，在达到同 样阻尼比要求时，可以使机组的功率调整量减小，同 时协调考虑直流线路和机组有功出力调整，可以减小 交流线的功率振荡，使系统快速进入稳定状态。 8.45 -8.45 6.1 0.030 064 0.030 078 总之，仿真验证了基于阻尼比灵敏度抑制区域振 3.2 仿真分析 荡的混合控制策略，在二次系统阻尼控制效果不明显 选择负荷变化和断线 ２ 种具有代表性的扰动 ， 时，根据阻尼比灵敏度调整机组有功出力或直流功率， 对比采取控制策略前后的结果加以分析。 可有效地抑制区域模式的低频振荡。 面对日益庞大
    电 力 自 动 化 设 备 第 34 卷 和复杂的电网，此策略可为调度人员决策提供参考， 弥补仅靠经验判断的不足。 4 结语 本文针对交直流混合电网区域功率振荡，提出基 于阻尼比灵敏度的机组出力及直流功率调整的混合 控制策略。 该策略从潮流控制的角度 ，调整关键机 组出力，减弱振荡能量；提高关联紧密的直流线路功 率，控制电网潮流分布，及时防止振荡恶化。 通过阻 尼比灵敏度明确参与振荡模式的关键机组和直流线 CHE N Zhong. Real鄄time stability control of power system with small disturbance ［ J ］ . Electric Power Automation Equipment ， 2012，32（3）：42鄄46. ［7］ KLELN J W，KRANSE P C，FERNANDES L A. Investigation of DC modulation in parallel AC ／ DC power system［C］∥IEEE Winter Meeting. New York，USA：［s.n.］，１９７８：２３５鄄２３８. ［8］ 徐伟，鲍颜红，徐泰山，等. 电力系统低频振荡实时控制［J］. 电力 自动化设备，2012，32（5）：98鄄101. XU Wei，BAO Yanhong，XU Taishan，et al. Real鄄time control of power system low鄄frequency oscillation［J］. Electric Power Auto鄄 mation Equipment，2012，32（5）：98鄄101. ［9］ 刘晓鹏，吕世荣，郭强，等. 特 征 值 对 运 行 方 式 灵 敏 度 的 计 算 ［J］. 电力系统自动化，1998，22（12）：9鄄12. 路，适当调整机组出力或直流功率将模式阻尼比提 LIU Xiaopeng，L譈 Shirong，GUO Qiang，et al. Eigenvalue sensitivity 升至安全值，改善了交直流系统的全局阻尼能力，从 整体上提高了系统的稳定性。 以 8 机交直流系统为 例，仿真验证了该策略的有效性 。 但是本文控制策 against operating condition in power system ［J ］. Automation of Electric Power Systems，1998，22（12）：9鄄12. ［10］ WANG K W，ChUNG C Y，TSE C T，et al. Multimachine eigen鄄 value sensitivities of power system parameters［J］. IEEE Trans 略制定时只考虑了系统的功率调整量最小，没有考虑 on Power Systems，2000，15（2）：741鄄747. 到不同机组有功出力调整以及与直流输送功率调整 的经济代价不同，也没有考虑到控制策略实施的时间 ［11］ MA Jian，DONG Zhaoyang，ZHANG Pei. Eigenvalue sensitivity analysis for dynamic power system［C］∥International Conference on Power System Technology，2006. Chongqing，China：［s.n.］， 问题，这将是笔者下一步研究的内容。 ２００６：１鄄７. 另外，随着基于 GPS 和 PMU 的广域测量系统在 电网中的不断推广，得到全网实时运行的动态信息成 为可能，利用广域在线数据计算得到类似阻尼比灵敏 ［12］ 马林，廖培金，彭书涛. 小干扰稳定中特征值对运行参数的灵敏 度［J］. 电力系统及其自动化学报，2005，17（4）：31鄄35. MA Lin，LIAO Peijin，PENG Shutao. Eigenvalue sensitivity with respect to operating parameters in small signal stability analysis 度的性能指标，进而提出实用性更强的广域调度控制 ［J］. Proceedings of the CSU鄄EPSA，2005，17（4）：31鄄35. 策略是本文进一步的研究方向。 参考文献： ［13］ CHUNG C Y，WANG Lei，HOWELL F，et al. Generation resche鄄 duling methods to improve power transfer capability constrained by small鄄signal stability ［J］. IEEE Transactions on Power Sys鄄 tems，2004，19（１）：524鄄530. ［1］ 鲍颜红，徐伟，徐泰山，等. 基于机组出力调整的小干扰稳定辅助 ［14］ 刘家岩. 计及小干扰稳定约束的发电机有功再调度［D］. 吉林： 决策计算［J］. 电力系统自动化，2011，35（3）：88鄄91. BAO Yanhong，XU Wei，XU Taishan，et al. Small鄄signal stability 东北电力大学，2008. LIU Jiayan. The generator active rescheduling with considering auxiliary decision鄄making calculation based on power generation the small signal stability constraint［D］. Jilin：Northeast Electric adjustment［J］. Automation of Electric Power Systems ，2011 ，3 5 Power University，2008. （3）：88鄄91. ［15］ 倪 以 信 ，陈 寿 孙 ，张 宝 霖. 动 态 电 力 系 统 的 理 论 和 分 析 ［M］. 北 ［2］ 陈 晓 明. 基 于 广 域 测 量 系 统 的 电 力 系 统 低 频 振 荡 分 析 及 抑 制 综 京：清华大学出版社，2002：252鄄258. 述［J］. 现代电力，2007，24（6）：12鄄16. CHEN Xiaoming. Analysis and suppression of low frequency os鄄 cillation inpower system based on WAMS ［J ］. Modern Electric Power，2007，24（6）：12鄄16. ［3］ 王 康 ，金 宇 清 ，甘 德 强 ，等. 电 力 系 统 小 信 号 稳 定 分 析 与 控 制 综 述［J］. 电力自动化设备，2009，29（5）：10鄄19. WANG Kang，JIN Yuqing，GAN Deqiang，et al. Survey of power system small signal stability and control［J］. Electric Power Auto鄄 mation Equipment，2009，29（5）：10鄄19. ［4］ 魏巍，王渝红，李兴源，等. 交直流电力系统 PSS 和直流附加控制 ［16］ 韩 英 铎 ，王 仲 鸿 ，陈 淮 金. 电 力 系 统 最 优 分 散 协 调 控 制 ［M］. 北 京：清华大学出版社，1997：62鄄72. ［17］ 马燕峰. 交直流混合电力系统低频振荡协调稳定控制［D］. 保定 ： 华北电力大学，2003. MA Yanfeng. Coordinated stabilized control of low鄄frequency oscillation of AC ／ DC hybrid power system ［D］. Baoding：North China Electric Power University，2003. ［18］ 雷 英 杰 ，张善文. MATLAB 遗传算法工具箱及应用［M］. 西安 ：西 安电子科技大学出版社，2005：1鄄10. 的协调［J］. 电力自动化设备，2010，30（1）：53鄄57. WEI Wei，WANG Yuhong，LI Xingyuan，et al. Coordination of 作者简介： PSS and DC additional controller for AC ／ DC power system［J］. Electric Power Automation Equipment，2010，30（1）：53鄄57. ［5］ 梁志飞，肖鸣，张昆，等. 南方电网低频振荡控制策略探讨［J］. 电 力系统自动化，2011，35（16）：54鄄58. LIANG Zhifei，XIAO Ming，ZHANG Kun，et al. Disscussion on control strategy for low frequency osillation in China Southern Power Grid ［J］. Automation of Electric Power Systems，2011，35 （16）：54鄄58. ［6］ 陈中. 电力系统小干扰稳定实时控制［J］. 电力自动化设备，2012，32 马 燕 峰 （1978-），女 ，河 北 迁 西 人 ， 副 教 授 ，博士 ，主要研究方向为电力 系 统 分 析 、运 行与控制； 杜 江 龙 （1986－），男 ，河 北 定 州 人 ， 硕 士 研 究 生 ，主 要 研 究 方 向 为 电 力 系 统 分 析 、运 行与控制（Ｅ鄄ｍａｉｌ：djl308218@sina.com）； 赵书强 （1964－），男 ，河北景县人 ，教 授 ， 博士 ，主要研究方向为电力 系 统 稳 定 分 析 和 马燕峰 （3）：42鄄46. 控制、电力系统规划与可靠性等。
    第 34 卷第 8 期 ２０14 年 8 月 电 力 自 动 化 设 备 Ｅｌｅｃｔｒｉｃ Ｐｏｗｅｒ Ａｕｔｏｍａｔｉｏｎ Ｅｑｕｉｐｍｅｎｔ Ｖｏｌ．34 Ｎｏ．8 Aug. ２０14 带恒功率负荷的直流微电网母线电压稳定控制策略 （1． 武汉大学 电气工程学院，湖北 武汉 430072；2. 海军工程大学 电气工程学院，湖北 武汉 430033） 李玉梅 1，2，査晓明 1，刘 飞 1，孙建军 1 摘要： 呈现负阻尼特性的恒功率负荷与分布式电源接入变换器级联容易导致系统出现振荡，给直流微电网稳 定运行带来隐患。 通过建立带恒功率负荷变换器在平衡点的小信号模型，推导变换器占空比与母线电压的传 递函数，并从理论上分析传统 PI 控制器不能提高系统稳定性的原因，进而提出一种提高直流微电网母线电 压稳定性的新型控制策略。 通过绘制闭环系统的根轨迹图，分析控制器各参数的变化对系统稳定性的影响。 以两源两负荷的直流微电网为例，建立 MATLAB ／ Simulink 仿真模型，仿真结果表明孤岛和并网运行下采用 所提控制策略均可以保证直流微电网稳定运行。 关键词： 微电网； 直流微电网； 恒功率负荷； 振荡； 稳定性； 控制； 电压控制 中图分类号： TM ７１２ 文献标识码： A DOI： 10.3969 ／ j.issn.1006－6047.2014.08.011 0 引言 近年来传统化石能源日趋枯竭，世界各国大力发 展可再生能源。 微电网是将分布式能源、负荷、储能 装 置 及 能 量 变 换 装 置 等 集 成 而 形 成 的 一 个 可 控 单 元，是微型化、模块化发电装置与低压分布式电网结 合的产物，其在提高可再生能源利用率、缓解能源需 求与环境保护之间的矛盾、提高供电的安全性和可 靠性等方面具有重要的意义。 它作为一个独立的整 体，既可以并网运行，也可以孤岛运行。 从结构上分 类，微电网可以分为交流微电网和直流微电网。 交流 微电网可以利用现有的交流系统结构，但并网时与 大电网的同频同相控制实现起来比较复杂，稳定性 问题也比较复杂 ［1鄄2］。 由于大多数可再生能源（如光 伏、燃料电池）和储能装置都是直流的，现代化的电 子负载如计算机、数据中心、通信设备等都是利用直 收稿日期：201４ - 0２ - １１；修回日期：2014 － 0６ － ２０ 基金项目：国家自然科学基金面上项目（51277137） Project supported by the Ｇeneral Program of National Natural Science Foundation of China（51277137） 流供电，大多数电机驱动也需要直流供电（变频电机 用直流供电可以省掉整流电路），而且由于没有集肤 效 应 ，直 流 电 缆 比 交流电缆的传输容量更大，因此从 效率、体积和成本上而言，直流微电网结构都要优于 交 流 微 电 网 结 构 。 但 是 ，直 流 微 电 网 也 存 在 自身的 稳定性问题，尤其是当直流微电网中存在大功率的恒功 率负荷（ＣＰＬ）时，可能会引起直流母线的不稳定 ［3鄄9］。 现有的一些文献对直流微电网母线电压不稳定 机理做了分析，并提出了一些提高稳定性的措施［１０鄄１６］， 其中文献［1１］中提出在源侧变换器与恒功率负荷之 间增加 无 源 阻 尼 装 置 来 提 高 系 统 的 稳 定性，但这种 方法会增大系统的体积和损耗；因此文献［9］中提出 把直流微电网看成一个整体，通过与交流大电网的接 口变换器的控制器增加有源阻尼信号来改变变换器 的等效阻抗，这种方法不需要改变原有系统结构，通 过选取合适的控制器参数就可以极大改善系统的稳 定性，但是没有考虑当直流微电网孤岛运行时，并网 变换器不参加运行，系统的稳定控制问题；文献［1２］ 针对于带恒功率负荷的 DC ／ DC 变换器，通过在输出 ssssssssssssssssssssssssssssssssssssssssssssss Hybrid areal oscillation control strategy of AC鄄DC power system MA Yanfeng1，DU Jianglong1，2，ZHAO Shuqiang1 （1. Department of Electrical Engineering，North China Electric Power University，Baoding 071003，China； 2. Tianjin Electric Power Corporation，Tianjin 300072，China） is Abstract： The sensitivity of mode damping ratio to generator active power or DC line active power calculated to obtain the critical generators or DC lines participating in the oscillation mode，based on which，a hybrid control strategy consisting of regulation and the DC power transmission adjustment large power grid . An 8鄄generator AC鄄DC power system is built in DIgSILENT and the simulative results are compared between with and without the proposed strategy，which shows that，with the proposed strategy， the areal oscillation of AC鄄DC power system is effectively suppressed and the system stability is enhanced. Key words： AC鄄DC power system； damping ratio； sensitivity analysis； oscillation； control； DIgSILENT； stability； genetic algorithms the areal power oscillation of the generator power output is proposed to suppress the implementation of
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料