第二版的 8.17 是第三的 8.22，题目中的 4-Bit 改为 5-bit 第二版的 8.16 是第三版的 8,20 8.20 The input to the LZW decoding algorithm for the example in Example 8.12 is 39 39 126 126 256 258 260 259 257 126 The starting dictionary, to be consistent with the coding itself, contains 512 location-with the first 256 corresponding to gray level values 0 through 255. The decoding algorithm begins by getting the first encoded value, outputting the corresponding value from the dictionary, and setting the” recognized sequence” to the first value. For each additional encoded value, we (1) output the dictionary entry for the pixel value(s), (2) add a new dictionary entry whose content is the “ recognized sequence” plus the first element of the encoded value being processed, and (3) set the “ recognized sequence” to the encoded value being processed. For the encoded output in Example 8.12, the sequence of operations is as shown in Table P8.20. Note, for example, in row 5 of the table that the new dictionary entry for location 259 is 126-39,the concatenation of the currently recognized sequence, 126, and the first element of the encoded value being processed -the 39 from the 39-39 entry in dictionary location 256. The output is then read from the third column of the table to yield 39 39 126 126 39 39 126 126 39 39 126 126 39 39 126 126 where it is assumed that the decoder knows or is given the size of the image that was received. Note that the dictionary is generated as the decoding is carried out. Note that the dictionary is generated as the decoding is carried out. Table P8.20 Pixels 39 39 126 126 39-39 126-126 39-39-126 126-39 39-126 126 Dict. Address Dict. 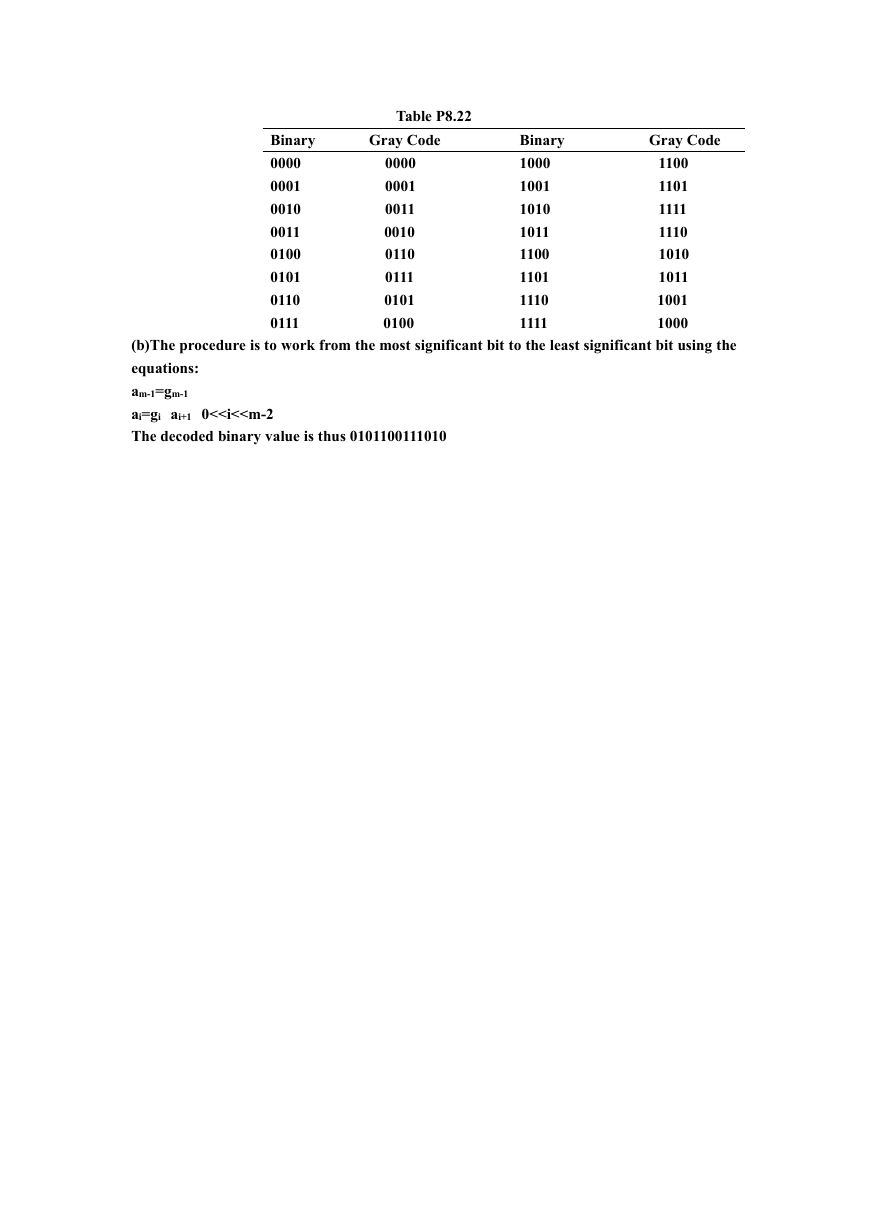Entry 256 257 258 259 260 261 262 263 264 39-39 39-126 126-126 126-39 39-39-126 126-126-39 39-39-126-126 126-39-39 39-126-126 Recognized Encoded Value 39 39 126 126 256 258 260 259 257 39 39 126 126 256 258 260 259 257 126 8.22 (a)Using Eq.(8.4-3),form Table P8.22 

Binary 0000 0001 0010 0011 0100 0101 0110 0111 Table P8.22 Gray Code 0000 0001 0011 0010 0110 0111 0101 0100 Binary 1000 1001 1010 1011 1100 1101 1110 1111 Gray Code 1100 1101 1111 1110 1010 1011 1001 1000 (b)The procedure is to work from the most significant bit to the least significant bit using the equations: am-1=gm-1 ai=gi ai+1 0<