logo资料库

离散数理逻辑练习题与答案.doc

发布时间：2022-06-05 发布人：admin 分类：说明书 资料大小：0.28M 资料格式：doc 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    离散数学(下)单元测试（一） 一、选择题（在每个小题四个备选答案中选出一个正确答案，填在题末括号里） 1．由 n 个命题变元组成不等值的命题公式的个数为（ ）。 D B. 2n C. n2 A. 2n D. 2 n2 2.三个命题变元可以构造出彼此不等价的命题公式（ ）个。C D.512 C.256 A. 8 B.64 3. 命题公式  p∨  (q→r)的成假赋值有（ ）个。 A A. 3 B. 4 C. 5 4.命题公式(pq)r的成真赋值有（ ）个。D A. 2 B. 3 C. 4 5. 下列关系式中错误的是（ ）。 B D. 6 D. 5 A. p∧(p∨(r∧s))  p B. p→(q→r)  (p→q)→r C. p∧(p→q )  p∧q D. p∨q  q→p 6. 下列关系式中错误的是（ ）。 D A. p∨q  p→q B. (p→r)∧(q→r)  (p∨q)→r C. (p→r)∧q  (  p∨r)∧q D.  (p  q)  p   q 7. 小项m 011 的表达式是（ ）。D A. p∨  q∨  r C.p∧  q∧  r B.  p∨q∨r D.  p∧q∧r 8. 命题公式(pq)r 的成真赋值为（ A. 001，011，101，110，111 C.全体赋值 ）。A B. D.无 000，001，110 9.下面联结词集合中（ A.{  ，∨} B.{  ，∧} D.{↓} ）不是完备集。 C C.{→} 1
    二、填空题 1. 下列句子中，是命题的有 (1)(3)(5) (1).我是教师。 (2).禁止吸烟！ (3).蚊子是鸟类动物。 (4).上课去！ (5).月亮比地球大。 2. 设 P：我生病，Q：我去学校 (1).命题“我虽然生病但我仍去学校”符号化为 PQ (2).命题“只有在生病的时候，我才不去学校”符号化为 Q P 。 (3).命题“如果我生病，那么我不去学校”符号化为 PQ 。 。 3. 设 P：我有钱，Q：我去看电影。 (1).命题“如果我有钱，那么我就去看电影”符号化为 PQ (2).命题“虽然我有钱，但我不去看电影”符号化为 PQ (3).命题“当且仅当我有钱时，我才去看电影”符号化为 PQ 。 。 。 4. 对于下列各式，是永真式的有(1) (2) (4)。 (1).(P(PQ))Q (2).P(PQ) (3).Q(PQ) (4).(P(PQ))Q (5).(PQ) Q (P(PQ)) RPR。 5. 6. 对于下列各式 7. 命题公式 P(QR)的成真赋值为 111,110,101,100,010 ，成假赋值为 (1).(PQ)(PQ)可化简为 P (2).Q(P(PQ)) 可化简为 QP (3).(PQ)(QP)P 可化简为 P 。 。 。 000,001, 011 。 8. 写出表中各列所定义的命题联结词。 P  Q 1 0 0 0 Q 1 0 1 0 P 1 1 0 0 P  Q 0 1 1 1 9. 两个重言式的析取是 重言式 ，一个重言式与一个矛盾式的析取 是 重言式 。 10. A、B 为两个命题公式，AB 当且仅当 AB 为重言式 ，AB 当且仅当 AB 为重言式 。 11. 设 P、Q 为两个命题公式，德●摩根律可表示为（PQ） PQ ， （PQ） PQ ，吸收律可表示为 P(PQ) P, P (PQ) P 。 12. 公式(PQ) R 的只含联结词，，的等值式为 (PQ) R 13. 在 命 题 演 算 中 ， 一 个 蕴 含 式 与 它 的 。 式 是 等 值 的 ， 它 的 式与它的 是不等值的。 14. 公式PQ 的反换式为 ，逆反式为 。 2
    15. 任意两个不同极小项的合取为 的析取式必为重言（永真） 。 矛盾 （或永假） 式，全体极小项 16. 命题公式(PQ)的主析取范式为 P Q ，主合取范式的编码表 示为 M0M1M3. 17. 已知公式 A(P,Q,R)的主合取范式为 M0M3M5，它的主析取范式为（写 成编码形式） m1 m2 m4 m6 m7 。 18. 命题公式(PQ)的主析取范式为(PQ)(PQ) ，其编码表示为 m1  m2 ，主合取范式的编码表示为 M0 M3 。 19.将公式  p  q 化成只含∧，∨， 3 个联结词的形式为_( p q)(pq)。 20.将公式(p∨q)→r 化成只含∧，∨，  3 个联结词的形式为___ _( p ∨r)  (q∨r)________。 21.已知 A，B 都是含有 3 个变元的命题公式，并且 A，B 的主析取范式分别 为 1    m mmm 5 、 1 m m m m m m  5 0     3 1 2 3 4 m m m m 4   2 3  ， 则 A ∨ B 的 主 析 取 范 式 为 ；  A 的 主 合 取 范 式 为 0 0 M M M M M M  。     1 2 5 3 4 三、判断题 1． 凡陈述句都是命题。（  ） 2．若 A：张明和李红都是是运动员，则A：张明和李红不都是运动员。（  ） 3．语句 3x+5y=0 是一个命题。（  ） 4.（pq）(pq)是重言式。（  ） 5．命题“如果 1+2=3，那么雪是黑的”是真命题。（ ） 6. P(QR))是一个命题公式，其中 P、Q、R 是命题变元。（  ） 7. P(QRQ))是一个命题公式，其中 P、Q、R 是命题变元。（  ） 四、解答题 1.将下列命题符号化 （1）3 不是偶数或 4 不是偶数是不对的。 解：p: 3 是偶数, q: 4 是偶数 命题符号化为：( pq) （2）你和他都不去，我就不去。 解：p: 你去, q:他去 r: 我去 命题符号化为： ( pq)  r 3
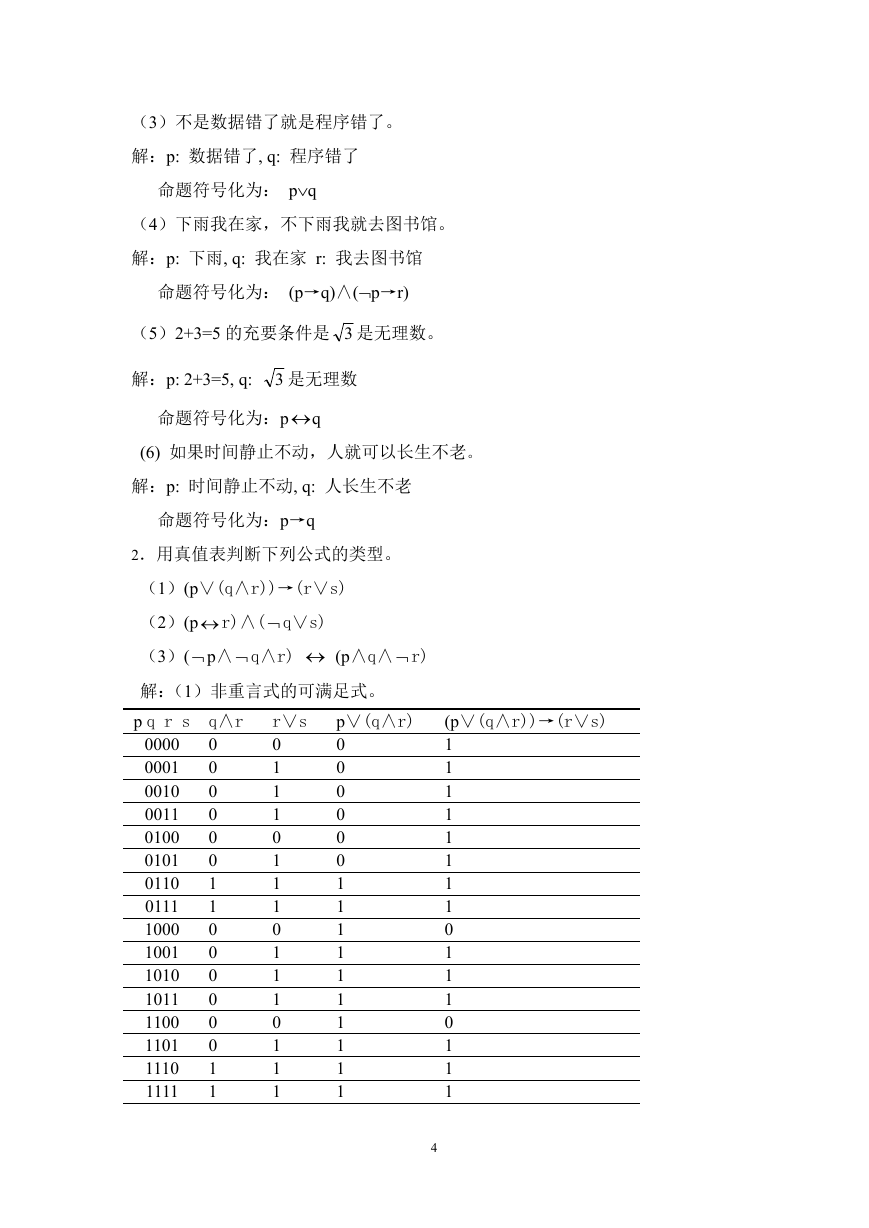
    （3）不是数据错了就是程序错了。 解：p: 数据错了, q: 程序错了 命题符号化为： pq （4）下雨我在家，不下雨我就去图书馆。 解：p: 下雨, q: 我在家 r: 我去图书馆 命题符号化为： (p→q)∧(p→r) （5）2+3=5 的充要条件是 3 是无理数。 解：p: 2+3=5, q: 3 是无理数 命题符号化为：p q (6) 如果时间静止不动，人就可以长生不老。 解：p: 时间静止不动, q: 人长生不老 命题符号化为：p→q 2．用真值表判断下列公式的类型。 （1）(p∨(q∧r))→(r∨s) （2）(p  r)∧(  q∨s) （3）(  p∧  q∧r)  (p∧q∧  r) 解：（1）非重言式的可满足式。 p q r s 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 p∨(q∧r) 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 q∧r 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 r∨s 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 (p∨(q∧r))→(r∨s) 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 4
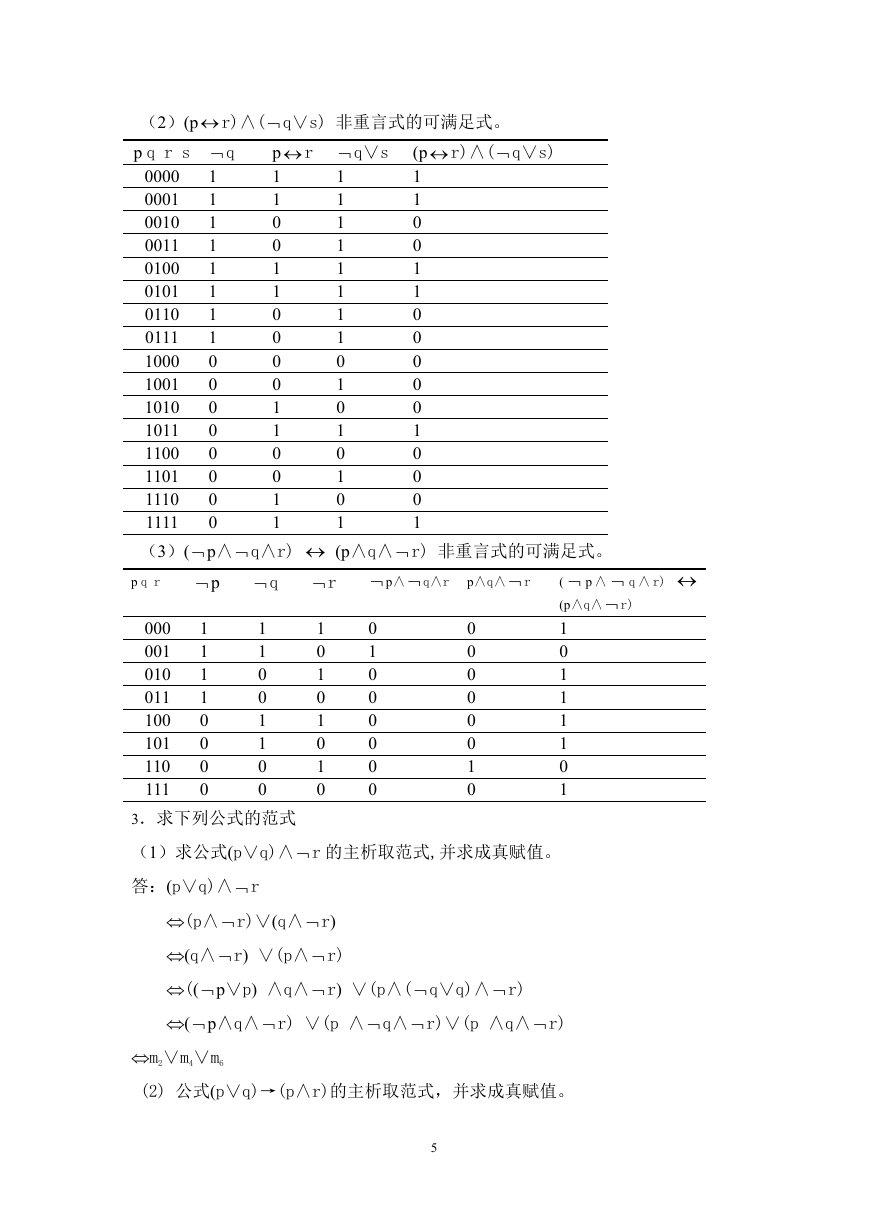
    （2）(p  r)∧(  q∨s) 非重言式的可满足式。 p q r s  q 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 （3）(  p∧  q∧r)  (p∧q∧  r) 非重言式的可满足式。 p q r   p   q   r (p  r)∧(  q∨s) 1 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 p  r  q∨s 1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1  p∧  q∧r p∧q∧  r (  p ∧  q ∧ r)  (p∧q∧  r) 1 0 1 1 1 1 0 1 000 001 010 011 100 101 110 111 1 1 1 1 0 0 0 0 1 1 0 0 1 1 0 0 1 0 1 0 1 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 3．求下列公式的范式 （1）求公式(p∨q)∧  r 的主析取范式,并求成真赋值。 答：(p∨q)∧  r (p∧  r)∨(q∧  r) (q∧  r) ∨(p∧  r) ((  p∨p) ∧q∧  r) ∨(p∧(  q∨q)∧  r) (  p∧q∧  r) ∨(p ∧  q∧  r)∨(p ∧q∧  r) m2∨m4∨m6 (2) 公式(p∨q)→(p∧r)的主析取范式，并求成真赋值。 5
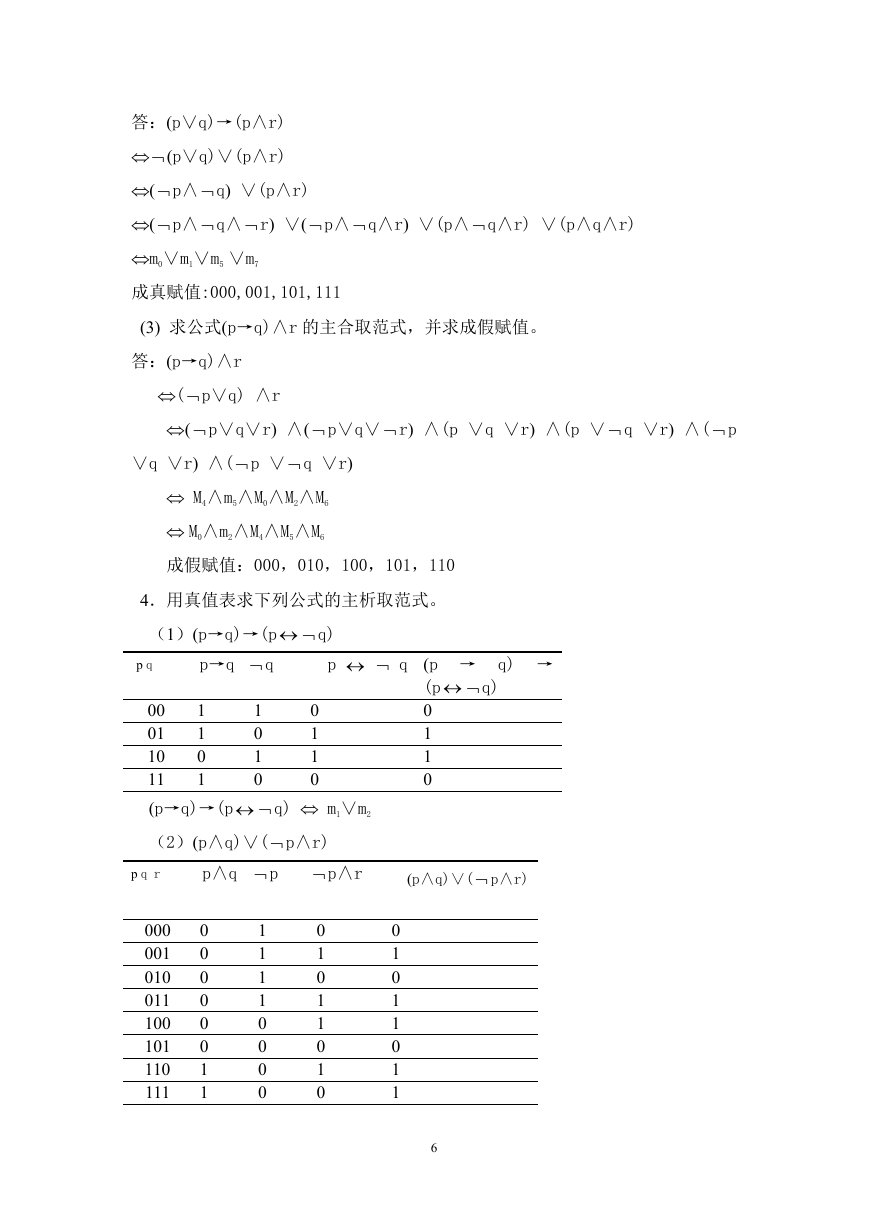
    答：(p∨q)→(p∧r)  (p∨q)∨(p∧r) (  p∧  q) ∨(p∧r) (  p∧  q∧  r) ∨(  p∧  q∧r) ∨(p∧  q∧r) ∨(p∧q∧r) m0∨m1∨m5 ∨m7 成真赋值:000,001,101,111 (3) 求公式(p→q)∧r 的主合取范式，并求成假赋值。 答：(p→q)∧r (  p∨q) ∧r (  p∨q∨r) ∧(  p∨q∨  r) ∧(p ∨q ∨r) ∧(p ∨  q ∨r) ∧(  p ∨q ∨r) ∧(  p ∨  q ∨r)  M4∧m5∧M0∧M2∧M6  M0∧m2∧M4∧M5∧M6 成假赋值：000，010，100，101，110 4．用真值表求下列公式的主析取范式。 （1）(p→q)→(p   q) p q  p→q  q  p   q p q 1 0 1 0 0 1 1 0 1 1 0 1 00 01 10 11 (p→q)→(p   q)  m1∨m2 （2）(p∧q)∨(  p∧r) (p → q) → (p   q) 0 1 1 0 p q r  p∧q  p   p∧r (p∧q)∨(  p∧r) 000 001 010 011 100 101 110 111 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 1 1 6
    (p∧q)∨(  p∧r)  m1∨m3 ∨m4∨m6∨m7 五、证明题 1．用附加前提证明法证明下面推理的正确性。 前提：(pq)r，sp，q 结论：sr 证明：① s 附加前提引入 ② sp 前提引入 ③ p ①②析取三段论 ④ (pq)r 前提引入 ⑤ q ⑥ pq ⑦ r 前提引入 ③⑤合取 ⑥④假言推理 2. 证明下列推理的正确性。 前提：p→  q，  r∨q，r 结论： p 证法1：①p→  q 前提引入 ②  p∨  q ③ q→  p ①置换 ②置换 ④ r∨q 前提引入 ⑤ r→q ④置换 ⑥ r→  p ⑤③假言三段论 ⑦ r ⑧ p 前提引入 ⑥⑦假言推理 由归谬法得推理正确。 7
    证法2：① p 结论的否定引入 ② p→  q 前提引入 ③  q ①②假言推理 ④ r∨q ⑤ r 前提引入 ③④析取三段论 ⑥ r 前提引入 ⑦ r∧ r ⑥⑤合取 由归谬法得推理正确。 3. 证明下列恒等式(p→r)∧(q→r)  (p∨q)→r 证明：利用等值演算 (p→r)∧(q→r)  ( p∨r)∧( q∨r)  （ p∧ q）∨r  (p∨q)∨r  (p∨q)→r 蕴涵等值式 分配律 德●摩根律 蕴涵等值式 4. 在自然推理系统P中构造下面推理的证明： 如果小张守第一垒并且小李向B队投球，则A队将取胜。或者A队未取胜，或者A 队成为联赛第一名。A队没有成为联赛第一名。小张守第一垒。因此，小李没向B 队投球。 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    考试认证

    共收录20637份资料，累计11个分类，关注成员有19位，主要包括：真题,美赛,软考,PMP,Linux/Unix认证,思科认证,微软认证,Oracle认证,华为认证,软考等考,其它

    热门标签

    真题 美赛 软考 PMP Linux/Unix认证 思科认证 微软认证 Oracle认证 华为认证 软考等考 其它

    最新资料