logo资料库

一种二阶动力电池的扩展卡尔曼滤波SOC估计.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.49M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 一种二阶动力电池的扩展卡尔曼滤波 SOC 估计# 陈福熙，皇甫宜耿，卓生荣** （西北工业大学自动化学院,西安 710072） 摘要：为了提高电动汽车的整体性能,延长动力电池的使用寿命,需要一个高效的电池管理系 统。针对锂离子电池存在平台电压导致 SOC 估计难度增大的问题，首先建立电池的二阶等效 电路模型，根据电池的充放电数据，使用曲线拟合的方法，获得相应的参数。基于该模型的 Matlab/Simulink 仿真实验表明，扩展卡尔曼滤波算法在存在 SOC 初始误差及检测噪声的情 况下，也能快速准确地估计电池的 SOC。 关键词：电力电子；动力电池；二阶模型；扩展卡尔曼滤波；SOC 估计 中图分类号：TM912 5 10 15 A Second-order Power Battery SOC Estimation Using Extended Kalman Filter CHEN Fuxi, HUANGFU Yigeng, ZHUO Shengrong (School of Automation ,Northwestern Polytechnical University，Xi'an 710129) 20 25 Abstract: In order to improve the overall performance of electric vehicles and extend battery life, an efficient battery management system is required. because of plateau voltage, It is difficult to estimate SOC because of plateau voltage. Firstly, the battery of second-RC equivalent circuit model is established. The curve fitting method is used to obtain the corresponding parameters which based on a battery charge and discharge data. Simulations based on this circuit model show that the extended Kalman filter algorithm can estimate the SOC of the battery quickly and accurately in the presence of SOC initial error and sense of noise. Key words: Power Electronics; Power battery; second-order model; Extended Kalman filter; SOC estimate 0 引言 近来，随着汽车工业的飞速发展，我国的汽车保有量也逐年递增[1]。然而传统汽车工业 30 在飞速发展的同时，也带来了能源不足和环境污染等一系列不能够被忽视的问题。推广电动 汽车，加快实现由传统能源向新能源转型，是实现汽车工业可持续发展的最佳途径。作为电 动汽车的动力源，动力电池在电动汽车的生产和使用至关重要。为了提高动力电池的性能， 延长其使用寿命，就需要一个高效的电池管理系统（Battery Management System, BMS）。 而电池管理系统的最基本的任务就是要准确估计电池的荷电状态（Stage of Charge, SOC）。 35 目前，并没有一种完美的 SOC 估计方法，国内外常用的 SOC 估计算法主要有一下几种： 安时积分法[2~3]、开路电压法[4]、卡尔曼滤波法[5]等。安时积分法在已知电池初始 SOC 值，并 且电流检测精度高时，能够较为准确地估计 SOC。但在电动汽车中，汽车工作于复杂的环境， 电流变化频繁，电流检测装置不可避免会出现敏感度降低，从而使检测得精度降低。开路电 压法是让电池处于足够长时间的静置状态后，根据电池的开路电压同 SOC 之间的函数关系式 基金项目：教育部博士点新教师基金（20126102120050） 作者简介：陈福熙（1993- ），男，硕士研究生，电源变换技术 通信联系人：皇甫宜耿（1981- ），男，研究生导师，现代新能源发电及电源变换技术，非线性系统鲁棒 控制技术. E-mail: yigeng@nwpu.edu.cn - 1 -
    中国科技论文在线 http://www.paper.edu.cn 40 估计 SOC 的。在实际使用汽车时，不可能让汽车静置足够长的时间，这使得开路电压法的使 用受到限制。卡尔曼滤波法的核心思想就是对系统状态的最优估计。基于选用的电池模型， 选择合理的卡尔曼滤波法估计 SOC。由于在电流频繁变化的场合，卡尔曼滤波算法还能适用， 因此卡尔曼滤波法可以用来估计电动汽车动力电池的 SOC，也是目前使用最多的 SOC 估计方 法。文献[6]使用 UKF 估计电池的 SOC，使用 7 阶多项式方程表示开路电压与 SOC 之间的关系。 45 但 7 阶多项式需要求 8 个参数，计算量大。此外，实验使用的电池并不存在平台电压，而锂 离子电池中却存在平台电压，该文献并没有研究这个问题。 本文在现有的锂离子等效电路模型的基础上，通过充放电实验，对模型的参数进行识别。 采用扩展卡尔曼滤波方法，对锂离子电池的 SOC 进行动态估计。使用 Matlab/Simulink 仿真 不同工况电流时的 SOC 估计，验证算法的有效性。 50 1 等效电路模型与参数识别 为了更加直观准确地描述电池的动静态特性，常使用等效模型来研究实际的电池。在现 有的模型中，等效电路模型因其物理量清晰，数学表达式简单，常为人们使用。常用的等效 电路模型有内阻模型、PNGV 模型和 Thevenin 模型[7~8]等。本论文选用的模型是二阶 RC 等 效电路模型，具有结构简单，计算时间较少等特点。通过现有的文献和实验发现，使用二阶 RC 等效电路模型就能够很好地模拟锂离子电池的特性[9]。模型的电路图如图 1 所示。 55 图 1 二阶 RC 等效电路模型 Fig.1 equivalent circuit model of second-order RC 60 R1、C1 构成时间常数较小的阻容网络，模拟电压的快速变化过程；R2、C2 构成时间常 数较大的阻容网络，模拟电压的缓慢变化过程。R0 为电池的内阻，Uoc 为开路电压，Ul 为电 池的端口电压。其电路方程用式(1)表示。 (1) 要想得到二阶 RC 等效电路模型的参数，需要知道电池的 OCV-SOC 曲线。OCV 即电 池的开路电压，是指电池在不带负载且静置一长段时间（一般为半个小时）后的端口电压， 65 在大多数情况下，一般认为开路电压可以表示电池电动势，所谓 OCV-SOC 曲线就是描述开 路电压与电池荷电深度的关系。选择 OCV-SOC 曲线参数识别的方法，使用不同倍率的恒流 电进行放电实验，记录负载端电压和 SOC 的值。分别选用 1C 和 2C 倍率的电流进行恒流放 电实验， C 代表的是电池充放电时电流的大小与额定容量的比例，即倍率。在本次实验中， 1C 表示放电电流为 6.5A，2C 则代表的是 13A。实验得到的结果如图 2 所示。 - 2 - UocUlR0IlC1R1R2C211111222220121010LLloclIRCUCUUUIRCCUUIRUU
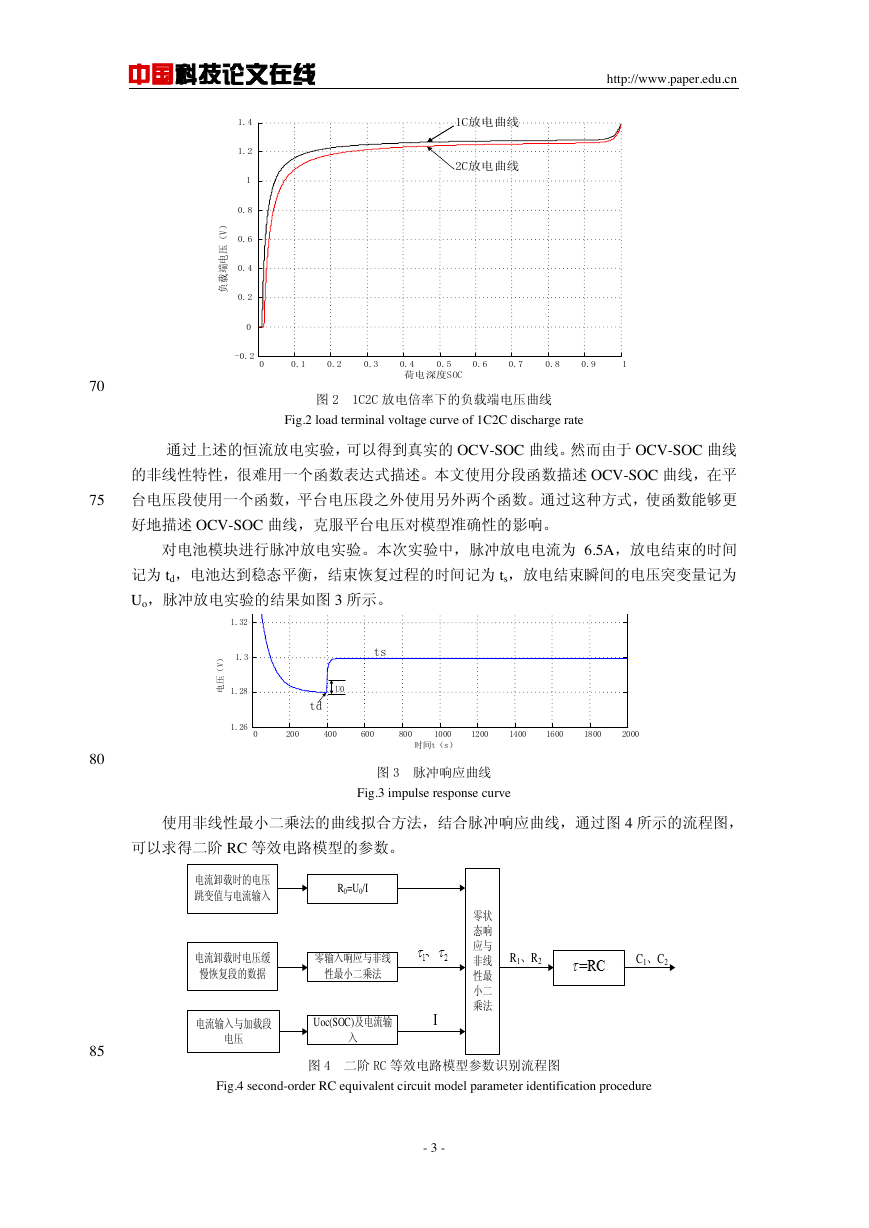
    中国科技论文在线 http://www.paper.edu.cn 70 图 2 1C2C 放电倍率下的负载端电压曲线 Fig.2 load terminal voltage curve of 1C2C discharge rate 通过上述的恒流放电实验，可以得到真实的 OCV-SOC 曲线。然而由于 OCV-SOC 曲线 的非线性特性，很难用一个函数表达式描述。本文使用分段函数描述 OCV-SOC 曲线，在平 75 台电压段使用一个函数，平台电压段之外使用另外两个函数。通过这种方式，使函数能够更 好地描述 OCV-SOC 曲线，克服平台电压对模型准确性的影响。 对电池模块进行脉冲放电实验。本次实验中，脉冲放电电流为 6.5A，放电结束的时间 记为 td，电池达到稳态平衡，结束恢复过程的时间记为 ts，放电结束瞬间的电压突变量记为 Uo，脉冲放电实验的结果如图 3 所示。 80 85 图 3 脉冲响应曲线 Fig.3 impulse response curve 使用非线性最小二乘法的曲线拟合方法，结合脉冲响应曲线，通过图 4 所示的流程图， 可以求得二阶 RC 等效电路模型的参数。 图 4 二阶 RC 等效电路模型参数识别流程图 Fig.4 second-order RC equivalent circuit model parameter identification procedure - 3 - 00.10.20.30.40.50.60.70.80.91-0.200.20.40.60.811.21.4荷电深度SOC负载端电压（V） 1C放电曲线2C放电曲线02004006008001000120014001600180020001.261.281.31.32时间t（s）电压（V） U0tdts 电流卸载时的电压跳变值与电流输入电流卸载时电压缓慢恢复段的数据电流输入与加载段电压R0=U0/I零输入响应与非线性最小二乘法零状态响应与非线性最小二乘法Uoc(SOC)及电流输入R1、R2C1、C2I
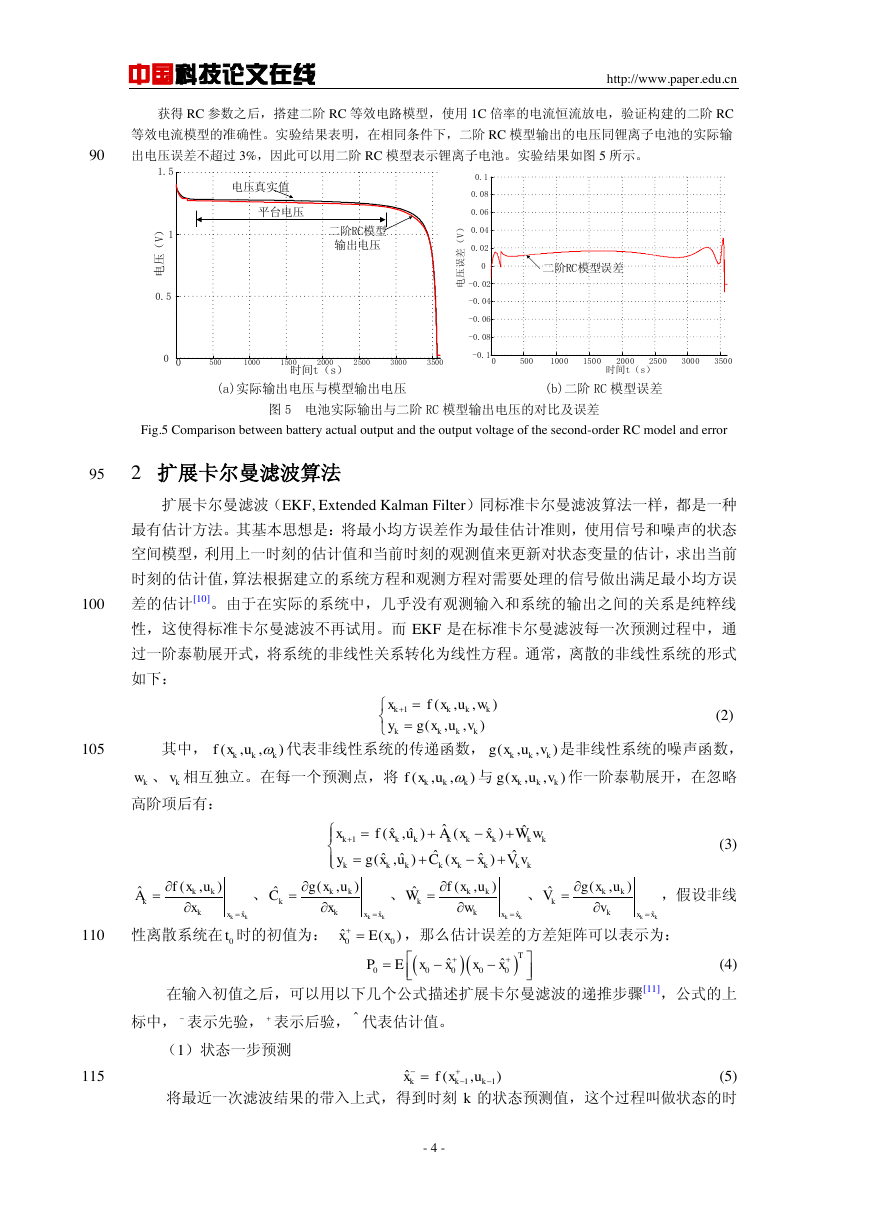
    中国科技论文在线 http://www.paper.edu.cn 获得 RC 参数之后，搭建二阶 RC 等效电路模型，使用 1C 倍率的电流恒流放电，验证构建的二阶 RC 等效电流模型的准确性。实验结果表明，在相同条件下，二阶 RC 模型输出的电压同锂离子电池的实际输 90 出电压误差不超过 3%，因此可以用二阶 RC 模型表示锂离子电池。实验结果如图 5 所示。 (a)实际输出电压与模型输出电压 (b)二阶 RC 模型误差 图 5 电池实际输出与二阶 RC 模型输出电压的对比及误差 Fig.5 Comparison between battery actual output and the output voltage of the second-order RC model and error 95 2 扩展卡尔曼滤波算法 扩展卡尔曼滤波（EKF, Extended Kalman Filter）同标准卡尔曼滤波算法一样，都是一种 最有估计方法。其基本思想是：将最小均方误差作为最佳估计准则，使用信号和噪声的状态 空间模型，利用上一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，求出当前 时刻的估计值，算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误 100 差的估计[10]。由于在实际的系统中，几乎没有观测输入和系统的输出之间的关系是纯粹线 性，这使得标准卡尔曼滤波不再试用。而 EKF 是在标准卡尔曼滤波每一次预测过程中，通 过一阶泰勒展开式，将系统的非线性关系转化为线性方程。通常，离散的非线性系统的形式 如下： 105 其中， 代表非线性系统的传递函数， 是非线性系统的噪声函数， 、 相互独立。在每一个预测点，将 与 作一阶泰勒展开，在忽略 高阶项后有： (2) (3) 、 、 、 ，假设非线 110 性离散系统在 时的初值为： ，那么估计误差的方差矩阵可以表示为： 在输入初值之后，可以用以下几个公式描述扩展卡尔曼滤波的递推步骤[11]，公式的上 (4) 标中， 表示先验， 表示后验， 代表估计值。 （1）状态一步预测 115 (5) 将最近一次滤波结果的带入上式，得到时刻 k 的状态预测值，这个过程叫做状态的时 - 4 - 050010001500200025003000350000.511.5时间t（s）电压（V） 电压真实值二阶RC模型输出电压平台电压0500100015002000250030003500-0.1-0.08-0.06-0.04-0.0200.020.040.060.080.1时间t（s）电压误差（V） 二阶RC模型误差1(,,)(,,)kkkkkkkkxfxuwygxuv(,,)kkkfxu(,,)kkkgxuvkwkv(,,)kkkfxu(,,)kkkgxuv1ˆˆˆˆˆ(,)()ˆˆˆˆˆ(,)()kkkkkkkkkkkkkkkkxfxuAxxWwygxuCxxVvˆ(,)ˆkkkkkkxxfxuAxˆ(,)ˆkkkkkkxxgxuCxˆ(,)ˆkkkkkkxxfxuWwˆ(,)ˆkkkkkkxxgxuVv0t00ˆ()xEx00000ˆˆTPExxxx11ˆ(,)kkkxfxu
    中国科技论文在线 间更新。 （2）估计误差协方差一步预测 120 其中 为 时刻估计误差协方差的先验估计 （3） 时刻最优卡尔曼滤波增益 （4） 时刻状态最优估计 http://www.paper.edu.cn (6) (7) (8) 125 利用状态一步估计得到 ，将其代入到观测方程，得到观测输出 ，把 时刻 系统的实际输出同观测输出作差，将这个差值同 时刻最优卡尔曼滤波增益相乘，得到 时 刻新的估计 ，则可以得到系统 时刻 的最有估计值 。 （5）估计误差协方差最优估计 (9) 130 将本次滤波的结果保留下来，作为下一时刻（ 时刻）的已知量，在求得下一个观测 输出 之后，利用 重复上述步骤。 欲使用 EKF 估计 SOC，需要先将电池的二阶 RC 等效电路模型离散化。令 x1=U1，x2=U2， x3=SOC，设电流 i(t)为系统的输入 u，令放电时刻电流为正号，即 u>0，反之，u<0，系统的 输出是负载上的端电压，即 。根据电池的二阶 RC 等效电路模型，可以写出式(10)所示 135 的电池状态空间模型： (10) f(x)表示的是电池的 OCV 与 SOC 之间的关系。结合本论文使用的等效电路模型，系统 误差的协方差矩阵 Q 和观测噪声的协方差矩阵 R。假设在滤波过程中，k 时刻的最优预测向 量 是已知的，那么可以通过下面的几个步骤推测中在 时刻的状态向量，具体步骤如 140 下： （1）通过式(10)，根据上一时刻的滤波值和输入信号，可以得到系统在 时刻的状 态向量的先验预测值 ，也就是得到电池 SOC 的先验估计值。 （2）通过得到的状态向量的先验预测值 ，可以得到电池端电压的先验估计值 。 （3）在电流检测的过程中引入了系统误差 ，那么估计误差的协方差矩阵的先验估 145 计值为： （4）由式(4.16)求 时刻的最优卡尔曼滤波增益： (11) (12) （5）由测得的实际输出 ，即电池端电压 ，求 SOC 的后验估计值： - 5 - 11ˆˆˆˆTTkkkkkkkPAPAWQWkPkk1ˆˆˆˆˆTTTkkkkkkkkkKPCCPCVPVkˆˆˆ(,)kkkkkkxxKygxuˆkxˆ(,)kkgxukkkˆkxktxˆkxˆkkkkPIKCP1k1kyˆkxlyu1111122222333120110011000001()NRCCxxxxuRCCxxCyfxxxRuˆkx1k1kˆ(1)xk1ˆkx1ˆkykw1111ˆˆTkkkkkPAPAQ1k11111111ˆˆˆTTkkkkkkkKPCCPCRky(1)yk
    中国科技论文在线 150 http://www.paper.edu.cn (13) （6）根据式(9)，更新后验误差协方差矩阵 ，用于下一时刻卡尔曼滤波的递推。 3 仿真验证 扩为了验证扩展卡尔曼滤波算法估计电池 SOC 的准确性，本文分别设计实验，验证电池 在恒流放电和变电流周期放电情况下，估算电池的 SOC，并分析之。为了说明扩展卡尔曼滤 155 波算法的估计值最终会收敛到真实值，本文还设计了分别使用安时积分法与扩展卡尔曼滤波 法，做无初始误差和有初始误差的对比实验。为了有一个参考值，本文选用 Matlab/Simulink 中提供的锂离子电池作为参考对象。 本次实验的电池使用 Matlab 中的锂离子电池，容量为 6.5Ah，分别对电池进行恒流放 电和变电流周期放电，使用扩展卡尔曼滤波算法估计 SOC。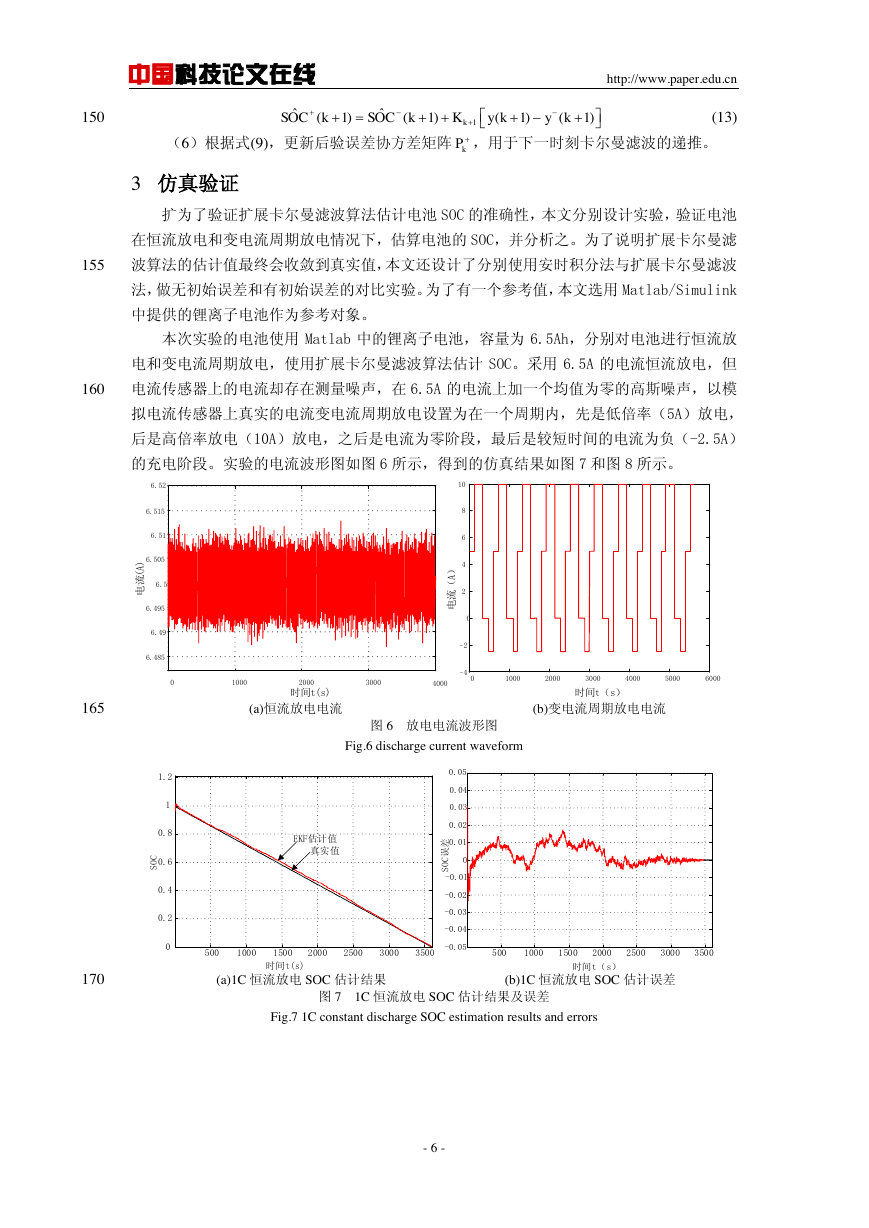采用 6.5A 的电流恒流放电，但 160 电流传感器上的电流却存在测量噪声，在 6.5A 的电流上加一个均值为零的高斯噪声，以模 拟电流传感器上真实的电流变电流周期放电设置为在一个周期内，先是低倍率（5A）放电， 后是高倍率放电（10A）放电，之后是电流为零阶段，最后是较短时间的电流为负（-2.5A） 的充电阶段。实验的电流波形图如图 6 所示，得到的仿真结果如图 7 和图 8 所示。 165 (a)恒流放电电流 (b)变电流周期放电电流 图 6 放电电流波形图 Fig.6 discharge current waveform 170 (a)1C 恒流放电 SOC 估计结果 (b)1C 恒流放电 SOC 估计误差 图 7 1C 恒流放电 SOC 估计结果及误差 Fig.7 1C constant discharge SOC estimation results and errors - 6 - 1ˆˆ(1)(1)(1)(1)kSOCkSOCkKykykkP0100020003000400050006000-4-20246810时间t（s）电流（A）010002000300040006.4856.496.4956.56.5056.516.5156.52时间t(s)电流(A)50010001500200025003000350000.20.40.60.811.2时间t(s)SOC EKF估计值真实值500100015002000250030003500-0.05-0.04-0.03-0.02-0.0100.010.020.030.040.05时间t（s）SOC误差
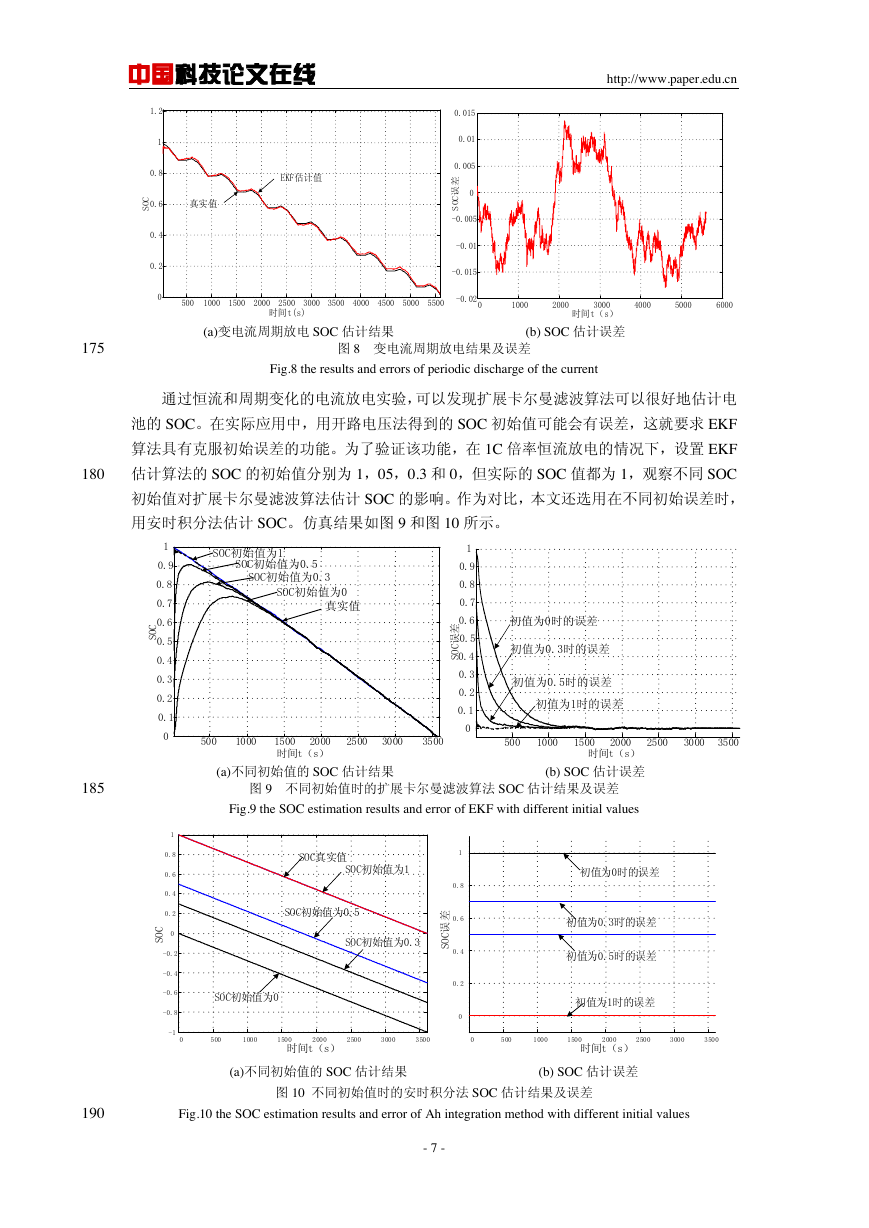
    中国科技论文在线 http://www.paper.edu.cn 175 图 8 变电流周期放电结果及误差 (a)变电流周期放电 SOC 估计结果 (b) SOC 估计误差 Fig.8 the results and errors of periodic discharge of the current 通过恒流和周期变化的电流放电实验，可以发现扩展卡尔曼滤波算法可以很好地估计电 池的 SOC。在实际应用中，用开路电压法得到的 SOC 初始值可能会有误差，这就要求 EKF 算法具有克服初始误差的功能。为了验证该功能，在 1C 倍率恒流放电的情况下，设置 EKF 180 估计算法的 SOC 的初始值分别为 1，05，0.3 和 0，但实际的 SOC 值都为 1，观察不同 SOC 初始值对扩展卡尔曼滤波算法估计 SOC 的影响。作为对比，本文还选用在不同初始误差时， 用安时积分法估计 SOC。仿真结果如图 9 和图 10 所示。 (a)不同初始值的 SOC 估计结果 (b) SOC 估计误差 185 图 9 不同初始值时的扩展卡尔曼滤波算法 SOC 估计结果及误差 Fig.9 the SOC estimation results and error of EKF with different initial values (a)不同初始值的 SOC 估计结果 (b) SOC 估计误差 图 10 不同初始值时的安时积分法 SOC 估计结果及误差 190 Fig.10 the SOC estimation results and error of Ah integration method with different initial values - 7 - 500100015002000250030003500400045005000550000.20.40.60.811.2时间t(s)SOC 真实值EKF估计值0100020003000400050006000-0.02-0.015-0.01-0.00500.0050.010.015时间t（s）SOC误差50010001500200025003000350000.10.20.30.40.50.60.70.80.91时间t（s）SOC 50010001500200025003000350000.10.20.30.40.50.60.70.80.91时间t（s）SOC误差 SOC初始值为0SOC初始值为0.3SOC初始值为0.5SOC初始值为1初值为0时的误差初值为0.3时的误差初值为1时的误差初值为0.5时的误差真实值0500100015002000250030003500-1-0.8-0.6-0.4-0.200.20.40.60.81时间t（s）SOC 050010001500200025003000350000.20.40.60.81时间t（s）SOC误差 SOC真实值SOC初始值为1SOC初始值为0.5SOC初始值为0.3SOC初始值为0初值为1时的误差初值为0.3时的误差初值为0时的误差初值为0.5时的误差
    中国科技论文在线 http://www.paper.edu.cn 通过仿真实验，发现扩展卡尔曼滤波算法估计 SOC 符合实际情况，当电流检测引入观 测噪声时，扩展卡尔曼滤波算法也能准确估计 SOC，具有很好的噪声抑制功能。此外，该 法在存在 SOC 初始误差的情况下，也能使预测值较快地收敛到真实值。因此，可以用扩展 卡尔曼滤波算法估计电池 SOC。 195 4 结论 本文给出了一种基于等效电路模型的 SOC 估计算法，使用曲线拟合的方式，获得等效 电路模型的参数，通过扩展卡尔曼滤波算法估计动力电池的 SOC，克服了平台电压对估计 结果的影响，使得 SOC 的估计误差不超过 2%。通过仿真实验，可以得到如下结论：扩展卡 尔曼滤波算法可以减少在电流电压采样的过程引入的噪声对估计值的影响，大大提高估计的 200 准确性；扩展卡尔曼滤波算法不仅在 SOC 无初始误差时，能够实现 SOC 准确估计，而且在 SOC 存在初始误差时，也能够较快地使估计值收敛到真实值。 [参考文献] (References) 205 210 215 220 [1] 中 华 人 民 共 和 国 国 家 统 计 局 .2014 年 国 民 经 济 和 社 会 发 展 统 计 公 报 [J]. http:/www.stats.gov.cn/tjsj/zxfb/201502/t20150226,2014. [2] 鲍慧,于洋.基于安时积分法的电池 SOC 估算误差校正[J]. 计算机仿真, 2013, 30(11): 148-151. [3] Kong S.N, Chin S.M, Chen Y.P, et al. Enhanced Coulomb Counting Method for Estimating State-of-Charge and State-of-Health of Lithium-ion Batteries [J]. Applied Energy. 2009(86): 1506-1511. [4] 林成涛，陈全世，王军平.用改进的安时计量法估计电动汽车动力电池 SOC[J].清华大学学报( 自然科学 版),2006.46(2):247-251 [5] Xia B, Chen C, Tian Y, et al. A novel method for state of charge estimation of lithium-ion batteries using a nonlinear observer[J]. Journal of Power Sources, 2014, 270: 359-366. [6] Sun F, Hu X, Zou Y, et al. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles[J]. Energy, 2011, 36(5): 3531-3540. [7] Chen M, Rincón-Mora G. Accurate electrical battery model capable of predicting runtime and IV performance[J]. Energy conversion, ieee transactions on, 2006, 21(2): 504-511. [8] Yang Y, TANG T, QIN D, et al. PNGV equivalent circuit model and SOC estimation algorithm of lithium batteries for electric vehicle[J]. Journal of System Simulation, 2012, 4: 041. [9] 董冰. 基于锂离子动力电池的纯电动汽车能量管理系统控制策略与优化[D]. 长春:吉林大学，2014 [10] 彭丁聪. 卡尔曼滤波的基本原理及应用[J]. 软件导刊, 2009, 11:011. [11] Zhu Z, Sun W J, Rong Y, et al. SOC EKF Estimation Based on a Second-order LiFePO4 Battery Model[J]. TELKOMNIKA Indonesian Journal of Electrical Engineering, 2013, 11(8): 4208-4213. - 8 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料