第1页 / 共4页
第2页 / 共4页
第3页 / 共4页
第4页 / 共4页
2019年湖北武汉科技大学交通运输系统工程考研真题及答案.doc
2019 年湖北武汉科技大学交通运输系统工程考研真题及答
案
一、（30 分）用大 M 求解线性规划问题。
min
z
x
3
x
3
,
0
6
x
1
1
1
5
x
x
x
2
2
2
x
1
x
3
2
x
2
x
x
,
0
5
x
3
3
2
4
4
10
0
3
二、（30 分）分配 P1~P4 四人去完成 A、B、C、D、E 五项任务，每人完成各项任务的费用如
表 1 所示。由于任务重，人数少，因此考虑任务 E 必须完成，其他 4 项任务可以完成 3 项，
但由于任务 A 的特殊性，该任务不能由 P1 完成。试问该如何分配，完成任务的总费用最小。
P1
P2
P3
P4
A
75
89
84
74
表 1
C
31
76
78
86
B
79
88
77
92
D
92
70
90
73
E
87
83
82
95
三、（25 分）某产品四个产地的产量需要分别销往 5 个城市，产地到城市间的单位运价以及
产地产量、城市需求量如表 2 所示，由于产地丁与城市 D 间的道路正在维修，因此该地的产
品不能运往城市 D。求运费最小的产品调运方案。
甲
乙
丙
丁
销量
A
10
5
15
20
20
B
2
10
5
15
20
表 2
C
3
15
14
13
30
D
15
2
7
—
10
E
9
4
15
8
25
产量
25
30
20
30
四、（15 分）某公司要在该市的三个片区内建加气站，拟投入的资金最大值为 B 元。现有 A1~A8
共 8 个规划点可供选择。加气站建设时需要考虑的条件是：
在南片区，在 A1，A2，A3 三个点中最多建立两个，
在东片区，在 A4，A5 两个点中至少建一个；
在北片区，在 A6，A7，A8 三个点中最少建立两个；
每个拟建点建加气站的投资为 bi 元，建成后的收益为 ci 元，如何建设加气站，使获利最高。
（只写出模型，不需求解。）
五、（20 分）高速路上设置 1 个临时检查点对车辆进行临时检查，汽车按泊松流到达，达到
率为 80 辆/小时；每辆车的平均检查时间为 30 秒，服从负指数分布，求该系统内有大于 3
辆车的概率以及系统的各项评价指标。
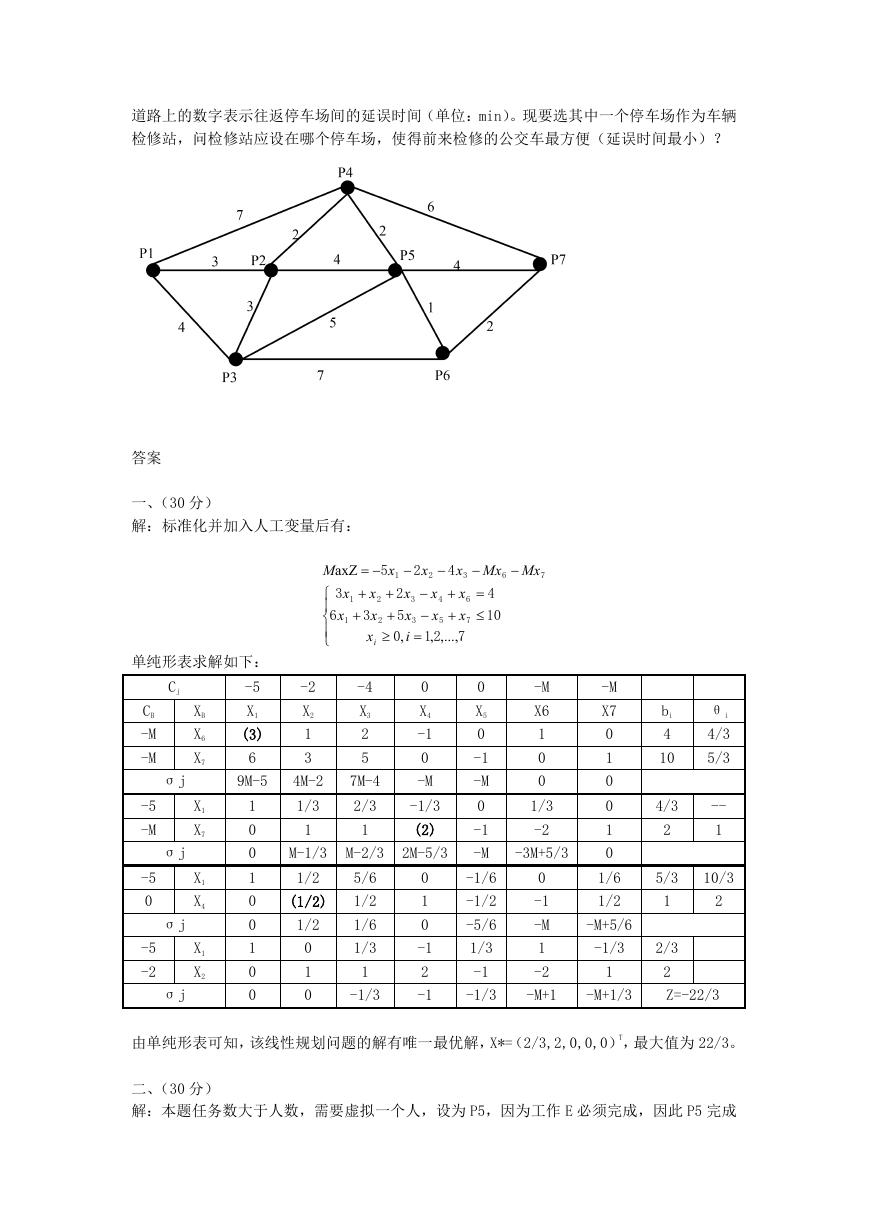
六、（30 分）。某城市有 7 个公交停车场供公交车停放，停车场间的道路如图 1 所示，其中
道路上的数字表示往返停车场间的延误时间（单位：min）。现要选其中一个停车场作为车辆
检修站，问检修站应设在哪个停车场，使得前来检修的公交车最方便（延误时间最小）？
答案
一、（30 分）
解：标准化并加入人工变量后有：
1
axZ
M
x
3
x
6
x
5
1
x
x
2
x
x
5
3
,
x
i
0
2
1
2
i
3
2
4
x
2
x
x
5
,
21
x
4
x
x
,...,
7
3
3
Mx
7
6
Mx
4
10
6
7
单纯形表求解如下：
CB
-M
-M
-5
-M
-5
0
-5
-2
Cj
σj
σj
σj
σj
XB
X6
X7
X1
X7
X1
X4
X1
X2
-5
X1
(3)
6
-2
X2
1
3
-4
X3
2
5
9M-5
4M-2
7M-4
0
X4
-1
0
-M
1
0
0
1
0
0
1
0
0
1/3
1
2/3
1
-1/3
(2)
M-1/3
M-2/3
2M-5/3
1/2
(1/2)
1/2
0
1
0
5/6
1/2
1/6
1/3
1
-1/3
0
1
0
-1
2
-1
0
X5
0
-1
-M
0
-1
-M
-1/6
-1/2
-5/6
1/3
-1
-M
X6
1
0
0
1/3
-2
-3M+5/3
-M
X7
0
1
0
0
1
0
0
-1
-M
1
-2
1/6
1/2
-M+5/6
-1/3
1
bi
4
10
4/3
2
θi
4/3
5/3
--
1
5/3
10/3
1
2
2/3
2
-1/3
-M+1
-M+1/3
Z=-22/3
由单纯形表可知，该线性规划问题的解有唯一最优解，X*=（2/3,2,0,0,0）T，最大值为 22/3。
二、（30 分）
解：本题任务数大于人数，需要虚拟一个人，设为 P5，因为工作 E 必须完成，因此 P5 完成
工作 E 的费用为 M（M 为一非常大的数，代表完成该项任务费用费用高），即 P5 不能完成工
作 E，P5 完成其他工作的费用为 0，同时，由于 P1 不能完成 A，因此，也需要将 P1 完成工
作 A 的费用重新设置为 M，则建立效率矩阵如下：
´
C
0
M
89
84
74
0
79
88
77
92
0
81
76
78
86
0
92
70
90
73
0
87
83
82
95
M
先行变换，然后列变换为
M
19
7
1
0
0
18
0
2
6
1
19
13
0
0
2
C
5 个独立 0 元素，最终效率矩阵为
13
0
13
0
0
M
18
7
][
0
0
3
8
0
17
M
][
0
17
0
18
0
，找独立 0 元素，并进行调整，最后找到
2
5
1
12
][
0
13
][
0
14
0
1
3
7
][
0
16
M
任务分配为：P1→B,P2→D,P3→E,P4→A，任务 C 不完成。
完成任务的最小费用为：79+70+82+74=305
三、（25 分）
解：将丁→D 的运费用 M（无穷大）表示，说明丁的产品不能销往城市 D。用表上作业法求
解为：
A
B
C
E
产量
ui
-6
0
-3
4
9
4
15
8
25
30
20
30
105
甲
乙
丙
丁
11
(20)
13
11
销量
vj
20
5
10
5
15
20
(0)
2
(20)
2
10
5
15
(25)
6
8
3
15
14
13
D
15
19
(10)
8
11
(0)
14
2
7
M
3
(5)
20
8
30
9
(25)
25
4
10
2
最优方案对应的运费为 20×5+20×5+5×13+25×3+10×2+25×8+0×4+0×2=560
四、（15 分）
解：引入 0-1 变量，假设
xi
1
0
点建加气站
Ai
表示在
i
A
点不建加气站
表示
ax
ZM
8
i
1
xc
i
i
x
i
则有：
..
tS
五、（20 分）
8
i
2
bx
i
i
1
x
x
x
x
7
,
i
1或0
4
5
x
1
6
x
B
3
2
x
x
1
2
8
,
,...
821
解：λ=80 辆/小时，μ=60×60÷30=120 辆/小时，则
80
120
.
0
667
系统内多于 3 辆车的概率：
NP
3
4
.(
0
667
4
)
0.196
队长
L
=2（辆）
80
120
2
80
80
)
80
80
qL
W
qW
)
(
1
(
120
1
120
80
)
(
=1.33（辆）
120
=0.025（时）
120
1
(
120
80
)
=0.00021（时）
六、（30 分）
解：先采用距离矩阵法计算出任意两点间的最短距离：
P1
P2
P3
P4
P5
P6
P1
P2
P3
P4
P5
P6
P7
0
3
4
5
7
8
10
3
0
3
2
4
5
7
4
3
0
5
5
6
8
5
2
5
0
2
3
5
7
4
5
2
0
1
3
8
5
6
3
1
0
2
P7
10
7
8
5
3
2
0
10
7
8
5
7
8
10
37
24
31
22
22
25
35
由上表可以看出，公交车检修站可以设置在停车场 P4，不但各停车场到检修站的最大延误
时间最小仅为 5min，同时检修站到其他停车场的延误时间的总和也最小，为 22min。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
