2 王 　波 ,王万良 ,杨旭华 (浙江工业大学 信息工程学院 ,浙江 杭州 310032) 摘要 :对 WS 小世界网络和 N W 小世界网络两种网络模型进行计算机建模 ,并分析它们的静态网 络统计量 ,包括节点的度分布 、平均最短路径和聚类系数等特征指标. 进一步得到了 WS 和 N W 小 世界网络模型的度分布图以及 N W 小世界网络模型的平均最短路径和平均聚类系数的归一化图. 使用 Matlab 软件 ,用邻接矩阵表示网络连接 ,用随机数产生器产生概率 ,生成两种小世界模型. 并 且使用稀疏矩阵的方法 ,大大减少了内存的使用量 ,使仿真程序能生成具有更多网络节点的大型网 络 ,使对数十万节点的网络进行建模和分析成为可能. 关键词 :小世界网络 ;度分布 ;平均最短路径 ;聚类系数 ;稀疏矩阵 中图分类号 :N945. 12 　　　　　文献标识码 :A 文章编号 :1006 4303 (2009) 02 0179 04 2 2 第 37 卷第 2 期 2009 年 4 月 浙 江 工 业 大 学 学 报 J OU RNAL O F ZH EJ IAN G UN IV ERSIT Y O F TEC HNOLO GY Vol. 37 No. 2 Ap r. 2009 WS 与 N W 两种小世界网络模型的建模及仿真研究 Research of modeling and simulation on WS and NW small world network model WAN G Bo , WAN G Wan liang , YAN G Xu hua (College of Information Engineering , Zhejiang University of Technology , Hangzhou 310032 , China) Abstract : The WS and N W small world network are modeled and t he static network statistics are analyzed , including t he degree dist ribution of t he vertex , average shortest pat hs and clustering coefficient . Furt hermore , t he degree dist ribution figures of WS and N W small world network , t he average shortest pat hs , and t he normalized map of average clustering coefficient are obtained. The two small in which t he network connectio ns are p resented wit h adjacency mat rix , t he p robability is generated by random number generator. Meanwhile , t he sparse mat rix is used and it greatly reduces t he memory space. The simulation p rogram can p roduce larger scale networks wit h more vertices. It is po ssible to model and analyze t he networks containing hundreds t housand vertices wit h t his simulation. world networks are modeled using Matlab simulator , Key words : small world network ; degree dist ribution ; average shortest pat hs ; clustering coefficient ; sparse mat rix 0 　引 　言 近年来 ,复杂网络的研究受到了科学和工程各 个领域研究人员的广泛关注 ,复杂网络理论研究也 不再局限于数学领域. 人们开始考虑节点数量众多 、 连接结构复杂的实际网络的整体特性 ,在从物理学 到生物学的众多学科中掀起了研究复杂网络的热 潮 ,甚至于被称为“网络的新科学”[ 1 2 ] . 复杂网络中 小世界网络模型的研究是进行的比较早也是比较多 22 04 收稿日期 :2008 基金项目 :国家自然科学基金资助项目 (60504027 ,60874080) ;中国博士后科学基金资助项目 (20060401037) 作者简介 :王 　波 (1982 —) ,男 ,浙江义乌人 ,博士生 ,研究方向为复杂网络和智能交通. 

·081· 浙 江 工 业 大 学 学 报 第 37 卷 的 ,小世界网络模型包括 WS 小世界网络模型[ 1 ] 、 N W 小世界网络模型[ 3 ] 、Monasson 小世界网络模 型[ 4 ] 以及一些其它的变形模型包括 BW 小世界网络 模型等等[ 5 ] . 其中 Watt s 和 St rogatz 开创性的提出 了小世界网络并给出了 WS 小世界网络模型 ;接着 Newman 和 Watt s 又对 WS 小世界网络模型进行改 进 ,提出了 N W 小世界网络模型 ,他们用随机化加 边代替了随机化重连 ,从而避免了产生孤立节点的 可能. 因此 WS 和 N W 小世界网络模型是最为经典 的小世界网络模型. 所以对 WS 和 N W 小世界网络 模型进行研究是很有意义的. 笔者主要对 WS 小世 界网络 、N W 小 世 界 网 络 进 行 计 算 机 建 模 , 并 用 Matlab 软件进行仿真实现 ,得到它们的静态网络统 计量 ,包括节点的度分布 ( degree dist ribution) 、平 均最 短 路 径 ( average shortest pat hs) 、聚 类 系 数 (clustering coefficient) . 其中对两个小世界网络模 型的 matlab 实现方法做了较详细的介绍 ,并且使用 了稀疏矩阵的方法 ,使得可以生成并分析具有更多 网络节点的小世界网络模型. 1 　网络统计量 复杂网络统计量主要包括度和度分布 、平均最 短路径 、聚类系数等等 ,这些统计量可以深刻的揭露 网络的内部特性 ,下面先分别对这些统计量做简单 的介绍. 1. 1 　度与度分布 度 (degree) 是单独节点的属性中简单而又重要 的概念. 节点的度是指与该节点相关联的边的条数 , 也就是指与该节点连接的其它节点的数目. 度分布 (degree dist ribution) 是指网络中各节点具有的度 的分布 , 一般记作 p ( k) . p ( k) 也等于在随机一致的 原则下挑选出的节点其度数为 k 的概率[6 ] . 1. 2 　平均最短路径 网络的平均最短路径 (average shortest pat hs) 可以对网络的连通性进行较好地描述. 网络中两个 节点 i和 j 之间的距离 d i , j 定义为连接这两个节点的 最短路径上的边数. 网络的平均最短路径长度 L 定 义为任意两点之间的最短路径的平均值 ,即 1 N ( N - 1) L = 1 2 其中 N 为网络的节点数. ∑ i > j d i , j 1. 3 　聚类系数 聚类系数 (clustering coefficient) 表征的是网络 的聚类特性 ,也就是群落特性. 一般假设网络中的节 点 i 与 k i 条边关联 ,即与另外 ki 个节点相连. 显然 , 在这 ki 个节点之间最多可能有 k i ( ki - 1) / 2 条边. 而 这 ki 个节点之间实际存在的边数是 E i . 那么这 ki 个 节点之间实际存在的边数是 Ei 与总的可能的边数 k i ( ki - 1) / 2 之比就定义为节点 i 的聚类系数 C i ,即 Ci = 2 Ei k i ( ki - 1) 而对网络中所有节点的聚类系数取平均值 , 就是整 个网络的聚类系数 C ,即 C = 1 N N ∑ Ci i = 1 其中 N 为网络的节点数. 2 　WS 小世界网络 1998 年 ,Watt s 和 St rogatz 提出了小世界网络 这一概念 ,并建立了 WS 模型[ 1 ] . 实证结果表明 ,大 多数的真实网络都具有小世界特性 (较小的最短路 径) 和聚类特性 (较大的聚类系数) . 传统的规则最 近邻耦合网络具有高聚类的特性 ,但并不具有小世 界特性 ;而 ER 随机网络[ 7 ] 具有小世界特性但却没 有高聚类特性. 因此这两种传统的网络模型都不能 很好的来表示实际的真实网络. Watt s 和 St rogatz 建立的 WS 小世界网络模型就介于这两种网络之 间 ,同时具有小世界特性和聚类特性 ,可以很好的来 表示真实网络. WS 小世界网络模型从规则图开始 : 考虑一个 含有 N 个节点的最近邻耦合网络 , 它们围成一个 环 ,其中每个节点都与它左右相邻的各 k/ 2 个节点 相连 , k 是偶数 , 也就是节点的度 ; 然后进行随机化 重连 :以概率 p 随机地重新连接网络中的每个边 ,即 将边的一个端点保持不变 , 而另一个端点取为网络 中随机选择的一个节点. 并且规定任意两个不同节 点之间至多只能有一条边 , 每一个节点都不能有边 与自身相连. 在 WS 小世界网络模型中 , p = 0 对应于完全规 则网络 , p = 1 则对应于完全随机的网络 ,通过调节 p 的值可以控制从完全规则网络到完全随机网络的 过渡 ,如图 1 所示. 

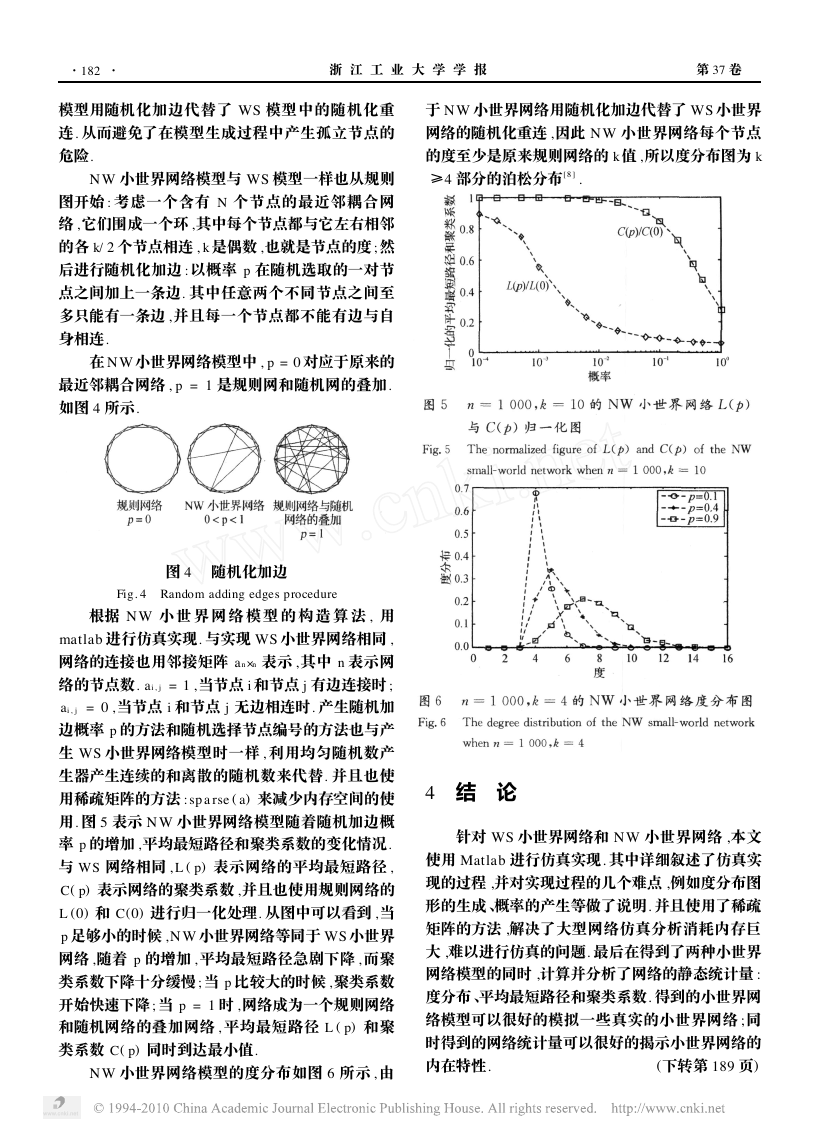
第 2 期 王 　波 ,等 :WS 与 NW 两种小世界网络模型的建模及仿真研究 ·181· 布图形 ,取了其中概率 p 为 0. 1 ,0. 4 ,0. 9 时的度分 布情况. 从图 3 中可以看出 WS 小世界网络的度分 布类似 ER 随机图的度分布 , 服从泊松分布. WS 小 世界模型很好的描述了一个同时具有小世界特性和 高聚类特性的网络 , 但是 WS 网络模型的随机化重 连过程可能会破坏网络的连通性 , 即可能会出现孤 立的节点. 孤立节点的出现会使此节点与其他节点 的最短路径变成无穷大 , 对平均最短路径造成较大 的影响. 一般来说我们可以在计算平均最短路径时 去除这个节点 ,这样对整个网络来说是可取的. 或者 我们也可以用调和平均最短路径来代替平均最短 路径. 3 　NW 小世界网络 由于 WS 小世界网络可能在生成过程中产生孤 立节点 , 不利于对网络特性的分析 , 因此 Newman 和 Watt s 进一步提出了 N W 小世界网络模型[3 ] , 该 图 1 　随机化重连 Fig. 1 　Random rewiring p rocedure 　　根据以上算法使用 matlab 进行仿真 ,网络的连 接用邻接矩阵 an×n 表示 ,其中 n 表示网络的节点数. ai , j = 1 ,当节点 i 和节点 j 有边连接时 ; ai , j = 0 ,当节 点 i 和节点 j 无边相连时. 由规则网络向小世界网络 演化的过程中需要根据概率 p 来决定一条边是否重 连 ,这里的 p 可以由一个均匀连续随机数产生器产 生一个 0 到 1 之间的随机数来代替. 例如假设要以 概率 0. 1 随机重连 ,那么只要产生一个 0 到 1 之间的 随机数σ,当σ< 0. 1 时进行随机重连就可以了. 随机 重连的过程中还需要在整个网络中随机的选择重连 的端点 ,这可以由均匀离散随机数产生器来完成. 产 生一个由 1 到 n的整数随机数 m , m 就代表随机重连 选择到的端点编号 ,当然若 m 恰好等于原端点的编 号 ,就应该再选择一次 , 即再产生一个随机数. 由于 需要存储每一对网络节点之间的边连接情况 , 所以 用来存储一个网络需要的内存量很大. 因此无法对 具有上万个节点的小世界网络进行仿真 , 但是对一 个网络进行仿真分析 ,它的节点数越多 ,那么得到网 络以及统计规律就越具有普遍性 , 越能表现其内部 特征 ,并且真实网络所具有的节点数往往都是很大 的. 所以这里我们使用稀疏矩阵的方法 :sp arse ( a) , 因为小世界网络之间的连接其实是很稀疏的 , 表现 在邻接矩阵上就是矩阵中大部分位置的值是 0 , 只 有小部分的位置是 1. 使用稀疏矩阵的方法可以节 省大量的内存空间 , 使我们可以产生和分析具有数 万以至数十万节点的小世界网络模型. 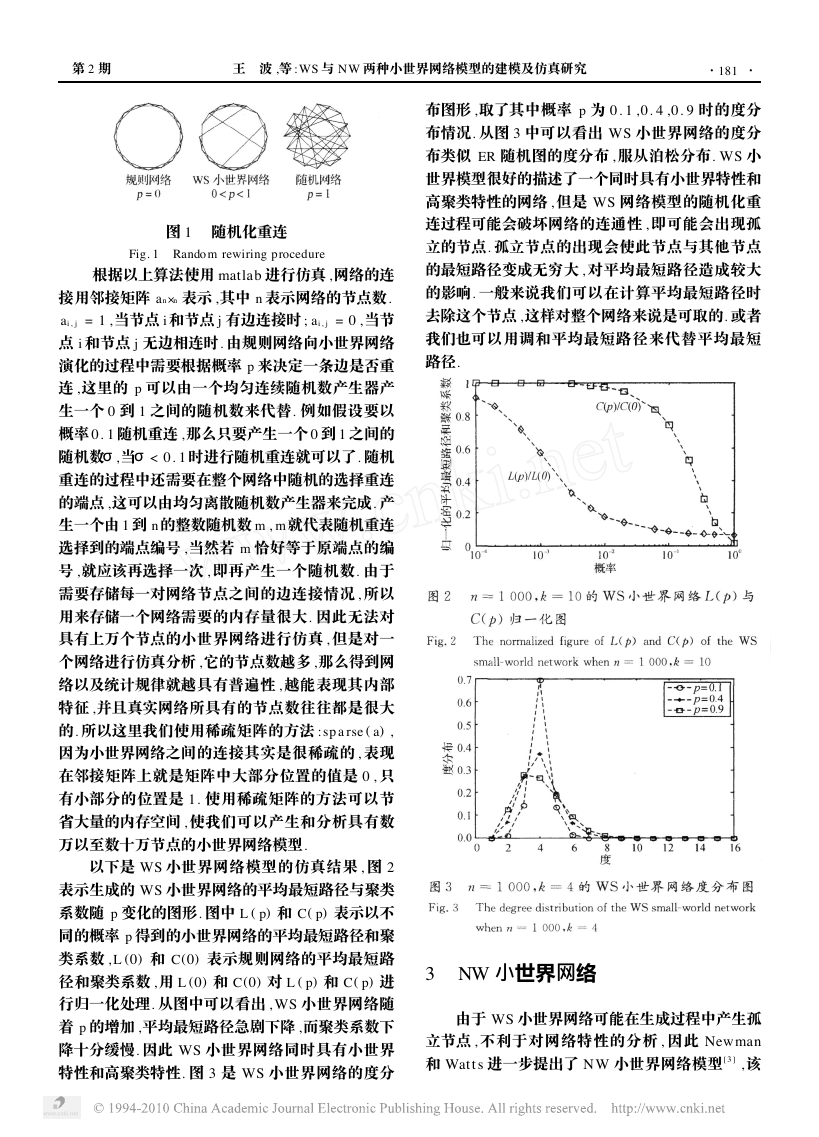以下是 WS 小世界网络模型的仿真结果 , 图 2 表示生成的 WS 小世界网络的平均最短路径与聚类 系数随 p 变化的图形. 图中 L ( p) 和 C( p) 表示以不 同的概率 p 得到的小世界网络的平均最短路径和聚 类系数 , L (0) 和 C(0) 表示规则网络的平均最短路 径和聚类系数 ,用 L (0) 和 C(0) 对 L ( p) 和 C( p) 进 行归一化处理. 从图中可以看出 , WS 小世界网络随 着 p 的增加 ,平均最短路径急剧下降 ,而聚类系数下 降十分缓慢. 因此 WS 小世界网络同时具有小世界 特性和高聚类特性. 图 3 是 WS 小世界网络的度分 

·281· 浙 江 工 业 大 学 学 报 第 37 卷 模型用随机化加边代替了 WS 模型中的随机化重 连. 从而避免了在模型生成过程中产生孤立节点的 危险. N W 小世界网络模型与 WS 模型一样也从规则 图开始 : 考虑一个含有 N 个节点的最近邻耦合网 络 ,它们围成一个环 ,其中每个节点都与它左右相邻 的各 k/ 2 个节点相连 , k 是偶数 ,也就是节点的度 ;然 后进行随机化加边 :以概率 p 在随机选取的一对节 点之间加上一条边. 其中任意两个不同节点之间至 多只能有一条边 ,并且每一个节点都不能有边与自 身相连. 在 N W 小世界网络模型中 , p = 0 对应于原来的 最近邻耦合网络 , p = 1 是规则网和随机网的叠加. 如图 4 所示. 图 4 　随机化加边 Fig. 4 　Random adding edges procedure 根据 N W 小 世 界 网 络 模 型 的 构 造 算 法 , 用 matlab 进行仿真实现. 与实现 WS 小世界网络相同 , 网络的连接也用邻接矩阵 an×n 表示 , 其中 n 表示网 络的节点数. ai , j = 1 ,当节点 i 和节点 j 有边连接时 ; ai , j = 0 ,当节点 i 和节点 j 无边相连时. 产生随机加 边概率 p 的方法和随机选择节点编号的方法也与产 生 WS 小世界网络模型时一样 , 利用均匀随机数产 生器产生连续的和离散的随机数来代替. 并且也使 用稀疏矩阵的方法 :sp arse ( a) 来减少内存空间的使 用. 图 5 表示 N W 小世界网络模型随着随机加边概 率 p 的增加 ,平均最短路径和聚类系数的变化情况. 与 W S 网络相同 , L ( p) 表示网络的平均最短路径 , C( p) 表示网络的聚类系数 ,并且也使用规则网络的 L (0) 和 C(0) 进行归一化处理. 从图中可以看到 ,当 p 足够小的时候 , N W 小世界网络等同于 WS 小世界 网络 ,随着 p 的增加 , 平均最短路径急剧下降 , 而聚 类系数下降十分缓慢 ;当 p 比较大的时候 ,聚类系数 开始快速下降 ;当 p = 1 时 ,网络成为一个规则网络 和随机网络的叠加网络 , 平均最短路径 L ( p) 和聚 类系数 C( p) 同时到达最小值. N W 小世界网络模型的度分布如图 6 所示 , 由 于 N W 小世界网络用随机化加边代替了 WS 小世界 网络的随机化重连 ,因此 N W 小世界网络每个节点 的度至少是原来规则网络的 k 值 ,所以度分布图为 k ≥4 部分的泊松分布[8 ] . 4 　结 　论 针对 WS 小世界网络和 N W 小世界网络 ,本文 使用 Matlab 进行仿真实现. 其中详细叙述了仿真实 现的过程 ,并对实现过程的几个难点 ,例如度分布图 形的生成 、概率的产生等做了说明. 并且使用了稀疏 矩阵的方法 ,解决了大型网络仿真分析消耗内存巨 大 ,难以进行仿真的问题. 最后在得到了两种小世界 网络模型的同时 ,计算并分析了网络的静态统计量 : 度分布 、平均最短路径和聚类系数. 得到的小世界网 络模型可以很好的模拟一些真实的小世界网络 ;同 时得到的网络统计量可以很好的揭示小世界网络的 (下转第 189 页) 内在特性. 

2 2 2 2 2 2 2 2 2 2 第 2 期 2 2 张 　琦 ,等 :多目标出卷系统及其核心算法的研究与设计 ·981· 模块 2 :对模块 1 的转化结果就是各难度分数 取整. 模块 3 :按 4. 1. 2 方法 ,通过在试题库与知识库 中读取各试题的解题时间及其内容类别与题型类别 的参数 ,计算各试题的权重. 模块 4 :按模块 3 计算出各题的权重对各难度 档中的试题进行赋分. 试题分数 = 难度档分数 ×试 题的权重. 模块 5 :对各试题的分数进行取整. 6 　结 　论 出卷系统的研究对开发的软硬件环境要求较 低 、Windows XP 下用 VisualC + + 6. 0 语言实现出 卷算法功能 ,用 M FC 实现用户界面 ,以 Office 软件 输出成卷即可实现系统功能. 开发人员和设备投入 少 ,使用方便 ,具备理论和实际操作上的可行性. 系统设计完成后我们分别进行了系统测试和算 法测试. 算法测试中我们对“难度 —时间”、“内容 — 时间”和“题型 —时间”三个对应关系测试了理论出 卷的符合度 、并对整卷内容覆盖率和出卷效果进行 了检验 ;系统测试中通过操作正确性校验测试 、系统 流程测试 、强度测试三个阶段对整个系统进行了测 试 ,测试结果是有关操作都能正确执行. 根据验证测 试信息 ,发现该出卷系统以下方面需要进一步完善. (1) 在数据库题量不足的情况下 ,选题无法结 束. 解决方法 :设置最大循环次数. (2) 在少数 (几个) 不合理的选题指标下出卷效 果不佳. 解决方法 :对这几个选题指标做特殊处理 , 强行优化. 另外 ,笔者在出卷理论上只研究了”难度 —时 间”、“内容 —时间”、“题型 —时间”三个对应关系 ,对 其他可能与 出卷 有关 的对应 关 系 还 有 待 进 一 步 研究. 参考文献 : [ 1 ] 　姚碧芬. 基于动态评价函数的试卷自动生成系统的设计与实现 [J ] . 现代计算机 ,2006 (9) :83 87. [ 2 ] 　陆蓓 ,王小华. 基于动态多目标评价函数的试卷自动生成策略 [J ] . 杭州电子工业学院学报 ,2002 (1) :11 15. [ 3 ] 　毛秉毅. 基于目标树的组卷算法的研究[J ] . 计算机工程与应 用 ,2002 ,23 :245 247. [ 4 ] 　田翔 ,肖人岳. 一个改进的通用成卷模型[J ] . 计算机工程 ,2004 (19) :187 189. [ 5 ] 　谢平. 基于框架模式的试题库智能组卷系统[J ] . 华东交通大学 学报 ,1998 (4) :60 65. [ 6 ] 　L YNDA T , CHRISMEN T C , MO HAND B. Multiple query Informa evaluation based on enhanced genetic algorit hm [J ] . tion Processing and Management ,2003 ,39 (2) :215 231. (责任编辑 :翁爱湘) (上接第 182 页) 参考文献 : [ 1 ] 　WA T TS D J , STRO GA TZ S H. Collective dynamics of world’networks [ J ] . Nat ure , 1998 , 393 ( 6684 ) : 440 ‘small 442. [ 2 ] 　BARABASI A L , ALBER T R. Emergence of scaling in ran dom net work[J ] . Science ,1999 ,286 (5439) :509 512. [ 3 ] 　N EWMAN M E J , WA T TS D J . Renormalization group anal world network model [J ] . Phys Lett A ,1999 , ysis of t he small 263 :341 346. [ 4 ] 　N EWMAN M E J . The st ruct ure and f unction of complex net works[J ] . SIAM Review ,2003 ,45 :167 256. [ 5 ] 　BOCCAL ET TI S , L A TORA V , MORENO Y , et al. Complex networks : st ruct ure and dynamics [ J ] . Phys Rep , 2006 , 424 : 175 308. [ 6 ] 　郭雷 , 许晓鸣. 复杂网络 [ M ] . 上海 : 上海科技教育出版社 , 2006. [ 7 ] 　WA T TS D J . Small worlds : The dynamics of networks be tween order and randomness [ M ] . Princeton : Princeton Uni versity Press ,1999. [ 8 ] 　汪小帆 ,李翔 ,陈关荣. 复杂网络理论及其应用[ M ] . 北京 :清华 大学出版社 ,2006. (责任编辑 :翁爱湘)